聚合物驅產油量預測模型的比較研究
丁顯峰
(西南石油大學理學院,四川 成都 610500)
邱海燕
(西南石油大學化學化工學院,四川 成都 610500)
聚合物驅產油量預測模型的比較研究
丁顯峰
(西南石油大學理學院,四川 成都 610500)
邱海燕
(西南石油大學化學化工學院,四川 成都 610500)
聚合物驅產油量預測結果的可靠性直接關系到油田開發年度規劃和中長期規劃的編制部署,因此預測模型的選擇尤為重要。介紹了聚合物驅產油量預測的5種模型:廣義翁氏模型、Weibull模型、瑞利模型、Logistic模型和HCZ模型。應用這5種模型分別對克拉瑪依油田七東區三采克下組聚驅產油量進行了預測,對比分析表明Weibull模型和Logistic模型對實際產油量擬合程度較其他3種模型高,預測結果誤差均在10%以內;各個模型考慮的因素不盡相同,在進行實際應用前應對這些模型擇優利用。
聚合物驅;產油量;預測模型
聚合物驅是油田繼水驅后廣泛采用的提高采收率技術。目前,研究常規聚合物驅產油量預測方法很多[1-4],不同的預測方法從不同的角度對各方面有用的信息進行挖掘整理,所利用的信息也是不相同的;同時,由于預測環境中不同影響因素的相互作用,真實過程可能會以人們預想不到的方式進行變化,針對某些因素所建立的預測模型就會面臨假設性錯誤的風險,因此,選擇合適的預測模型對聚驅產量的預測尤為重要。筆者通過分析5種預測模型的特點,比較了5種模型在聚合物驅中的預測效果,為選擇合適的預測模型提供依據。
1 預測模型
聚合物驅的有效期比水驅短,一般為2~5年,因此為保證預測模型取得較好的預測效果,將聚合物驅產油量預測的單位時間取為月。
1.1廣義翁氏模型
廣義翁氏模型[5]是1996年陳元千和胡建國在翁氏模型的基礎上,基于概率統計學中的伽馬分布進一步推導而得到的。該模型被廣泛應用在油氣田產量的預測之中,效果較好。具體表達式為:
Q=atbe-(t/c)
(1)
式中,a、b、c為3個模型參數;t=y-y0,t為生產時間,mon;y為預測的月份;y0為預測產量的起始月份;Q為某一生產時間的產量,t。
1.2Weibull模型
Weibull模型[6-7]即Weibull 1939年提出的統計分布模型,該模型的分布密度函數在隨機變量[0,+∞)區間內的積分為1,聚合物驅產油量與累積產油量的比值隨聚合物驅生產時間的變化具有相似特征,因此,聚合物驅的產油量可表示為:
(2)
式中,α、β為模型參數;NR為聚合物驅階段油田的可采儲量,t。
1.3瑞利模型
瑞利模型[8]也是基于數理統計中瑞利分布密度函數,在隨機變量[0,+∞)區間內的積分為1,與Weibull模型類似,聚合物驅的產油量可表示為:

(3)
令a=2NR/c,則有:
Q=ate-(t2/b)(a、b為模型參數)
(4)
1.4Logistic模型
Logistic模型[9-10]是一個屬于增長類型的模型,由美國Hubbert于1962年首次提出,又稱Hubbert模型。其表達形式為:

(5)
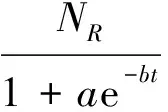
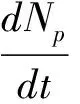
(6)
1.5HCZ模型
HCZ模型[11]是1995年由胡建國、陳元千和張盛宗基于累積產量隨時間遞增的信息特征,結合大量油氣田的統計研究成果,推導建立的預測模型。該模型可用于預測油氣田的產量、累積產量、可采儲量和最高年產量及其發生的時間,并能簡化為廣泛應用于經濟增長預測和資源增長預測的龔帕茲(Gompertz)預測模型。其具體表達式為:
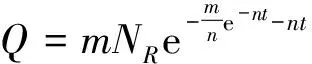
(7)
2 實例分析
克拉瑪依油田七東區三采克下組2006年9月開始注聚合物,聚合物驅含油面積1.25km2,有效厚度14.8m,地質儲量193.9×104t,總井數9口,采用200m井距五點法面積井網進行開采。利用七東區三采克下組的生產數據,對式(1)、(2)、(4)、(6)和(7)進行線性回歸分析,結果如下:
廣義翁氏模型:a=26.40,b=2,c=13.97,相關系數R=-0.9973。
Weibull模型:α=2.3,β=3760.95,NR=109656.2,相關系數R=-0.9944。
瑞利模型:a=155.7168,c=1705,相關系數R=-0.9750。
Logistic模型:a=708.74,b=0.02625,NR=121765.4,相關系數R=-0.9967。
HCZ預測模型:m=0.2150,n=0.0514,NR=135716.7,相關系數R=-0.9911。

圖1 實際產油量與預測產油量對比
各模型預測產油量與實際產油量見圖1。從圖1中可以看出,在產量初始上升階段各預測模型預測數值,廣義翁氏模型和Weibull模型預測誤差較大,其他3種模型誤差較小,基本沒有太大差異;在產量快速上升階段HCZ模型誤差最大,瑞利模型誤差次之,Weibull模型和Logistic模型預測數值的誤差最小;達到聚驅最大產量后,Weibull模型和Logistic模型預測值下降趨勢較其他3種模型大,瑞利模型和廣義翁氏模型下降趨勢較小,HCZ模型從整體上看只適合作為聚合物驅產油量初始上升和下降階段的預測;從整個預測數據與實際數據對比看,Weibull模型和Logistic模型預測比較準確,擬合程度較高。
表1為最后10個月的實際產量和各模型預測值誤差對比,通過實際值與預測值的比較可見, 除HCZ模型初始預測相對誤差較大外,誤差均在10%以內;比較而言Weibull模型和Logistic模型在整個聚合物驅生產過程中擬合程度高,預測結果誤差小,適合聚合物驅產量的預測。
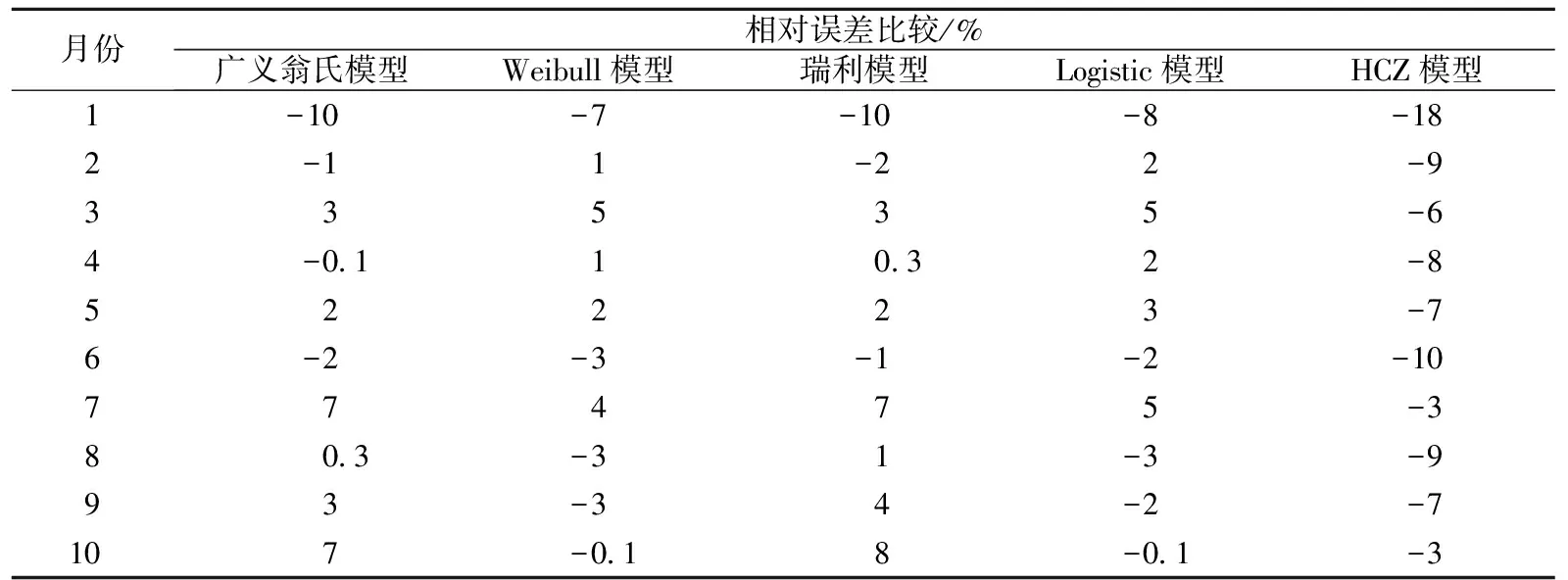
表1 實際產量和各模型預測值誤差對比
3 結 論
1)在整個聚驅產量預測過程中Weibull模型和Logistic模型更符合聚合物驅的實際生產動態,對油田聚驅產油量的預測結果更符合實際情況,誤差都低于10%;瑞利模型和廣義翁氏模型預測的結果精確程度稍差些;由于HCZ模型預測誤差較大,建議在克拉瑪依油田不使用該模型預測。
2)關于聚合物驅產油量預測模型很多,對于相同的實例,不同的預測模型結果是有差異的,各個模型考慮的因素也不盡相同。聚合物驅油的機理較為復雜,要建立準確的和普適的預測模型較為困難,只能說某一模型更適合于某一特定條件的油田,所以對于這些模型擇優利用,才能達到最優化設計的目的。
[1]劉朝霞,張禹坤,蔣平.Weibull與HCZ預測模型在聚合物驅產油量預測中的應用[J].油氣地質與采收率,2007,14(6):76-78.
[2]孫強,鄧兵,馬麗梅.廣義翁氏與瑞利模型在聚合物驅產量預測中的應用[J].大慶石油地質與開發,2003,22(5):58-59.
[3]黃學,劉朝霞,韓冬,等.一種預測聚合物驅開發動態的新模型[J].石油勘探與開發,2009,36(2):228-231.
[4]石成方,肖偉,王鳳蘭.聚合物驅油開發指標預測模型[J].石油學報,2005,26(5):78-80,84.
[5]陳元千,胡建國.對翁氏模型建立的回顧及新的推導[J].中國海上油氣地質,1996,10(5):317-324.
[6]陳元千.預測油氣田產量的Weibull模型[J].新疆石油地質,1995,16(3): 250-255.
[7]陳元千,趙慶飛.Weibull預測模型與乙型水驅曲線的聯解法[J].新疆石油地質,2000,21(5): 405-407.
[8]陳元千.瑞利模型的完善推導與應用[J].油氣地質與采收率,2004,11(4):39-41.
[9]陳元千,胡建國,張棟杰.Logistic模型的推導及自回歸方法[J].新疆石油地質,1996,17(2): 150-155.
[10]樂平,陳小凡,崔力公,等.產量研究中翁氏模型和Logistic模型的建議求解[J].石油天然氣學報(石油天然氣學報),2009,31(4): 277-279.
[11]胡建國,陳元千,張盛宗.預測油氣田產量的新模型[J].石油學報,1995,16(1):79-86.
[編輯] 洪云飛
10.3969/j.issn.1673-1409(N).2012.12.024
TE357
A
1673-1409(2012)12-N074-03

