對稱型混合雙公比車床主傳動系統設計與仿真*

鐘相強，梁利東

(安徽工程大學機械與汽車工程學院 先進數控和伺服驅動技術安徽省重點實驗室，安徽 蕪湖 241000）

0 引言

機床設計過程中，首先是概念設計和方案論證，然后進行產品設計和設計論證，通過周而復始的設計——實驗——設計過程，產品才能達到要求。在激烈的市場競爭環境下，基于實際物理樣機的設計驗證過程嚴重制約了產品的研發速度和產品質量，通過虛擬樣機技術，可以對機械系統進行運動和動力學仿真，在產品設計階段發現產品設計中的潛在問題。

齒輪嚙合傳動是機械傳動中應用最廣泛的運動和動力傳遞裝置，其力學行為和工作性能對整個機器有重要影響。利用NX和ADAMS建立齒輪嚙合虛擬樣機，對其進行動力學仿真，為機械傳動系統的動態特性優化提供理論指導。

1 車床主傳動系統的設計

1.1 參數確定

已知:nmax=1320r/min，nmin=42.5r/min，P=5.5KW，φ1=1.26，φ2=1.58轉速級數計算見式1。

由式1，可得 z1=16，z2=9，而 z=12。這樣使得設計的轉速在采用雙公比時有相應的級數空隙轉速。

1.2 運動設計

在通用機床上，每級轉數使用的機會不大相同，經常使用的轉速一般是在轉速范圍的中段，轉速范圍的高、低段使用較少，雙公比傳動就是針對這一情況而設計。主軸的轉速數列有兩個公比，轉速范圍中經常使用的中段采用小公比，不經常使用的高、低段用大公比。經調整后的結構式為:12=25×32×26，在高低段出現4個轉速空檔。

根據主變速傳動系統設計的一般原則:傳動副前多后少原則、傳動順序與擴大順序相一致的原則、變速組的降速要前慢后快和中間軸的轉速不宜超過電動機的轉速的原則，可知，傳動線要前密后疏，依次來安排各變速組的傳動順序［1-2］。最終繪制的轉速圖見圖1，按照主傳動轉速圖以及齒輪齒數繪制的主傳動系統圖見圖2。

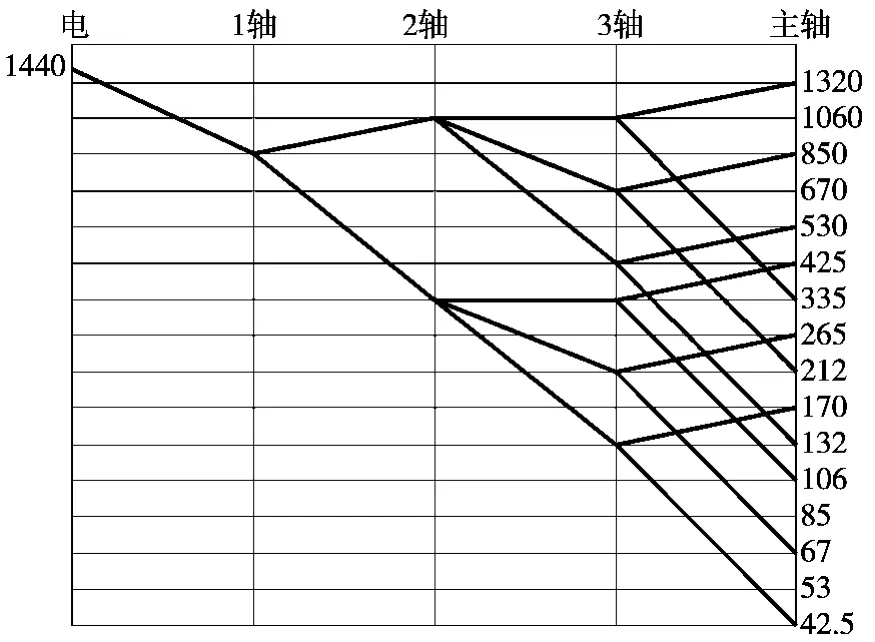
圖1 轉速圖

1.3 基于NX的主傳動系統TOP-DOWN虛擬樣機

建立整車總裝配模型為ASM_LATHE_12，在總裝配模型內分別建立四根傳動軸裝配體依次命名為:ASM_axis_1、ASM_axis_2、ASM_axis_3 和 ASM_axis_4。依次在每個傳動軸裝配體內，建立傳動軸模型。建立好空模型后，建立第一根傳動軸模型，以簡單的圓柱代替傳動軸，固定第一根傳動軸，之后每個傳動軸建立好后，約束在總裝模型的XY平面內，相對于上一根傳動軸按照設計好的距離，軸向方向適當即可。完成傳動軸的初步設計和安裝后，在傳動軸裝配體里依次調入做好的齒輪模型，并進行適當的安裝。

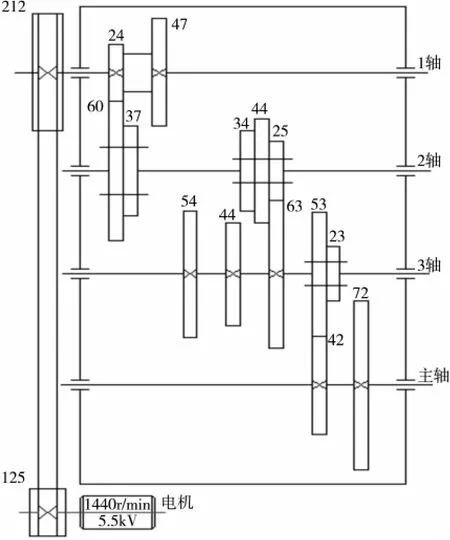
圖2 主傳動系統圖

設計過程中要對3D草圖進行不斷的調整，確保軸向和徑向尺寸不會過大，齒輪在軸上的排列合理，齒輪與齒輪、齒輪與軸間不會相互干涉等，齒輪最小壁厚不至過小等。最終主傳動系統3D圖見圖3。

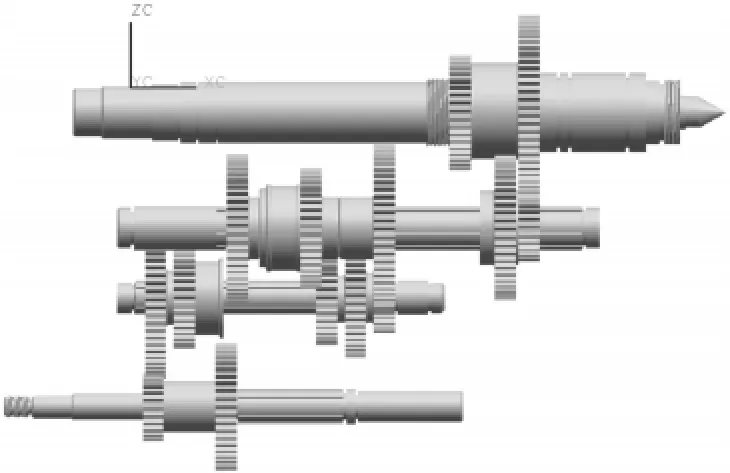
圖3 主傳動系統3D圖

2 基于ADAMS的齒輪嚙合動力學分析

2.1 齒輪嚙合虛擬樣機

把NX中兩齒輪嚙合的文件另存為x_t格式，導入到ADAMS中。在仿真分析時齒輪變形很小，視為剛體。其動力學性能除了受接觸變形的影響外，還受到制造誤差、嚙合間隙等的影響。為便于分析，對齒輪機構的剛體模型做如下假設:裝配間隙為零，制造誤差忽略不計;假設轉動約束為理想約束;各部件均視為剛體;暫不考慮齒輪嚙合變形對動力學性能的影響。

根據齒輪傳動的運動規律，系統加入的約束和載荷為:在主動輪和被動輪上分別施加旋轉副，機架為地。在齒輪對之間施加實體-實體碰撞力，以仿真齒輪嚙合傳動;在輸入軸的轉動副處施加恒定的轉速驅動;在輸出軸上加一個恒定負載轉矩，模擬工作機負載。［3-5］

2.2 基于ADAMS的接觸碰撞算法

在ADAMS中有兩類接觸力:一類是基于Impact函數的接觸力，另一類是基于Restitution函數的接觸力。Impact是用剛度系數和阻尼系數來計算碰撞力，而Restitution是用恢復系數來計算碰撞力。該齒輪嚙合虛擬樣機用Impact函數來計算接觸力。

Impact函數的表達式見式2。

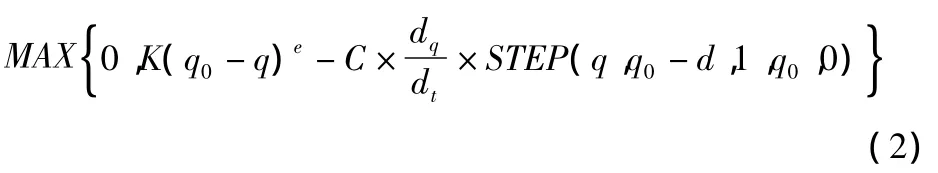
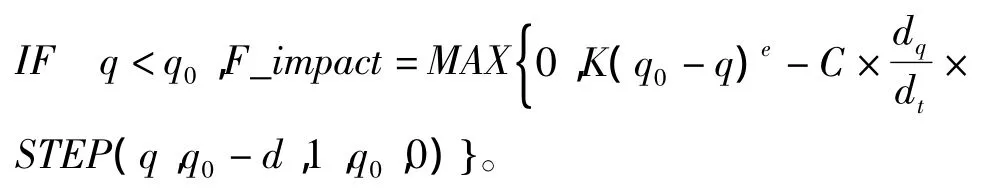
輪齒碰撞所引起的沖擊力，可以作為兩個變曲率半徑柱體撞擊問題。根據Hertz碰撞理論，考慮接觸面積為圓形時，可得撞擊時接觸法向力P和變形δ關系見式3。

k取決于撞擊物體材料和結構形狀，見式4。

由于兩齒輪材料均為45#鋼，其泊松比v1=v2=0.29，彈性模量 E1=E2=2.07 ×105N/mm2，把數據帶入得 E=1.13 ×105N/mm2，R=22.436N/mm2。由于齒輪的齒高和分度圓半徑相比較小，可近似以分度圓半徑代替齒輪接觸點的當量半徑，則齒輪的剛度系數k=8.396×105N/mm2。根據經驗值，碰撞指數e取2.2，阻尼系數c取100N·S-1/mm，嵌入深度d取0.1mm。考慮碰撞時摩擦，兩齒輪都按潤滑處理，取動摩擦系數為0.05，靜摩擦系數為0.08［6-7］。

2.3 齒輪嚙合動力學仿真和結果分析

基于該虛擬樣機模型，在主動輪上加恒轉速驅動4800deg/sec(800r/min）。從動輪施加一個恒負載轉矩101300N·min，為了使施加的負載不出現突變，使用STEP函數使負載在0.2s內平緩施加，即STEP(time，0，0，0.2，101300）(time 為時間自變量）。由STEP函數施加的負載轉矩如圖4所示。

圖4 負載轉矩

主動輪、從動輪的轉速ω隨時間t變化曲線見圖5和圖6。各齒輪軸線與ADAMS中坐標系統Z向平行，設逆時針為轉動的正方向。

圖5 主動輪轉速隨時間變化曲線

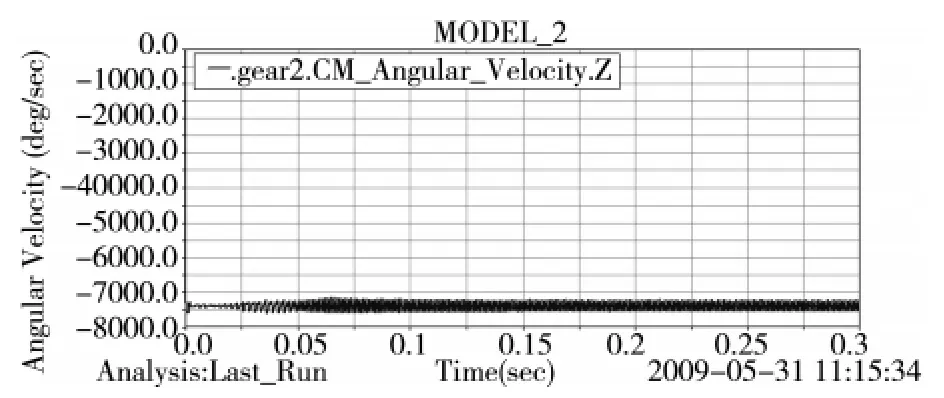
圖6 從動輪轉速隨時間變化曲線

從轉速方向上分析:圖5轉速為正號，表示主動輪轉速方向為逆時針;圖6轉速值為負號，表示從動輪轉速方向為順時針。而該對齒輪為外嚙合齒輪，說明各齒輪轉向滿足外齒輪嚙合傳動關系。

從轉速大小上分析:在虛擬樣機啟動瞬間，有一個較大沖擊，表現為從動輪的轉速有個從零到負的突變。后面的運行中轉速恒定，平穩運行，主動輪轉速為給定的 4800deg/sec，從動輪轉速平均值為7626.52deg/sec(1271.09r/min），并在一定范圍內周期性波動，這是由于齒輪傳動過程中的振動和沖擊引起的。

轉速和傳動比的理論計算值及仿真值見表1。其中，仿真值按0到0.3s輸入轉速恒定階段從動輪轉速的平均值選取，相對誤差λ=|仿真值-理論計算值|/理論計算值。

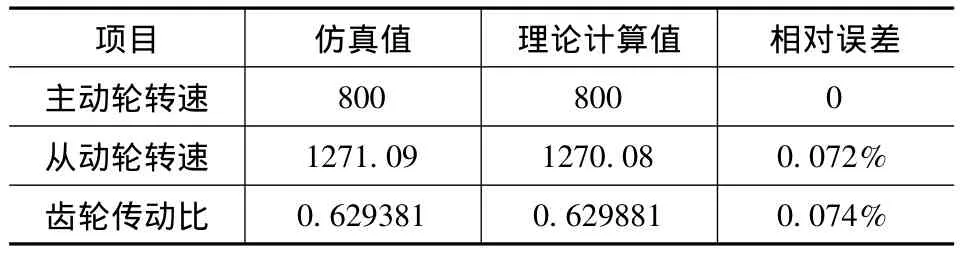
表1 轉速和傳動比仿真值與理論計算值比較

由表1可知，各齒輪轉速仿真和理論值基本一致，仿真得到的傳動比值和理論計算值也相當接近，說明該齒輪嚙合虛擬樣機滿足傳動比要求，仿真方法具有一定的現實指導意義。

齒輪的嚙合力仿真曲線見圖7，圖中上部曲線為嚙合力時域圖，下部曲線為嚙合力頻域圖，即嚙合力F隨頻率f變化曲線。

圖7 齒輪嚙合力時域及頻域圖

從時間歷程上分析:在轉速啟動瞬間，有一個很大的沖擊，表現為各級嚙合力有一個很大的值，0s到0.2s之間，為加速階段，隨著速度的增加，嚙合力的波動幅度增加，波動周期減小。在0.2s以后，為恒定轉速階段，嚙合力在一個均值(即齒輪傳動中的靜載荷）都表現為一個穩定的值，體現了輪齒周期性嚙入嚙出的特點。

從頻域上分析:從齒輪嚙合力頻域圖來看，齒嚙合力在759.4Hz點幅值最大，即嚙合頻率為759.4Hz。由齒輪嚙合頻率理論計算得知 fZ=760Hz，可見，齒輪嚙合頻率的仿真值和理論值較吻合，從頻域上說明了仿真的可信度。

3 結束語

基于NX自頂向下方法構建了對稱型混合雙公比車床主傳動系統三維模型，基于Hertz接觸動力學理論，在ADAMS中建立了齒輪傳動系統動力學特性的仿真模型，計算出齒輪嚙合的轉速、嚙合力等曲線數據，與理論計算結果非常接近，對于改善機械傳動系統動力學性能和關鍵零部件設計起到重要的指導作用。

［1］馮辛安.機械制造裝備設計(第2版）［M］.北京:機械工業出版社，2005.

［2］金怡果，袁國文.基于灰色聚類的機床主傳動非常規變速系統的優化設計——對稱型混合公比的傳動系統［J］.組合機床與自動化加工技術，2007(4）:28-33.

［3］于恩明.機床傳動系統虛擬樣機仿真技術的研究［D］.長春:長春理工大學，2005.

［4］賈麗剛，張宇，郭勤靜，等.CAD/CAM一體化技術在車床主傳動系統設計上的應用與研究［J］. 機床與液壓，2007，35(10）:91-93.

［5］李新勇，王華棟.基于虛擬樣機技術的折剪兩用機床主機建模與仿真［J］.制造技術與機床，2008(8）:44-47.

［6］高清冉，孫海燕，李海洪，等.基于虛擬樣機的機床設計與仿真研究［J］. 機械設計，2009，26(7）:16-19.

［7］袁文武，蔡慧林，任剛.基于UG和ADAMS的齒輪嚙合動力學仿真［J］. 煤礦機械，2010，31(2）:40-43.