地鐵列車牽引計算的研究

林 青

（西南交通大學 信息科學與技術學院，成都 610031）

城市軌道交通是城市公共交通客運系統的骨干，是以大眾化、大運量、大站距為特點的安全、舒適、快速、準時的綠色交通工具，是采用獨立的專用軌道、高密度運行的、為中長運距服務的、現代化的城市客運快速骨干系統，通常是指服務于城市內部為主和適當外延的線路。對城市軌道交通車輛運行過程進行實時仿真模擬可以更好地滿足運輸需求。準確、快速地計算出列車在各種不同條件下的運行效果并予以評價是牽引計算的任務。

1 城市軌道交通的特點

城市軌道交通與大鐵路在諸多方面有很大不同，主要表現在：緊急制動距離很短；區間長度比較短，類似公共汽車的站間距；在運行中存在頻繁的啟動和制動過程；線路條件苛刻，曲線半徑有時甚至小于250 m，坡度有時很大（很小），甚至超過4 %；操縱要求非常嚴格，啟動和制動過程要求快速、平穩，停站要求非常準確，舒適度要求較高等。

2 CBTC安全制動模型

IEEE1474.1關于CBTC系統推薦的典型的安全制動模型如圖1。

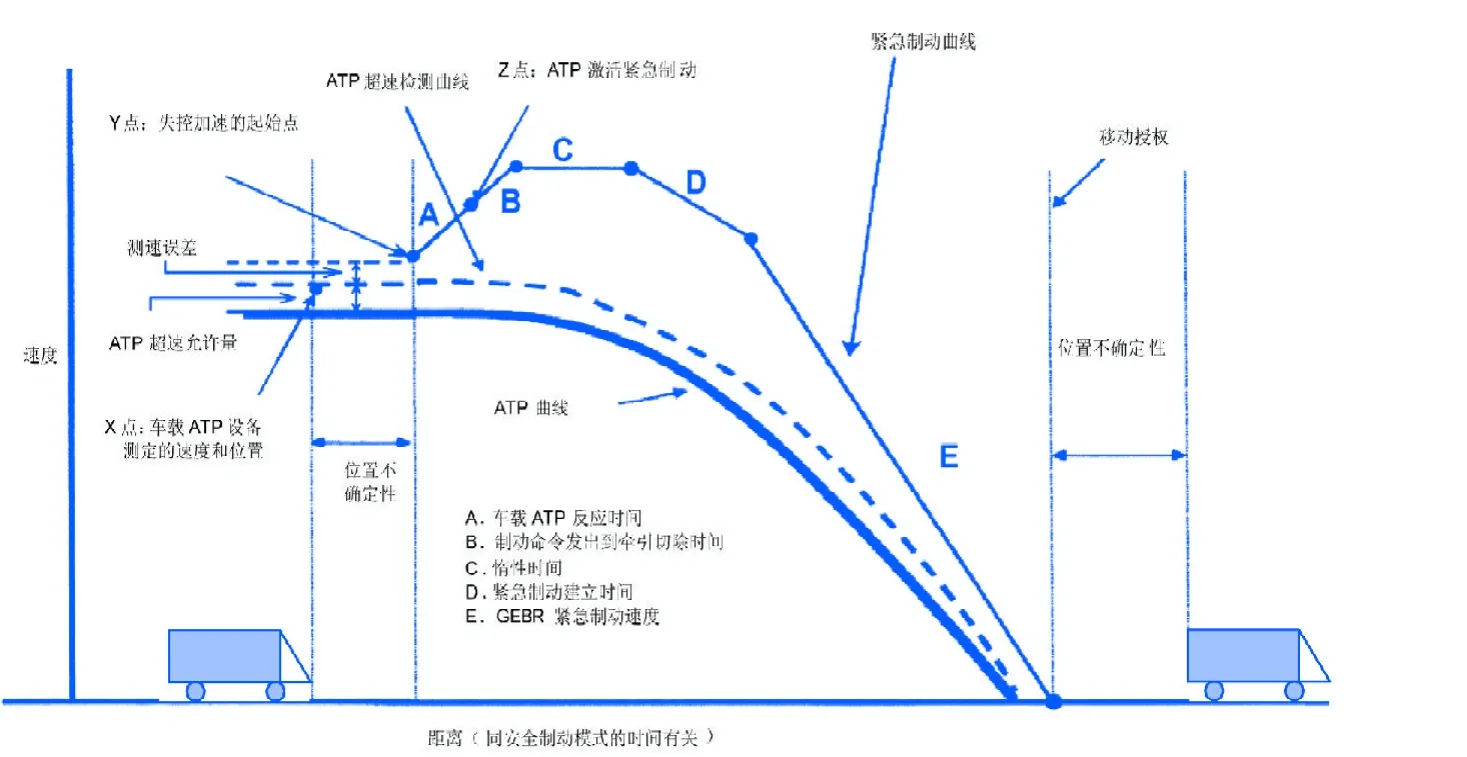
圖1 CBTC系統安全制動模型

圖中緊急制動曲線表示的是在最不利情況下的開環速度-距離曲線。一旦施加緊急制動，列車將遵循該曲線運行制動列車停止。緊急制動曲線必須保持等于或小于安全速度曲線，若超過安全速度曲線，就會出現嚴重的危險（脫軌或撞車）。

圖中的ATP超速檢測曲線就是本文以后將會提到的緊急制動觸發曲線，指如果ATP子系統一旦發現列車在某檢測點的測量速度超過該曲線，就會立即觸發緊急制動程序的速度-距離曲線。激活緊急制動后，ATP子系統就脫離原來的控制，列車按照（或者低于）緊急制動曲線進行緊急制動。緊急制動曲線包括一個失控牽引階段，這個階段直到牽引完全取消為止。ATP曲線是指低于ATP超速檢測曲線一個超速容限的速度-距離曲線。它是ATP子系統所使用的基本曲線。

3 建模

本文在上述IEEE1474.1關于CBTC系統推薦的典型的安全制動模型的基礎上，建立了如下的列車制動模型，如圖2。

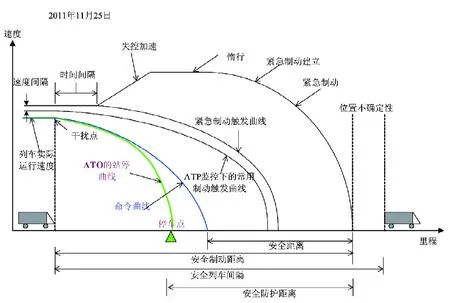
圖2 列車制動模型

列車制動模型的計算：EB包絡線的計算，緊急制動觸發曲線（EB觸發曲線）的計算，全常用制動觸發曲線（FSB曲線）的計算，列車命令速度曲線的計算，實際運行速度曲線的計算。

4 牽引計算

4.1 EB包絡線的計算

根據IEEE1474.1標準安全制動模型繪制的列車制動模型，EB包絡線由列車失控加速曲線、列車惰行曲線、列車緊急制動曲線構成。

EB包絡線中列車失控加速曲線是列車制動時，由于某些原因，列車沒有制動反而以更大的加速度前沖的過程。失控加速完成時，列車的速度達到最大值。按列車運行方向計算時，列車的失控加速度按列車失控加速前的速度來選取；按列車運行反方向計算時，列車的失控加速度按列車失控加速后的速度來選取，且取為反向的失控加速度。

EB包絡線中列車惰行曲線是列車停止失控加速到開始制動的過程，列車保持一段時間的惰行狀態，惰行完成后，列車進入緊急制動狀態。按列車運行方向計算時，列車的惰行加速度按列車惰行前的速度來選取；按列車運行反方向計算時，列車的惰行加速度按列車惰行后的速度來選取，且取為反向的惰行加速度。

EB包絡線中列車緊急制動曲線：列車在失控加速、惰行后進入緊急制動狀態，直到列車完全停止運行。列車的緊急制動減速度由用戶設定。

EB包絡線的繪制通常采用反向繪制的方法。EB包絡線的反向繪制是由安全停車點開始，倒推列車的緊急制動曲線，惰行曲線，失控加速曲線，是一次繪制而成的。安全停車點可以由用戶設定。

4.2 EB觸發曲線的計算

EB觸發曲線的計算是在包絡線計算的基礎之上進行的，必須先進行包絡線的計算，才能進行EB觸發曲線的計算。

EB觸發曲線與包絡線的關系：EB觸發曲線是由EB包絡線反向推導而成，EB包絡線的離散化后的（V-S）點通過列車惰行、失控加速的反向運算，推出EB觸發曲線的離散化（V-S）點，然后連續化成為列車的EB觸發曲線。

EB包絡線的離散化：EB包絡線是一條連續的曲線，為了計算EB觸發曲線，必須將其離散化，本系統采用位移的離散化，離散的間隔由用戶設置，一般取為10 cm～100 cm。

EB包絡線離散點推EB觸發曲線離散點：從EB包絡線離散點推導出惰行前的（V-S）點，簡稱中間點。從中間點推導出失控加速前的（V-S）點，此即EB觸發曲線離散點。

4.3 FSB觸發曲線的計算

FSB觸發曲線（列車常用全制動觸發曲線）又稱ATP Supervised Service Brake Profile（ATP監控的常用制動曲線），FSB觸發曲線由EB觸發曲線推導。

FSB觸發曲線的性質：全常用制動速度是非安全監控速度曲線，當列車速度觸及常用制動觸發曲線時，車載控制器將施加全常用制動；列車速度系統引用全常用制動觸發速度的目的是為了提高系統的可用性，避免系統頻繁發生緊急制動；與緊急制動的區別是當列車速度降低到正常范圍之內后，全常用制動的制動命令解除，列車無需完全停止。

FSB觸發曲線與EB觸發曲線的間隔為當前速度下的時間間隔Teb-fsb和速度間隔Veb-fsb；本系統中Teb-fsb和Veb-fsb均為用戶可設，Teb-fsb默認值為3.0 s，Veb-fsb默認值為2.5 km/h。

FSB觸發曲線的計算步驟：

（1）對EB觸發曲線實行離散化，本系統采用位移的離散化，離散的間隔由用戶設置，一般取為10 cm～100 cm；

（2）取緊急制動觸發曲線上的離散點（Xeb,Veb）；

（3）計算當前速度下的FSB觸發點位置：

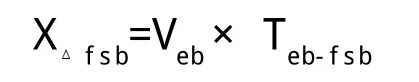
（4）計算全常用制動觸發點速度：

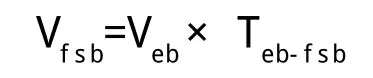
（5）得到對應的FSB觸發點：(Xfsb,Vfsb)

當緊急制動觸發曲線用函數表達：

Vebtrigger=f(s)

全常用制動觸發曲線可用函數表示為：

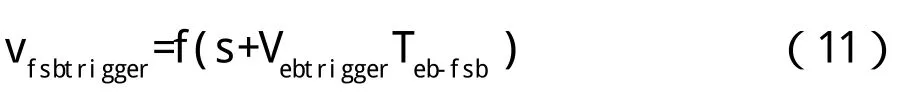
為了保證全常用制動觸發曲線上的任何一點的瞬時制動率都小于全常用制動率，用Teb-fsb（s）替代公式（11）中的Teb-fsb，并且：

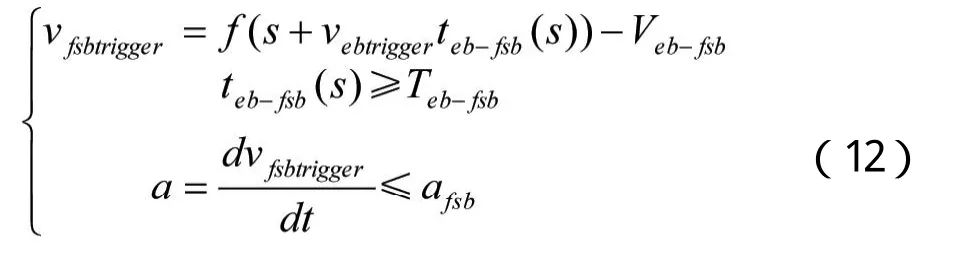
其中afsb為全常用制動率。

4.4 命令曲線的計算

基于同樣的算法，命令速度曲線與全常用制動觸發曲線的間隔為當前速度下的時間間隔Tfsb-ato和速度間隔Vfsb-ato，本系統中取Tfsb-ato為3.0 s，Vfsb-ato為2.5 km/h。

上式描述了列車采用ATO可變制動率點的停車方式（ATO variable brake rate），但列車在功能停車點（車站停車點或折返停車點）停車時，命令速度采用恒定制動率：

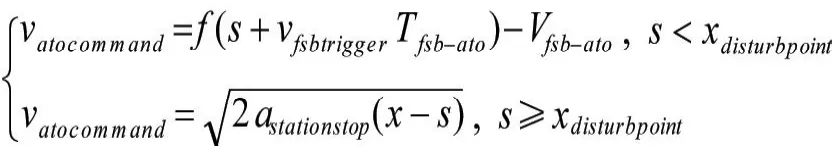
其中，x為車站停車點，astationstop為列車停站的恒定制動率，xdisturbpoint為停站初始點，即列車開始按照恒定的停站制動率進站停車的位置。

4.5 實際速度曲線

列車按照命令速度曲線行駛，形成列車實際速度曲線。與命令速度曲線基于同樣的算法。

4.6 仿真結果

以成都地鐵1號線為例，對該模型進行仿真驗證，得到的結果如圖3。

圖3 成都地鐵1號線仿真結果

5 結束語

列車的牽引計算過程是一個很復雜的過程，這是由于在實際運行過程中可以有不同的機車、不同的牽引曲線、不同的線路坡度組合。因此，本文根據一定的牽引原則，利用計算機對列車的牽引計算進行了模擬研究，較好地實現了在整個列車運行過程中牽引過程的模擬。

[1]謝小淞. 城市軌道交通列車牽引計算系統的研究[J]. 交通運輸工程學報. 2005，5（4）：20-26.

[2]鈕澤全. 牽引計算學[M]. 北京：中國鐵道出版社，1984.