基于B樣條的高頻比動平衡機的永久標定實現

趙鼎鼎 蔡 萍

上海交通大學，上海， 200240

0 引言

系統標定是動不平衡測試系統中的一項重要內容，用于確定測量傳感器輸出與不平衡量測量結果之間的對應關系。系統標定結果的優劣直接影響到不平衡量的測量精度，合理和優化的標定操作不僅能夠提高不平衡量的測量精度，同時也能夠提高系統的測量效率，降低工業現場操作的難度。

動不平衡測試系統與一般的測試系統有許多共同點，同時也有許多不同點。被測量轉子的強介入性和無法完全避免的校正平面之間的干擾性，都限制了動不平衡測量精度的提高。在硬支承平衡下，轉子本身的慣性力和系統阻尼都被忽略，而將系統按照靜力學的平衡法則進行動不平衡測量系統的標定和平面分離解算。這種忽略了轉子慣性力和系統阻尼的平面分離原理限制了動不平衡測試精度的提高。而且，轉子的慣性力和系統阻尼都會隨著測量轉速的改變而變化，所以單一測量轉速下的系統標定結果不能很好地滿足不同測量轉速下的動平衡測量要求。

長久以來一直認為測量轉速高于0.5倍系統固有頻率的平衡機是無法實現系統的永久標定的。在有關動平衡機的教材中，都將平衡機分作硬支承和軟支承來分別講解。為了實現系統的永久標定，不得不舍棄高轉速下軟支承平衡機測量精度高的優點。劉釗等[1]給出了試重法實現永久標定的原理。賀大拙[2]指出，轉子的慣性力和慣性力矩是導致永久標定和系統特性有差異的主要原因。周仕炎等[3]明確指出，系統的阻尼會導致永久標定方法的性能衰退和惡化，同時給出了一種相移電路用以補償系統阻尼對測量系統帶來的影響。劉健等[4]綜合了各種永久標定和狀態標定的方法，同時對各種標定方法進行了分析和比較，總結了各標定方法的優缺點。上述研究都只是分析了永久標定的問題所在，仍然限定于測量轉速小于0.3倍系統固有頻率這一前提，沒有給出一種通用的動平衡機的永久標定方法。

1 動不平衡測量過程

圖1對通用動不平衡測量過程進行了描述。不平衡轉子中存在著不對稱的質量微元，當轉子沿其幾何軸線旋轉時不平衡量表現為轉子旋轉時的離心力，同時激起支承系統的振動，其力學過程為轉子在不平衡量引起的離心力的作用下做受迫振動。依靠振動傳感器將支承系統的振動拾取出來，通過信號調理和信號處理電路模塊除去傳感器信號中與旋轉頻率不同的信號分量，提取得到不平衡信號的特征參數——與轉頻同頻信號成分的幅值和相位。最后再按照下面公式描述的動不平衡測量的平面分離方程分離出對應校正面上的幅值和相位：

f(Mω2)g(Cω)(Sη(1)η(2)…η(n))m=U

(1)

式中，ω為測量轉速；M為轉子的質量；C為系統的黏性阻尼系數；S為校正平面和傳感器平面之間的耦合；η為各種信號調理和信號處理環節的傳遞函數；m為校正面上的不平衡量；U為傳感器的輸出；f函數表示轉子慣性力對振動響應的影響；g函數表示黏性阻尼對振動響應的影響。

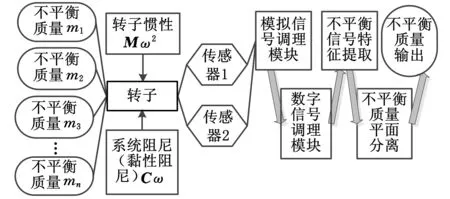
圖1 動不平衡測量流程

典型的動平衡測量的結構見圖2，轉子在彈性支承下沿軸線做旋轉運動，由達朗伯原理可以獲得系統的動力學方程：

(2)

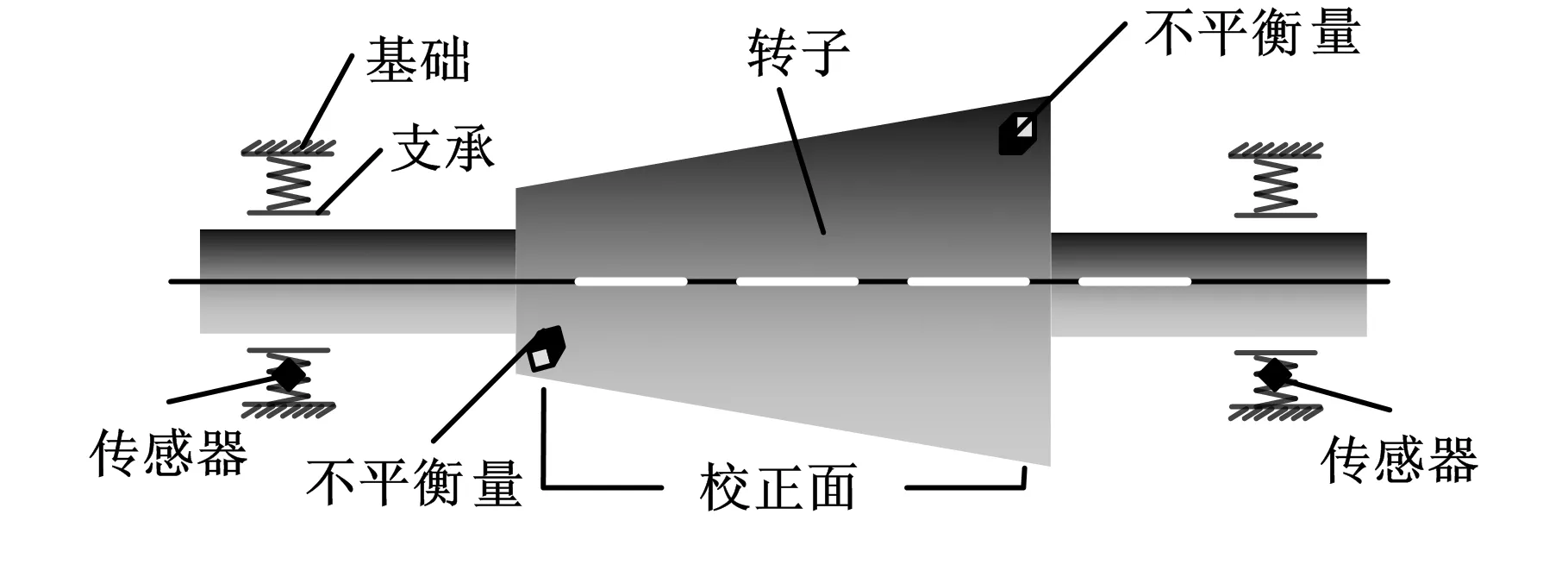
圖2 不平衡轉子測量示意圖

在系統的動力學方程(式(2))中，存在著與測量轉速密切相關的物理量，如轉子的慣性量Mω2和系統阻尼Cω。由于它們都是測量轉速的函數，所以無法直接實現與轉速無關的系統的永久標定。本文提出了改進的系統標定方法，該方法能夠克服測量轉速和轉子質量對測量系統帶來的影響，其標定的結果能夠涵蓋除轉子本身結構參數以外的所有系統參數對測量結果帶來的影響，從而能夠實現只需一次永久的標定即可在不同轉速下進行動平衡測量。

2 動平衡測量的標定過程

動不平衡測量的力學模型如圖3所示。圖3可以同時表示硬支承和軟支承的動不平衡測量系統力學模型。當被測量轉子繞X軸旋轉時，由于不平衡量的存在，轉子在旋轉的同時伴有沿Y軸的橫向平動和繞Z軸的擺動。平面A和平面B是按照校正工藝選取的校正平面，m1、m2是將分散的不平衡量等效集中到校正平面上的不平衡量。可以得出系統的動力學方程為[5]

(3)

式中，M、J為轉子質量和轉子繞Z軸的轉動慣量；C1、C2分別為兩個支承處的系統黏滯阻尼系數；K1、K2分別為支承處沿Y軸方向的剛度系數；y為轉子質心沿Y軸的平動位移；y1、y2分別為一維傳感器感受到的振動位移量；r1、r2為校正平面上的集中不平衡量所處徑向位置；θ為校正面上等效集中不平衡量位置之間夾角；l1、l2為兩個傳感器分別到轉子質心的距離；h1、h2為兩校正平面分別到轉子質心的距離。

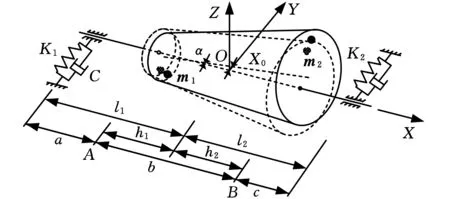
圖3 不平衡轉子的動力學模型

通過不平衡轉子的動力學方程(式(3))可以獲得動不平衡測量系統的系統標定方程：

(4)

式中，a、b、c為轉子的結構參數；m1、m2為校正平面上的不平衡質量；U1、U2為傳感器信號輸出。

標定系數ρ11、ρ21、ρ12、ρ22包含了不平衡量與測試結果之間除了轉子幾何參數以外的耦合關系，即標定的結果涵蓋轉子質量、系統阻尼、傳感器靈敏度和電路靈敏度在測量過程中的作用。解式(4)后可以獲得標定結果：

(5)

由于系統阻尼和轉子的慣性量是與測量轉速有關的函數，所以只有在標定轉速和測量轉速完全一致的情況下才會測量出比較精確的結果。為了實現整個轉速范圍內的準確測量，避免對測量結果進行補償和修正，需要對標定過程進行改進。首先，在測量的整個轉速范圍內選取能夠覆蓋整個測量范圍的有限個測量轉速，同時在平衡機允許的工件質量范圍內選取多個不同質量的轉子。然后分別在不同的測量轉速下采用不同質量的轉子對系統進行標定，獲得一組沿測量轉速和轉子質量分布的系統標定結果。最后，對得到的一組系統標定結果采用雙3次B樣條進行插值運算，獲得整個測量范圍內對應不同轉速和不同轉子質量的標定結果，以實現硬支承和軟支承下剛性轉子的動不平衡測量系統的永久標定。

3 多維網格插值原理

式(5)中動不平衡測量系統的標定結果與測量轉速和轉子質量密切相關，所以只在某個轉速和某個轉子質量下進行標定，尤其在軟支承下的動不平衡測量中(轉子質量和系統阻尼不可被忽略時)，是無法實現整個測量范圍內的系統的永久標定的。所以我們提出在有限個測量轉速和有限個不同轉子質量下對系統進行標定，在由測量轉速和轉子質量張成的網格上對標定結果進行插值以獲取整個測量范圍內的系統特性，實現系統的永久標定。B樣條有足夠的精度且可在計算機上方便地實現，適用于做插值以獲取系統的永久標定結果。

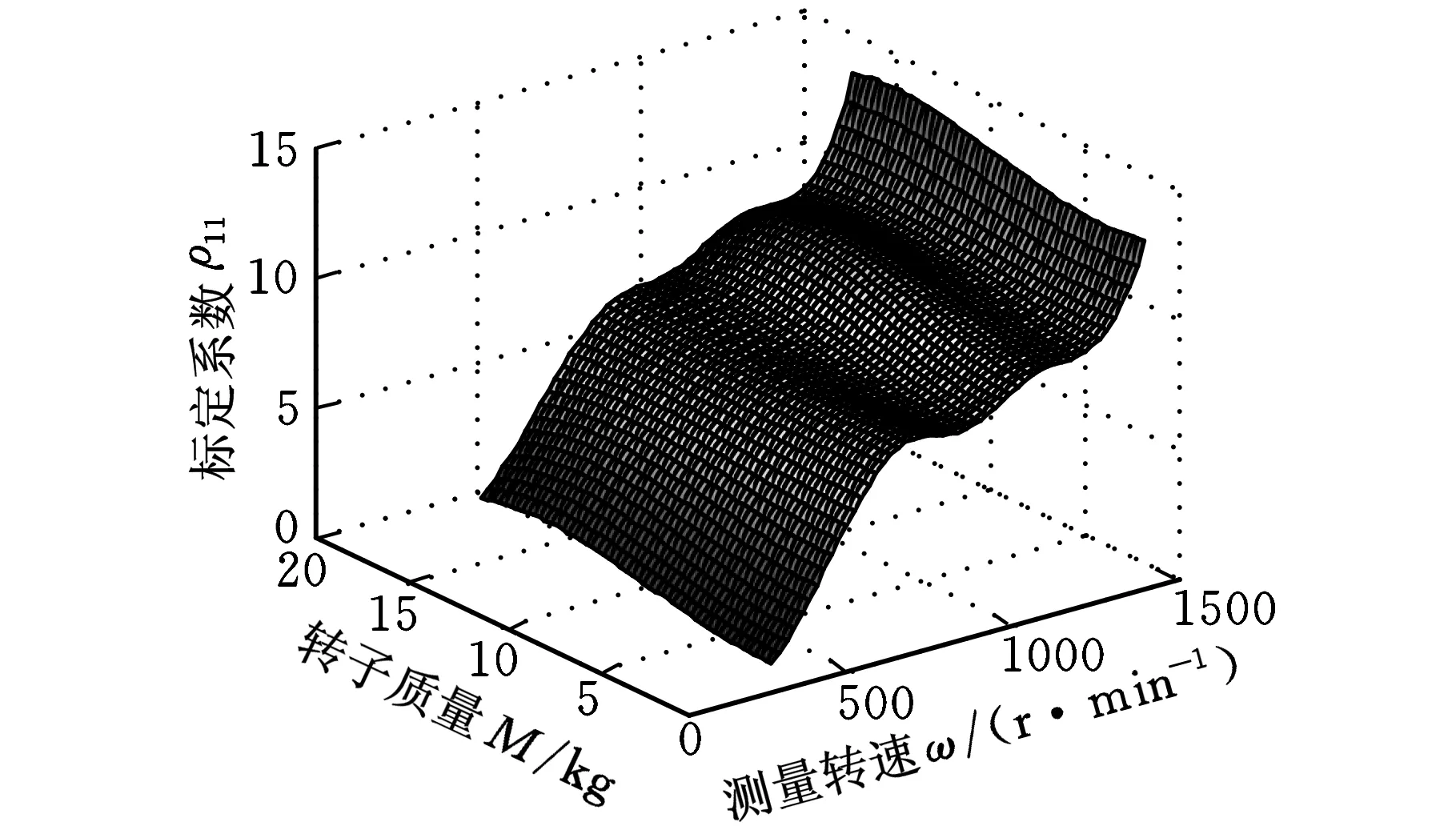
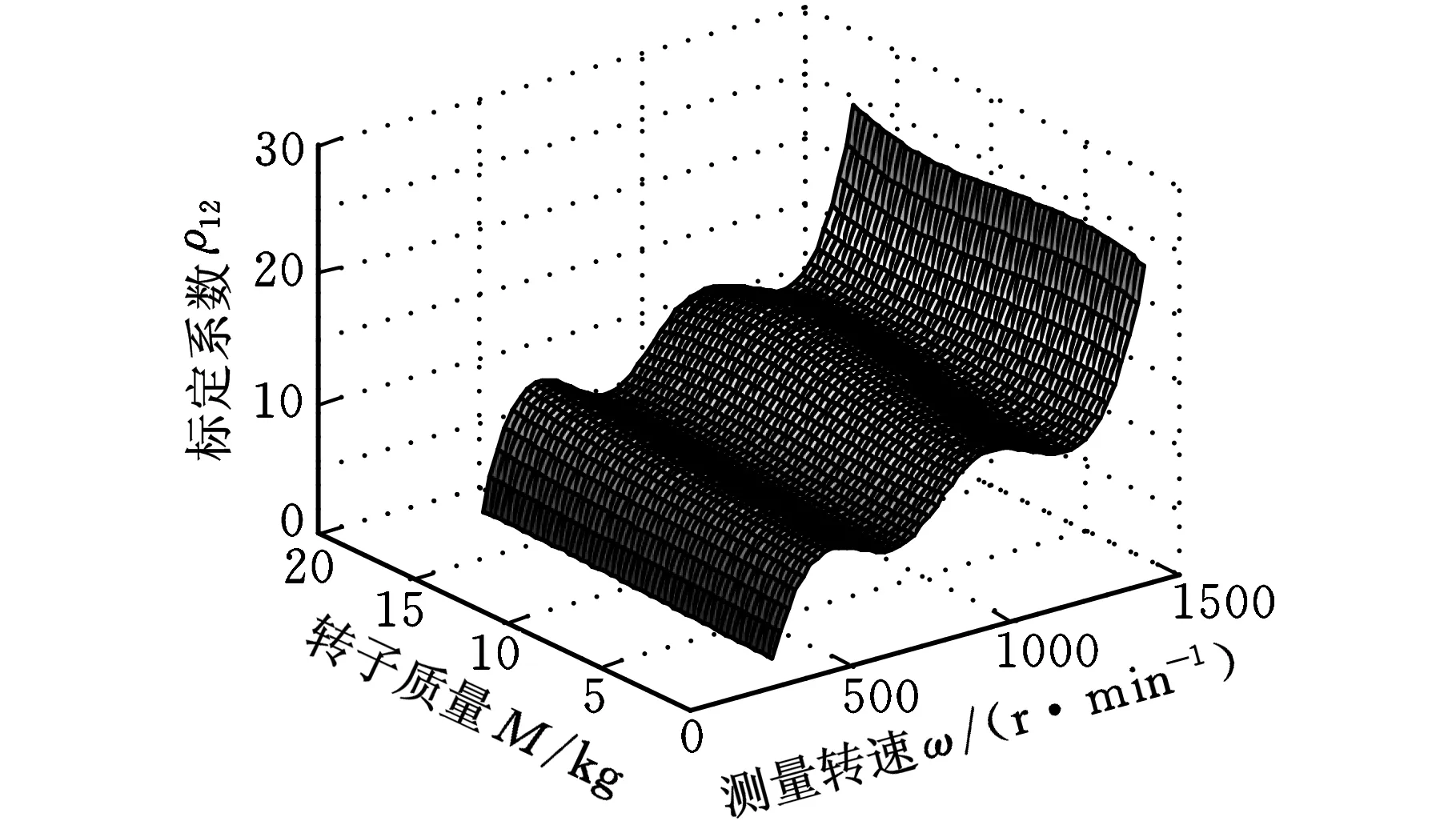
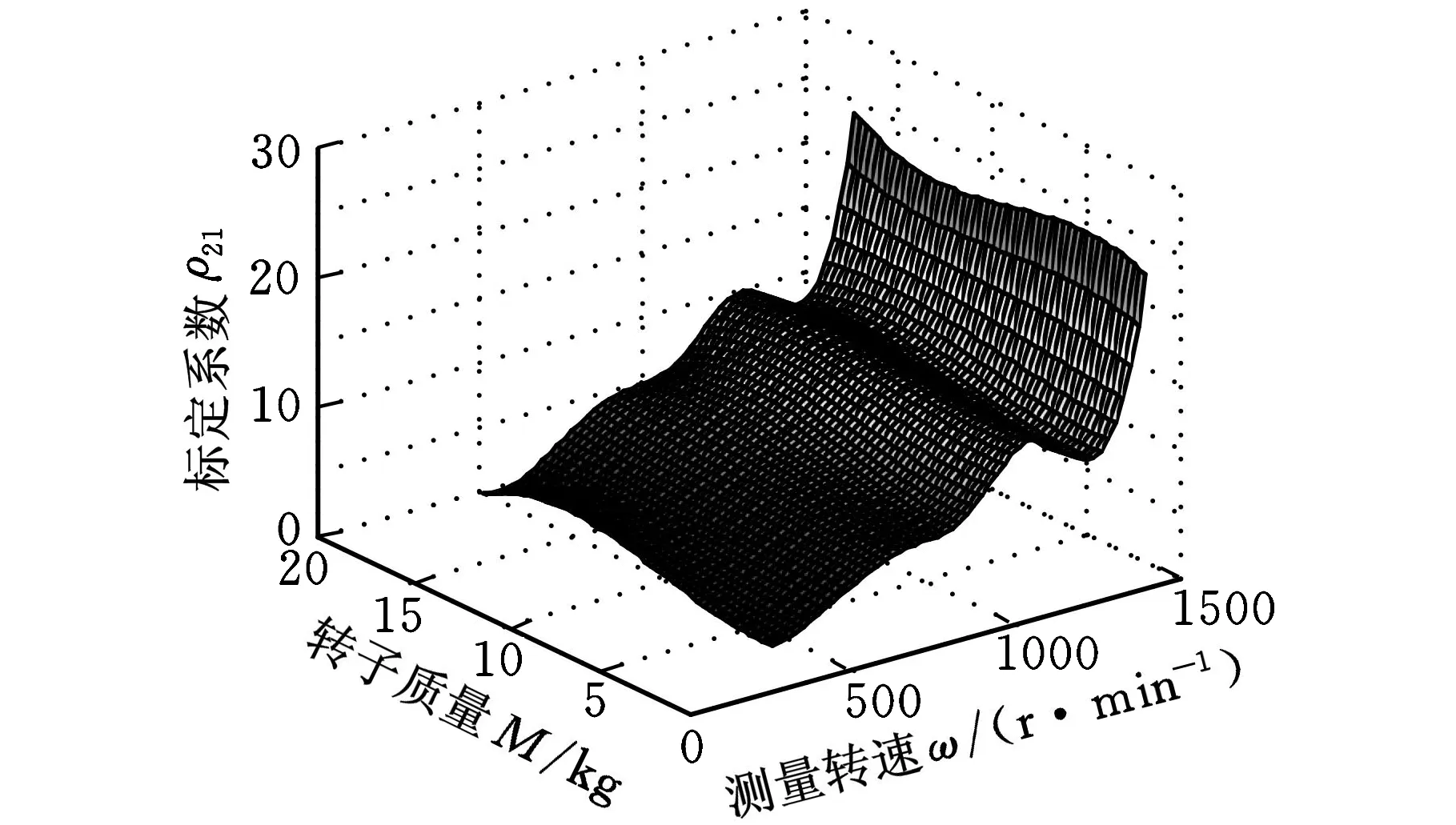
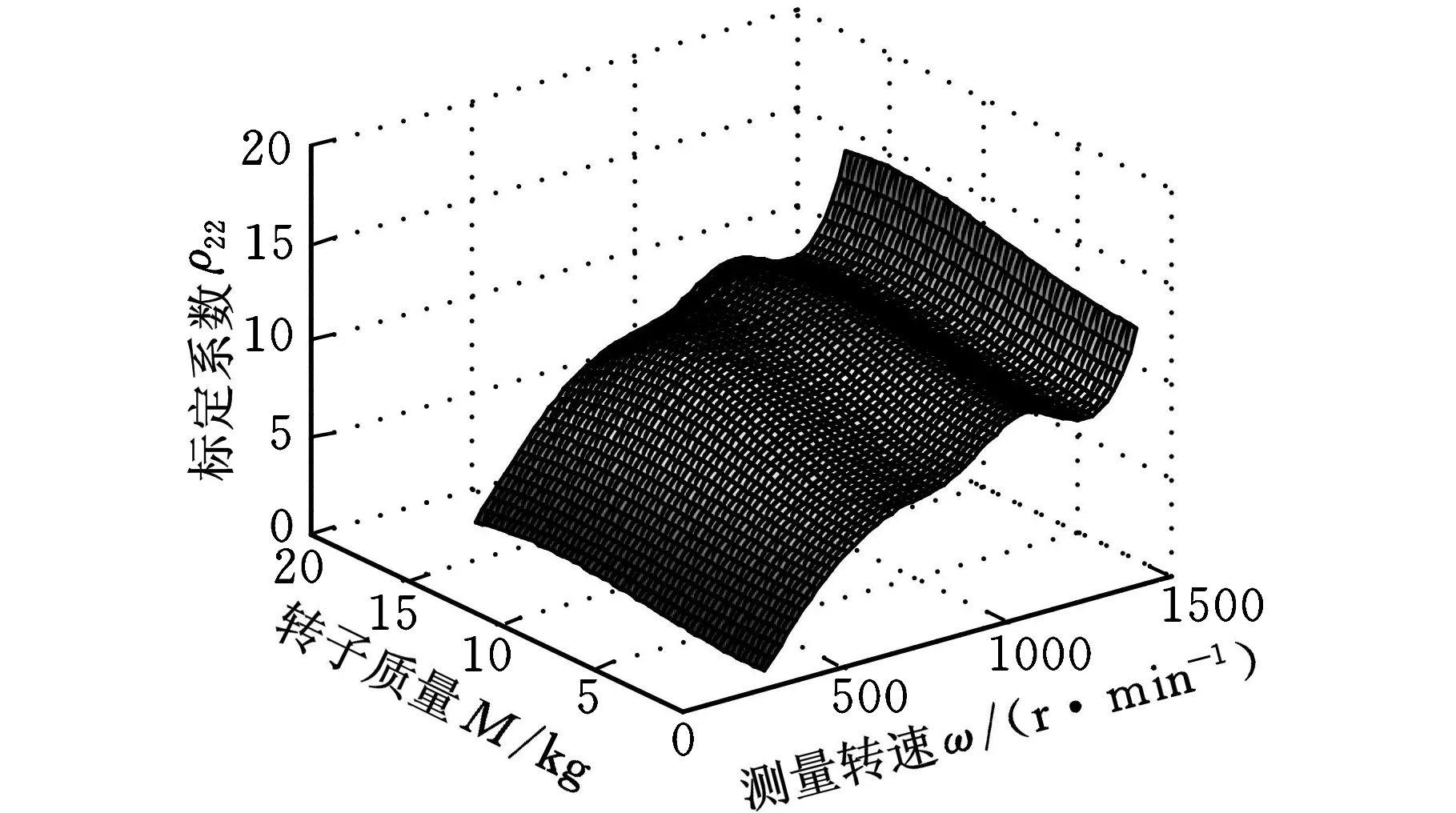
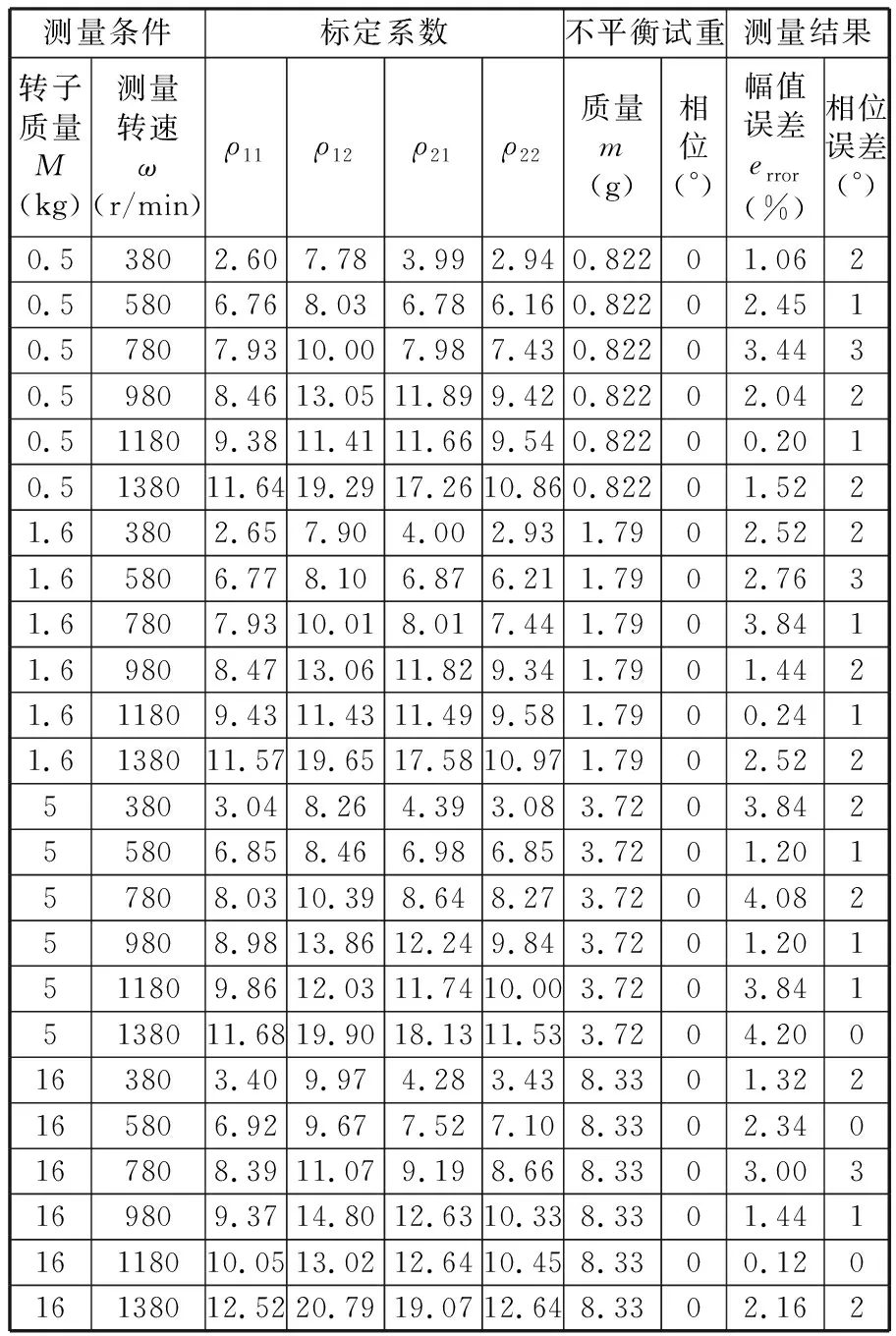
在整個測量范圍內，引入分劃Δ=ΔωΔA，其中，Δω是對測量轉速的分劃，ΔA是對不同轉子質量的分劃，定義Δω∶α=ω0<ω1<…<ωL=β;ΔA∶a=A0

B樣條插值張成的曲面可表示為

(6)

ωk≤ω≤ωL+1,Ak≤A≤AN+1

其中，pi,j為節點(ω,A)上的控制點；Gi,k(ω)、Gj,k(A)分別為沿分劃Δω和沿分劃ΔA上的k次基函數，并且有如下的迭代形式(Cox-de Boor)[6-7]：

(7)

在式(7)中，當0被0除時，定義其結果為0。當次數k=4時，式(7)就簡化為雙3次B樣條的曲面方程。在進行動平衡測量系統的標定實驗中，首先選取多個測量轉速和多個轉子質量進行系統的標定操作，以獲取一組分布于節點(ω,A)上的標定結果值P(ω,A)：

(8)

ω4≤ω≤ωL+1,A4≤A≤AN+1

4 實驗結果與分析

實驗在德國申克公司的HY2BK動平衡機上配合ST590動不平衡電測箱進行。當輸入的動不平衡信號頻率為2～100Hz時，該電測箱測量精度可達到0.5g·mm/kg。系統采用磁電式傳感器檢測不平衡量引起的振動。

實驗中采用0.5kg、1.6kg、5kg、16kg四種不同質量的轉子，分別在轉速280、480、680、880、1080、1280、1480r/min下對動平衡機進行了標定操作，每一次標定按照式(5)進行，得到標定結果ρ11、ρ12、ρ21、ρ22。全部完成之后將獲得一組標定結果，然后沿測量轉速和轉子質量采用雙3次B樣條插值算法插值，獲取測量轉速范圍和質量允許范圍內任一點的系統標定系數。實驗后的插值標定結果如圖4所示。為了驗證采用雙3次B樣條插值進行標定的有效性和準確性，同時在轉速為380、580、780、980、1180、1380r/min時采用插值后的標定系數對系統進行驗證，將測量的結果與標準不平衡量進行對比，表1給出了測量的結果和測量的誤差。

從實驗數據可以看出：隨著測量轉速的升高，系統的標定系數也呈現出增大的趨勢，并且當轉速超過臨界值1100r/min左右時，標定系數會急劇增大，這表明與轉速有關的測量參數對系統的標定結果有重要的影響。當測量轉速更接近系統的固有頻率時，轉速對標定結果的影響就更加明顯。這也說明了測量轉速對動平衡測量和標定過程的影響是不可忽略的。

除此之外，從實驗結果還可以看出，當測量轉速比較低時轉子的質量對系統的標定結果幾乎沒有影響，只有當測量轉速超過某一臨界值時，轉子的質量才對系統的標定結果有明顯的影響。同時還能看出，轉子質量的影響比起測量轉速對系統標定結果的影響要小。在轉速比較低(遠遠低于系統的固有頻率)時系統的標定結果幾乎不受測量轉速和轉子質量的影響，這也同時驗證了通常的硬支承平衡機永久標定的適應性。當測量轉速在一個比較大的范圍內運行時，測量轉速和轉子質量對系統的測量和標定將帶來不可忽略的影響。

(a)標定系數ρ11

(b)標定系數ρ12

(c)標定系數ρ21

(d)標定系數ρ22圖4 標定系數的雙3次B樣條插值結果

在表1中，采用標準的不平衡試重進行測試驗證，將測量結果與不平衡量試重的標稱值進行了對比，其中最大的幅值誤差為4.2%，大多數的測量幅值誤差在2%以內，相位誤差大多在3°以內。采用基于雙3次B樣條插值標定后的系統測量精度與狀態標定后的系統測量精度基本一致，基于雙3次B樣條的標定方法可以實現較寬測量轉速范圍(軟支承和硬支承)內的永久標定。

表1 標定結果和測量結果

5 結語

實驗中的測量結果表明，動不平衡測量中，與測量轉速和轉子質量有關的測量條件對動不平衡系統的系統標定和測量結果有重要影響，尤其當測量轉速接近系統的固有頻率時，這種影響更加顯著。當測量的轉速范圍較寬時，某個轉速和某個質量的轉子的標定結果不能適用于整個測量范圍。采用有限個測量轉速和轉子質量進行系統標定，并將標定結果采用雙3次B樣條沿測量轉速和轉子質量進行插值，可以獲得足夠高的測量精度，實現轉子在軟支承和硬支承系統下的永久標定。

[1] 劉釗，任遠，陸文. 動平衡試重標定法的原理與應用[J]. 制冷空調與電力機械，2007(1): 70-72.

[2] 賀大拙. 二支座二配重面動平衡系統的快速平衡方案[J]. 中國空間科學技術，1981(3): 30-35.

[3] 周仕炎，肖之中.解決剛性轉子左右校正面影響問題的一個新途徑[J].試驗技術與試驗機，1982(4):4-9.

[4] 劉健，潘雙夏，楊克己. 動平衡機系統誤差分析及標定方法研究[J]. 組合機床與自動化加工技術，2004(4): 1-3.

[5] Qin P, Cai P. A Novel Vibration System Based on Instantaneous Motion Center for High Accuracy Dynamic Balancing Measurement of Outboard Rotor[J]. Proc. ImechE，Part C: J. Mechanical Engineering Science, 2009, 223(2): 387-395.

[6] Cox M G. The Numerical Evaluation of B-splines[J]. Journal of Applied Mathematics， 1972,10(2): 134-149.

[7] Prautzsch H, Boehm W, Paluszny M. Bezier and B-Spline Techniques[M]. Berlin：Springer, 2002.