遺傳算法在NURBS曲線擬合精度的研究應用

張銀娟 王永科

(許昌學院電氣信息工程學院1，河南 許昌 461000;許昌恒源發制品股份有限公司技術中心2，河南 許昌 461000)

0 引言

在科學數據的處理過程中，參數化技術給科學數據的處理帶來了極大的便利。非均勻有理B樣條(non-uniform rational B-splines，NURBS)曲線以其優良的性能受到廣大計算機輔助設計(computer aided design，CAD)工作者的青睞。NURBS曲線法通過操縱控制頂點和權值的方式，為曲線形狀調整提供了充分的靈活性;同時NURBS曲線的修正也引起了業界的廣泛重視。Piegl從NURBS曲線的數學定義出發［1］，提出了基于權因子的曲線形狀修正方法。眾多科技工作者分別從幾何角度分析了一個權因子和兩個權因子的變化對NURBS曲線曲面形狀的影響［2－6］。

由于權因子的不合理應用可能導致精度不足的曲線擬合，甚至破壞曲線的結構，因此，在曲線擬合過程中引入遺傳算法。由于遺傳算法計劃將字符串推廣到計算機程序［7］，尤其是采用符號回歸技術直接對數學表達式進行操作，能夠建立描述復雜系統的數學表達式模型，這就使得將遺傳算法引入到權因子對NURBS曲線的擬合精度控制成為一種可能。通過遺傳算法的全局并行搜索方式，搜索到權因子變化空間中的最優個體，從而對擬合函數的參數值進行優化。

1 權因子對NURBS曲線的影響

一條控制頂點為Vi(0≤i≤n)的NURBS曲線P(u)可表示為:

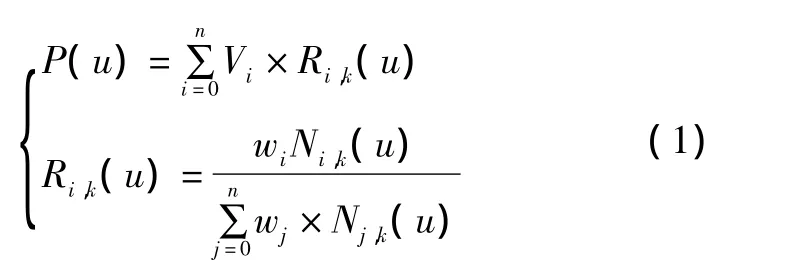
式中:wi(0≤i≤n)為依附于相應控制頂點Vi(0≤i≤n)的權因子，一般約定首末權因子w0和wn≥0，其余權因子wi＞0(1≤i≤n－1)，以防止表達式方程分母為0，保證了曲線的凸包性質，并避免曲線因為權因子的取值而退化為一點這類現象的發生;Ni，k(u)為第i個k次規范B樣條基函數，它定義在節點矢量U={u0，u1，…，un+k+1}上;Ri，k(u)為權因子 w 和基函數Ni，k(u)的表達式，它表示的是曲線P(u)計算過程的一個中間運算式。

為分析權因子wi的幾何意義，可以假設只有wi發生變化，其他變量均不變，同時設定B、N、B(i)分別為 wi=0、wi=1、wi∈(0，1)∪(1，∞)的對應 NURBS曲線上的點。權因子影響示意圖如圖1所示。

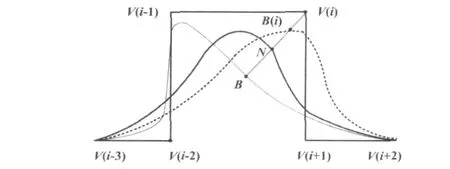
圖1 權因子影響示意圖Fig.1 The effects of weight factors

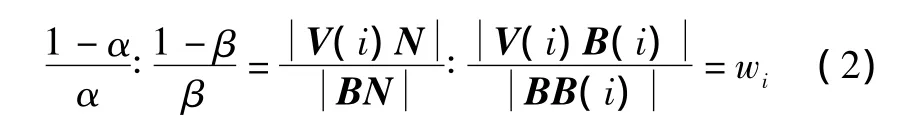
由圖1和式(2)可以得出權因子wi對NURBS曲線形狀的影響，具體介紹如下。

①當增大(減小)權因子wi，曲線被拉向(推離)控制頂點V(i)。

②當wi=0時，此時控制頂點V(i)對曲線沒有控制作用;當 wi趨于無窮大時，曲線經過控制頂點V(i)。

③ 當wi連續變化時，B(i)點隨之連續變化，軌跡為一條直線。

考慮到權因子對曲線的形態的影響，權因子選擇不當可能導致誤差較大的NURBS曲線擬合，本文采用最小二乘性能指標來表征NURBS曲線的擬合精度。當隨機給定權因子 w=［3.5，1.7，2.2，6.5，0.9，1.5，4.9，2.5］時，NURBS 曲線擬合的最小二乘性能指標為1.3007，此時權因子和控制頂點也能大致反映控制頂點數據的結構。為了更精確地反映控制頂點的曲線趨勢，下文將引入遺傳算法。隨機權因子NURBS擬合曲線如圖2所示。

令 α=Ri，k(u;wi=1)和 β=Ri，k(u)，則有 N=(1 －α)B+αV(i);B(i)=(1－β)B+βV(i)，得到如下恒等式:

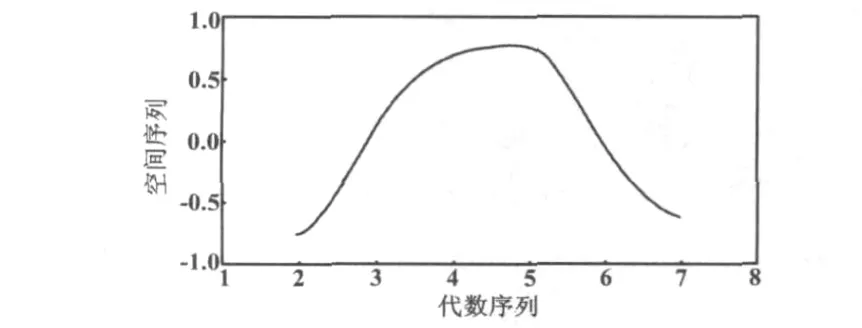
圖2 隨機權因子NURBS擬合曲線Fig.2 NURBS curve fitting with stochastic weight factors

2 遺傳算法原理

遺傳算法以自然選擇和遺傳理論為基礎，它是一種將生物進化過程中適者生存規則與群體內部染色體的隨機信息交換機制相結合的高效全局尋優搜索算法。目前，遺傳算法得到迅速的發展，其主要的應用領域有生命的遺傳進化、人工智能、生產規劃、模式識別、圖像特征提取、濾波器設計、機器人控制和防避導彈控制等領域;同時，遺傳算法也成為求解優化問題的有力工具之一。

遺傳算法的應用過程是將問題域中的可能解看作群體的一個個體或染色體，并將每一個個體編碼成符號串的形式，模擬達爾文的遺傳選擇和自然淘汰的生物進化過程，對群體反復進行基于遺傳學的操作［8－9］;同時，根據預定的目標適應度函數對每個個體進行評價，依據適者生存、優勝劣汰的進化規則，不斷得到更優的群體，并采用全局并行搜索方式來搜索優化群體中的最優個體，求得滿足要求的最優解。

遺傳算法的應用步驟如下。

①確定個體的表現型X和問題的解空間;

②確定目標函數的類型及數學描述形式或量化方法;

③確定個體的基因型及遺傳算法的搜索空間;

④確定個體基因型x映射到個體表現型X的對應關系或轉換方法;

⑤確定目標函數值f(x)映射到個體適應度F(X)的轉換規則;

⑥確定選擇運算、交叉運算和變異運算等基本遺傳算子的具體操作方法;

⑦問題解的解空間尋優過程，尋優過程完成后確定最優解。

3 最優權因子的求解

權因子對曲線形態有著重要影響，不合適的權因子會導致NURBS曲線失去意義。本文將遺傳算法引入到權因子對NURBS曲線的擬合精度控制中，通過遺傳算法的全局并行搜索方式，搜索到權因子變化空間中的最優個體，從而對擬合函數的參數值進行優化。

3.1 權因子求解步驟

最優權因子求解過程如下。

①建立優化模型，確定決策變量解空間范圍和約束條件。

②確定編碼方法，用長度為10位的二進制串碼(b1，b2，…，b10)分別表示決策變量，其中10位二進制串碼代表0～1023之間的1024個不同數值，同時將決策變量定義域離散化為1023個均等區域。根據解空間的取值范圍，離散點0到離散點10.23依次分別對應二進制串碼0000000000～1111111111之間的二進制串碼。這些二進制串碼構成了次優化問題的染色體編碼。

③確定解碼方法，解碼時，根據編碼方法和離散化方法，設定 bi∈(b1，b2，…，b10)，Umin和 Umax分別代表十進制串碼的最小值和最大值，則每十位二進制串碼分別映射到十進制的數值代碼W的解碼公式為:

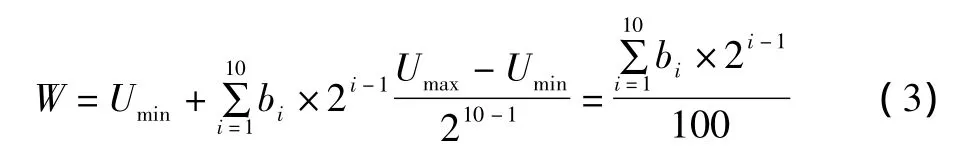
④確定個體評價方法，針對曲線擬合的精度問題，運用最小二乘法。該問題的優化目標就是求解給定曲線和擬合曲線的最小二乘值最小。

⑤設計基本遺傳算子，選擇運算使用比例選擇算子，交叉運算使用單點交叉算子，變異運算使用基本位變異算子。

⑥確定遺傳算法的運行參數。

3.2 仿真試驗

采用上述遺傳算法步驟，設定群體大小為80，終止進化迭代數為500，交叉概率為0.60，變異概率為0.10，則迭代運算500步。算法迭代仿真試驗完成后，最佳權因子NURBS擬合曲線和性能指標最小變化過程曲線分別如圖3和圖4所示。

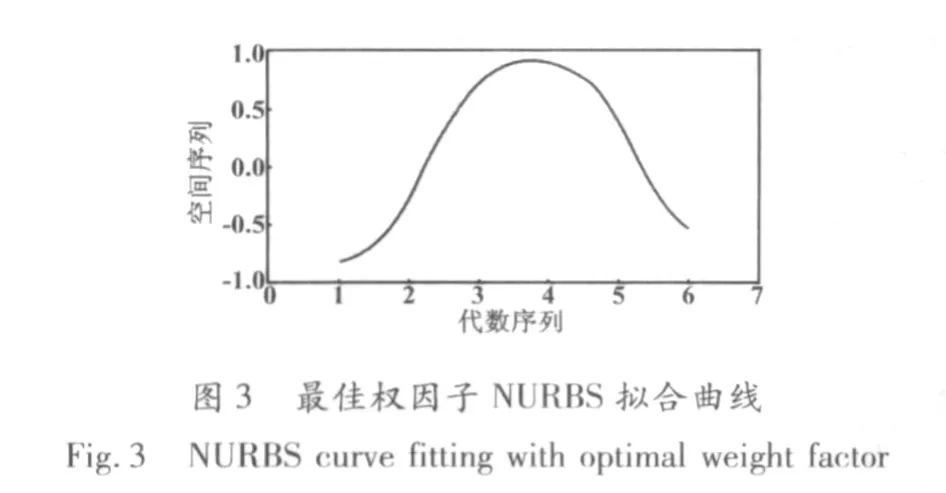
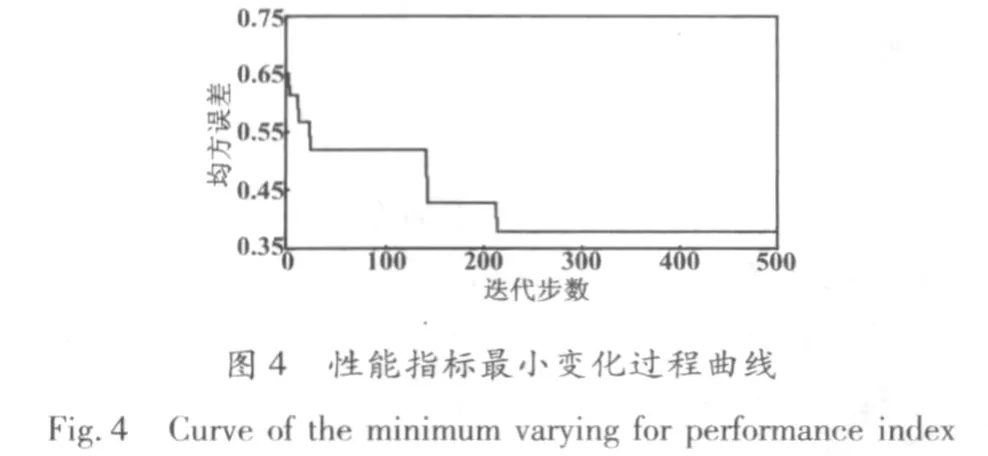
從圖4可以看出，遺傳算法在運算開始的一段時間內，效果很明顯。隨著進化迭代次數的增加(進化過程的進行)，同時由于選擇、交叉和變異機制的作用，群體中適應度低的一些個體被淘汰，而適應度高的一些個體則越來越多，并且都集中在所求問題的最優點附近。在迭代運算完成后，算法全局搜索到的最佳權因子樣本為 ［0.41，8.64，3.45，3.81，10.11，3.22，4.13，1.79］，此時最小二乘性能指標僅為0.3276，相比隨機權因子NURBS曲線擬合性能指標1.3007有了較大提高。因此，遺傳算法全局搜索到的最優解使得曲線擬合精度有了較大的改善。

4 結束語

遺傳算法摒棄了傳統的搜索方式，模擬自然界生物進化過程，采用人工進化的方式對NURBS權因子空間進行隨機全局搜索和優化;使用適者生存的原則，從潛在的解決方案種群中依次產生一個近似最優的方案，從而對NURBS曲線擬合的權因子進行優化。當然，遺傳算法的NURBS曲線擬合還有很多需要改進的地方，如對參數的編碼可以采用整數或字母排列的方式，對曲線和曲面的擬合也可以用熵性能指標作為適配值［10－12］。相信在不久的將來，通過對遺傳算法進行改進和完善，使其有望在設計和工程運用中發揮更大的作用及優勢。

［1］Piegl L，Tiller W.Curve and surface constructions using rational B-sphine［J］.Computer Aided Design，1987，19(9):485 －498.

［2］戴春來.樣條曲線的參數化變形方法［J］.計算機輔助設計與圖形學學報，2005，17(6):1207 －1212.

［3］龔晨.曲線的隨機擬合及其自適應算法［J］.上海交通大學學報:自然科學版，2005，39(4):661 －664.

［4］陳國振，劉靜華.B樣條曲面自適應擬合算法［J］.北京航空航天大學學報:自然科學版，2007，33(2):210 －213.

［5］蘇翩，林意，邱利瓊，等.NURBS曲線的一種快速修正算法［J］.重慶大學學報:自然科學版，2007，30(4):118－120.

［6］孫玉文，吳宏基，劉健.基于NURBS的自由曲面精確擬合方法研究［J］.機械工程學報，2004，40(3):10 －14.

［7］張善文，劉建都，韓小斌.基于遺傳算法的一種數據擬合方法［J］.空軍工程大學學報:自然科學版，2007，8(1):66 －68.

［8］梁芳，王衛華，祝慶.改進的遺傳算法在Logistic曲線擬合中的應用［J］.武漢理工大學學報:信息與管理工程版，2008，30(4):544 －547.

［9］周明華，汪國昭.基于遺傳算法的B樣條曲線和Bézier曲線的最小二乘擬合［J］.計算機研究與發展，2005，42(1):134 －143.

［10］吳景龍，楊淑霞，劉承水.基于遺傳算法優化參數的支持向量機短期負荷預測方法［J］.2009，40(1):180－184.

［11］陳果.基于遺傳算法的支持向量機分類器模型參數優化［J］.機械科學與技術，2007，26(3):347 －350.

［12］唐煒，張莉，陳濤.遺傳優化支持向量機的傳感器動態建模［J］.自動化儀表，2011，32(3):21 －23.