時柵位移傳感器的誤差分離與補償方法研究

彭東林 孫世政 高忠華 陳錫侯 楊繼森 鄭方燕

(重慶理工大學機械檢測技術與裝備教育部工程研究中心，重慶 400054)

0 引言

時柵傳感器是一種全新的位移傳感器［1－2］，它實現了以時間測量空間的功能。但由于溫度漂移、電子元器件的不穩定性、機械加工誤差等各種不確定因素的存在，影響了時柵精度的進一步提高。時柵傳感器的誤差產生具有一定的規律性和確定性，因此，可以通過補償方法對誤差加以消除或抑制［3－5］。誤差分離補償技術在測角系統中被廣泛采用，本研究試圖通過分析時柵傳感器測角系統的誤差組成，研究誤差的分離方法和基于最小二乘法的誤差補償方法，從而大幅度提高時柵角位移的測量精度。分離為n次誤差諧波的疊加之和［6］。因此，運用傅里葉級數分離法，測角系統的誤差公式可表示為:

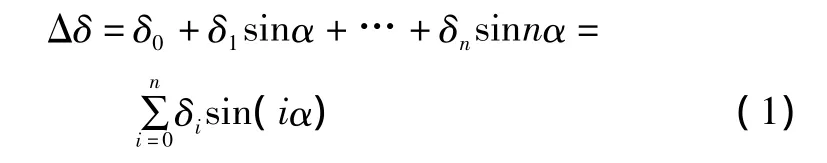
式中:Δδ為測角系統的誤差;n為誤差展開為傅里葉級數的次數;α為時柵測量系統所測量的角度值。

由式(1)可以看出，傅里葉變換的實質是將Δδ這個波形分解成許多不同頻率的正弦波的疊加［4－6］。此時系統的綜合誤差與傅里葉級數是一致的，分離誤差可以直接采集若干位置的對應誤差;然后進行傅里葉變換，通過式(1)，即可得出誤差的規律;最后對測量誤差進行補償。

1 時柵測量系統的誤差分離

2 誤差補償的實現

傅里葉變換被大量使用在工程中，尤其是應用在旋轉機械設備的故障診斷和誤差分析過程中。時柵角位移測量系統的誤差可被視為是n次誤差諧波的疊加，而按照傅里葉變換的思想，可以將測量系統的誤差

2.1 補償模型的建立

最小二乘法是一種廣泛應用在多學科領域中的數據處理方法，它既可用于線性參數的處理，又可用于非線性參數的處理。

由于測量數據不可避免地包含測量誤差，所以為了提高所得結果的精度，應適當增加測量次數，從而利用抵償性減少隨機誤差的影響。將式(1)寫成矩陣的形式，則有:

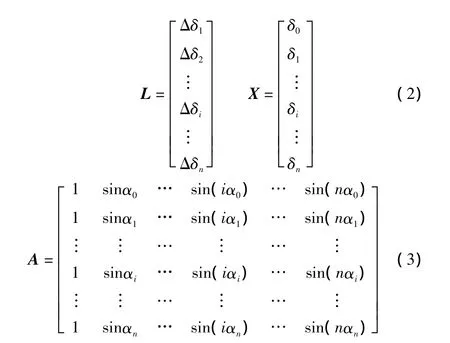
根據最小二乘法原理，測量結果的最可信賴值應在殘余誤差平方和最小的條件下求出，故引入殘余平方和矩陣V(V=L－AX)。在等精度測量時，殘余誤差平方和VTV為最小的條件即(L－AX)T(L－AX)為最小［7－8］。

2.2 最小二乘法的實現

將式(1)轉換為矩陣形式L=AX，則可視為將誤差的非線性轉換為線性，然后運用擬合的方法，采用n次諧波來逼近反非線性曲線。矩陣A在諧波次數為n和采樣點個數確定的情況下可以通過計算求得，而矩陣L中的基準誤差可以通過光柵測量得到。根據最小二乘法原理，在殘差平方和VTV最小的條件下，可以求解出矩陣X，從而得出誤差的曲線規律。采樣點數量的選擇由擬合的諧波次數決定，在諧波次數一定的情況下，采樣點要大于未知數的個數。采樣點越多，擬合的曲線就越接近真實情況。

3 軟件實現

誤差補償算法流程如圖1所示。

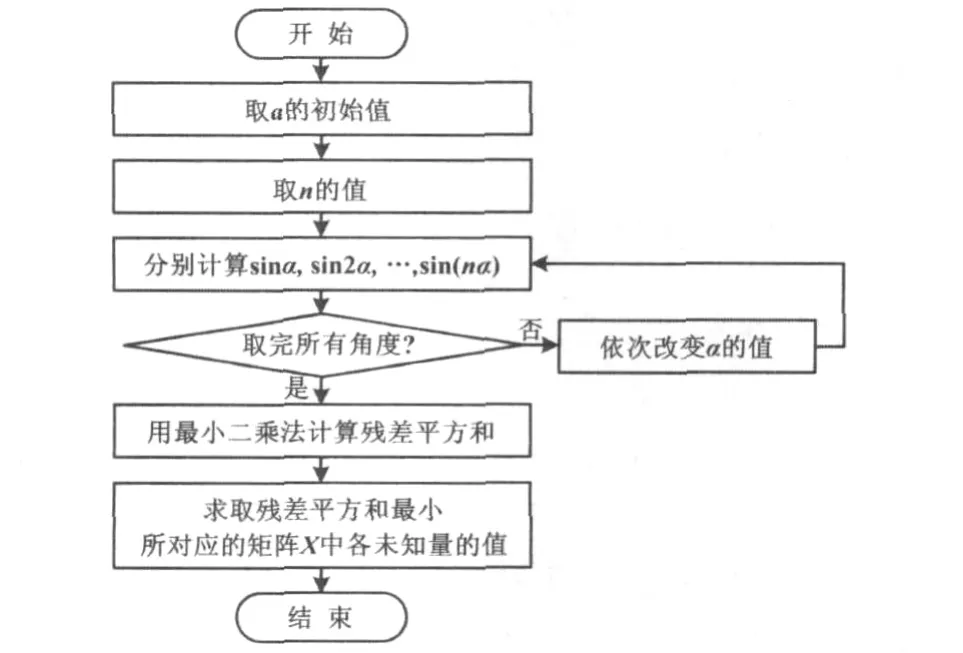
圖1 算法流程圖Fig.1 Flowchart of algorithm

本文采用Matlab7.1編程軟件，在系統的誤差補償中采用的是軟件補償的方法，具體包括取測量角度和諧波次數的初始值、各次諧波的計算、殘差平方和的計算以及參數計算等模塊。

運用該方法進行誤差分離時，需根據經驗或已測得的數據判斷測量系統誤差的主要成分，即要先確定最高次諧波的諧波次數n，并在殘差平方和為最小的條件下求出方程中的未知量，進而對誤差規律進行擬合。該方法能夠較快地找到誤差的可信規律，其最終結果能充分利用誤差的抵償作用，從而有效減少隨機誤差的影響，具有可信賴性［9－11］。通過對時柵傳感器誤差曲線進行修正，使時柵傳感器的測量精度得到進一步提高。

4 試驗與測試實例

時柵傳感器誤差的測量是以高精度光柵作為角度測量的基準。將光柵和時柵傳感器分別通過彈性聯軸結安裝在精密分度轉臺的主軸上，隨轉臺同時轉動。伺服電機通過同步帶輪帶動轉臺做勻速轉動的同時，也使光柵和時柵同時轉過相應的角位移，每轉動一個位置，分別讀取光柵和時柵測量所得的角度值，兩者的差值就是時柵測角系統的原始誤差。本研究中用于測試的時柵傳感器選用海德漢公司生產的光柵，其型號為TGS132F型。該光柵的測量精度可達到±1″。試驗過程中，在整周360°內共測試了720個位置點，部分采樣點數據如表1所示。以第一組數據為例，它表示的是將轉臺轉過固定角度，當時柵測量的角度值為0°00'00″時，光柵測量的角度值為 0°00'03″4，它們存在的誤差值為 －3.1″。

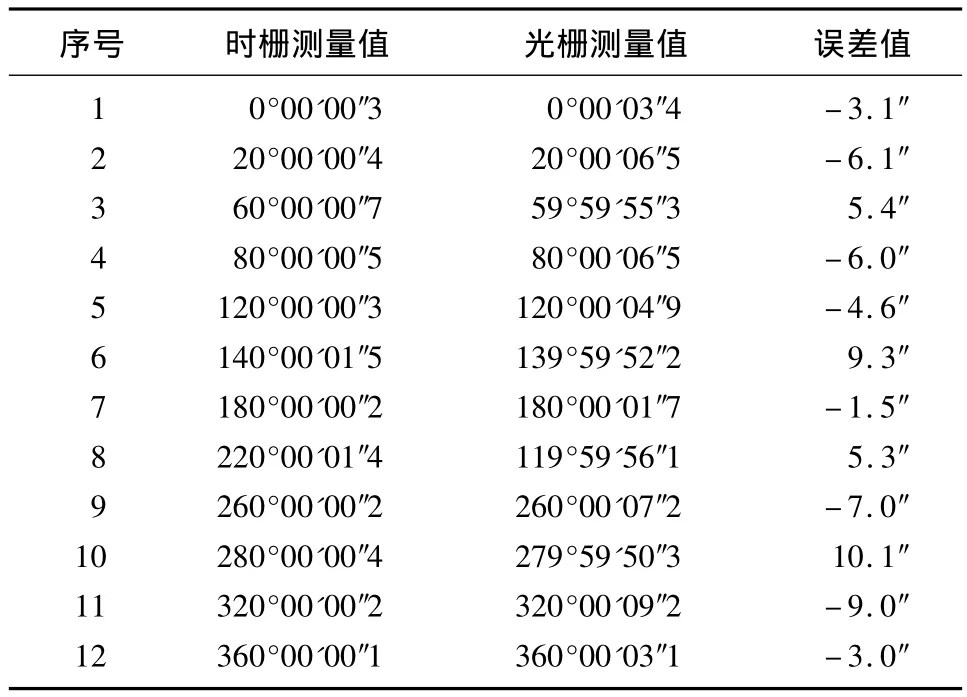
表1 部分采樣點數據表Tab.1 Partial data sample data

對應的空間角度測量誤差曲線，即未修正的測量誤差曲線如圖2所示。

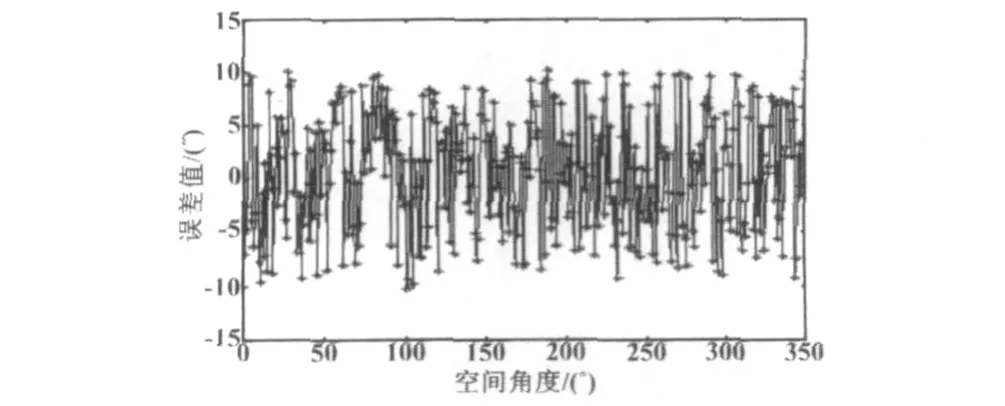
圖2 未修正的測量誤差曲線Fig.2 The error curve before correction

試驗證明，時柵角位移測量系統的測量誤差的主要成分是低次諧波誤差。當選取諧波次數n=10時，擬合的誤差規律曲線與實際的誤差曲線擬合度最好。對所得的擬合誤差曲線再進行誤差補償，得到的曲線如圖3所示。

從圖2和圖3可以明顯看出，補償前后誤差范圍從 ±10.2″降到 ± 2.1″，誤差修正的結果說明該補償方法對本系統起到了很好的誤差補償作用。

5 結束語

本文針對時柵角位移測量系統中的誤差特性進行分析，提出了基于最小二乘法的誤差分離和補償模型，并運用該模型對使用的時柵測角系統進行誤差補償。在實際的傳感器生產過程中［12－13］，通過運用軟件對時柵角位移測量系統中存在的誤差進行補償，有效地節約了生產成本和生產時間，并在一定程度上提高了時柵角位移測量系統的測量精度。

［1］彭東林.時柵位移傳感器與新型機床動態檢測系統［M］.北京:科學出版社，2010:56－69.

［2］彭東林，張興紅，劉小康，等.場式時柵位移傳感器研究［J］.儀器儀表學報，2003，24(3):321 －323.

［3］陳自然，彭東林，王先全，等.基于Matlab的時柵位移傳感器的誤差曲線分析與擬合研究［J］.工具技術，2008，42(12):85 －88.

［4］張天恒，彭東林，楊偉，等.時柵傳感器電氣誤差分析及補償［J］.工具技術，2009，43(8):107 －109.

［5］彭東林，劉小康，張興紅，等.高精度時柵位移傳感器研究［J］.機械工程學報，2005，41(12):126 －128.

［6］冷建華.傅里葉變換［M］.北京:清華大學出版社，2004:15－26.

［7］費業泰.誤差理論與數據處理［M］.5版.北京:機械工業出版社，2004:94－98.

［8］費業泰，陳曉懷.精密測試及儀器的誤差修正技術［J］.宇航計測技術，2006，16(4－5):66－70.

［9］李金海.誤差理論與測量不確定度評定［M］.北京:中國計量出版社，2003:1－59.

［10］譚久彬.精密測量中的誤差補償技術［M］.哈爾濱:哈爾濱工業大學出版社，1995:18－20.

［11］李秋明，馮汝鵬，王景賀，等.感應同步器測角系統誤差分析及補償［J］.中國慣性技術學報，1998，6(1):50 －54.

［12］張星，白強，夏善紅，等.小型三維電場傳感器設計與測試［J］.電子與信息學報，2007，29(4):1003 －1004.

［13］唐海，行鴻彥，季鑫源.大氣電場儀中相敏檢波器的分析設計［J］.現代電子技術，2009，30(13):8－10.