中國物流業周期的共變性和非對稱性特征＊

賀興東 劉 凱 邵偉如

（北京交通大學交通運輸學院1） 北京 100044） （河北交通職業技術學院2） 石家莊 050091）

Burns和Mitchell提出了經濟周期存在共變性和非對稱性2個典型化特征［1］．Hamilton的機制轉換模型［2］則對各單一經濟變量的非對稱性進行研究．Diebold和Rudebusch，Kim和 Nelson，Kim和 Murray，Kim 和Piger，Murray和Piger則致力于建立一種能夠將經濟周期的共變性和非對稱性特征同時進行分析的模型［3－8］．物流業是宏觀經濟中的獨立產業之一，但由于缺乏必需的表征指標和統計數據，致使關于物流業周期的共變性和非對稱性特征的研究成果尚不多見．最近賀興東、劉凱和陸華得到了一組物流一致指標和一個物流運行指標，為物流業周期的共變性和非對稱性特征研究提供了條件．本文對中國物流業周期的共變性和非對稱性特征進行識別，得出中國物流業周期的共變性和非對稱性的實證分析結果．

1 基于馬爾科夫機制轉換的多變量動態因子模型

1．1 模型說明

令Yit為第i個物流一致指標的對數，i＝1，2，3，4；Ct為不可觀測的物流公共周期因子的對數，則基于馬爾科夫機制轉換的多變量動態因子模型如下．

式中：Δ為差分算子，則ΔYit為第i個物流一致指標的增長率；ΔCt為物流公共周期因子增長率；ΔTit為第i個物流一致指標自有成分的增長率；γi為物流公共周期因子增長率ΔCt在第i個物流一致指標中所占權重．

假設ΔCt由長期趨勢項和機制轉換項組成，且服從式（2）過程

式中：wt對各時間下標t相互獨立，且均遵循期望為0，方差為1的正態分布．μst的取值取決于t時刻物流業處于收縮期（st＝0）還是擴張期（st＝1），如下

而物流業運行收縮和擴張之間的機制轉換遵循如下馬爾科夫過程

假設ΔTit由一個常數項和一個AR（2）過程組成，即

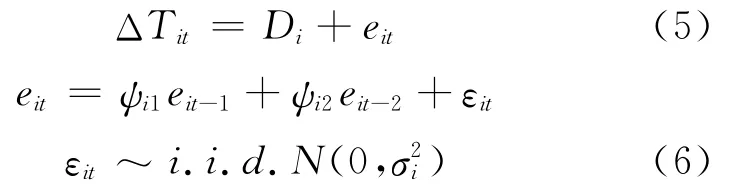
式中：εit與wt對所有t和i而言相互獨立．

由于Di和σi是超參數，使得上述模型不可識別．為此將各指標數據標準化，則式（1）、式（2）、式（5）、式（6）變為

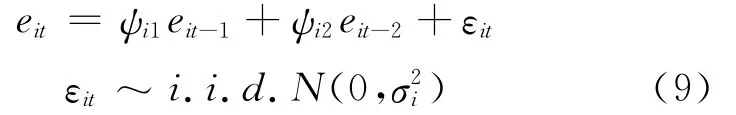
其中：Δyit＝ΔYit－Di－γiδ，Δct＝ΔCt－δ．

式（7）～（9）、式（3）和式（4）就組成了基于馬爾科夫機制轉換的多變量動態因子模型．

1．2 模型的狀態空間形式

上述基于馬爾科夫機制轉換的多變量動態因子模型可以表示為狀態空間形式．模型的狀態空間形式并不唯一，根據參數估計需要，令＝Δyit－ψi1Δyit－1－ψi2Δyit－2，i＝1，2，3，4，φ（L）＝1－φ1L－φ2L2，L為滯后算子，本文給出如下兩種形式的狀態空間模型．

1）狀態空間形式1

測量方程

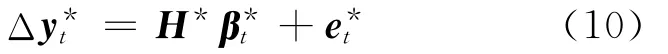
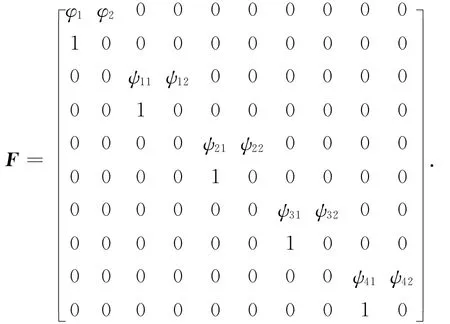
轉移方程

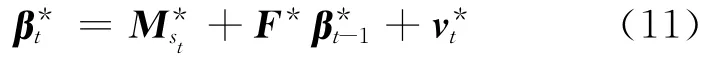
其中：

2）狀態空間形式2

測量方程

轉移方程

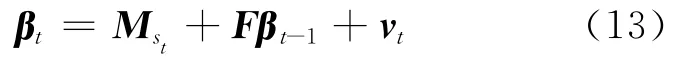
式中

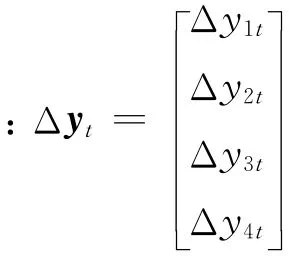
2 模型參數估計的基于貝葉斯推斷吉布斯抽樣法

給定狀態空間形式，模型的參數估計可采用基于貝葉斯推斷的吉布斯抽樣方法．參數估計的目標是從四個物流一致指標數據中推斷出以下參數：（1）物流公共周期因子增長率 ΔCt，t＝1，2，…，T的路徑，用Δ表示；（2）馬爾科夫機制轉換變量st，t＝1，2，…，T 的路徑，用表示；（3）模型的其他未知參數，用~θ表示．基于貝葉斯推斷參數估計首先將上述3種參數均視作隨機變量向量，然后在這些隨機變量向量的歷史數據（隨推斷過程而不斷更新）和4個物流一致指標的數據給定的條件下，通過對這些隨機變量的聯合分布求和的方法獲得這些隨機變量的推斷值．而這些隨機變量的聯合分布無法直接得到，需先利用吉布斯抽樣方法得到各隨機變量關于其余隨機變量的條件分布．

利用基于貝葉斯推斷的吉布斯抽樣方法估計，本文的多變量動態因子模型的步驟如下．

步驟1 給定模型參數~θ值．

步驟2 利用模型的狀態空間形式1，在~sT，~θ和物流一致指標數據已知的條件下，推斷Δ~cT．

步驟3 在Δ~cT和物流一致指標數據已知的條件下，推斷模型參數ψi1，ψi2，σ2i和γi，i＝1，2，3，4．

步驟4 在Δ~cT已知的條件下，推斷~sT以及模型其他參數p，q，μ0，μ1，φ1和φ2．

步驟5 利用模型的狀態空間形式2，在~sT，~θ和物流一致指標數據已知的條件下，計算物流公共周期因子增長率Δ~CT路徑．

上述5個步驟不斷迭代直至滿足精度要求，便可獲得模型的參數，同時提取出了物流公共周期因子增長率Δ~CT路徑．

3 實證分析：中國物流周期的共變性和非對稱性特征

3．1 參數估計結果

本論文中用到的中國物流運行表征指標和4個一致指標來源于賀興東、劉凱和陸華（2011）的研究．中國物流運行表征指標是物流運行指數（PLOI），是綜合表征物流業運行特征的指標．4個一致指標分別是全國貨運周轉總量指數（FTKI）、全國貨運總量指數（FTI）、交通運輸倉儲和郵政業增加值指數（VATSPI）以及合成物流業務量總額指數（CTLVI），分別從物流業運行的各個方面表征其運行特征．

按照上節算法步驟編寫程序進行參數估計，選用的程序平臺為計量經濟學軟件Guass5．1．舍棄前2 000次模擬結果，應用之后10 000次模擬結果計算模型參數的后驗分布，可保證參數估計的結果不受初值影響．參數估計結果見表1．

3．2 中國物流周期的共變性特征

將本文模型計算得到的中國物流公共周期因子增長率路徑Δ~CT與中國物流運行指數（PLOI）表征的物流周期路徑繪制出來，如圖1所示，其中實線為Δ~CT，虛線為中國物流周期路徑．可見絕大多數時間內兩條路徑均十分接近，說明中國物流周期具有明顯的共變性特征．

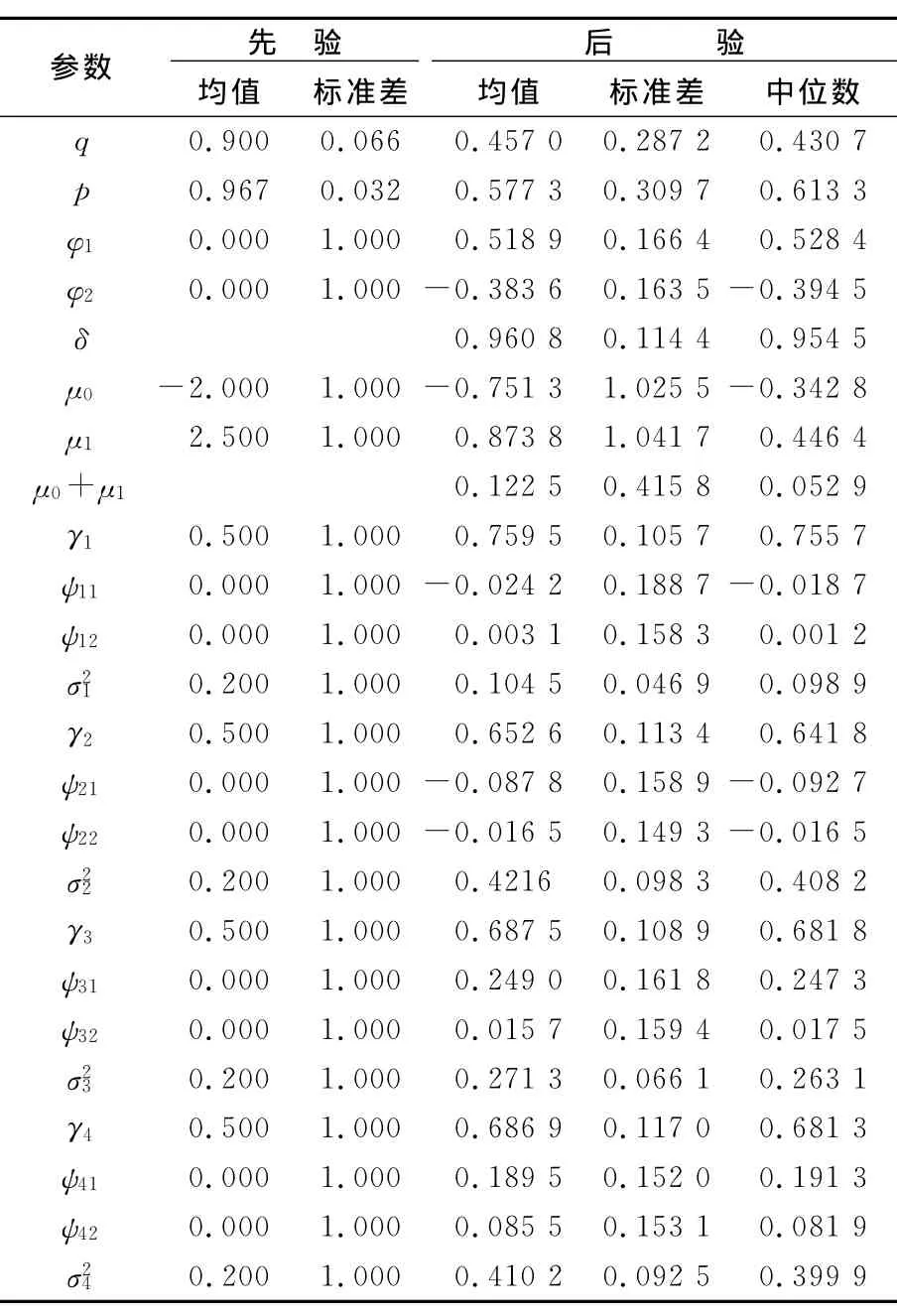
表1 中國物流周期多變量動態因子模型參數估計結果

圖1 中國物流業周期路徑對比

3．3 中國物流周期的非對稱性特征

圖2 所示為本文的多變量動態因子模型計算得到的中國物流業運行中的收縮概率，可見平均收縮概率明顯低于0．5，同時意味著平均擴張概率明顯高于0．5，收縮和擴張概率并不對稱．此外，由模型平均收縮概率和平均擴張概率計算的到的平均收縮時間和平均擴張時間分別為1／（1－q）＝1．84年和1／（1－p）＝2．36，平均收縮時間和平均擴張時間也不對稱．說明中國物流周期具有明顯的非對稱性特征．

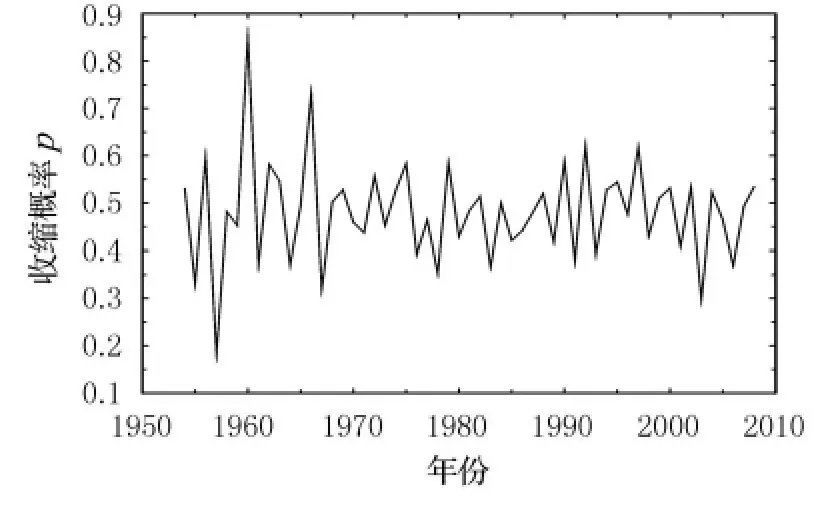
圖2 歷年中國物流業運行的收縮概率

4 結束語

本文對中國物流業周期的共變性特征和非對稱性特征進行識別．給出了可同時進行共變性特征和非對稱性特征識別的基于馬爾科夫機制轉換的多變量動態因子模型，并設計了模型參數估計的基于貝葉斯推斷的吉布斯抽樣方法．得到了表征物流業周期共變性的物流公共周期因子增長率和刻畫物流業周期非對稱性的物流運行收縮概率．對中國物流業周期的共變性特征和非對稱性特征進行了識別，結果發現：大多數時間內中國物流公共周期因子增長率路徑與物流業周期路徑十分接近，說明中國物流業中期具有顯著共變性特征；同時，中國物流業運行的平均收縮概率與平均擴張概率明顯不同，周期平均收縮長度與平均擴張長度的差異也較明顯，說明中國物流業周期同時具有顯著的非對稱性特征．

［1］Burns A M，Mitchell W C．Measuring business cycles［R］．New York：National Bureau of Economic Research，1946．

［2］Hamilton J．A new approach to the economic analysis of nonstationary time series and the business cycle［J］．Econometrica，1989，57（2）：357－384．

［3］Diebold F X，Rudebusch J D．Measuring business cycles：a modern perspective［J］．Review of Economics and Statistics，1996，78（1）：67－77．

［4］Kim C J，Nelson C R．Business cycle turning points，a new coincident index，and tests of duration dependence based on a dynamic factor model with regime switching［J］．The Review of Economics and Statistics，1998，80（2）：188－201．

［5］Kim C J，Nelson C R．State－space models with regime switching classical and gibbs－sampling approaches with application［M］．London：Massachusetts，Cambridge，MITPress，1999．

［6］Kim C J，Murray C J．Permanent and transitory components of recessions［J］．Empirical Economics，2002，27（2）：163－183．

［7］Kim C J，Piger J．Common stochastic trends，common cycles，and asymmetry in economic fluctuations［J］．Journal of Monetary Economics，2002，49（6）：1 189－1 211．

［8］Kim C J，Murray C J，Piger J．Nonlinearity and the permanent effects of recessions［J］．Journal of Applied Economics，2005，20（2）：291－309．