半潛平臺結構疲勞壽命評估方法比較

楊 鵬，顧學康

(中國船舶科學研究中心，江蘇 無錫214082)

0 引 言

結構疲勞壽命評估是海洋結構物設計安全性評估的關鍵內容之一，如何準確有效地評估半潛式海洋平臺的結構疲勞壽命是目前海洋工程界的一個難點。經典的結構疲勞壽命評估方法一般基于線性累積損傷原理和結構節點的S－N 曲線方法［1－3］，當前各大船級社［4－5］均推薦使用S－N 曲線方法進行船舶和海洋平臺的結構疲勞壽命評估，有些船級社還使用斷裂力學方法進行剩余疲勞壽命的評估。雖然S－N 曲線缺乏嚴格的理論依據且評估精度略差，但是由于經過了很長時間的發展，在工程上應用較為成熟。斷裂力學方法能從機理上解釋大量的疲勞現象，并且已經發展出了各種裂紋擴展模型，但是由于裂紋擴展機理本身十分復雜，因而現今還沒有十分完善的模型和理論。然而斷裂力學方法是最有希望解釋清楚疲勞裂紋擴展現象的一種工具，因此很多學者一直致力于發展出可以更加精確的評估結構疲勞壽命的裂紋擴展模型。在海洋工程結構物疲勞壽命評估方面S－N 曲線方法和斷裂力學方法存在多大的差別是有待研究考查的一個問題。另外，海洋結構物在隨機波浪載荷作用下所承受的疲勞載荷的預報方法也有很多種模型，如譜分析方法、設計波方法、時域計算方法和DISAM 方法等［6］。譜分析計算方法簡潔、高效，但是主要用于線性情況下。而時域計算方法過程合理但是計算費時，線性和非線性情況下均可使用。設計波方法是最為高效的方法，只需要給定一個或幾個規則波中的波浪載荷分布并施加到結構模型上，然后計算結構應力即可進行結構疲勞壽命評估。設計波法的難點在于針對不同的結構部位確定不同的主要波浪載荷類型以及確定設計波浪向、波長和波高。ISSC 疲勞專家委員會［6］認為垂向彎矩、水平彎矩、扭矩、橫向加速度和水動壓力等均有可能成為關鍵波浪載荷參數，對于不同的船型、平臺形式和構件，設計波浪載荷類型是不一樣的，需要經過大量的計算論證。

因此，為了探討S－N 曲線方法與斷裂力學方法以及譜分析方法與設計波法在海洋結構物疲勞壽命評估方面的差別，本文分別利用S－N 曲線方法和斷裂力學方法計算半潛式海洋平臺的疲勞壽命，分析比較二者計算結果的差別。同時比較了譜分析方法和設計波法的計算結果，找出在使用設計波方法計算半潛式海洋平臺典型節點的疲勞壽命時的主要波浪載荷參數，為半潛式海洋平臺結構疲勞壽命的合理評估提供依據。

1 熱點應力傳遞函數計算

某半潛式海洋平臺總長114 m，總寬78 m，上甲板距基線高38 m，工作工況下設計吃水19 m，排水量5 萬t，半潛式海洋平臺的Ansys 整體和局部結構模型如圖1所示。半潛式海洋平臺有很多關鍵節點的疲勞壽命需要評估，本文以撐桿與立柱相接處的局部結構為例，選定1 根撐桿與立柱相接處的典型節點A(見圖1)，進行疲勞壽命評估方法的比較與分析。

半潛式海洋平臺的波浪載荷可以使用三維線性波浪理論進行計算［7］，雖然半潛式平臺結構左右對稱，但是在左右對稱2 個浪向下，局部節點處的濕表面壓力并不相同;同時相對浪向情況下，對于結構濕表面雖然波浪輻射勢和入射勢是一樣的，但是繞射勢存在一定差別，于是以上2 種情況下波浪載荷作用中局部節點的結構應力并不相同，因此需要對全浪向進行計算。計算浪向選定從0° ～330°每30°計算1 次，總共12 個浪向。計算波浪圓頻率選定從0.01 ～1.6 rad/s，每0.05 rad/s計算1 次，總共31 個頻率，該頻率段包含了波浪的主要能量。

在單位波幅規則波下計算得到平臺濕表面水動外壓力和平臺整體慣性力，水動外壓力和平臺整體慣性力按實部和虛部分別施加到平臺整體有限元模型上。因計算平臺濕表面水動壓力的粗網格與平臺外殼有限元模型的細網格不匹配，因此需要編制相應的水動壓力載荷轉換程序。通過轉換程序計算平臺濕表面上每個有限元單元的水動壓力，然后使用APDL 語言編制相應的ANSYS 程序用于每個工況下的有限元結構應力計算和結構熱點應力提取，同時應力選自shell63 單元的上表面。因為有12 個浪向，31 個頻率，為了考慮不同部位水動壓力相位的影響，響應計算分實部和虛部，取模即為熱點應力幅值，所以總共需要進行744 次有限元應力計算。

有限元模型整體采用粗網格，在熱點附近細化網格。熱點處網格大小取板厚大小，網格尺寸依次向外平滑過渡，最后的有限元網格數約為10 萬個。施加到有限元單元上的載荷有濕表面水動壓力載荷和平臺整體慣性力，然后在遠離熱點應力的結構上施加邊界條件。計算得到的典型節點A 處各個浪向下的熱點應力幅值Hs 的傳遞函數如圖2所示。

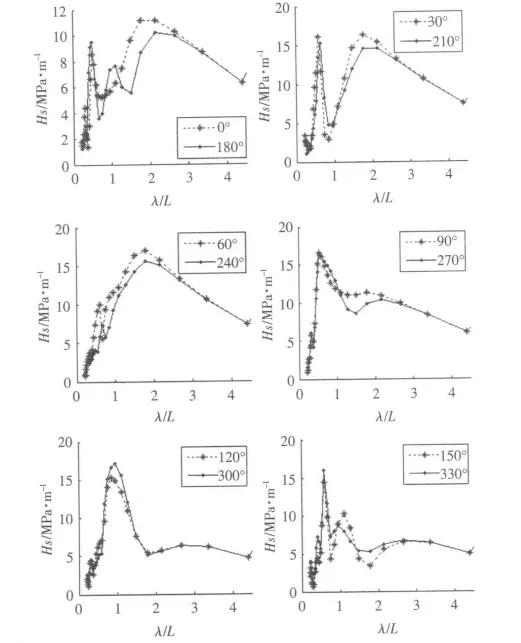
圖2 熱點應力幅值傳遞函數Fig.2 Transfer functions of stress amplitude at hot-spots

2 譜方法計算結構疲勞壽命

馮國慶［8］對疲勞強度評估中的譜方法流程進行了詳細闡述，而馬網扣［9］針對半潛式海洋平臺典型節點的疲勞強度進行了譜分析，劉進喜等［10］使用譜分析方法研究了大型LNG 船典型節點疲勞壽命。深水海洋平臺承受惡劣的風、浪、流環境載荷以及作業時的動態載荷等的作用，其中海浪的動載荷是引起疲勞的最主要因素，所以一般在海洋結構物疲勞強度研究中主要考慮海浪對疲勞損傷的作用，并且假定各個短期海況下的應力響應范圍統計符合Rayleigh 分布，其概率密度函數形式如下:

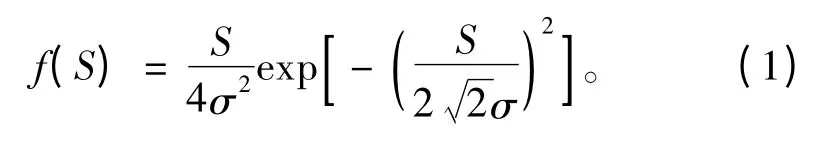
式中:S 為應力范圍;σ 為應力峰值均方差。選取中國南海波浪散布圖［11］為該半潛式海洋平臺的長期海況資料，海浪譜取JONSWAP 譜，譜峰提升因子取3.3。由波高和波浪周期表示的譜公式為

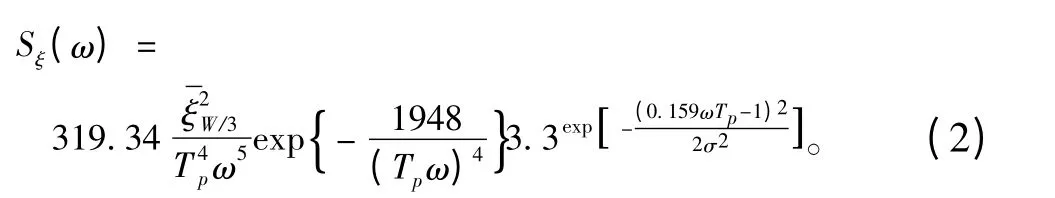
2.1 S－N 曲線計算疲勞壽命

對于特定海區作業的海洋平臺，其服役期間所遭遇海況的長期分布可由該海區的波浪散布圖確定。根據Miner 法則，總的疲勞應力參數可由各短期海況的疲勞應力參數線性疊加而得。考慮雨流修正和低應力范圍修正后，結構疲勞應力參數可表達為［12］

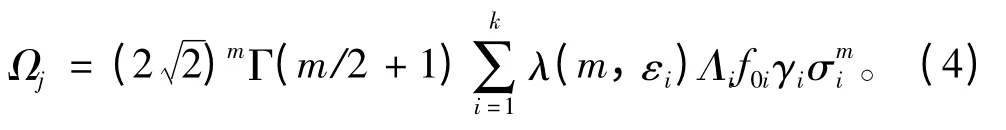
式中:Ωj為某一浪向下的應力參數，總的疲勞應力參數其中q 為總的浪向數，pj為各浪向出現概率;σi為第i 個短期海況中交變應力Rayleigh分布的均方差;Γ 為伽馬函數;f0i為各個短期海況的應力響應跨零頻率;γi為各個有義波高HS 和過零周期TZ組合(短期海況)出現的概率;k 為波浪散布圖中各短期海況總數;εi為帶寬系數;λ(m，εi)為雨流修正系數。計算雨流修正系數的經驗公式為

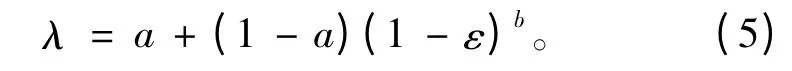
式中:a=0.926－0.033 m;b=1.587 m－2.323;m 為S－N 曲線SmN=A 的參數。Λi為考慮低應力范圍的疲勞損傷修正系數［12］。

S－N 曲線方法中的疲勞壽命計算公式為［12］

式中Δ 為疲勞累積損傷因子，一般認為達到1.0 時結構發生了疲勞破壞。

2.2 裂紋擴展模型計算疲勞壽命

在采用裂紋擴展方法計算疲勞壽命時，Paris 模型最為常用。Paris 裂紋擴展公式為

式中:C 和m 為材料的裂紋擴展參數;Y(a)為幾何修正系數;a 為裂紋長度;S 為應力范圍。

考慮低應力范圍的疲勞損傷修正后，結構的疲勞壽命為［12］

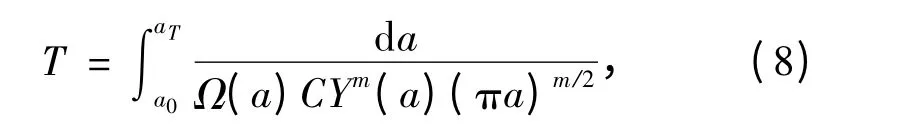
其中，與S－N 曲線方法類似有:

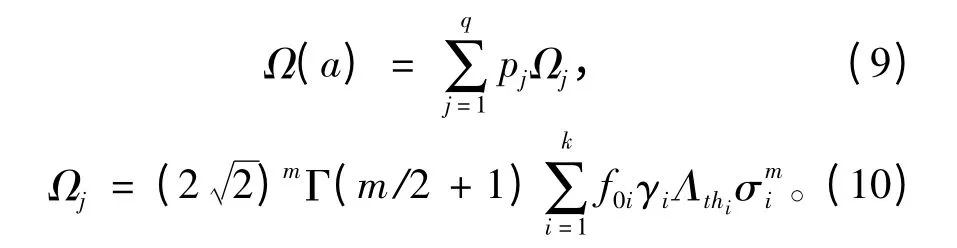
低應力范圍的門檻值修正系數Λthi與裂紋長度a有關，可表示為

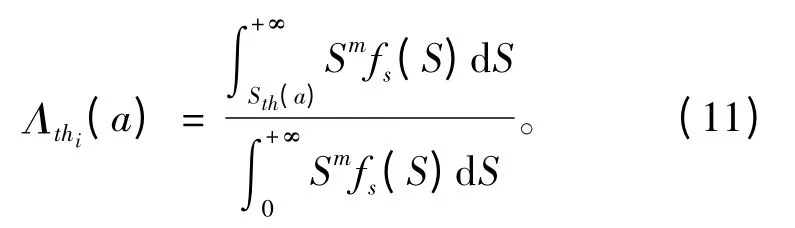
式中:Sth為應力范圍門檻值;fs(S)為應力范圍分布的概率密度函數即式(1)。

2.3 計算實例

前述半潛式海洋平臺結構疲勞分析的參數選定如下:

1)S－N 曲線

選定DNV 規范［5］中的D 曲線參數，lgA=12.116，m=3，m′=5，SQ=52.63 MPa。板厚大于25 mm 時，采用以下應力范圍修正公式

式中:S0為實際應力范圍;T 為板厚。

2)Paris 公式

選定英國BS－2005 規范［13］中的裂紋擴展參數A=5.21 ×10-13，m=3，ΔKth=2 MPa·m0.5，板厚25 mm，初始裂紋深度為0.1 mm 或0.5 mm，幾何修正系數參考文獻［14］，即Y(a)=1.0a－0.125。

以上所有參數中，長度單位均為mm，應力單位為MPa。本文假設所有浪向出現概率均等。

計算得到的疲勞壽命結果見表1 和表2，從表1中可以看出2 種評估方法計算得到的疲勞壽命較為接近。該平臺的設計壽命為30年，表1 中使用S－N 方法計算得到的結果表明A 點的疲勞壽命大于30年。

表1 初始裂紋深度為0.1 mm 時典型節點疲勞壽命Tab．1 Typical nodal fatigue life with initial crack depth 0.1 mm

表2 初始裂紋深度為0.5 mm 時典型節點疲勞壽命Tab．2 Typical nodal fatigue life with initial crack depth 0.5 mm

從表1 和表2 可以看出，使用斷裂力學方法評估結構疲勞壽命時，初始裂紋深度的選取會對疲勞壽命評估結果產生較大影響。原因在于裂紋深度較小時，裂紋擴展速率較低，隨著裂紋深度增長，裂紋擴展速率逐漸變大，因此裂紋穿透板厚的時間主要位于裂紋深度較小的擴展階段。而初始裂紋深度有很大的隨機性，與結構的類型、制造工藝、制造廠家和焊接工藝等大量因素有關，一般在0.1 ～1 mm 之間［12］，ABS 規范［4］推薦的初始裂紋在0.10 ～0.25 mm 之間，DNV 規范［5］推薦的為0.5 mm。而S－N曲線方法忽略了結構節點的初始缺陷情況，給出的是基于試驗統計的具有一定置信度的疲勞壽命評估結果。綜上所述在使用斷裂力學方法時確定初始裂紋深度顯得尤為重要，同時也說明S－N 曲線方法和斷裂力學方法在評估疲勞壽命時沒有絕對的可比性。

3 設計波法計算結構疲勞壽命

馮國慶和任慧龍［15］使用設計波法對某滾裝船的典型結構進行了疲勞壽命評估，并且給出了使用設計波法計算船體結構疲勞壽命的詳細流程，肖桃云等［16］基于設計波法對艦船整體結構進行了有限元分析，得到了全船的應力分布。李依陽［17］使用設計波法對船舶結構疲勞強度進行了評估，分別以船中處垂向波浪彎矩、水平彎矩、垂向剪力和水平剪力為設計波浪載荷對大量關鍵節點進行了疲勞壽命計算。結構疲勞分析中的設計波法主要源于如下觀點:構件的結構應力主要由某種波浪載荷主導。疲勞壽命評估中的設計波法需要選定特征設計波浪載荷類型，然后計算波浪載荷傳遞函數，選定峰值最大點所對應浪向為設計浪向，對應的頻率為設計波浪頻率以及根據長期預報極值確定相應的設計波高，因此在載荷計算分析中首先需要計算波浪載荷傳遞函數。根據ISSC［6］的建議，本文在設計波法中分別以縱垂向彎矩、橫垂向彎矩、中縱剖面的橫向扭矩和撐桿與立柱節點處水動壓力(圖1 中A 點)為設計波浪載荷類型來計算結構疲勞壽命，因此需要計算4 種波浪載荷的傳遞函數。由于該半潛平臺線型左右對稱且前后基本對稱，于是120° ～330°浪向的波浪彎矩或扭矩傳遞函數和0° ～90°的具有重復性，因此圖3、圖5 和圖6 只給出0° ～90°的波浪彎矩或扭矩傳遞函數，而水動壓力需要給出全浪向的值，計算得到的4 種傳遞函數如圖3 ～圖6所示。

一般情況下，使用設計波法計算半潛式海洋平臺結構疲勞壽命過程如下:

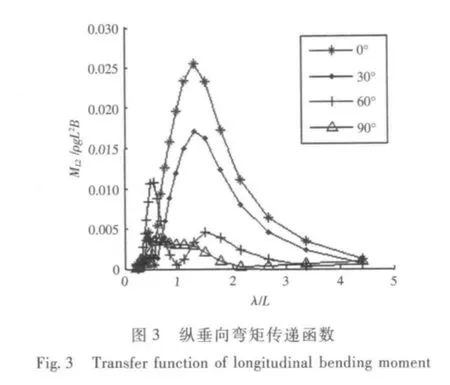
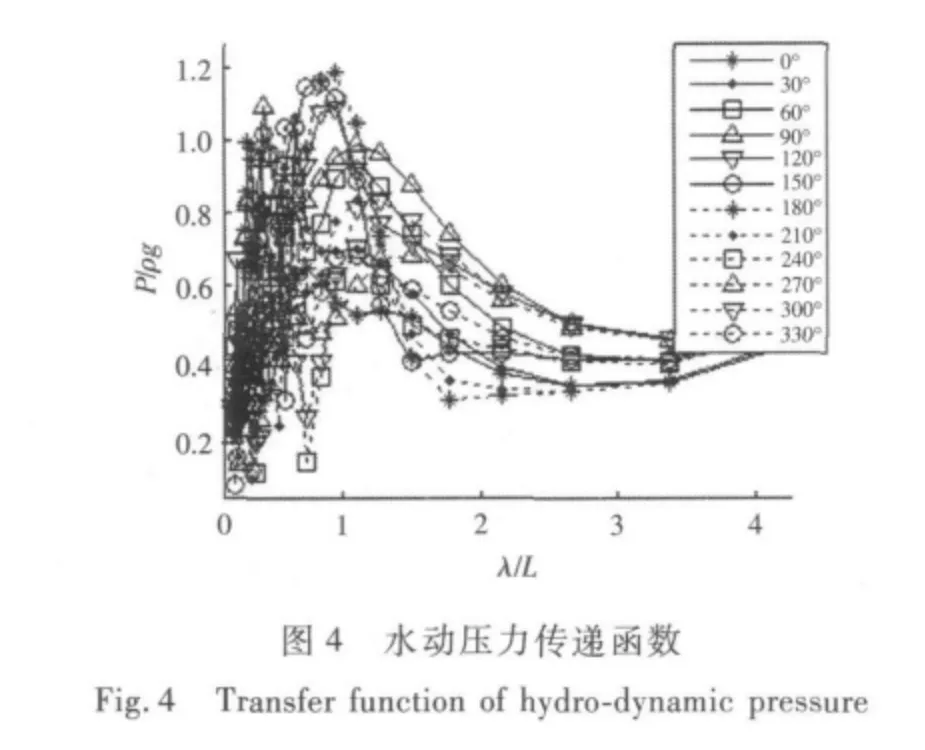
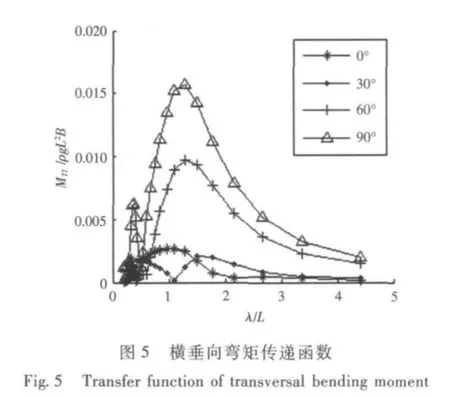
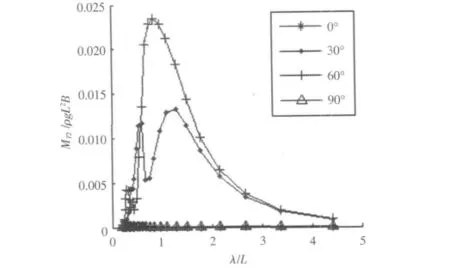
圖6 橫向扭矩傳遞函數Fig．6 Transfer function of transversal torsional moment

1)選擇典型的海況資料，本文選取中國南海波浪散布圖［11］。用三維勢流方法計算平臺在單位波幅規則波下的運動和波浪載荷傳遞函數。一般假設波浪載荷的長期分布服從Weibull 分布，然后對波浪載荷進行長期預報，取一定超越概率水平預報值作為設計值。按照ISSC［6］疲勞強度評估方法，這一概率水平取為10－4。油船和散貨船共同規范疲勞評估中也推薦取概率水平10－4。目前正在協調的共同規范建議取超越概率為10－2，認為10－2超越概率水平的載荷對結構疲勞損傷的貢獻最大，而且此時Weibull形狀參數對疲勞壽命評估結果影響較小。但是本文認為對結構疲勞損傷的貢獻率最大的超越概率不一定為10－2，這與形狀參數和S－N 曲線的反斜率m有關。同時本文不認同10－2超越概率水平下，Weibull 形狀參數對疲勞壽命評估結果影響最小的觀點。基于以上分析，本文選取的超越概率水平為10－4。

2)設計波的浪向和頻率根據設計波浪載荷的傳遞函數最大值決定。

3)設計波波幅等于設計波浪載荷的長期預報值除以對應傳遞函數的最大值。

4)對平臺施加設計波浪向、頻率和單位波幅下的波浪載荷，計算熱點應力。

5)同等超越概率水平下的應力范圍設計值為設計波波高乘上單位波幅下的熱點應力。

6)假設平臺結構應力范圍長期分布服從Weibull 分布，其形狀參數取波浪載荷長期預報結果所服從的Weibull 分布的形狀參數。根據熱點應力范圍設計值和超越概率水平可以得到應力范圍長期分布的Weibull 尺度參數，從而平臺結構應力范圍長期分布完全確定。

7)得到應力范圍的長期Weibull 分布后，就可以通過式(13)計算等效應力［12］，然后使用S－N 曲線方法或斷裂力學方法進行疲勞壽命評估。

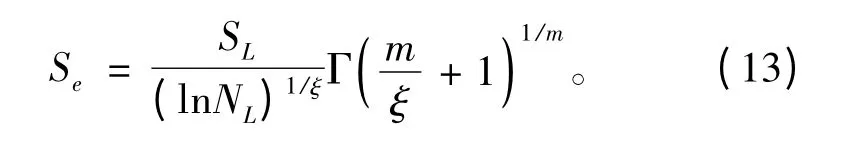
式中:m 為S－N 曲線參數;ξ 為Weibull 分布的形狀參數;SL為熱點應力范圍設計值即步驟5 的計算結果;NL為循環次數。

按照上述步驟計算得到不同設計波載荷類型下的設計波長、浪向、波高和Weibull 形狀參數如表3所示，表4 給出了不同設計波參數下的熱點應力幅值。

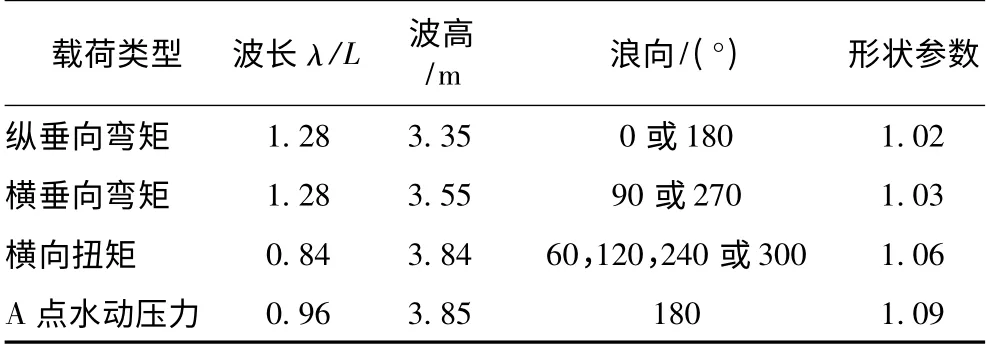
表3 設計波參數Tab．3 Design wave parameters

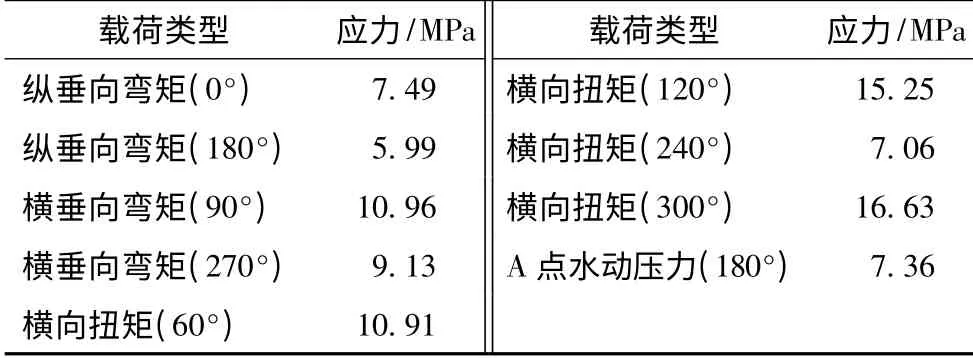
表4 熱點應力幅值Tab．4 Stress amplitude in hotspot

根據表3 中的設計波參數，使用S－N 曲線方法分別計算得到節點的疲勞壽命見表5，使用斷裂力學的Paris 方法分別計算得到節點的疲勞壽命見表6。從表5 和表6 可以看出以橫向扭矩(60°)為設計波浪載荷，計算得到的疲勞壽命和表1 中使用S－N 曲線方法或Paris 方法計算得到的結果較為接近，可能原因在于橫向扭矩對A 點的應力影響大。因此本文認為在使用設計波法計算半潛式平臺撐桿和立柱交界處節點疲勞壽命時，設計波浪載荷類型應該選用橫向扭矩(60°)。從表5 和表6 的計算結果還可以發現，即使對同樣的載荷類型，不同浪向下的結構疲勞壽命計算結果也存在很大的差別，這是因為不同浪向下結構關鍵節點的熱點應力響應差別較大(見表4)。例如縱垂向彎矩分別在0°與180°浪向計算得到的疲勞壽命，橫垂向彎矩在90°與270°計算得到的疲勞壽命均差別較大。這可從波浪載荷的勢流理論上進行解釋，即針對平臺上某一結構位置來說，相對浪向的波浪入射勢和輻射勢是相同的，而繞射勢不同，這樣在該點造成的結構應力也將不同。

從力學角度出發可以發現，橫垂向彎矩主要使A 點局部結構產生彎矩應力，而橫向扭矩主要使A點產生薄膜應力，對A 點來說橫向扭矩導致的薄膜應力會大于橫垂向彎矩引起的彎矩應力。雖然縱垂向彎矩也是使A 點局部結構產生總縱薄膜應力，但是由于A 點遠離平臺中橫剖面，因此縱垂向彎矩引起的總縱薄膜應力應該較小。而局部水動壓力使該處產生彎矩應力，其引起的彎矩應力較小。

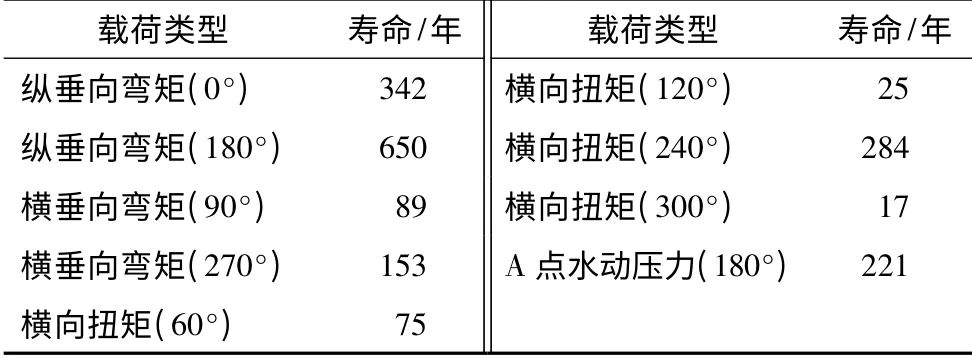
表5 S－N 曲線計算的疲勞壽命Tab．5 Fatigue life in S－N curve method

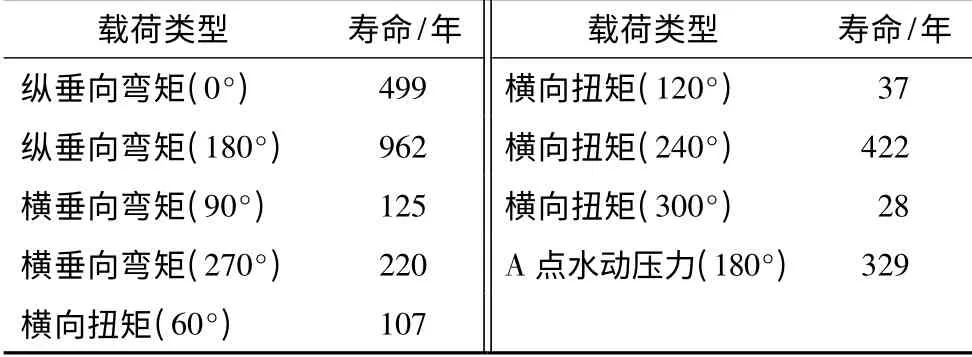
表6 Paris 公式計算的疲勞壽命(初始裂紋長度0.1 mm)Tab．6 Fatigue life in Paris method with initial crack depth 0.1 mm

4 結 語

為了探討船舶與海洋工程結構物疲勞強度分析中各種評估分析方法對疲勞壽命的影響，本文從疲勞載荷和疲勞損傷模式兩方面對幾種主要的疲勞壽命評估方法進行了比較分析。

采用S－N 曲線方法和Paris 斷裂力學方法分別計算了某半潛式海洋平臺典型節點疲勞壽命，經過比較分析后認為這2 種方法的計算結果較為接近，應用于評估半潛式海洋平臺疲勞壽命均是可行的。同時發現裂紋擴展理論中，初始裂紋長度對最終的疲勞壽命評估影響較大。

通過波浪載荷的譜分析方法和設計波法分別進行了半潛式海洋平臺撐桿和立柱交界處典型節點的疲勞壽命評估。比較譜分析方法和設計波法的計算結果后，發現設計波法中應以60°浪向的橫向扭矩為設計波浪載荷來確定設計波參數。

今后尚需對半潛式海洋平臺其他位置處的典型節點進行評估分析，以獲得更具普遍性的分析結論。

［1］崔維成，等．船舶結構疲勞強度校核研究現狀及我國的發展［J］．船舶力學，1998，2(4):63－81．

CUI Wei-cheng，et al．A state-of-the-art review for the fatigue strength assessment of ship structures［J］．Journal of Ship Mechanics 1998，1(4):63－81．

［2］XU T．Fatigue of ship structure details-technical development and problems［J］．Journal of Ship Research，1997，14(4):318－331．

［3］FRICKE W，CUI W C．Comparative fatigue strength assessment of a structure detail in a containership using various approaches of classification societies［J］．Marine Structures，2002，115:1－13．

［4］ABS．Fatigue assessment of offshore structures［S］．2003．

［5］DNV．Fatigue design of offshore steel structures［S］．2005．

［6］ISSC．Fatigue loading (COMMITTEE VI．1)［C］．Proceedings of 15 th International Ship and Offshore Structures Congress，San Diego，USA．2003．

［7］戴仰山，沈進威，宋競正．船舶波浪載荷［M］．北京:國防工業出版社，2006．

［8］馮國慶．船舶結構疲勞強度評估方法研究［D］．哈爾濱:哈爾濱工程大學，2006．

［9］馬網扣，王志青，張海彬．深水半潛式鉆井平臺節點疲勞壽命譜分析研究［J］．海洋工程，2008，26(3):1－8．

MA Wang-kou，WANG Zhi-qing，ZHANG Hai-bin．Study on spectrum-based fatigue life direct calculation for spots of deep-water semi-submerged drilling unit［J］．The Ocean Engineering，2008，26(3):1－8．

［10］劉進喜，唐永生，樓丹平，趙耀，葉恒奎．大型LNG 船典型節點疲勞壽命譜分析評估［J］．海洋工程，2010，28(3):86－90．

LIU Jing-xi，TANG Yong-sheng，LOU Dan-ping，ZHAO Yao，YE Heng-kui．Fatigue strength assessment of typical spots in a large LNGC based on spectral method［J］．The Ocean Engineering，2010，28(3):86－90．

［11］HOBGEN N，DACUNBA L F，OLLIVER H N．Global wave statistics(GWS)［M］．Brown Union Pub．，London，1986．

［12］胡毓仁，李典慶，陳伯真．船舶與海洋工程結構疲勞可靠性分析［M］．哈爾濱:哈爾濱工程大學出版社，2010．

［13］BS7910．Guide to methods for assessing the acceptability of flaws in metallic structures［S］．2005:57．

［14］KUNG C J，WIRSCHING P H．Fatigue and fracture reliability and maintainability of TLP tendons［J］．OMAE，Safety and Reliability，ASME 1992，II:15－21．

［15］馮國慶，任慧龍．船體結構疲勞評估的設計波法［J］．哈爾濱工程大學學報，2005，26(4):430－434．

FENG Guo-qing，REN Hui-long．Design wave approach for the fatigue assessment of ship structures［J］．Journal of Harbin Engineering University，2005，26(4):430－434．

［16］肖桃云，樊佳，梅國輝，侯國祥，陳力，張聰，胡奔．基于設計波法的艦船整船有限元強度分析［J］．艦船科學技術，2010，32(6):37－43．

XIAO Tao-yun，FAN Jia，MEI Guo-hui，et al．Strength analysis of overall ship FEM model based on design wave approach［J］．Ship Science and Technology，2010，32(6):14－19．

［17］李依陽．船舶結構疲勞強度評估的設計波法［D］．哈爾濱:哈爾濱工程大學，2010．