非接觸機械密封的非線性動特性系數及瞬態振動響應分析
王技德 張國淵
1.蘭州職業技術學院,蘭州,730070 2.西北工業大學,西安,710072
0 引言
非接觸密封作為重要裝備的關鍵基礎件,被廣泛應用在航空航天、能源環境、石油化工等領域(如石化泵、渦輪泵及核泵等)中[1-4]。在一些極端工況條件下,由于軸向振動過大或者受到瞬態沖擊,機械密封經常會出現變形或者密封副表面損壞等,這些現象極易引起密封的失效[2,5-6]。考慮瞬態過程非線性因素的振動特性研究正成為非接觸式機械密封設計和研究中的一個重要內容[3],這對機械密封可靠、穩定地運行有著舉足輕重的作用,因此對機械密封瞬態快速啟動過程的響應特性進行研究就變得更為重要。然而已有的研究大多是采用商用軟件對密封模型進行流固耦合下的穩態性能分析,主要是對其靜態潤滑特性進行分析,如研究密封的膜厚變化、平均溫升、熱變形等,對振動響應研究較少。張國淵等[1,2,7]對非接觸機械密封瞬態啟動過程中脫開轉速和密封可控性進行了研究,分析了密封的靜態潤滑特性和密封效應;Brunetière等[4,8]研究了密封的穩態熱動力模型及穩態熱效應;王之櫟等[5]、張偉政等[9]研究了氣膜密封因外界擾動而引起的振動和角向擺動對密封動態特性的影響;賀立峰等[6]分析了彈簧剛度改變對端面接觸式機械密封振動的影響;丁雪興等[10]對螺旋槽干氣密封系統非線性動力學行為進行了研究。然而,上述研究都未對密封考慮擺動時的非線性相關的動態特性系數進行研究,對其瞬態過程的振動特性的研究也很少。為此,本文提出考慮傾斜情況的彈性補償單元支撐的包含Reynolds方程、運動方程等的非接觸機械密封瞬態非線性振動分析模型,并以此研究受外部軸向沖擊載荷時密封的振動響應以及響應過程中密封的非線性軸向力、剛度和阻尼系數的響應特征。
1 瞬態非線性振動響應模型
1.1 瞬態Reynolds方程
本文研究的非接觸機械密封結構見圖1,它依靠在密封端面間形成的微小間隙(流體膜)實現密封副的非接觸密封,其密封機理是,允許微小的在可控制范圍內的流體泄漏,但保證密封的長壽命、高可靠性以及密封良好的外部軸向小振動的跟隨性。

圖1 非接觸機械密封示意圖
根據流體力學中的N-S方程和連續性方程,在相應的假設條件下可得到柱坐標(r,θ)下的量綱一 Reynolds方程[11]:
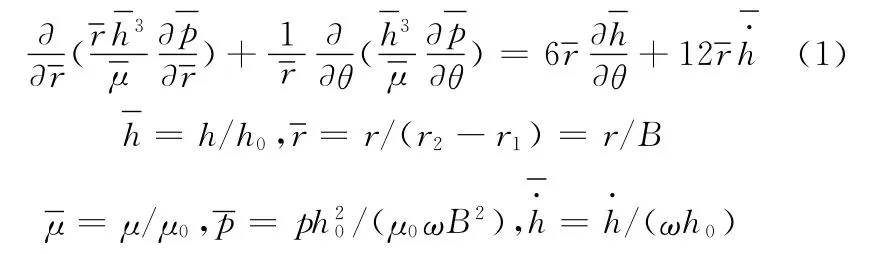
式中,r1、r2、B 分別為密封環外徑、內徑和徑向長度;h、h0分別為瞬態、穩態時油膜厚度;μ0為初始動力黏度;ω為轉速 ;p 為 油 膜 壓 力 值 ,h·為油膜的擠壓速度。
量綱一邊界條件為
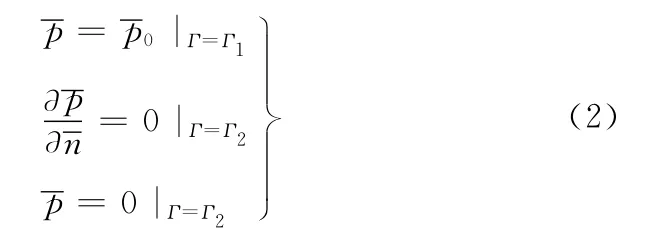
其中,p0為邊界壓力值;n為法線方向;Γ1表示密封的介質入口,Γ2表示除Γ1外的其他邊界,Γ表示全部邊界。
1.2 瞬態運動方程
根據Newton力學第二定律,可以建立動環和靜環配對的動力學方程和靜環力矩平衡方程如下:
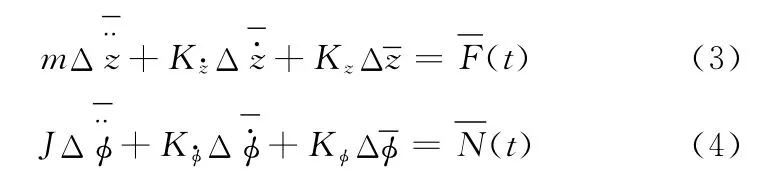
式中,z為密封環軸向運動量;m為密封環的質量;Kz、Kz·分別為油膜對密封環的力剛度與阻尼系數;F(t)為外部軸向載荷變化量(穩態時,F(t)=0);J為密封環的轉動慣量;Kφ、Kφ·分別為油膜對密封環的力矩剛度和阻尼系數;φ為傾斜靜環的傾角;N(t)為油膜對密封環的外力矩(傾覆力矩)。
從式(3)、式(4)可以看出,密封環的軸向運動與其傾斜擺動無關。實際上并非如此,密封副振動影響油膜厚度分布,從而使油膜壓力分布發生變化,結果導致產生傾覆力矩而使得密封環擺動。同樣,密封環擺動也會引起軸向振動,這可以從下面的分析看到,然而線性分析是無法了解密封環運動與擺動之間的關系的。
1.3 考慮密封環傾斜的密封間隙方程和軸向載荷
密封間隙控制方程為
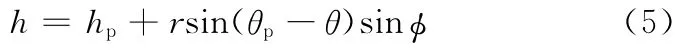
式中,hp為彈性補償單元作用支點處的油膜厚度;θp為密封傾斜節線的周向角。
對密封間隙內油膜承載區域的壓力進行積分,可得到油膜軸向承載力公式:
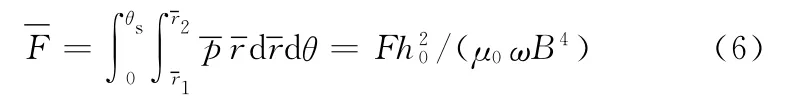
式中,F為承載力;θs為油膜邊界值。
非接觸機械密封正常工作過程中,由油膜產生的軸向承載力即為密封開啟力,密封的閉合力由彈簧等補償單元的彈性補償力和密封腔內作用在密封環的介質壓力構成,這些力構成的閉合力和開啟力的大小相等、方向相反。
對于考慮密封環傾斜的機械密封,還必須考慮其傾覆力矩:
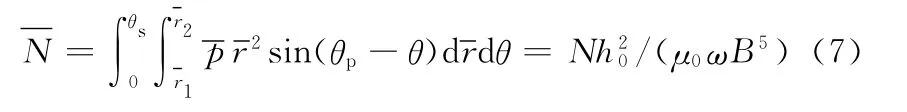
1.4 二階非線性動特性求解模型
1.4.1 密封間隙的油膜厚度二階級數
油膜厚度在擾動下的方程為
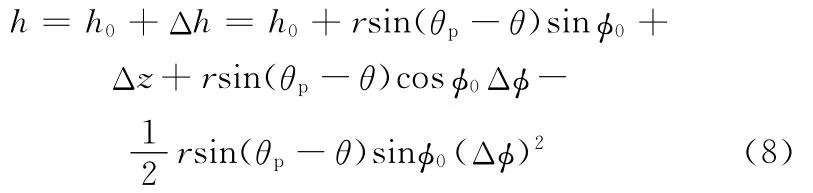
式中,φ0為穩態下的密封靜環傾角;Δz為h0沿軸向的增量;Δφ為φ0沿周向的增量。
在瞬態下有

1.4.2 密封開啟力及傾覆力矩的二階級數
靜態開啟力為F0時,瞬態下密封間隙內油膜對密封副的作用力矩陣形式為
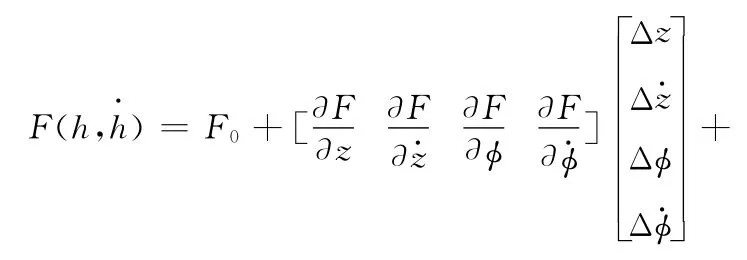

瞬態下油膜對傾覆力矩的矩陣形式為
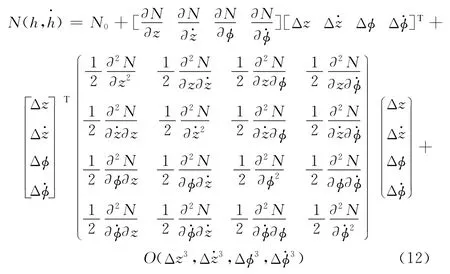
1.4.3 二階非線性動特性系數
靜態傾覆力矩為N0時,瞬態下油膜對密封的開啟力用剛度阻尼系數的矩陣形式表示為
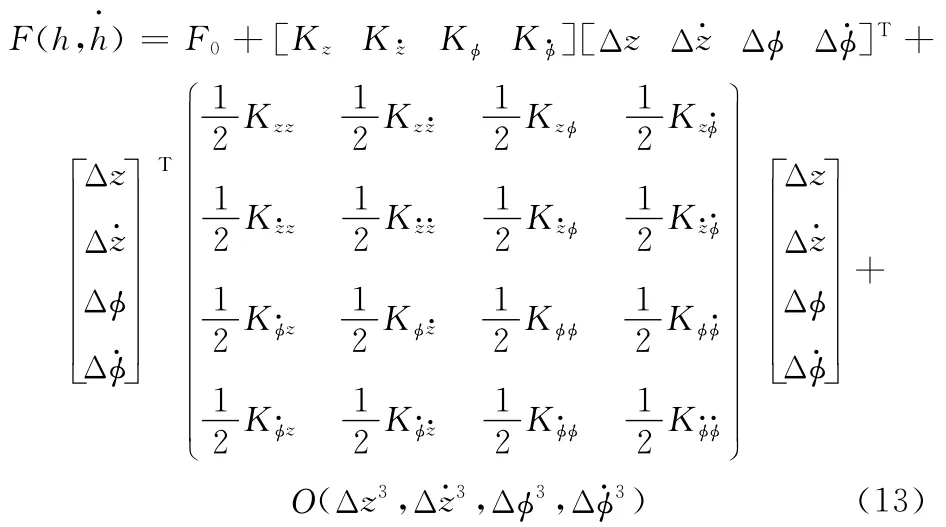
其中,K 為力剛度阻尼參數,下標z、φ、z·、φ·分別表示沿軸向、周向的位移和速度項。
由式(6)、式(11)、式(13)可得到瞬態下油膜對密封環的作用力的非線性動力學系數,其中線性剛度系數為(P為量綱一壓力)
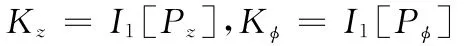
線性阻尼系數為
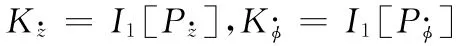
二階非線性主剛度和交叉剛度系數為
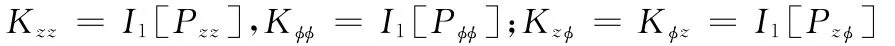
二階非線性主阻尼和交叉阻尼系數為
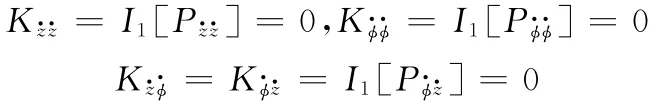
非線性剛度阻尼耦合系數為
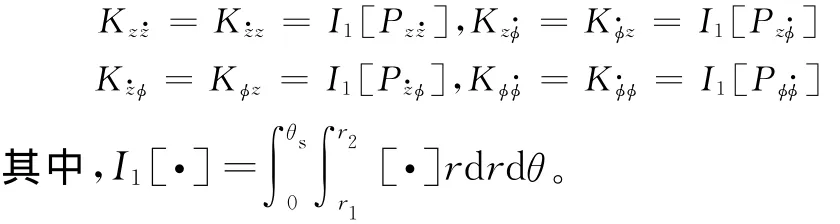
瞬態下油膜引起的傾覆力矩用擺動剛度阻尼系數表示的矩陣形式為(V為擺動剛度阻尼系數的統一標示量):
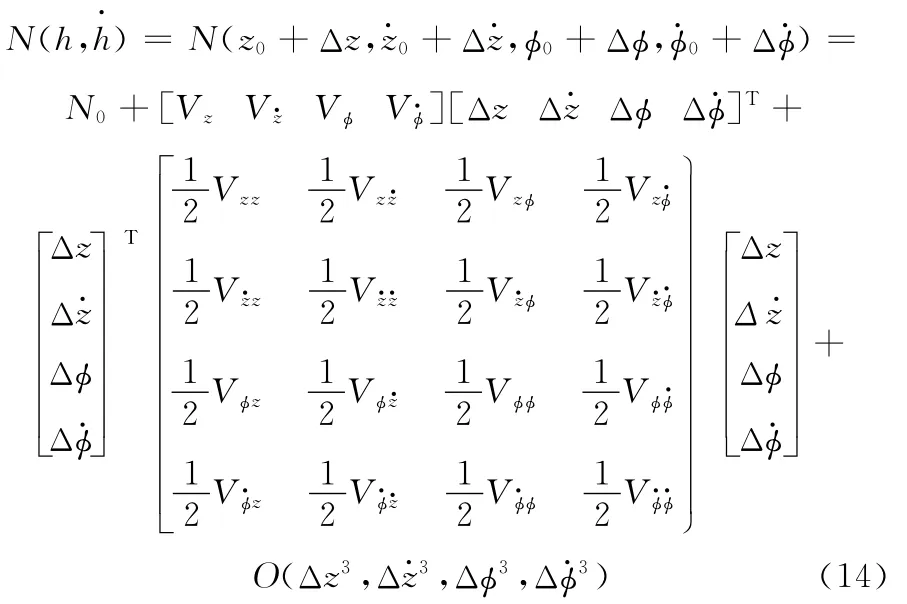
由式(7)、式(12)、式(14)可得到油膜對傾覆力矩的線性及非線性動力學系數,其中線性剛度系數為
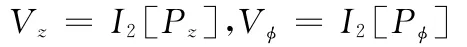
線性阻尼系數為
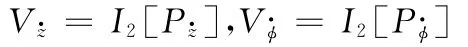
二階非線性剛度系數為
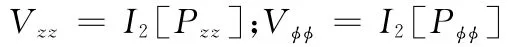
二階非線性交叉剛度系數為
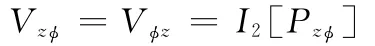
二階非線性阻尼系數為
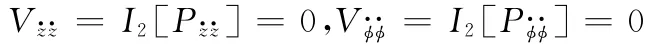
二階非線性交叉阻尼系數為
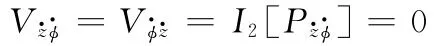
二階非線性剛度阻尼耦合系數為
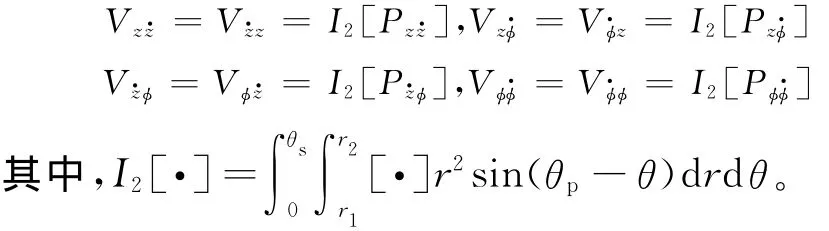
由式(13)和式(14)知,瞬態油膜作用時,與密封副軸向力和傾覆力矩相關的動特性系數各有20個,由于式(13)和式(14)中矩陣是對稱的,因此分別包含14個動特性系數。
從推導中知:
(1)非線性阻尼系數均等于0,這說明油膜阻尼對密封副和擺動的影響是線性的,這是由于瞬態Reynolds方程中瞬態項?h/?t是一階的緣故。
(2)密封副振動影響油膜厚度分布,從而使油膜壓力分布發生變化,導致密封環擺動;同樣,密封副擺動也會引起密封軸向振動。
1.4.4 瞬態運動方程
考慮密封環的慣性時,將剛度阻尼代入式(5)和式(6)后,密封環的二階非線性量綱一軸向振動方程為
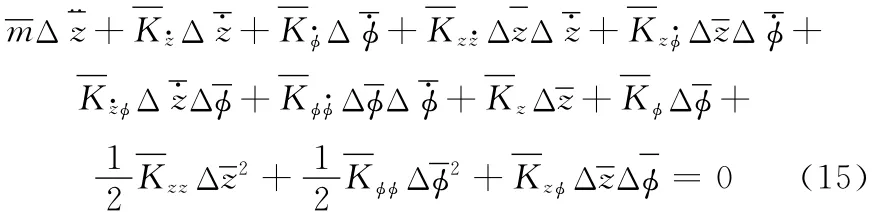
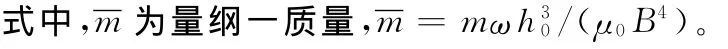
擺動下的二階非線性量綱一運動方程為
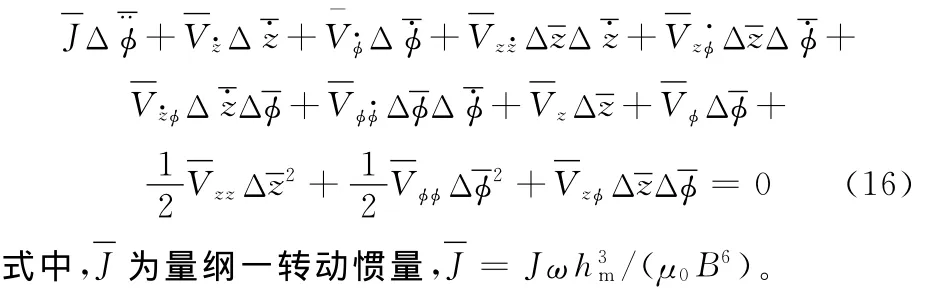
2 算例分析
2.1 計算對象和剛度阻尼計算結果分析
計算對象機械密封的幾何參數如下:r1=0.125m,r2=0.21m,θs=0.452rad,θp=0.265rad;被密封介質溫度t=40℃,μ0=0.04315Pa·s,密度998kg/m3。密封運行條件:ω=3500r/min,軸向載荷W =1.8×105N。
在已有程序基礎上[1,7,12],引入式(8)~ 式(14),編制程序并計算,獲得的非線性動特性系數的量綱一數值如表1所示。
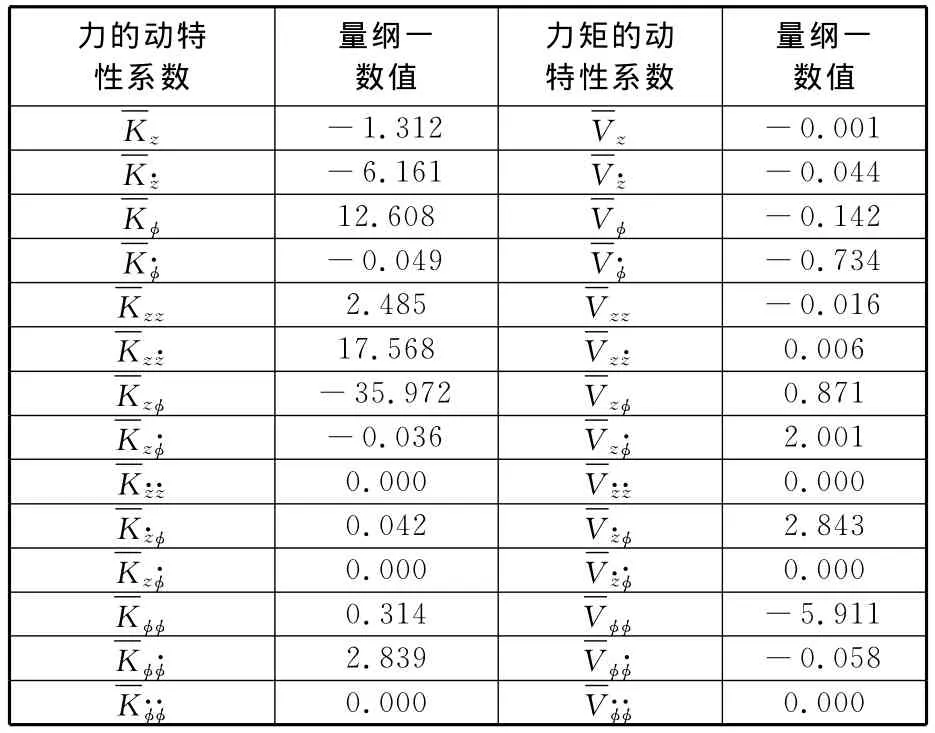
表1 動特性系數的量綱一數值
2.2 密封瞬態振動響應過程計算結果分析


圖2 軸向振動響應(=0.3,=0)
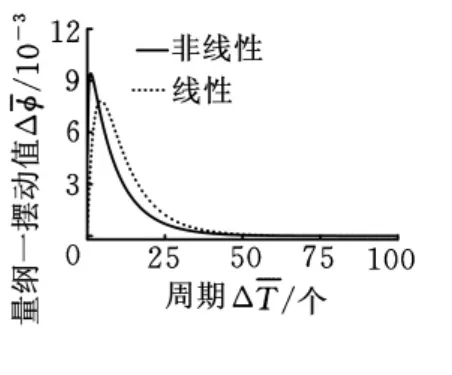
圖3 擺動響應(=0.3,=0)
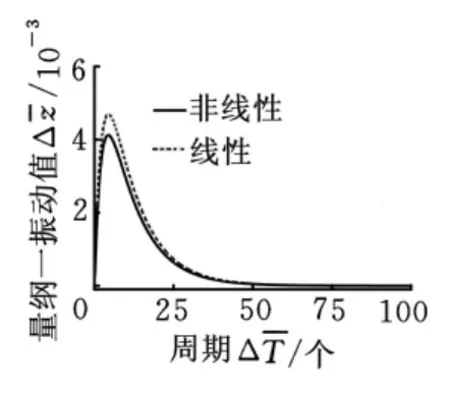
圖4 軸向振動響應(=0,=1.0×10-3)
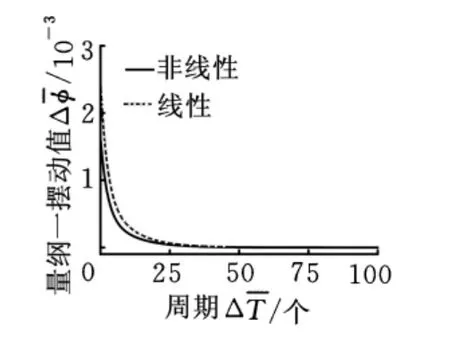
圖5 擺動響應(=0,=1.0×10-3)
3 結論
(1)建立了考慮傾斜情況的彈性補償單元支撐的非接觸機械密封瞬態振動響應分析模型,該模型包括了瞬態Reynolds方程、運動方程以及二階非線性動特性求解方程等。(2)通過Euler法求解獲得了非接觸機械密封在軸向振動位移和靜環傾角隨時間變化時的瞬態振動響應特性。(3)計算得到了瞬態油膜對密封副作用力和傾覆力矩的各14個動特性系數,結果表明:油膜阻尼對密封副和擺動的影響是線性的;密封的副振動影響油膜厚度分布,從而引起油膜壓力分布發生變化,導致密封環擺動;密封副擺動同樣也會引起密封軸向振動。
[1]Zhang G Y,Zhao W G,Yan X T,et al.Theoretical and Experimental Study on Characteristics of Water-lubricated Double Spiral Grooved Seals[J].Tribology Transactions,2011,54(3):362-369.
[2]張國淵,趙偉剛,閆秀天,等.可控式液體潤滑高速螺旋槽端面密封試驗研究[J].航空動力學報,2010,26(4):947-953.
[3]彭旭東,王玉明,黃興,等.密封技術的現狀與發展趨勢[J].液壓氣動與密封,2009(4):4-11.
[4]Brunetière N,Galenne E,Tournerie B,et al.Modelling of Non-laminar Phenomena in High Reliability Hydrostatic Seals Operating in Extreme Conditions[J].Tribology International,2008,41(4):211-220.
[5]王之櫟,劉國西,郭艷麗.反轉軸間氣膜密封振動過程分析[J].振動與沖擊,2011,30(2):181-185.
[6]賀立峰,朱漢華,范世東,等.彈簧剛度對端面接觸式機械密封振動的影響[J].潤滑與密封,2010,36(6):64-68.
[7]張國淵,袁小陽,趙偉剛,等.螺旋槽端面密封脫開轉速的理論及實驗研究[J].機械工程學報,2008,44(8):55-60.
[8]Brunetière N,Apostolescu A.A Simple Approach to the ThermoElastoHydroDynamic Behavior of Mechanical Face Seals[J].Tribology Transactions,2009,52(2):243-255.
[9]張偉政,俞樹榮,丁雪興,等.干氣密封系統角向擺動的穩定性及其振動響應[J].振動與沖擊,2011,30(3):96-99.
[10]丁雪興,張偉政,俞樹榮,等.螺旋槽干氣密封系統非線性動力學行為分析[J].中國機械工程,2010,21(9):1083-1087.
[11]平克斯·O,斯德因李希特·B.流體動力潤滑理論[M].西安交通大學軸承研究小組,譯.北京:機械工業出版社,1980.
[12]李治國,張國淵,袁小陽,等.流體動靜壓端面密封的靜動特性分析[J].中國機械工程,2006,17(5):457-460.

