基于時間序列電流偏差因子的電源－電弧系統穩定性研究

李春天 杜長華 許惠斌 羅 怡

重慶理工大學，重慶，400054

0 引言

在電弧焊過程中，焊接電源作為供電提供者為電弧提供能量，而電弧是電弧焊接的熱源，作為供電對象，電弧消耗能量以保持連續燃燒，構成電源—電弧系統。在這個系統中，弧焊電源外特性影響電弧燃燒的穩定性，而電弧是否穩定燃燒又直接影響焊接工藝參數的穩定性，最終影響焊縫質量，即電源－電弧系統的穩定性決定焊接質量水平的高低。

1 電源－電弧系統穩定性的量化模型［1］

圖1為電源－電弧系統示意圖。電源－電弧系統穩定性的內涵包括兩個方面：一方面，系統在無外界因素干擾時能夠保證電弧在給定工藝電壓與電流下維持連續放電并穩定燃燒，保持系統的靜態平衡，這是系統最理想的目標性穩定平衡；另一方面，在實際焊接過程中，系統不可避免地受外界因素干擾，諸如工件焊區表面的凸凹不平、操作的不穩定、送絲速度的較小變化、電網電壓的波動等因素，會破壞系統的靜態平衡，這就要求系統在外界干擾因素消失后，能自動恢復或達到新的靜態平衡，使得焊接工藝參數重新得以恢復并保持穩定［2－3］。

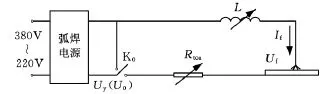
圖1 電源－電弧系統示意圖

1.1 系統的靜態模型

系統無外界因素干擾時能保證電弧在給定焊接工藝參數下連續穩定燃燒，保持系統的靜態平衡，系統的電特性應有如下關系：

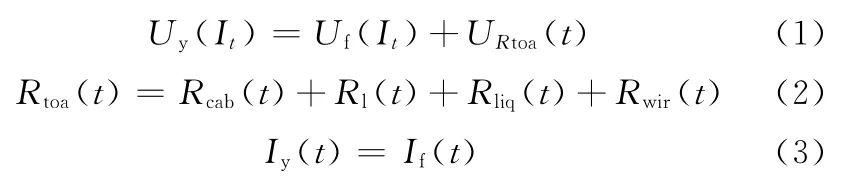
式中，Uy、Iy分別為焊接電源輸出電壓與電流的穩定值；URtoa為焊接電源外回路的電阻總電壓；Uf、If分別為電弧電壓與電流的穩定值；Rtoa為焊接電源外回路的總電阻；Rcab、Rl、Rliq、Rwir分別為電纜、電感、液態熔滴、焊絲（條）的等效電阻［4］。

電源－電弧系統工作狀態如圖2所示，曲線1、2分別為電源的外特性曲線和電弧的伏安特性曲線，兩曲線交點A0對應的電流與電壓分別為Ify、Ufy，Iwd為 穩 態 短 路 電 流，U0為 電 源 空 載 電壓，點A1、B1分別為電源和電弧的靜態工作點［3-4］。

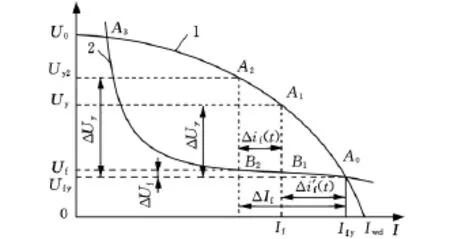
圖2 電源－電弧系統工作狀態圖

1.2 系統的動態模型

在實際焊接過程中，系統會受到外界因素的干擾，因而電源輸出電流Iy（t）與輸出電壓Uy（It）以及電弧電流If（t）與電弧電壓Uf（It）等都會發生變化，系統的動態平衡方程為

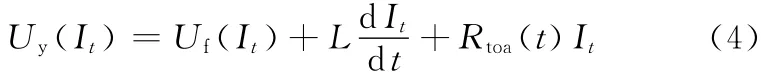
式中，It為系統每個瞬間的焊接電流；L為電感。

每一時刻的焊接電流可以采用靜態焊接電流If與相對電流偏差Δif（t）之和加以描述：

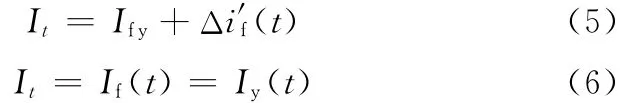
式中，Δi′f（t）為t時刻相對于A0點對應的Ify的焊接電流偏差值［5-6］。

聯立式（4）、式（5），系統的動態平衡方程又可轉化為

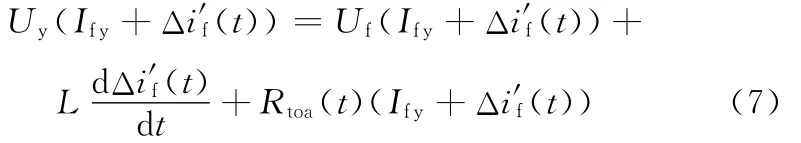
1.3 系統的穩定系數與動態電流偏差因子Δi′f（t）模型

基于微分思想，由于在 Δi′f（t）不大的范圍內（一般為－10～10A），外特性曲線1與電弧靜特性曲線2在點A0附近區域內可各自看成微小線性直線，并且與點A0的各自切線重合，則有

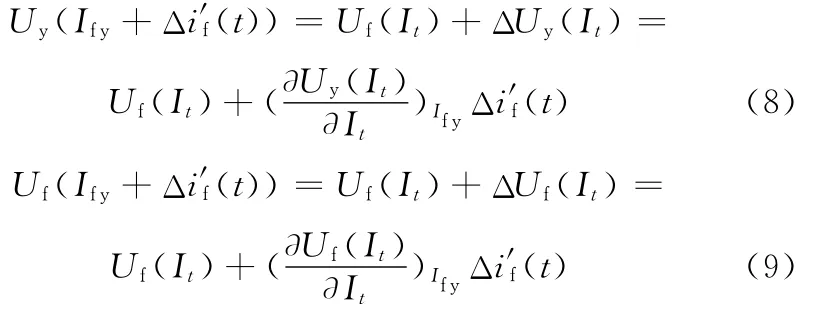
聯立式（7）～ 式（9）得

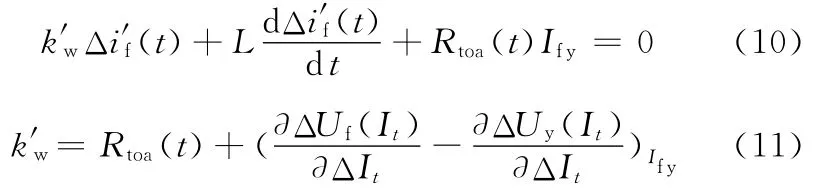
式中，k′w為系統的穩定系數。

令

這里，If為靜態平衡的焊接電流，即設定的焊接工藝規范參數；Δif（t）為相對于靜態焊接電流的每個瞬時的電流偏差值，即相對于焊接工藝規范參數的實際動態電流偏差，如圖2所示。

通過電流偏差的相對轉換，聯立式（5）、式（12），然后代入式（10）中，并考慮初始條件t＝0時，Δif（t）＝ΔIf＝max（Δif（t）），解一階微分方程式（10），得Δif（t）的動態量化方程：

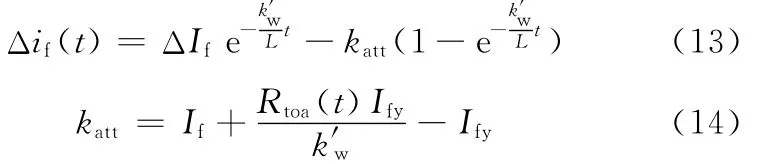
式中，ΔIf為外在因素干擾時產生的實際電流偏差最大值；katt為實際電流偏差衰減子系數。

令Δif（t）＝0，代入式（13），即得到系統使實際動態電流偏差Δif（t）衰減為零時所需的時間：

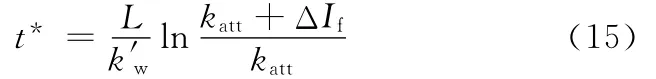
2 系統穩定性的定性與量化分析

2.1 系統穩定性的理論分析

根據式（13），由于L總是正值，要使Δif（t）在干擾消失后隨著時間推移不斷減少，直至誤差消除即其值為零，則必須使k′w＞0，故電源－電弧系統穩定的基本條件為k′w＞0。k′w正值越大，Δif（t）衰減消失的速度越快，衰減為零需要的時間t＊越小，系統穩定性越好。依據式（11），若

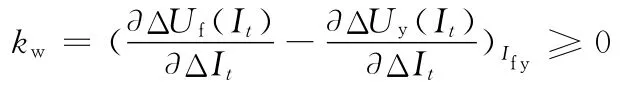
則k′w＞0，因此，電源－電弧系統穩定的最優條件為kw＞0，即在電源外特性曲線與電弧伏安特性曲線的交點A0處，電弧伏安特性曲線的斜率要大于電源外特性曲線的斜率。

Δif（t）衰減為零需要的時間t＊主要取決于Rtoa（t）、kw、katt、ΔIf、L。Δif（t）衰減過程對應的曲線如圖3所示，一方面，在其他因素不變的情況下，隨著Rtoa（t）增大，kw增大或兩者同時增大而使k′w增大，t＊減小；隨著If增大，katt增大，t＊減小；當Rtoa（t）＞k′w時，隨著Ify增大，katt增大，t＊減小；當Rtoa（t）＜k′w時，隨著Ify減小，katt增大，t＊減小。上述情況都會使t＊減小，對應的衰減曲線由2變為1，電源－電弧系統的穩定性提高率esta為

式中，S2為圖3中陰影區域面積，S1為圖3中空白區域面積。

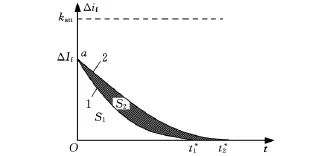
圖3 Δi′f（t）衰減曲線

在其他因素不變的情況下，若產生的ΔIf較大，則t＊相對增大，但此種情況一般不影響系統穩定性；L減小，t＊減小，系統穩定性得以提高，但L又不能太小，否則，電弧不能連續燃燒，穩定性變差。

2.2 系統穩定性的實驗分析［7］

實驗條件：焊絲牌號ER－50－6；焊絲直徑d＝1.2mm；電感L＝120μH；焊接電流If＝250A；焊接電壓Uy＝34.5V；焊接速度為42cm／min；送絲速度約為3.85m／min；焊炬高度為15mm；CO2氣流量為12L／min；焊機型號為Panasonic KRII－350，采用弧焊過程智能檢測系統［8］。

實驗中，圖4a、圖5a對應的外電路總電阻為Rtoa（t），圖4b、圖5b對應的外電路總電阻為R′toa（t），且Rtoa（t）＞R′toa（t），其余實驗條件都一致。從焊接電流波形上看，圖4a波形波動較小，說明外界干擾因素造成的電流誤差衰減的速度快，誤差消除所需的時間少，體現在波形非規律畸變非常弱，說明較大的Rtoa（t）對應的系統穩定性較強；反觀圖4b，對應的系統穩定性較差。從電弧電壓波形上看，圖5b波形波動較大，且波峰波谷峰值較大，間隔出現頻率也高，這說明由于外界干擾因素造成的電流誤差衰減的速度慢，誤差消除所需的時間長，體現在波形正常畸變大且比較頻繁，這說明較小的R′toa（t）對應的系統穩定性較差［9-10］。

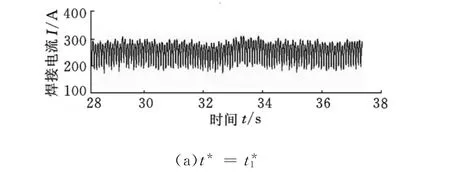
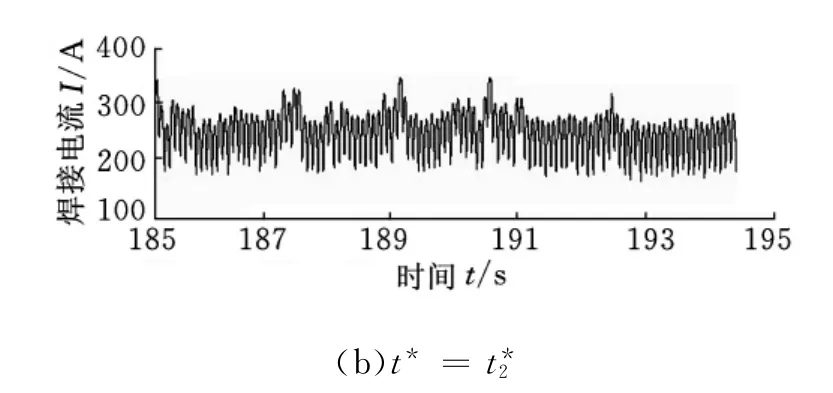
圖4 焊接電流動態波形圖（t＊1＜t＊2）

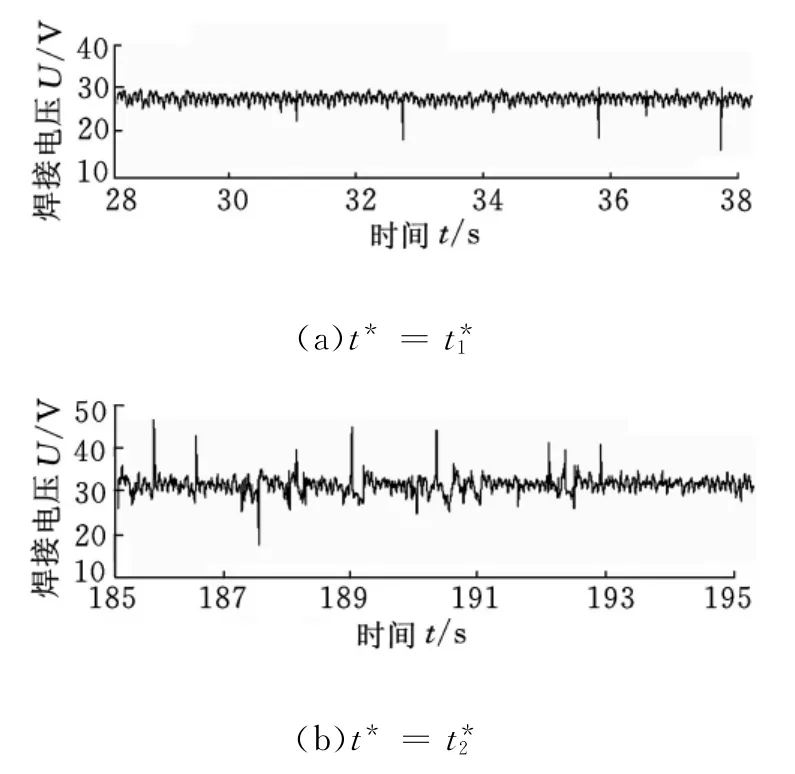
圖5 焊接電壓動態波形圖（t＊1＜t＊2）

3 結論

（1）依據電源－電弧系統靜動態模型，推導出系統穩定系數k′w的表達式，提出了系統穩定的基本條件與最優條件，定性分析了系統的穩定性。

（2）采用誤差相對轉換方法，建立了動態焊接電流偏差因子 Δif（t）模型，分析了影響 Δif（t）衰減因素與衰減時間的關系。通過k′w和實際電流偏差衰減子系數katt，刻畫了Δif（t）衰減時間t∈［0，t＊］，進而通過t＊量化了系統的穩定性。

（3）實驗結果表明，相比t＊2，較小的t＊1能使系統的穩定性相對提高。

［1］黃石生.弧焊電源與數字控制［M］.北京：機械工業出版社，2007：35－36.

［2］Lu Shanping，Fujii Hidetoshi，Nogi Kiyoshi.Effects of CO2Shielding Gas Additions and Welding Speed on GTA Weld Shape［J］.Journal of Materials Science，2005，40（9／10）：2481－2485.

［3］殷樹言.CO2焊接設備原理與調試［M］.北京：機械工業出版社，2000.

［4］李春天，羅怡，杜長華，等.基于凈干伸長的CO2焊接過程動態模型與參數控制［J］.中國機械工程，2009，20（11）：1261－1264.

［5］Magazinnik L T，Magazinnik G G，Magazinnik A G.Power Coefficient and Power Circuits of Modern Inverter－type Elders［J］.Russian Electrical Engineering，2009，80（6）：331－336.

［6］Mironov Y M.Effect of the Secondary Current Lead Resistances on the Properties of an Arc Steelmelting Furnace as a Receiver and Transformer of Electric Power［J］.Russian Metallurgy（Metally），2009（8）：736－740.

［7］許先果，葉延洪，周開慶，等.弧焊過程智能檢測分析系統的建立與應用［J］.中國機械工程，2004，15（15）：1362－1364.

［8］Ramírez M，Trapaga G.Mathematical Modeling of a Direct Current Electric Arc：Part I.Analysis of the Characteristics of a Direct Current Arc［J］.Metallurgical and Materials Transactions B，2004，35（2）：363－372.

［9］Lebedev V A，Romanyuk V S.Single－phase Welding Current Power Sources for Mechanised Carbon Dioxide Welding［J］.Welding International，2004，18（6）：489－493.

［10］Kornilov G P，Nikolaev A A，Yu A，et al.Means and Trends of Reactive Power Management at Large Ironworks［J］.Russian Electrical Engineering，2008，79（5）：248－253.