TCSC次同步諧振阻尼控制器設(shè)計

王 敏，康積濤，李 康，盧紹強

(西南交通大學(xué)電氣工程學(xué)院，四川成都 610031)

輸電線路中引入串聯(lián)電容補償，在增加輸電經(jīng)濟效益的同時會引起電力系統(tǒng)的穩(wěn)定運行問題。當(dāng)采用了串補的輸電系統(tǒng)中的汽輪發(fā)電機組受到擾動時，就會因網(wǎng)機耦合而彼此互激，發(fā)生次同步諧振(subsynchronous resonance，SSR)，導(dǎo)致發(fā)電機軸系扭振，嚴重時造成發(fā)電機軸系損壞，破壞電力系統(tǒng)的安全穩(wěn)定運行。

國內(nèi)外對次同步諧振的抑制措施進行了廣泛而深入的研究，TCSC、SVC等FACTS裝置在次同步諧振的抑制研究上也受到了充分的重視。在研究使用TCSC抑制次同步諧振方面，國內(nèi)外學(xué)者已經(jīng)進行了大量的研究［1－3］。文獻［4］的計算表明，TCSC 在一定的導(dǎo)通角下，具有正電阻特性，從而可以緩解次同步諧振;文獻［5］提出了TCSC主動阻尼控制，通過對TCSC的觸發(fā)調(diào)制，提升系統(tǒng)電氣阻尼來抑制危險模式的振蕩。文獻［6］基于TCSC設(shè)計了一寬帶通單通道SSDC，實現(xiàn)了將整個次同步頻率范圍的電氣阻尼提升為正。

基于提升系統(tǒng)電氣阻尼的思想，在TCSC開環(huán)控制上附加次同步阻尼控制器。該控制器針對分模態(tài)控制方式的不足進行了改進。基于IEEE SSR第一標(biāo)準測試模型［7］在 PSCAD/EMTDC 中使用測試信號法［8］，分析了該控制器對系統(tǒng)電氣阻尼的影響。結(jié)果表明，加入該SSDC能將系統(tǒng)在幾乎整個次同步頻段內(nèi)的電氣阻尼提高為正，即消除了該頻段內(nèi)的SSR危險。

1 TCSC抑制SSR的基本原理

1.1 TCSC 運行原理

TCSC的基本結(jié)構(gòu)如圖1所示，由一個電容器和一個晶閘管控制電抗器(TCR)組成。

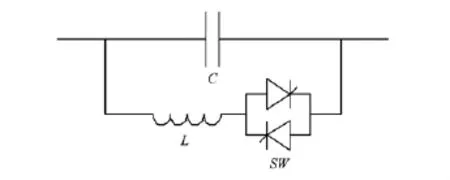
圖1 TCSC基本模塊

穩(wěn)態(tài)運行時，TCSC的等效基波電抗XTCSC與觸發(fā)角α的關(guān)系為

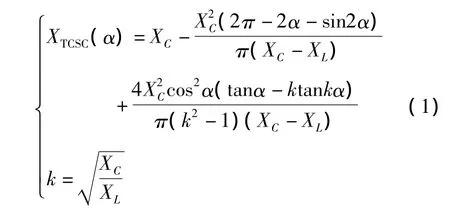
式中，XC為電容器C的基波電抗;XL為α=90°時TCR的等效基波電抗;k為TCSC主回路特征參數(shù)，一般k2=3.3～10，以使觸發(fā)角α變化時，TCSC只出現(xiàn)一個諧振點。

將TCSC電抗XTCSC以XC為基值進行標(biāo)幺化，記Xnet=XTCSC/XC。

1.2 TCSC抑制SSR

由復(fù)轉(zhuǎn)矩系數(shù)法可知，在軸系的某一自然扭振頻率附近，若機械子系統(tǒng)所具有的正阻尼不足以抵消電氣子系統(tǒng)所產(chǎn)生的負阻尼，導(dǎo)致系統(tǒng)對該諧振頻率的總阻尼系數(shù)小于0，則系統(tǒng)將會產(chǎn)生不穩(wěn)定的次同步諧振［9］。這里考慮將機械阻尼設(shè)為0，即考慮機械阻尼最差的情況，這樣在軸系的扭振頻率附近，電氣阻尼為正即可保證系統(tǒng)SSR是穩(wěn)定的。

電氣阻尼定義為［8］

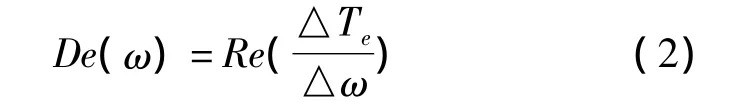
式中，ΔTe為發(fā)電機電磁轉(zhuǎn)矩增量;Δω為發(fā)電機轉(zhuǎn)速偏差。可見，要使電氣系統(tǒng)的阻尼為正，ΔTe與Δω的相位差必須在－90°～90°之間。

發(fā)電機轉(zhuǎn)速偏差Δω包含了各個振蕩模式分量，因此常選作次同步阻尼控制器的輸入信號。SSDC提升阻尼的原理如圖2所示，其中Δω為發(fā)電機轉(zhuǎn)速偏差;Δα為TCSC觸發(fā)角增量;ΔTeDC為產(chǎn)生的發(fā)電機電磁轉(zhuǎn)矩增量;C(s)為SSDC的傳遞函數(shù)，G(s)為TCSC觸發(fā)角增量到ΔTeDC的傳遞函數(shù)。

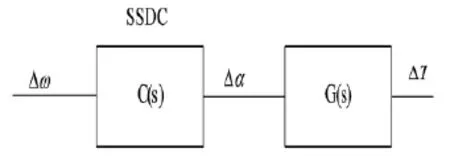
圖2 加入SSDC提升阻尼的原理

添加SSDC后增加的電氣阻尼為［10］

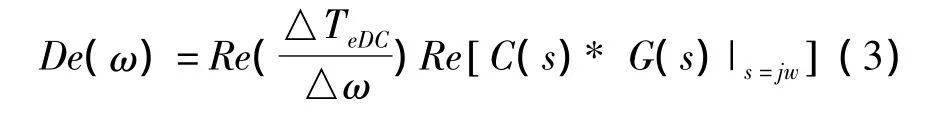
設(shè)計SSDC基本目標(biāo)就是通過恰當(dāng)選擇C(s)的參數(shù)，使得模態(tài)頻率附近，ΔTeDC與 Δω 的 相 位 差 在－90°～90°之間，最終實現(xiàn)將系統(tǒng)電氣阻尼提升為正。

2 系統(tǒng)模型

測試模型是基于IEEE第一標(biāo)準測試系統(tǒng)，并將原系統(tǒng)中部分固定電容用可控串補代替，線路的總串補度為60%，TCSC電抗為線路總電抗的20%，安裝在線路末端，如圖3所示。TCSC的主回路特征參數(shù)k取2.5，穩(wěn)態(tài)觸發(fā)角為157.6°。發(fā)電機軸系采用六軸段模型，即包含5個扭振模式，分別為15.71 Hz、20.21 Hz、25.55 Hz、32.28 Hz、47.45 Hz。系統(tǒng)其他參數(shù)同文獻［7］。

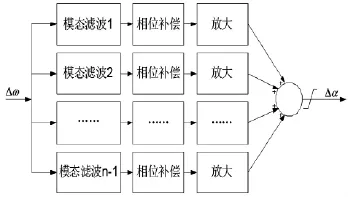
圖3 測試系統(tǒng)模型

3 SSDC設(shè)計

圖3中測試系統(tǒng)具有5個扭振模式，其中模式5由于其模態(tài)阻尼非常大，一般不會發(fā)生網(wǎng)機扭振相互作用，在控制器設(shè)計時不考慮對模式5的影響，只針對前4個模式。

方案1:采用分模態(tài)控制。

采用分模態(tài)控制方式的SSDC如圖4所示，圖中n表示軸段數(shù)，記此控制器為SSDC1。針對可能發(fā)生扭振的4個模式，分別進行濾波、相位補償及放大處理，最終疊加、限幅成為控制器的輸出，即TCSC觸發(fā)角的變化。這種控制器最大的優(yōu)點是針對性強，各分量間的影響小［11］，缺點是可能削弱其他頻率處的電氣阻尼，引起電網(wǎng)中其他發(fā)電機的軸系扭振。

方案2:改進模態(tài)控制。

分模態(tài)控制僅能改善系統(tǒng)在模態(tài)頻率附近的電氣阻尼。針對SSDC1存在的不足，對其進行改進。設(shè)計的控制器結(jié)構(gòu)如圖5所示，記此控制器為SS-DC2。其結(jié)構(gòu)與SSDC1相同，差別在于濾波環(huán)節(jié)通帶較寬。圖中的k，即為控制器的支路數(shù)，與軸段數(shù)n沒有必然的關(guān)系。根據(jù)系統(tǒng)的特點將次同步頻率范圍劃分為數(shù)段，分段補償相位，提升段內(nèi)頻率處的電氣阻尼。各支路阻尼提升效果疊加最終實現(xiàn)將次同步頻率的電氣阻尼提升為正。

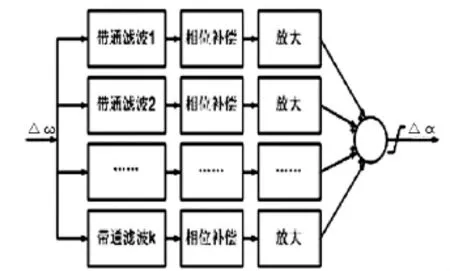
圖4 分模態(tài)控制SSDC的結(jié)構(gòu)

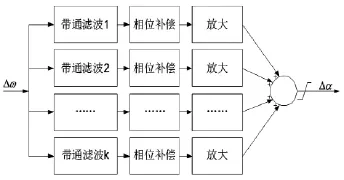
圖5 改進模態(tài)控制SSDC的結(jié)構(gòu)

各支路中相位補償環(huán)節(jié)，補償G(s)及帶通濾波引起的相位差。G(s)的相位可通過測試信號法得到［6，10］，圖6 給出了 Xnet=1.2、1.25、1.3(觸發(fā)角分別為158.8°，157.6°和 156.6°)時的 G(s)相位曲線，其中發(fā)電機運行狀態(tài)為滿載，功率因數(shù)等于0.9(滯后)。

相位補償環(huán)節(jié)采用形如(1+saT)/(1+sT)的超前(滯后)環(huán)節(jié)，當(dāng)a大于1時為超前環(huán)節(jié)，小于1為滯后環(huán)節(jié)，其計算公式如下。

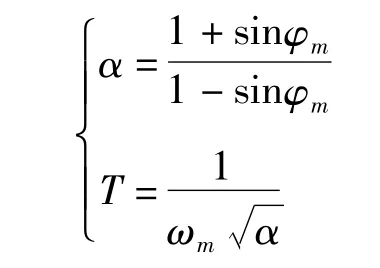
式中，ωm為補償點角頻率;φm為補償點的相角，即最大超前(滯后)角。

SSDC1由于需要相位補償?shù)念l率范圍很窄，其相位補償選擇相對簡單。將各自的補償點分別設(shè)為各模態(tài)頻率點，并選擇合適的補償角度即可。SSDC1參數(shù)見表1。模式4附近頻率由于相位滯后很小，故不設(shè)置相補環(huán)節(jié)。各個模式的濾波及相補環(huán)節(jié)如表1。

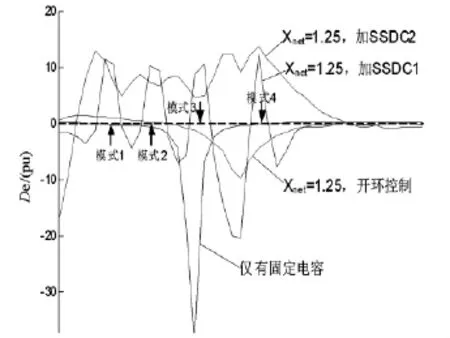
圖6 G(s)的相位特性

表1 SSDC1參數(shù)

針對本系統(tǒng)中發(fā)電機軸系的特點，設(shè)計SSDC2時將次同步頻率分為4段，即SSDC2包含4個支路。各支路分別提升段內(nèi)頻率的電氣阻尼。SSDC2的前3個支路由于G(s)在模式3之前頻率范圍內(nèi)變化緩慢，其設(shè)計思路與SSDC1相同，不再贅述。第4支路在15 Hz處用4個滯后環(huán)節(jié)補償－200°，并用3個超前環(huán)節(jié)在90 Hz處補償135°，以改善該通帶頻率段內(nèi)的負阻尼，使從模式1到模式4的整個頻率段內(nèi)的電氣阻尼都大于0。各個支路的濾波、相補及放大環(huán)節(jié)參數(shù)如表2。

表2 SSDC2參數(shù)

4 仿真分析

4.1 電氣阻尼分析

選擇TCSC 的穩(wěn)態(tài)觸發(fā)角為157.6°，即Xnet=1.25。發(fā)電機運行狀態(tài)為滿載，功率因數(shù)等于0.9(滯后)。為驗證所設(shè)計的SSDC抑制SSR的有效性，考慮以下4種運行工況。

工況1:TCSC不投入，即TCSC等效為固定電容。

工況2:TCSC投入，采用開環(huán)控制。

工況3:TCSC投入，在開環(huán)控制上附加SSDC1。

工況4:TCSC投入，在開環(huán)控制上附加SSDC2。

采用測試信號法分析了4種工況下的電氣阻尼，如圖7所示。可以看到，全部采用固定電容補償時，系統(tǒng)在4個模式附近的電氣阻尼都為負，系統(tǒng)SSR不穩(wěn)定。工況2下，TCSC的投入引起系統(tǒng)諧振頻率的右移，模式1、2附近的電氣阻尼有所增大，但在模式3、4附近的阻尼為負，系統(tǒng)仍為 SSR不穩(wěn)定。工況3，加裝所設(shè)計的SSDC1后，各個模式頻率處的電氣阻尼均為正。而工況4，加裝所設(shè)計的SSDC2后，從13 Hz到40 Hz內(nèi)的電氣阻尼均為正，相對采用分模態(tài)控制思想設(shè)計的SSDC1，阻尼為正的范圍不再局限在模式頻率附近，亦即消除了這一整個頻率段內(nèi)的SSR危險。

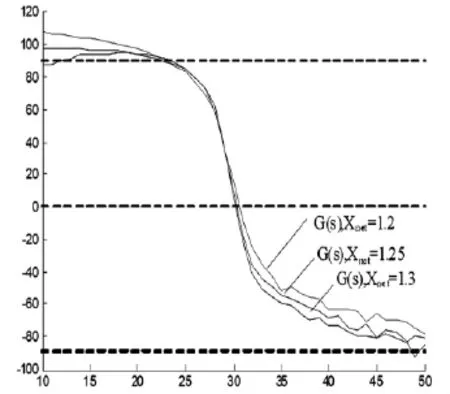
圖7 4種工況下的電氣阻尼曲線

4.2 暫態(tài)時域仿真

為進一步驗證SSDC2抑制SSR的有效性，利用PSCAD/EMTDC對圖3所示系統(tǒng)進行時域仿真。發(fā)電機軸系采用六軸段模型，機械阻尼設(shè)為0。待系統(tǒng)進入穩(wěn)態(tài)后，t=2.5 s時刻，圖3中母線B發(fā)生三相接地短路故障，故障持續(xù)0.05 s后切除。圖8給出了系統(tǒng)在工況4下的各軸段間的扭矩，可以看出在使用了所設(shè)計的SSDC2之后，各軸段間的扭矩逐漸衰減并最終回到原穩(wěn)態(tài)，系統(tǒng)SSR穩(wěn)定。

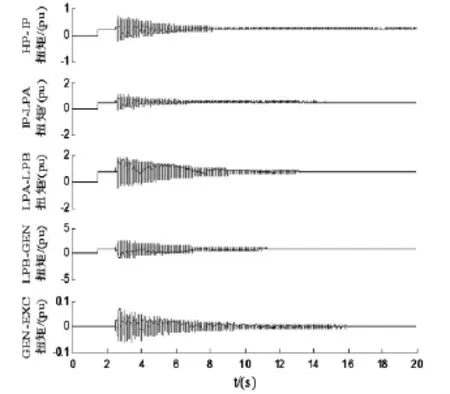
圖8 工況4加SSDC2后發(fā)電機軸段扭矩

5 結(jié)論

基于提升系統(tǒng)電氣阻尼的思想，設(shè)計了TCSC次同步阻尼控制器。該控制器針對分模態(tài)控制方式的不足進行了改進。結(jié)果表明，加入該控制器能將系統(tǒng)在幾乎整個次同步頻段內(nèi)的電氣阻尼提高為正，即消除了該頻段內(nèi)的SSR危險，因而具有很強的工程實用性和通用性。

［1］S.S.Choi，F(xiàn).Jiang，G.Shrestha.Suppression of Transmission System Oscillations by Thyristor－controlled Series Compensation［J］.IEE Proc.－ Gener.Transm.Distrib.1996，143(1):7 －12.

［2］Brian K.Perkins，M.R.Iravani.Dynamic Modeling of a TCSC with Application to SSR Analysis［J］.IEEE Transactions on Power Systems，1997，12(4):1619 －1625.

［3］葛俊，童陸園，耿俊成，等.TCSC抑制次同步諧振的機理研究及其參數(shù)設(shè)計［J］.中國電機工程學(xué)報，2002，22(6):25－29.

［4］呂世榮，劉曉鵬，郭強，等.TCSC對抑制次同步諧振的機理分析［J］.電力系統(tǒng)自動化，1999，23(6):14－18.

［5］周長春，劉前進，Lennart A..ngquist，等.抑制次同步諧振的TCSC主動阻尼控制［J］.中國電機工程學(xué)報，2008，28(10):130 －135.

［6］鄭翔，徐政，張靜.TCSC次同步諧振附加阻尼控制器［J］.電工技術(shù)學(xué)報，2011，26(2):181 －186.

［7］IEEE Subsynchronous Resonance Working Group.First Benchmark Model for Computer Simulation of Subsynchronous Resonance［J］.IEEE Transactions on Power ApparatusandSystems，1977，96(5):1565 －1572.

［8］徐政.復(fù)轉(zhuǎn)矩系數(shù)法的適用性分析及其時域仿真實現(xiàn)［J］.中國電機工程學(xué)報，2000，20(6):1－4.

［9］程時杰，曹一家，江全元.電力系統(tǒng)次同步振蕩的理論與方法［M］.北京:科學(xué)出版社，2009.

［10］張靜，徐政，鄭翔，等.SVC抑制SSR的機理及控制器設(shè)計［J］.南方電網(wǎng)技術(shù)，2010，4(3):57－61.

［11］張丹.高壓直流輸電系統(tǒng)次同步振蕩的特征值分析與控制［D］.北京:華北電力大學(xué)，2011.