含圓孔有限厚度板的三維彈塑性分析

□胡天翼 □劉 寧 □邱明星（西安交通大學）

1.前言

含圓孔平板在自身受力時出現的應力集中問題是工程中普遍存在的問題，其平面模型是彈性力學中的經典模型，已有了精確的解析。與平面問題相比，考慮了厚度效應和三維尺寸效應的三維分析更加符合工程實際，因此也更具有指導意義；同時伴隨受力增加材料進入彈塑性狀態時，也會出現許多彈性狀態下不具有的特性。然而由于三維狀態下的帶孔板不僅在圓孔周圍存在應力集中，同時還存在復雜的三維效應區，應力結構十分復雜，應力集中與平面狀態有著本質不同；加之構件塑性區的不斷增大還會導致圓孔周圍應力集中的重新分布，亦與彈性狀態有著顯著差別，討論起來十分繁瑣。因此目前對帶圓孔板的研究主要集中于對構件進行彈性分析；或假定平板厚度足夠小，使各項參數能夠在厚度方向均勻分布。朱曉東等對不同尺寸含圓孔板的應力集中情況作了橫向對比，但其結果只適用于處在彈性階段的材料。

文章通過對含圓孔平板的三維有限元計算，研究了構件處于彈塑性階段時三維應力場的分布，分析了彈塑性狀態下應力集中的大小和位置與材料尺寸、受力之間的關系，同時還描述了彈塑性狀態下圓孔附近三維應力的約束程度。文章主要選取試樣厚度作為變量，來對比三維試樣與二維試樣、彈塑性分析與彈性分析之間的異同。

2.分析參數的定義和有限元模型介紹

2.1 分析參數的定義

在物體幾何形狀或載荷發生突變的地方，會出現隨著遠離突變點而迅速衰減的局部高應力，這種現象稱為應力集中。通常用應力集中系數

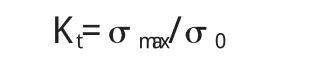
來表示其嚴重程度，式中σmax為最大局部應力，為不考慮局部效應時的計算應力，稱為名義應力。由于局部高應力是引起疲勞裂紋或脆性斷裂的根源，所以確切的應力集中數據對構件和機械設計至關重要。

為了更清楚地描述有限厚度板圓孔邊緣附近應力場的三維特性以及離面應力的影響，引入一個約束參數來描述沿厚度的應力分布情況，即離面約束系數

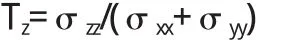
式中：σxx、σyy、σzz分別為 x、y、z方向的正應力。在彈性階段Tz介于0和之間，Tz=0和Tz=ν分別對應于平面應力和平面應變狀態，ν為材料的泊松比。

2.2 有限元分析模型

由前所述，三維彈塑性狀態應力結構十分復雜，因此模型計算借助大型有限元計算軟件ANSYS-10.0完成。選取1/8試樣，坐標原點位于板厚中面圓心，在試樣長度、寬度、厚度中面加載對稱約束，圓孔遠端沿y方向加載大小為N的均勻拉應力。圓孔的半徑r=10mm，板的長度 2L=400mm，寬度 2W=200mm(當 r/W<5時，可近似認為圓孔很小，試樣為無限大)，厚度為2B，如圖1所示：

圖1 模型的網格劃分圖

在分析中，采用8節點三維實體單元，沿試樣的1/2厚度處取15層單元，每層單元的厚度從板的厚度中面到表面逐漸減小，間距比率取0.1。在每一單元層的圓孔周圍畫出三倍半徑大小的細化區，采用映射劃分(應力集中和塑性區主要出現在三倍半徑范圍以內)，三倍半徑以外區域單元尺寸較大(經實測將二維平板照此方式劃分網格，計算結果能很好地符合解析解，誤差在1%以內)。在板遠端作用有σ的均勻分布拉應力，材料的彈性模量和泊松比分別為200G和0.3，屈服強度300MPa，切線模量為0，本構關系見圖2。

圖2 材料本構的定義圖

3.計算結果分析

3.1 試樣塑性區的擴展

塑性區是指試件內部出現塑性應變的部分，在彈塑性分析中，塑性區的位置和大小對試樣性能有著直接的影響，同時塑性區的存在也是材料會表現出異于彈性狀態的性能的關鍵。因此，對試樣隨著受力增加導致的塑性區范圍的擴大有一個直觀的認識非常有必要。

試樣取固定尺寸 2L=400，2W=200，B=15，r=10。由于材料屈服強度設定為300MPa，因此在加載拉力N達到接近100MPa的值時材料會保持彈性狀態。這里將N分別取120MPa、150 MPa、170MPa、200MPa、230MPa和 260MPa，作出在上述拉力下圓孔邊緣左視圖屈服區的分布。

圖1中左面為試樣中面，左下角落為中面圓孔根部，由下向上為y軸正方向，由左向右為z軸正方向，圖中彩色部分都為塑性應變區。從圖中可以看出，三維帶圓孔板的應力集中最大處往往出現在y=0的試樣受拉對稱面上。隨著拉力的增大，屈服區自試樣中面圓孔根部開始向外擴展，屈服區的應變值亦隨拉力的增大而增大，尤其是拉力為230MPa和260MPa時，塑性區已經達到很大。

3.2 圓孔根部三維應力場分析

為清楚描述處于彈塑性狀態的三維試樣應力分布，我們自Ansys中提取模型受力對稱面(即y=0面)，分別對x、y、z三向應力做出三維分布圖。統一取八分之一模型，B=15mm，L=200mm，W=100mm，r=10mm，N=230MPa(230MPa已經接近平面應力狀態的材料能承受的最大值)。

3.2.1 當σx沿x和厚度z的分布,z=0為板的厚度中面，x/r=0為圓孔邊緣。在x方向上，σx初始值為0，從離開圓孔表面后急劇上升，在距圓孔邊緣約一倍半徑處達到最大值，隨后開始逐漸下降，在距圓孔邊緣約五倍半徑以后幾乎趨近于零；在z方向上，σx在厚度中面值最大，然后隨距中面距離的增大緩慢減小，減小的幅度逐漸增大，在接近表面處約z=12時達到最小值，然后隨著距表面距離的減小而略有回升。

3.2.2 當σy沿x和厚度z的分布，在x方向上，當x/r=0即在圓孔邊緣時，σy的值己經很大，然后隨距圓孔邊緣距離的增大而急劇上升，在約一倍半徑內達到最大值，后又急速單調下降，在3倍半徑距離遠處已逐漸趨于N=230MPa；在z方向上，可以看到在板的厚度中面(z=0)σy的值最大，隨著離中面距離的增大σy逐漸下降且下降幅度遞增。

與彈性狀態相比，處于彈性狀態的材料σy的最大值應在圓孔根部即x/r=0處取得。但對處于彈塑性狀態的試樣，σy的最大值處總是距離圓孔根部在x方向有一定距離，此處也是應力集中最為明顯的位置，對于整個試樣的應力集中系數最大值Ktmax也應在此處取得[3]。

3.2.3 當σz沿x和厚度z的分布，在x方向上，可以看出σz所產生影響的區域大約在距圓孔表面的一倍半徑的范圍內，變化規律為先隨離圓孔邊緣距離的增加增大達最大值后急劇下降，在一倍半徑范圍以外σz的值基本為零；在z方向上，σz在板厚中面的值最大，后隨著離中面距離的增大而逐漸減小，離表面越近減小的速度越快，在達到表面時己降到零。

與彈性狀態所不同的是，處于彈性狀態的式樣σz沿x方向的分布是單調遞減的，并不存在在圓孔附近的上升段，其離面約束系數Tz也總在x=0處取得；相比之下彈塑性狀態的試樣在圓孔附近一倍半徑的范圍內，才能達到最大值。另外由上述分析可知，無論是σx、σy還是σz，其沿厚度方向都不是均勻分布的。略作對比便可知，三維狀態下某一位置厚度方向的應力最大值總是大于相同條件下平面狀態的應力值，因此在實際工程中考慮材料的三維效應很有必要。

3.3 三維彈塑性狀態應力集中的分析

應力集中系數是衡量圓孔邊緣應力集中程度的重要參數，本段內容分別取B為變量，討論不同情況下三維彈塑性試樣的應力集中系數變化。

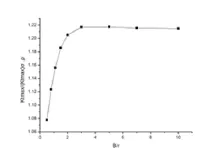
圖3 不同板厚B時最大應力集中系數的分布規律圖

圖3為 r=10，L=200mm，W=100mm，N=230MPa的情況下，不同厚度下試樣內部應力集中最大值的點的應力集中系數Ktmax的橫向比較，同樣采取了和相同條件下平面狀態的應力集中系數最大值(Ktmax)σ,ρ比值的方式表現。從圖中可以看出，三維狀態的試樣Ktmax不僅恒>二維狀態，且隨厚度增加試樣的應力集中程度也急劇增加，后在板厚為2倍圓孔半徑處開始放緩，最終在板厚達到3倍孔徑后到達最大值1.21，其后基本保持不變。也即是說，當板厚達到3倍圓孔直徑以上時，可認為彈塑性試樣的應力集中最為嚴重。

圖4為 r=10，L=200mm，W=100mm，N=230MPa的情況下，不同厚度下圓孔根部(x=r，y=0處)應力集中系數Kt沿厚度z的分布，為了和平面狀態作對比，圖中Kt皆以與相同條件下二維平面應力狀態的應力集中系數(Kt)σ,ρ比值的形式表現。可以看到，三維狀態圓孔根部的應力集中系數是恒大于二維狀態的。應力集中系數總體是隨板厚增加而增加的，對特定厚度而言應力集中系數Kt的最大值總是在中面處，與彈性狀態相比之下并未出現板過厚時應力集中最大值位置逐漸向板表面移動的現象[3]。當板厚達到圓孔半徑的約三倍以后Kt便保持在平面狀態的1.18倍附近不再增加。Kt從厚度中面到表面總體呈遞減趨勢，且隨著距離板表面越近減小的越急劇，但在板厚達到圓孔半徑的三倍以后，隨板厚的增加Kt能在越來越大的厚度范圍內保持其最大值，即應力集中控制了大部分的厚度，而后急速下降并最終趨近于1。

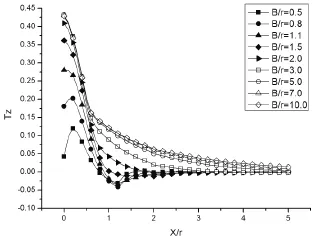
圖4 不同板厚B時圓孔根部應力集中系數沿厚度z的分布圖

3.4 三維彈塑性狀態離面約束的分析

為揭示三維狀態下試樣離面應力的分布，有必要對離面約束Tz進行深入分析。本段內容依舊分別取B為變量，討論不同情況下三維彈塑性試樣的離面約束系數變化。

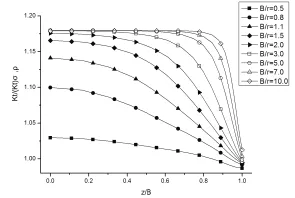
圖5 不同板厚下試樣中面離面約束系數沿x的分布圖

圖5為 r=10mm，L=200mm，W=100mm，N=230MPa的情況下，不同板厚下的離面約束系數Tz沿x的分布，可以看到，不同的板厚下，離面約束Tz沿x的分布有些微差別，在板厚較大時，離面約束Tz的最大值幾乎出現在圓孔邊緣，然后隨著到圓孔邊緣距離的增大而單調遞減，遞減速度隨x的增大而減小，最后逐漸趨近于0；與彈性狀態不同的是，在板厚較小時,離面約束Tz的最大值位置己經逐漸偏離圓孔邊緣，在圓孔附近區域Tz呈先增大到最大值后減小，后急速減小至最小值(負值)，后又上升趨于零。可以觀察到，板厚越大離面約束Tz的最大值越大，且最大值的位置離圓孔邊緣越近，隨著板厚的增大，Tz最大值增大的幅度減小，Tz的影響區域大約在距圓孔邊緣3倍半徑內。

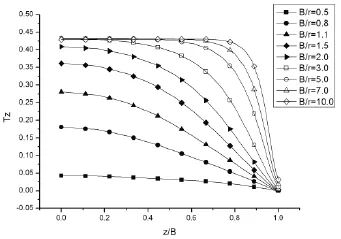
圖6 不同板厚的圓孔根部離面約束系數沿厚度z的分布圖

圖6為 r=10，L=200mm，W=100mm，N=230MPa的情況下，不同厚度下的離面約束系數Tz沿厚度z的分布。可以看到，離面約束系數總體是隨板厚增加而增加的，但不論厚度大小，對特定厚度而言離面約束Tz的最大值總是在中面處，該最大值起初隨著板厚的增加而增加，然而當板厚達到圓孔半徑的約三倍以后便保持在0.43附近不再增加，Tz從厚度中面到表面總體呈遞減趨勢，且隨著距離板表面越近減小的越急劇，但在板厚達到圓孔半徑的三倍以后，隨板厚的增加Tz能在越來越大的厚度范圍內保持其最大值，而后急速下降并在表面處降至零。該結果與彈性狀態的結果類似[3]，但由于圓孔周圍彈塑性的應力限制，使得試樣的離面應力系數總是遠遠>彈性狀態的分析結果 (N=230時圓孔根部整個厚度方向已經全部進入塑性狀態，Tz普遍比彈性狀態大一倍)。

4.結論

一是處于彈塑性狀態的三維試樣，其應力分布與彈性狀態有著明顯不同。由于受到塑性區的影響，σy和σz的最大值都不一定在圓孔根部(x=0)處取得，這進一步導致了應力集中系數和離面約束系數沿x分布的特殊性。在x方向上，應力集中系數出現了先升后降的情況，并受塑性區影響在曲線路徑上出現了折點；離面約束系數也在一定厚度出現了同樣現象，并且最小值降低到了負值，這些都是彈性狀態的分析中未曾出現的新情況。

二是三維狀態下材料的應力集中程度普遍大于平面應力狀態，彈塑性狀態下材料的離面約束也普遍大于彈性狀態，因此將三維問題按照平面問題來考慮或是將彈塑性問題按照彈性問題來分析都是偏不安全的。在三維彈塑性情況下，材料的離面約束影響力約在3倍半徑以內，應力集中亦在試樣厚度達到圓孔直徑的3倍以上時達到最大。

三是三維彈塑性材料模型的應力-應變分布是一個受多種因素耦合作用的結果，其中外加荷載、尺寸效應(如三維板厚、孔徑大小)都會對分析結果產生由量到質的影響。另外，材料塑性程度越高最大應力集中系數Ktmax相對越低，但與彈性狀態相比，Ktmax所在位置出現了偏離圓孔根部的情況。