導彈協同制導中末交接班目標截獲概率研究

付昭旺，于 雷，寇英信，徐 安

（空軍工程大學 工程學院，西安710038）

多機協同空戰已成為現代空戰的主要作戰模式，導彈協同攻擊是協同作戰的核心，而協同制導是導彈協同攻擊的關鍵環節，直接影響協同作戰效果.近年來，國內對導彈協同制導問題展開了研究，內容涉及協同制導的原理和關鍵技術[1，2]、協同制導決策方法[3，4]、導彈協同制導的導引律[5]等.協同制導條件下，發射載機和制導載機相分離，制導交接誤差、目標參數測量誤差、載機定位誤差和導彈傳遞對準誤差等誤差源會降低修正指令的精度，直接影響導彈中制導的效果.目前對于導彈協同制導的制導能力和制導效果缺乏研究.文獻[6]對協同制導條件下的中、末交接班能力進行了一些研究，但是考慮的誤差因素簡單，未建立誤差傳遞模型，無法對誤差影響下的制導精度進行定量評估.基于此，本文通過對協同制導的信息流和誤差源傳遞進行分析，并建立誤差源與目標截獲概率的定量模型，為導彈協同制導效果評估提供理論依據.

1 導彈協同制導數學建模

以典型的雙機協同制導為例進行建模研究，將發射導彈的載機稱為交班載機（Quit Fighter，QF），將參與接替制導的載機稱為接班載機（Succeeded Fighter，SF）.制導交接后，QF退出，由SF接替制導，以周期T向導彈發送指令，修正其飛行方向和姿態，在滿足中末制導交接條件時，導引頭開機搜索，截獲目標后轉入末制導.

1.1 制導慣性坐標系的建立

為實現協同制導，必須建立一個統一的制導慣性坐標系，制導慣性坐標系由QF建立并完成與導彈的傳遞對準，并通過制導交接傳遞給SF.本文建立如下制導慣性坐標系：導彈發射前與QF傳遞對準完成時刻，以QF所在位置的“北、天、東”地理坐標系作為制導慣性坐標系.

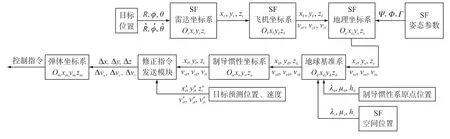
圖1 協同制導修正指令計算流程

1.2 協同制導修正指令的計算流程

協同制導修正指令的計算需要經過多次坐標轉換.本文建立如圖1所示的修正指令計算流程.文中相關坐標系的定義及轉換關系見文獻[7].QF和SF的地理位置均采用WGS－84地球模型定義的經度、緯度和海拔高度來表示.圖1中，R，φ，θ為SF雷達測得的目標參數，分別為目標距離、方位角及俯仰角；xr，yr，zr為Orxryrzr下的目標位置；xf，yf，zf和vxf，vyf，vzf分別為SF在Ofxfyfzf下的目標位置和速度；Ψ，Φ和Γ分別為SF的機體航向角、俯仰角和滾轉角，xe，ye，ze為Oexeyeze下的目標位置；λ0，μ0，h0（經度、緯度和高度）為Odxdydzd下Ooxoyozo的原點所在的位置；λz，μz，hz為Odxdydzd下SF所在的空間位置；xd，yd，zd為Odxdydzd下的目標位置；xt，yt，zt和vxt，vyt，vzt分別為Ooxoyozo下的目標實際位置和速度；x′t，y′t，z′t和v′xt，v′yt，v′zt分別為目標預測的位置和速度；Δx，Δy，Δz和 Δvx，Δvy，Δvz分別為目標的位置偏差和速度偏差.

1.3 修正指令計算模型

根據修正指令計算流程，以位置修正指令計算為例，給出其矢量法計算方法，速度修正指令的計算與位置修正指令計算類似.

Orxryrzr系下的目標位置為

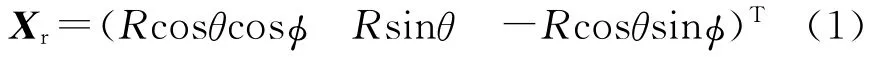
Ofxfyfzf下的目標位置為

式中，Tf，r為Orxryrzr到Ofxfyfzf的轉換矩陣.

Oexeyeze下的目標位置為

式中，Te，f為Ofxfyfzf到Oexeyeze的轉換矩陣.

Odxdydzd下的目標位置為

式中，Xde為Odxdydzd下Oexeyeze原點的位置，Td，e為Oexeyeze到Odxdydzd的轉換矩陣.

Ooxoyozo下目標的位置為

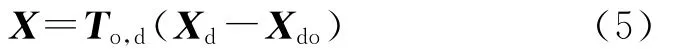
式中，Xdo為Odxdydzd下Ooxoyozo原點的位置，To，d為Odxdydzd到Ooxoyozo的轉換矩陣.

設計算得到t時刻Ooxoyozo下的目標位置X和目標速度vt，設t時刻導彈預測的目標位置為X′、預測速度為v′t，則對目標的位置修正和速度修正指令分別為ΔX＝X－X′和Δv＝vt－v′t.

2 導彈協同制導誤差模型

導彈協同制導包括目標參數測量、指令計算、指令傳輸和彈體運動等過程.指令計算需要引入SF的空間位置和姿態參數，并經過多次坐標轉換，與單機自主制導相比，協同制導誤差源增多，對制導精度產生影響.為研究協同制導的效果，必須對協同制導誤差進行建模分析.

2.1 影響協同制導的主要誤差源

協同制導引入的誤差源主要有以下6項：①SF雷達的測量誤差；②SF的空間定位誤差；③SF姿態測量誤差；④QF與導彈的傳遞對準誤差；⑤修正指令延時誤差；⑥導彈的狀態估計誤差.這6種誤差源相互獨立，作用于導彈中制導的不同環節，其中，①、②、③和④產生和影響修正指令的計算誤差，⑤和⑥影響指令的執行誤差，它們都直接影響導彈中末交接班的交接效果.

2.2 誤差特性分析

雷達測量誤差可以認為是一種服從零均值正態分布的隨機誤差，可采用測距精度δR和測角精度δφ、δθ來描述；載機姿態測量誤差與姿態傳感器的測量精度有關，可采用姿態角誤差δΨ、δΦ和δΓ來描述；載機的空間定位誤差由飛機導航系統產生，由于載機的地理位置采用經度、緯度和高度來表示，SF的空間定位誤差可采用經度誤差δλz、緯度誤差δμz和高度誤差δhz來度量；傳遞對準誤差由導彈慣性坐標系O′ox′oy′oz′o與制導慣性系Ooxoyozo之間存在失準角δω而引入，δω的大小可由載機火控系統和武器系統的性能參數得到；指令延時誤差是由于SF修正指令延時而影響導彈對目標機動的準確估計，可以等同于目標機動估計誤差，指令延時誤差主要由制導交接延時、SF與QF的系統時鐘偏差、指令接收延時和指令處理延時引起；導彈狀態估計誤差由彈載慣導引起，與導彈的工作時間和飛行軌跡有關，具有累積效應，可采用慣導精度δm來描述.

2.3 誤差計算模型

設SF雷達測距誤差為δR，方位測角誤差為δφ，俯仰測角誤差為δθ，則由機載雷達測量引起的目標位置估計誤差為

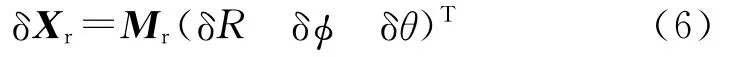
考慮雷達測量誤差，式（1）中的Xr變為

Ofxfyfzf下的目標估計位置為

考慮 QF的姿態誤差，式（3）中的Te，f變為

則Oexeyeze下的目標估計位置為

同理，考慮到SF的空間定位誤差，有：

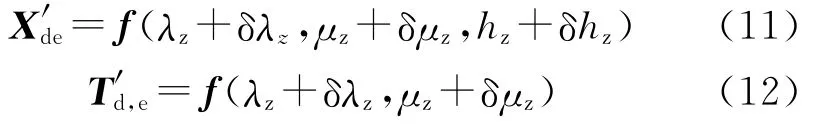
則Odxdydzd下的目標估計位置為

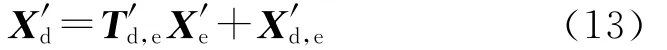
Ooxoyozo下的目標位置為

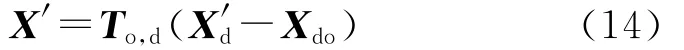
考慮導彈發射的傳遞對準誤差，導彈慣性系O′ox′oy′oz′o下目標的估計位置為

式中，反對稱矩陣Tω＝f（δωx，δωy，δωz）.

在修正指令延時Δt內，導彈以目標作勻速直線運動進行位置估計，但是，導彈發射后，目標必然進行逃逸機動，則指令延時引入誤差為對目標的機動估計誤差，可采用下式進行計算[2]：

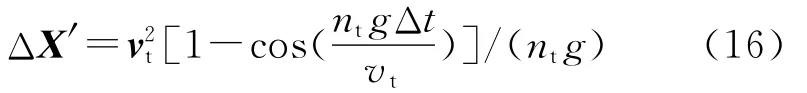
式中，nt為目標過載，vt為目標速度.

在上述誤差源疊加作用下，O′ox′oy′oz′o下的目標位置估計誤差為

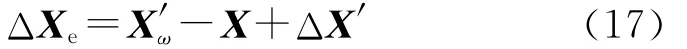
所有誤差源相互獨立，于是O′ox′oy′oz′o下目標位置估計誤差的方差可表示為

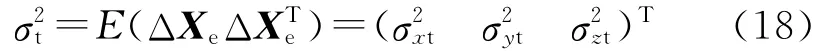
導彈慣性導航系統的定位誤差可表示為

式中，δm為慣導的定位精度，t為導彈飛行時間.

則O′ox′oy′oz′o下導彈位置估計誤差的方差為

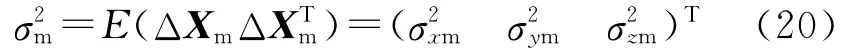
由于 ΔXe和 ΔXm相互獨立，于是O′ox′oy′oz′o下導彈和目標相對位置估計誤差的方差為

Omxmymzm下目標位置估計誤差的方差為

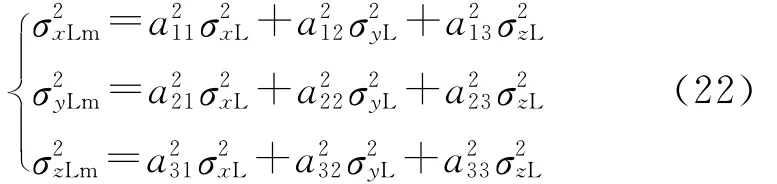
式中，aij（i，j＝1，2，3）為導彈慣性坐標系到彈體坐標系的轉換矩陣中的系數.

3 目標截獲概率計算模型

中末制導交接班的目標截獲包括角度截獲、距離截獲和速度截獲，分別設三者的截獲概率為Pa、Pr和Pv，則目標截獲概率可以表示為

本文主要研究導引頭的角度截獲問題，令Pr＝Pv＝1.角度截獲概率是指目標實際視線落入雷達導引頭視場的概率，取決于導彈的導引頭指向誤差和導引頭視場的寬度.導引頭指向角誤差φa只需考慮垂直于導引頭視線平面的y軸和z軸方向的分量φya和φza.φa的概率分布應取決于二維隨機變量（φya，φza）的概率密度函數[8]：

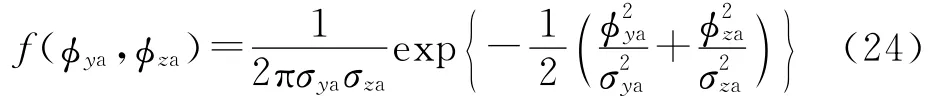
式中，σka＝arctan（σkLm/Ds）（k＝y，z），Ds為導引頭的預定交班距離[2].

由于角度截獲需要方位和俯仰同時滿足截獲條件，令σa＝max（σya，σza），則有：

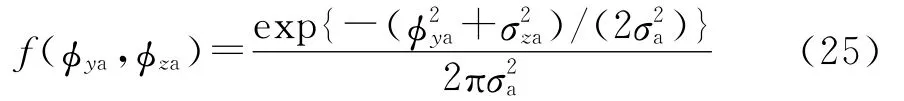
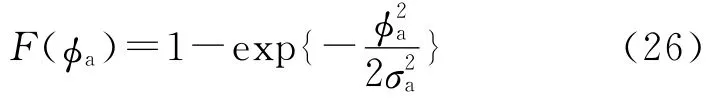
設導引頭半視場的寬度為α，則有：

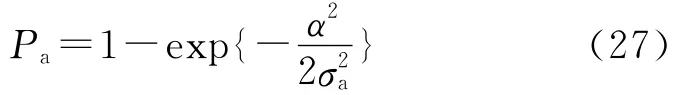
4 協同制導截獲概率仿真研究

根據所建立的模型對協同制導目標截獲概率進行仿真.針對每種誤差源條件仿真N次，對誤差進行統計，再根據統計量計算截獲概率.仿真條件設置如下：λ0＝110.105°，μ0＝60.051°，h0＝6km；導彈初速vm＝450 m/s，α＝2.5°，導引頭的預訂交班距離Ds＝15km.目標初始位置為：xt＝30km，yt＝8km，zt＝0，vt＝1 080km/h，ψt＝－40°.導彈發射后目標以6g的過載作水平蛇形機動.SF的初始位置：λz＝110.366°，μz＝59.722°，hz＝10km，Ψz＝30°，vz＝900km/h.SF 與 目 標 的 初 始 距 離 為68.3km，指令周期為0.5s，取N＝50，P0＝1，仿真誤差條件如表1所示.

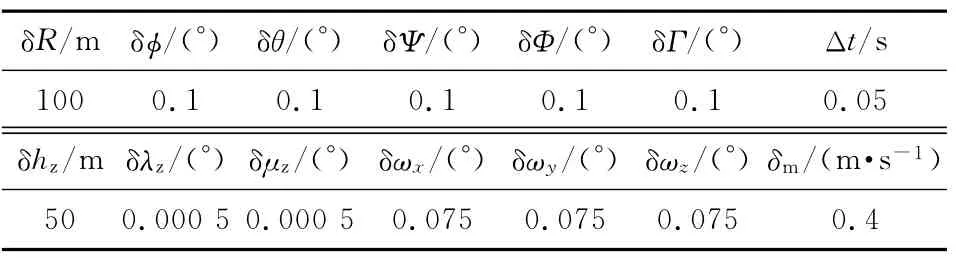
表1 仿真誤差條件

仿真得到中末交班平均時間為31.65s，一次典型的彈道軌跡如圖2所示.目標估計位置與實際位置相比存在動態估計誤差，該誤差將直接影響中末交接班的目標截獲概率.

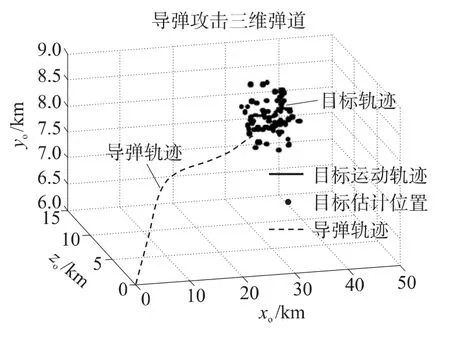
圖2 協同制導仿真彈道軌跡曲線

為定量分析各誤差對Pa的影響，保留初始條件不變，依次逐項改變誤差項進行仿真.仿真結果如圖3～圖7所示.

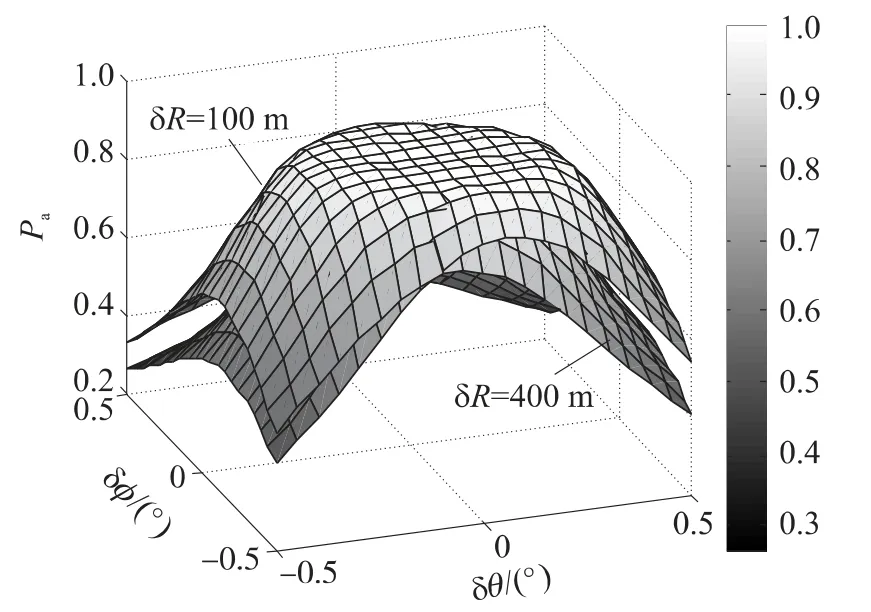
圖3 δR，δφ和δθ與Pa的關系

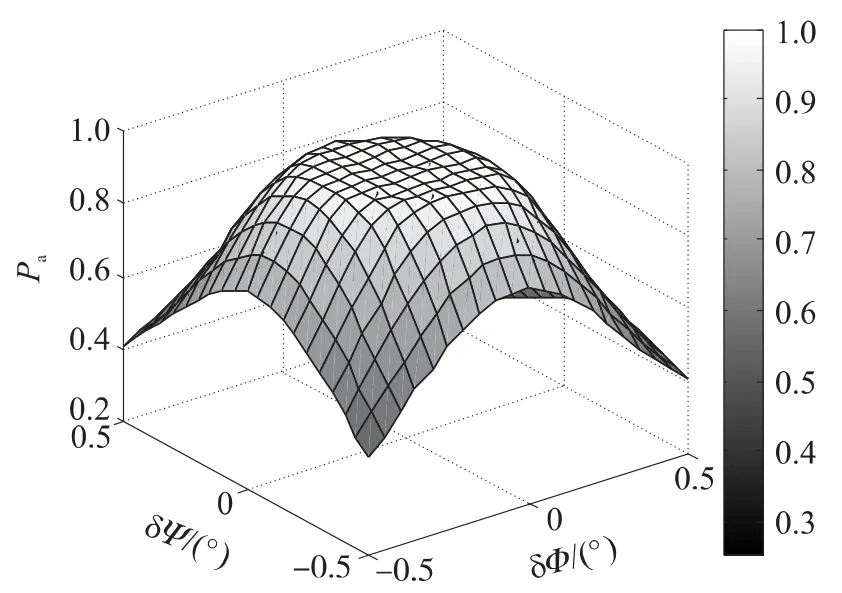
圖4 δΨ和δΦ與Pa的關系

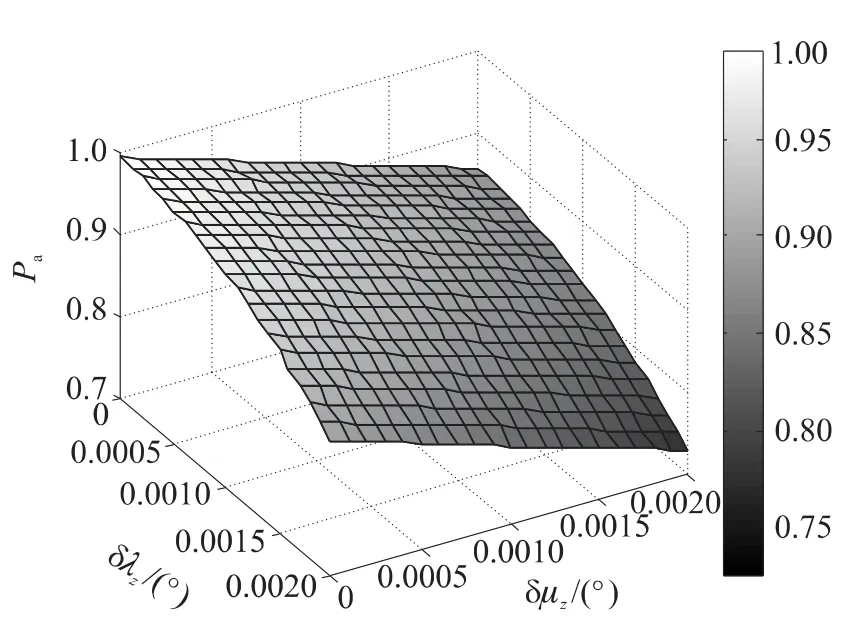
圖5 δλz和δμz與Pa關系

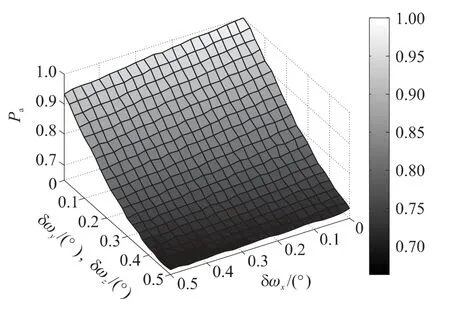
圖6 δω與Pa的關系

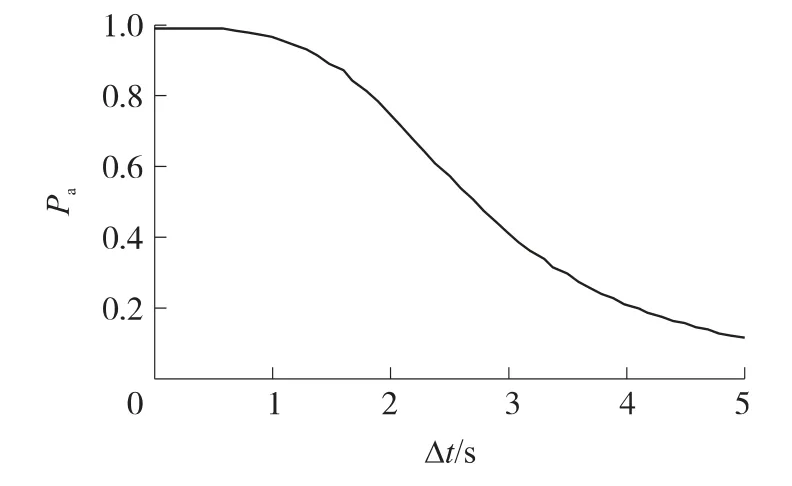
圖7 Δt與Pa的關系曲線

由圖3可以看出，SF雷達測角精度較高時，對Pa影響很小，δφ＜0.2°且δθ＜0.2°時，Pa≥0.98，測角誤差增大時，對Pa影響增大，在δφ＞0.2°且δθ＞0.2°時，Pa隨δφ和δθ的增大而迅速下降，當δφ＞0.5°且δθ＞0.5°時，Pa＜0.5.

由圖4可以看出，SF姿態測量精度較高時，對Pa影響很小，δΨ＜0.15°且δΦ＜0.15°時，Pa＞0.98，測量誤差增大時，對Pa影響較大.

由圖5可以看出，SF空間定位誤差對Pa影響較小，在δλz＝δμz＜0.000 5°時，Pa＞0.96，在δλz＝δμz＜0.001 5°時，Pa＞0.8.

由圖6可以看出，Pa對小幅度的傳遞對準誤差較為敏感，而隨著誤差的增大，敏感度降低，總體來看，影響不明顯.

由圖7可以看出，Δt較小時，對Pa影響很小，Δt＜0.8s時，Pa＞0.98，Δt增大時，Pa隨 Δt增大而迅速下降，Δt＞2.7s時，Pa＜0.5.

顯然，各誤差源對截獲概率的影響程度不同，但是影響趨勢大致類似.為了對比各誤差源對Pa的影響，對Pa進行靈敏度分析，以E表示靈敏度，以ΔSX表示參數X的相對誤差，得到如圖8所示的靈敏度曲線.由圖8可以看出，Pa對Δt的敏感性最高，其次是機載雷達測量誤差，而對空間定位誤差敏感性最低.在相對誤差較小時（小于0.6），Pa對傳遞對準誤差的敏感性較高，反之，對姿態測量誤差敏感性更高.

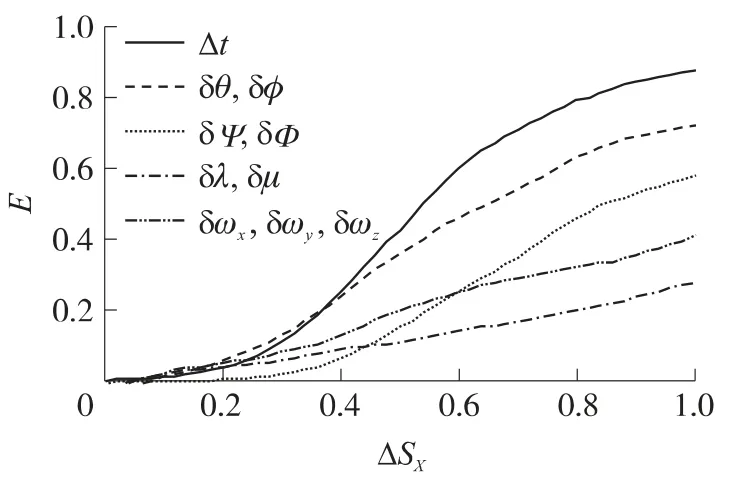
圖8 誤差源的靈敏度曲線

綜上所述，為提高協同制導的目標截獲概率，可采取如下措施：①協同編隊應建立精確的統一時鐘來保證協同制導精確的時間同步；②對協同制導的SF進行決策，盡可能選擇雷達測量精度高或距目標較近的SF進行制導；③為SF裝備高精度慣導系統或采用組合導航技術，提高其姿態測量精度和定位精度；④提升QF與導彈的傳遞對準精度，在導彈完成精對準后再發射.

5 結束語

本文基于協同制導的信息流和誤差傳遞關系對協同制導精度進行建模研究，得到了誤差源與目標截獲概率之間的定量分析模型，并對誤差靈敏度進行了仿真分析.結果表明：修正指令的延時誤差、制導載機的雷達測量精度和姿態精度對目標截獲概率影響較大，建立高精度的協同數據鏈，并選擇雷達性能優良的載機進行協同制導是非常必要的.本文的研究為導彈協同制導作戰效果評估奠定了基礎，并對導彈協同制導的作戰應用具有一定的參考價值.需要指出的是，本文僅考慮了制導交接后的制導誤差，沒有對制導交接引入的誤差進行分析，下一步需要對不同制導交接條件下的制導精度進行建模研究.

[1]高堅，佟明安.雙機編隊協同制導的火控機理[J].火力與指揮控制，2009，34（12）：38－40.GAO Jian，TONG Ming－an.Fire control principle on cooperative guidance with two－fighters team[J].Fire Control ＆ Command Control，2009，34（12）：38－40.（in Chinese）

[2]肖冰松，方洋旺，許蘊山.雙機協作發射與制導中程空空導彈技術研究[J].電光與控制，2009，18（2）：13－16.XIAO Bing－song，FANG Yang－wang，XU Yun－shan.Technologies for dual－fighter’s cooperative launching and guiding of medium range air－to－air missiles[J].Electronics Optics ＆ Control，2009，18（2）：13－16.（in Chinese）

[3]肖冰松，方洋旺，胡詩國.多機空戰協同制導決策方法[J].系統工程與電子技術，2009，31（3）：56－60.XIAO Bing－song，FANG Yang－wang，HU shi－guo.Decision methods for cooperative guidance in multi－aircraft air warfare[J].Systems Engineering and Electronic，2009，31（3）：56－60.（in Chinese）

[4]刁興華，方洋旺，王鵬.對地攻擊協同制導決策方法[J].電光與控制，2011，18（3）：52－55.DIAO Xing－hua，FANG Yang－wang，WANG Peng.Cooperative guidance decision－making in air－to－ground attacking[J].Electronics Optics ＆ Control，2011，18（3）：52－55.（in Chinese）

[5]ZHAO Shi－yu，ZHOU Rui.Cooperative guidance for multi－missile salvo attack[J].Chinese Journal of Aeronautics，2008，21：533－539.

[6]牛曉川，陳少華，吳宗一，等.協同制導條件下空空導彈中末制導交接班能力[J].彈箭與制導學報，2011，31（4）：41－45.NIU Xiao－chuan，CHEN Shao－hua，WU Zong－yi，et al.Investigation of air－to－air missile’s midcourse and terminal guidance handing－off based on cooperative guidance[J].Journal of Projectiles，Rockets，Missiles and Guidance，2011，31（4）：41－45.（in Chinese）

[7]周志剛.航空綜合火力控制原理[M].北京：國防工業出版社，2008.ZHOU Zhi－gang.Synthesis fire control principle for aviation[M].Beijing：National Defense Industry Press，2008.（in Chinese）

[8]付海峰，劉華偉，張宗麟.中距主動制導空空導彈目標截獲概率仿真計算[J].電光與控制，2007，14（3）：55－58.FU Hai－feng，LIU Hua－wei，ZHANG Zong－lin.Simulated computation of target－acquisition probability of medium－range active－guided AAM[J].Electronics Optics ＆ Control，2007，14（3）：55－58.（in Chinese）