模糊控制在污水技術評估實驗室溫控系統中的應用
張偉,許春蓮* ,黃海明,馬愛君,武少偉
1.中國環境科學研究院,北京 100012
2.山東電子職業技術學院,山東 濟南 250200
為適應我國環境保護技術的快速發展,有效提升環境保護能力,開展了水污染防治生物技術實驗室驗證評估。通過對生物處理新技術全面客觀的驗證評估,可以有效地進行新技術推廣,推動環保技術的創新發展。在實驗室驗證評估過程中,為滿足微生物的生存需要,驗證評估用的原水需具有適當和穩定的溫度。按照工藝流程,來自居民樓的生活污水首先經格柵處理后與冷凍液進行熱交換,變為5℃的實驗用原水,然后通過加藥進行水質調整,使水質保持在穩定的范圍內,進入污水處理設備前需經過與65~80℃熱水進行熱交換使水溫達到13~20℃,以滿足驗證評估客觀性和科學性的要求。
由于溫度控制系統具有不確定、非線性、大滯后等特點,常規的PID控制難以滿足驗證評估所需原水溫度控制要求[1]。1964年美國的Zadeh教授創立了模糊集合理論,1974年英國的Mamdani研制出第一臺模糊控制器。模糊控制器不需要了解對象的精確數學模型,根據專家知識進行控制,用模糊控制器實現對溫度控制系統的控制,大大改進了原系統的控制效果,在一定程度上滿足了系統快速性的要求[2-6]。針對生物處理技術實驗室驗證評估過程中原水升溫控制系統,筆者設計了一種自適應模糊控制器,根據溫控系統中熱交換器后原水溫度的反饋,通過模糊規則推理和決策,在線整定控制參數,以實現對驗證評估用原水溫度的自適應控制。
1 原水溫度控制系統
水污染防治生物處理技術實驗室驗證評估過程中,進入生物技術處理流程的原水應具有合適、穩定的溫度。收集于生活區的原水經過低溫儲存、水質調整,與鍋爐提供的熱水通過熱交換器,水溫升至驗證所需的溫度后,直接進入生物技術處理流程,開始驗證評估工作。溫度控制系統主要是保證原水出水有恒定的預設溫度,控制元件是熱水調節三通閥,該閥門控制流經交換器熱水的流量,將預設定的原水溫度作為給定值,經熱交換后原水的溫度作為反饋值,閥門的開度作為輸出值,以保證流入生物技術處理單元的原水溫度的恒定。原水溫度控制系統原理如圖1所示。

圖1 溫度控制系統原理Fig.1 The principle diagram of temperature control system
2 模糊控制器設計
由于被控對象的復雜性(非線性),難以建立精確的數學模型,因此,有關被控對象的知識主要來源于領域專家或操作人員的知識和經驗。針對驗證評估中的溫度控制系統,通過控制原理可以確定基本控制策略。因此設計一種自調整模糊控制器,可實現動態和穩態性能很好的控制。模糊控制器結構如圖 2 所示[7-9]。
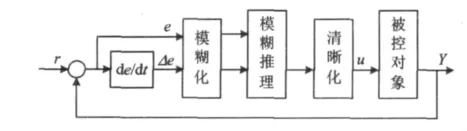
圖2 模糊控制器結構Fig.2 The structure diagram of fuzzy controller
在運行中不斷地檢測偏差和偏差變化率,將其輸入模糊控制器進行模糊化,運用模糊推理,進行模糊運算,對輸出控制量在線修改并清晰化,作用于被控對象,使被控對象具有良好的靜態及動態性能。模糊控制器的設計分為清晰量的模糊化、模糊控制規則和模糊量的清晰化三部分。
2.1 清晰量的模糊化
在模糊控制系統運行中,控制器的輸入值、輸出值是有確定數值的清晰量,而在進行模糊控制時,模糊推理過程是通過模糊語言變量進行的,因此需將物理量的清晰值轉換成模糊語言變量。
該控制器中各語言變量的論域設定如下:

為計算機處理方便且不影響仿真結果,在該控制器中論域E、EC及U等語言變量的隸屬函數取三角函數(圖3)。
2.2 模糊控制規則

圖3 E、EC及U的隸屬函數Fig.3 The membership function of E,EC and U
模糊控制規則是基于手動控制策略建立的,而手動控制策略又是人們通過學習、實驗以及長期經驗積累而逐漸形成的[3]。從系統的穩定性、響應速度、超調量和穩態精度等各方面考慮,根據過程模糊模型生成控制規則。當偏差較大時,對偏差給予較大權重,以盡快消除誤差,提高響應速度;當偏差較小時,為避免系統超調,對偏差變化率的影響給予較大的權重,以盡快進入穩態[10-12],據此生成模糊控制規則,如表1所示[2]。為表明論域E、EC及U之間的控制關系,根據模糊控制規則生成的模糊控制規則表面如圖4所示。

表1 模糊控制規則表Table 1 Regulations of fuzzy control
2.3 模糊量的清晰化
經過模糊推理決策,整定的輸出量要進行清晰化取得精確值以計算輸出控制量,即熱水調節電動閥的開度。常用的清晰化方法包括最大隸屬度法、重心法、中心平均法等。該控制器中采用中心平均法求取輸出量的精確值。
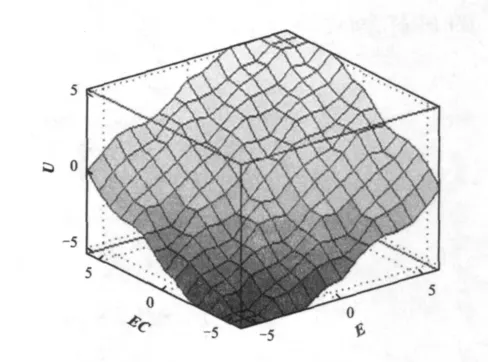
圖4 模糊控制規則表面Fig.4 Rules surface of fuzzy control
中心平均法既避開了求取隸屬函數的積分運算,同時又考慮了各模糊集合對精確值的影響。該方法計算較簡單,清晰化的魯棒性較好,是模糊推理系統中常用的方法[7]。中心平均去模糊化方法公式:
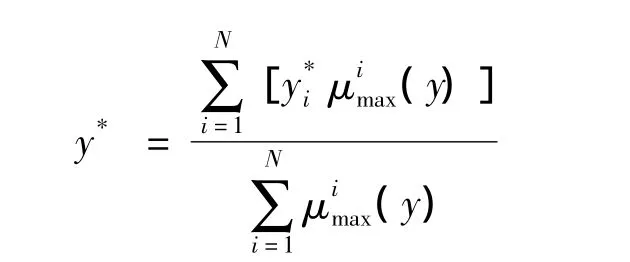
3 模糊控制器應用
熱交換器系統模型可以用純滯后環節和一階慣性環節表示。對于水污染防治生物處理技術實驗室驗證評估過程中的熱交換系統,函數模型可表示如下:
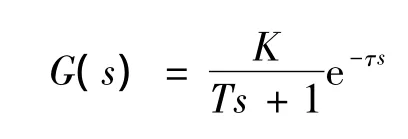
式中,K為增益系數,取值5;T為時間常數,取值3500 s;τ為滯后時間,取值200 s;s為時間變量。
在Matlab7.0工作環境下,利用模糊推理系統編輯器建立一個fis文件,定義為flc.fis。在Simulink仿真環境下,根據圖2的模糊控制器結構利用工具箱編輯系統框圖,輸入為偏差論域E和偏差變化率論域EC,輸出為溫控系統模型輸出,并增加積分環節與模糊控制器輸出進行疊加,以消除靜態誤差,然后與被控對象溫控系統的模型相連接,輸出反饋到控制器輸入端,得到控制器與一階滯后被控對象組成的控制系統仿真框圖,如圖5所示。

圖5 模糊自調整控制系統仿真Fig.5 Simulation block diagram of fuzzy self-adjustment control system
4 仿真結果與分析
在單位階躍輸入下,通過調整量化因子(kE,kEC)和控制增量比例因子(kU),可得到比較理想的模糊控制仿真結果。kE取值1.35,kEC取值0.98,kU取值1.05,kI取值0.0016。對積分環節采取限幅,該次仿真實驗中限幅為0.2。利用仿真參數對話框,設置相關的仿真參數,仿真時間設置為5000 s,采樣周期設置為1 s。對熱交換器分別采用常規PID控制器和模糊自調整控制器進行調節,其中PID控制器參數按臨界比例法[13]進行調整,兩種控制器系統的單位階躍響應如圖6所示。

圖6 兩種控制器系統的單位階躍響應Fig.6 Response of two control system on step signal
由圖6可知,利用模糊自調整控制器與比例積分環節控制量疊加后,可消除靜差,減小超調量,響應速度快,調節時間短。與常規PID控制器相比,模糊自調整控制器具有良好的快速性和魯棒性,提高了系統的動、靜態性能。
5 結語
針對大滯后的溫度控制系統,與常規PID控制器相比,采用模糊自調整控制器可以使系統的動態性能和穩態性能得到改善,具有良好的控制效果。但通過仿真結果可以看出,控制器缺乏較強的自適應能力,系統仍有一定的超調量。因此,在今后研究中考慮綜合神經網絡、遺傳算法的智能控制器,在線訓練模糊規則、調整量化因子等,以優化溫控系統的動態性能和魯棒性,實現控制目的。
[1]陶永華.新型PID控制及其應用[M].北京:機械工業出版社,2002.
[2]孫增圻.智能控制理論與技術[M].北京:清華大學出版社,2003.
[3]易繼鍇,侯媛彬.智能控制技術[M].北京:北京工業大學出版社,2003.
[4]YANG X H,LIU T R,SUN J.Optimal PID control of heat exchanger temperature[J].Advanced Materials Research,2011,204/205/206/207/208/209/210:21-24.
[5]PADHEE S,SINGH Y.A comparative analysis of various control strategies implemented on heat exchanger system:a case study[C]//Proceedings of the World Congress on Engineering:Ⅱ.London:International Association of Engineers,2010.
[6]MAIDI A,DIAF M,CORRIOU J.Optimal linear PI fuzzy controller design of a heat exchanger[J].Chemical Engineering and Processing,2008,47(5):938-945.
[7]MAZINAN A H,SADATI N.Fuzzy predictive control based multiple models strategy for a tubular heatexchanger system[J].Applied Intelligence,2010,33(3):247-263.
[8]ARTURO P,CLAUDIA R,KEVIN P,et al.On-line fuzzy-logicbased temperature control of a concentric-tube heat exchanger facility[J].Heat Transfer Engineering,2009,30(14):1208-1215.
[9] ?AHIN ?ENCAN A,KILI? B,KILI? U.Optimization of heat pump using fuzzy logic and genetic algorithm[J].Heat and Mass Transfer,2011,47(12):1553-1560.
[10]MAZINAN A,SADATI N.Fuzzy multiple models predictive control of tubular heat exchanger[C]//2008IEEE World Congress on Computational Intelligence. Piscataway:IEEE Press,2008:1845-1852.
[11]HABBIA H,KIDOUCHEA M,KINNAERTB M,et al.Fuzzy model-based fault detection and diagnosis for a pilot heat exchanger[J].International Journal of Systems Science,2011,42(4):587-599.
[12]TABATABAEE S,ROOSTA P,SADEGHI M S,et al.Fuzzy PID controller design for a heat exchanger system:the energy efficiency approach[C]//International Conference on Computer Applications and Industrial Electronics(ICCAIE). Los Alamitors:IEEE Computer Society Press,2010:511-515.
[13]李園,李平.填料塔熱交換系統的模糊模型PID優化控制[J].工業儀表與自動化裝置,2006(5):50-53.○

