不確定性超混沌系統的自適應魯棒反同步

李鐘慎，傅桂元，楊凱

（華僑大學 機電及自動化學院，福建 廈門 361021）

不確定性超混沌系統的自適應魯棒反同步

李鐘慎，傅桂元，楊凱

（華僑大學 機電及自動化學院，福建 廈門 361021）

針對一類具有外部不確定性的反同步問題，提出一種自適應魯棒控制方法.基于Lyapunov穩定性理論和自適應控制，設計自適應魯棒控制器和參數的自適應更新律；通過在輸入控制量中引入一補償項以消除不確定性的影響，實現自適應魯棒反同步，將系統的反同步誤差控制在任意小的范圍內.最后，通過數值仿真驗證所提出控制方法的有效性.

超混沌系統；反同步；自適應；魯棒控制；不確定性

同步是指具有相近或相同性質的兩個或多個動力系統，通過系統間的相互作用，使得在不同的初始條件下各自演化的動力系統其狀態逐步接近，最后達到全同的狀態，它是自然界的一種常見的現象［1］.自Pecora和Corroll關于混沌同步的開創性工作［2］以來，混沌同步得到了廣泛而深入的研究 .在諸多混沌同步中，反同步也是一個值得關注的現象.所謂反同步就是兩個混沌系統的狀態變量的絕對值相同但符號相反，即狀態變量的和為0的同步現象［3］.超混沌系統一般為具有一個以上正的Lyapunov指數的混沌系統，具有比低維混沌系統更加復雜的動力學特性，使得實現超混沌的控制、同步（反同步）問題成為一項更具有挑戰性的研究工作［4］.文獻［5］提出了一種基于主動控制和自適應控制相結合的方法，實現對在參數已知和參數未知兩種情況下的兩超混沌系統的反同步控制.文獻［6］基于非線性控制實現兩不同結構超混沌系統的反同步.但是，至今含有不確定性的超混沌系統的反同步問題的研究較少，而現實應用中不可避免要受到各種外部不確定性的影響 .因此，研究一類不確定性超混沌系統的反同步問題具有重要的意義.本文設計一種自適應魯棒反同步控制器，實現一類具有外部擾動不確定性異結構超混沌系統的反同步.

1 問題描述

考慮驅動混沌系統具有的形式為

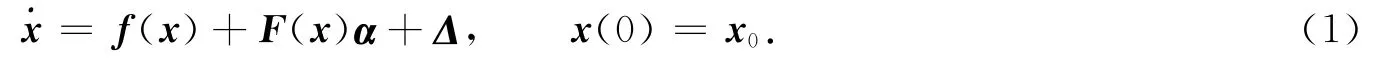
式（1）中：系統狀態變量x∈Rn；x0為初始值；未知參數α∈Rm；f（x）為n×1矩陣；F（x）為n×m 矩陣，且Fi，j（x）∈L∞；不確定性項Δ＝［Δ1，Δ2，…，Δn］T為n×1矩陣.假定不確定性項有界，且滿足‖Δi‖≤ρi（i＝1，2，…，n ），ρi為已知常數，則記ρ＝［ρ1，ρ2，…，ρn］T.

考慮響應混沌系統的形式為

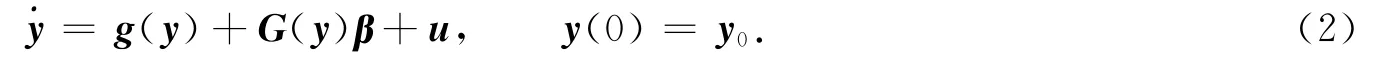
式（2）中：系統狀態變量y∈Rn；y0為初始值，且x0≠y0；未知系統參數β∈Rq；g（y）為n×1矩陣；G（y）為n×q矩陣；且Gi，j（y）∈L∞；u∈Rn為系統的控制輸入.

定義反同步誤差e＝y＋x，設計控制器u的控制目標是使反同步誤差e滿足

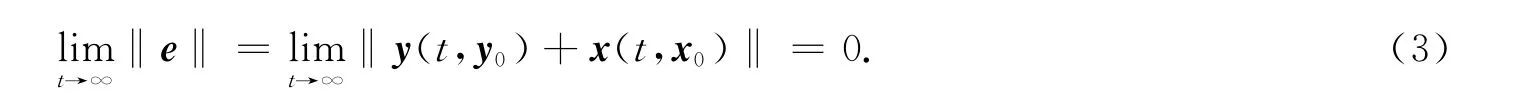
2 反同步控制器設計

將式（1）與式（2）相加，可得系統的反同步動態誤差方程為

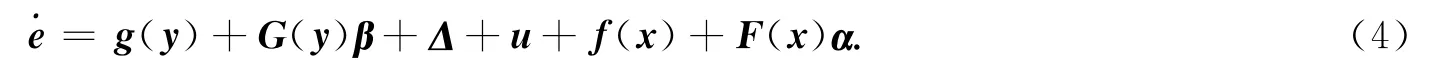
將式（5）沿動態誤差系統（4）對時間求導，則可得

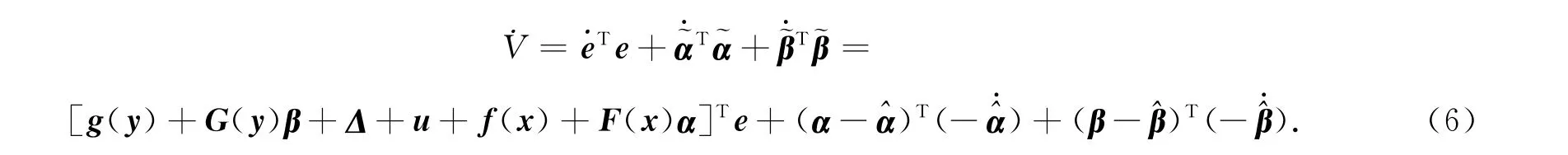
當選取控制器u為

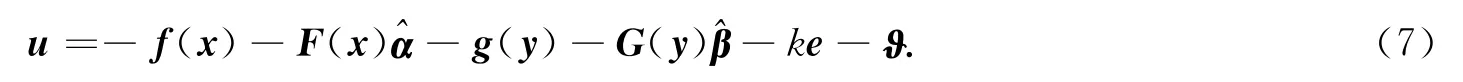
系統參數的自適應律為

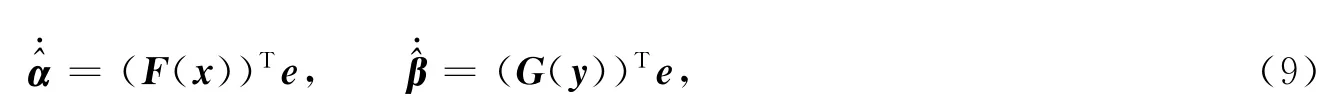
則式（6）可寫成如下形式，即

根據Young不等式

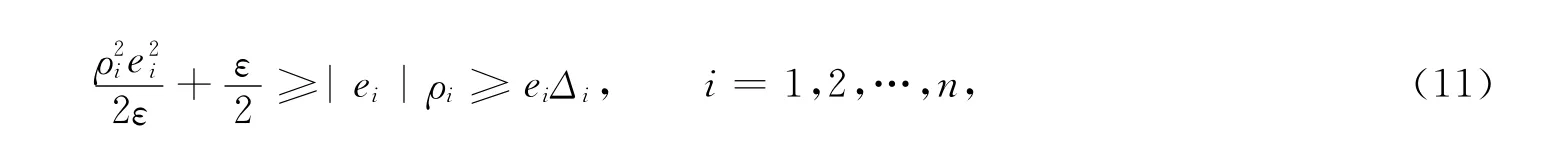
則式（10）可改寫為

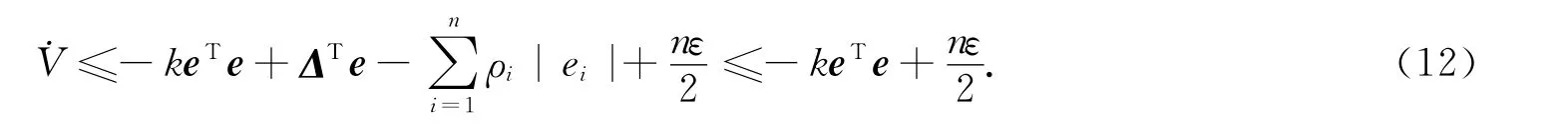
令Γ＝eTe，則Γ≥0.由于ε和k為任意正數，則總是存在ε和k，使得其滿足：對?Γ＞0，有此時˙V＜0.因此，系統（4）將漸近穩定于狀態空間原點，系統的誤差將處在以為半徑的圓內，可以通過選取適當的ε，k值，使誤差趨近于無窮小.此時，有

因此，對于被控動態誤差系統（4），當采用式（7），（8）所示的控制器及式（9）所示的參數自適應律，則系統將漸近趨于零平衡點，即響應系統（2）將漸近反同步于驅動系統（1）.

3 仿真實例

以超混沌Chen系統［7］和超混沌Lü系統［8］為例，通過數值仿真驗證該控制方法的有效性.

3.1 系統描述

假定超混沌Chen系統為驅動系統，寫成式（1）的形式，則可描述為

式（13）中：Δ＝［Δ1，Δ2，Δ3，Δ4］T為系統的外部擾動不確定性項，且Δi界限為已知，假定其值為Δ＝［0.25sin（0.25πt），0.8cos（0.5πt），0.9sin（0.6πt），2cos（3πt）］T，則可得其界限ρ＝［0.25，0.8，0.9，2］T.

選取超混沌Lü系統為響應系統，寫成式（2）的形式，即

式（14）中：u＝［u1，u2，u3，u4］T為系統的控制輸入.當選取系統參數a1＝35，b1＝3，c1＝12，d1＝7，r1＝0.5時，系統（13）表現為超混沌系統特性；而當選取系統參數a2＝36，b2＝3，c2＝20，r2＝1時，系統（14）在未施加控制u 的表現為超混沌系統.系統參數的估計值＾α＝［＾a1，＾b1，＾c1，＾d1，＾r1］T，＾β＝［＾a2，＾b2，＾c2，＾r2］T.

定義系統的反同步誤差定義誤差為

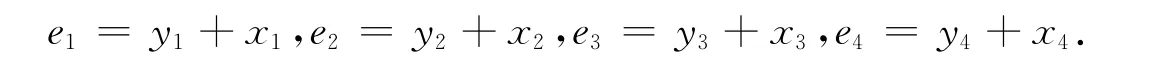
由式（13）和式（14）可得反同步誤差動態系統為

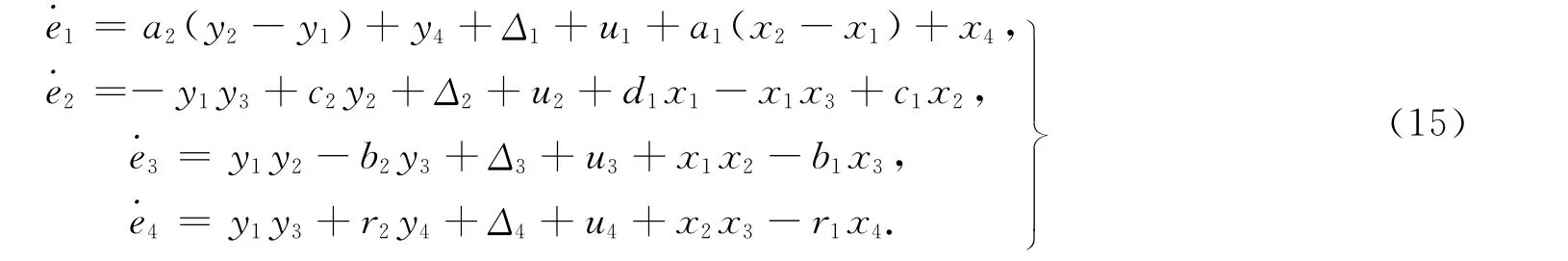
根據式（7），（8），（9）可得自適應魯棒控制器為

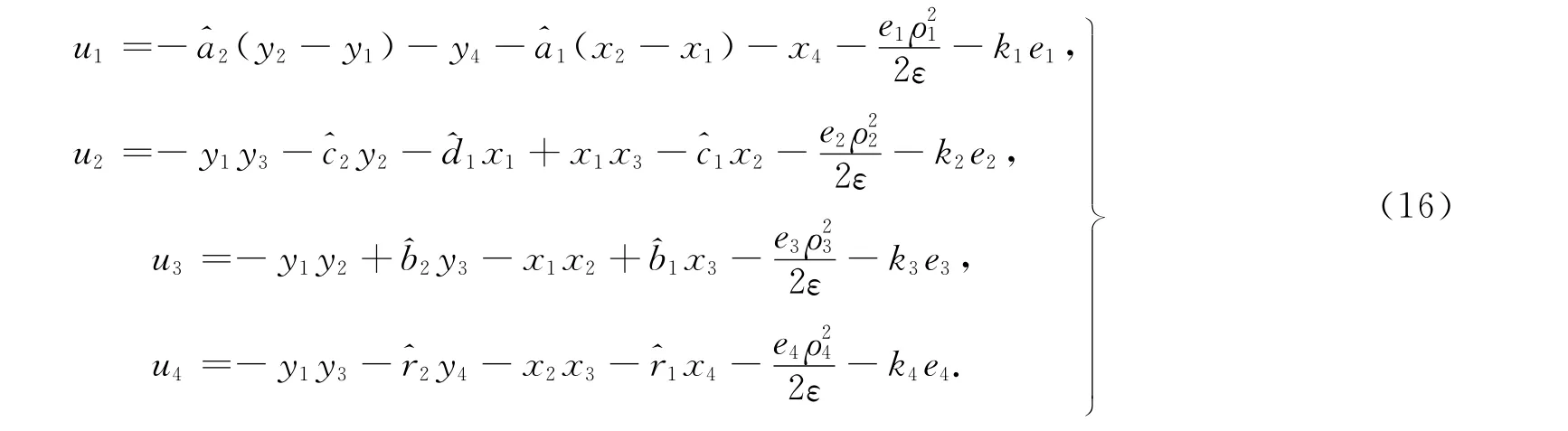
式（16）中：ki＝k（i＝1，2，3，4），ε均為任意大于零的常數.系統參數的自適應律為

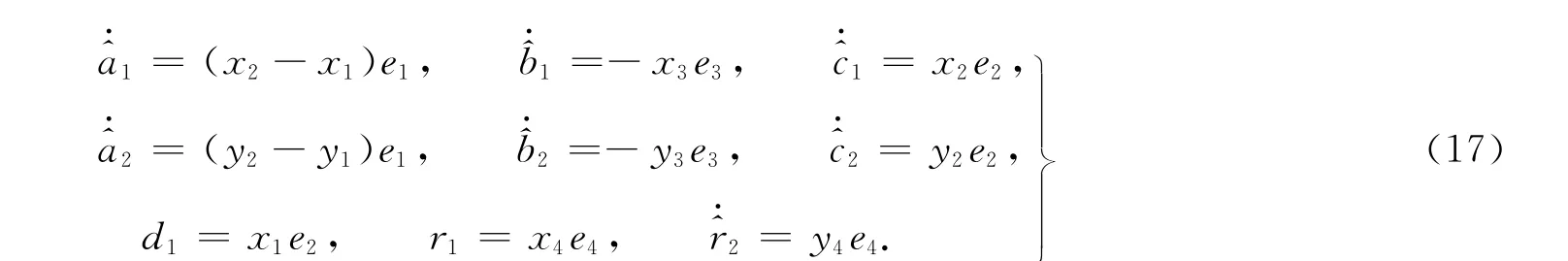
3.2 仿真結果

選取超混沌Chen系統各狀態變量初值x1（0）＝－2，x2（0）＝－3，x3（0）＝8，x4（0）＝10；超混沌Lü系統各狀態變量的初值y1（0）＝5，y2（0）＝8，y3（0）＝－1，y4（0）＝－3，則反同步動態誤差變量的初值為e1（0）＝3，e2（0）＝5，e3（0）＝7，e4（0）＝7，參數估計初值＾α（0）＝［4，6，8，10，3］T，＾β（0）＝［5，7，9，11］T；系統的設計參數k＝5，ε＝0.001.

超混沌Chen系統（13）、超混沌Lü系統（14）的反同步各狀態變量的時間響應曲線、反同步誤差曲線及各參數的估計值，分別如圖1，2，3所示 .從圖2中可以看出：在控制器（16）的作用下，系統的反同步誤差信號快速趨近于零.從圖3可知：隨著時間t的推移，系統的未知參數也逐漸收斂于穩定值.

圖1 超混沌系統各狀態變量的時間響應曲線Fig.1 Curve about time response of each state of the hyperchaotic systems

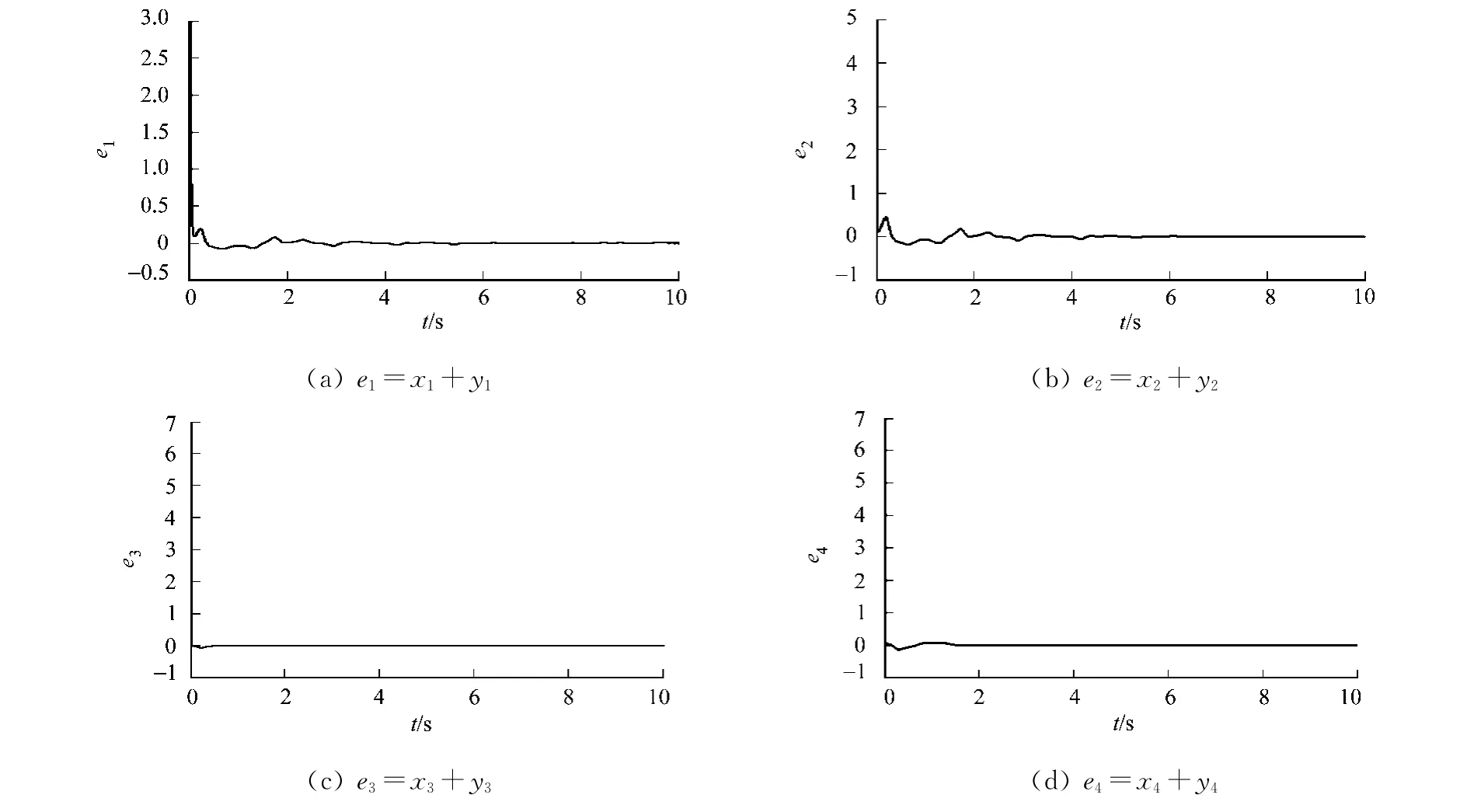
圖2 超混沌系統的反同步誤差曲線Fig.2 Curve of the anti－synchronization error of the hyperchaotic systems

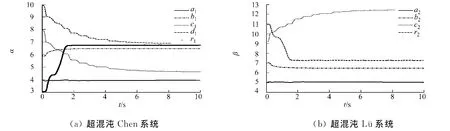
圖3 超混沌系統各參數的估計值Fig.3 Estimated value of the parameters of the hyperchaotic systems

4 結束語

研究一類具有外部擾動不確定性的不同結構超混沌系統的魯棒自適應反同步問題.基于穩定性理論和自適應控制，設計一種改進的魯棒自適應控制器，通過加入補償器，消除了不確定性的影響，從而實現系統的反同步及系統未知參數的辨識.通過選擇適當的設計參數ε，k，使系統反同步誤差趨于無窮小.以超混沌Chen系統和超混沌Lü系統為例，數值仿真結果證明了所提出的控制策略的有效性及具有較強的魯棒性.該控制方法應用范圍廣泛，響應速度較快.

［1］傅桂元，李鐘慎.無源控制的超混沌Chen系統的自適應同步［J］.華僑大學學報：自然科學版，2010，31（4）：378－382.

［2］PECORA L M CARROLL T L.Synchronization in chaotic systems［J］.Phys Rev Lett，1990，64（8）：821－824.

［3］朱少平.不確定超混沌系統的反同步研究［J］.計算機工程與應用，2011，47（10）：145－145，175.

［4］劉福才，李俊義，臧秀鳳.基于自適應主動及滑模控制的分數階超混沌系統異結構反同步［J］.物理學報，2011，60（3）：030504（1－9）.

［5］WANG Zuo－lei.Anti－synchronization in two non－identical hyperchaotic systems with known or unknown parameters［J］.Commun Nonlinear Sci Numer Simulat，2009，14（5）：2366－2372.

［6］Al－SAWALHA M M，NOORANI M S M.Anti－synchronization of two hyperchaotic systems via nonlinear control［J］.Commun Nonlinear Sci Numer Simulat，2009，14（8）：3402－3411.

［7］LI Yu－xia，TANK W K S，CHEN Guan－rong.Generating hyperchaos via state feedback control［J］.Int J Bifurcat Chaos，2005，15（10）：3367－3375.

［8］CHEN Ai－min，LU Jun－an，LüJin－hu，et al.Generating hyperchaotic Lüattractor via state feedback control［J］.Physica A，2006，364：103－110.

Self－Adaptive Robust Anti－Synchronization of Hyperchaotic Systems with Unicertainties

LI Zhong－shen，FU Gui－yuan，YANG Kai

（College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361021，China）

A novel self－adaptive robust control method is proposed to anti－synchronize a kind of hyperchaotic systems with different structures and external uncertainties.Based on Lyapunov stability theory and adaptive control，a self－adaptive robust controller is designed and the updating laws of unknown parameters are given as well.The self－adaptive antisynchronization is achieved by adding a compensator into the input to eliminate the influence of uncertainties，and the anti-synchronization error of a system is bounded within an arbitrarily small value.Numerical simulations are provided to demonstrate the effectiveness of the presented control scheme.

hyperchaotic system；anti－synchronization；self－adaption；robust control；uncertainty

O 19；TP 13

A

1000－5013（2012）02－0129－05

2011－08－11

李鐘慎（1971－），男，教授，主要從事先進控制理論與控制工程的研究.E－mail：lzscyw＠hqu.edu.cn.

福建省自然科學基金計劃資助項目（2011J01350）；華僑大學基本科研業務費專項基金資助項目（JBZR1107）

（責任編輯：黃曉楠 英文審校：鄭亞青）