極限運算方法研究
2013-01-11 09:11:30朱美玲
太原城市職業技術學院學報 2013年1期
朱美玲
(太原城市職業技術學院,山西 太原 030027)
極限的求解是高等數學基本運算之一,其包含的類型多,方法技巧性強,論文介紹幾種求極限常用的方法。
一、直接代入
初等函數在其定義域內某點的極限等于函數在該點的函數值,即求連續函數的極限,可歸結為計算函數值。
二、消去零因子
1.分解因式
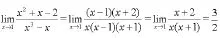
2.通分
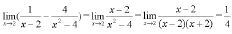
3.有理化
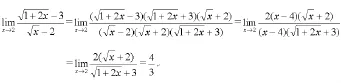
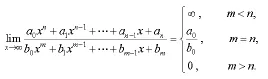
三、比較次數
其中,a0≠0,b0≠0。
四、無窮小
1.無窮小與有界函數的積仍是無窮小
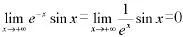
2.利用無窮小與無窮大的倒數關系
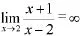
3.等價無窮小代換
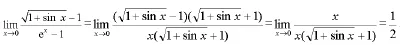
(當 x→0時,ex~x,sin x~x)
五、利用重要極限求極限
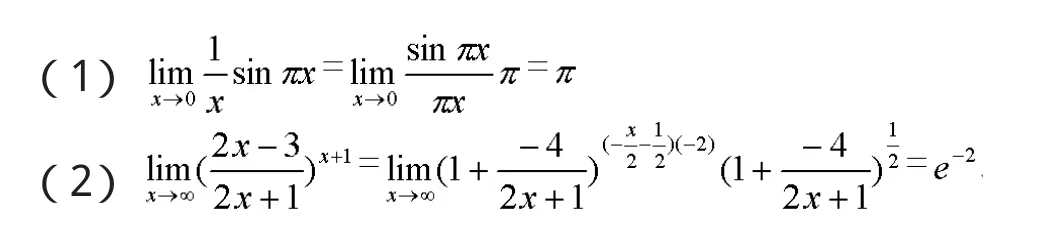
六、洛比達法則求極限
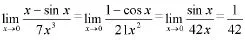
七、夾逼準則求極限
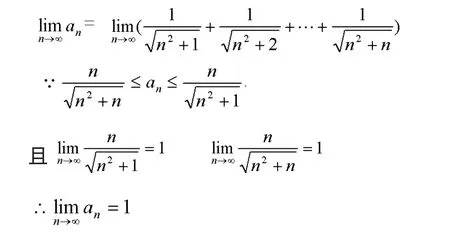
八、定積分求極限
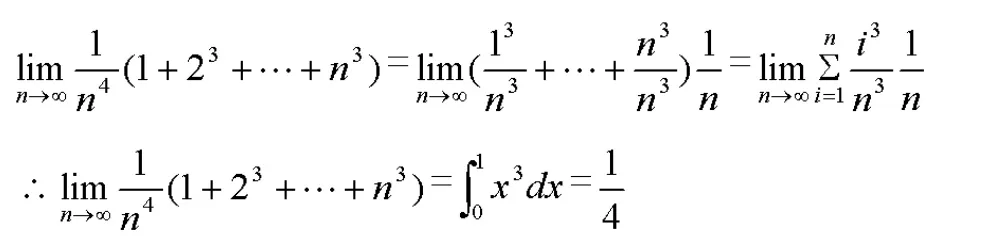
此外,還有利用泰勒公式求極限、柯西準則求極限等等。總之,求極限方法靈活多變,只有通過大量練習、及時總結,才能在解題當中根據題型迅速選擇適當方法準確求解。
[1]葉志萍.洛比達法則運用中的弱點克服[J].大連民族學院學報,2002,(2).
[2]岳衛芬.利用極限的除法法則求f(x)/g(x)型的極限[J].高等函授學報(自然科學版),2005,(6).
猜你喜歡
中等數學(2022年2期)2022-06-05 07:10:50
中學生數理化·七年級數學人教版(2021年11期)2021-12-06 05:38:48
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
兒童故事畫報(2019年5期)2019-05-26 14:26:14
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
數學小靈通·3-4年級(2017年6期)2017-06-22 11:28:50
Coco薇(2016年2期)2016-03-22 02:42:52
Coco薇(2015年1期)2015-08-13 02:47:34
小雪花·成長指南(2015年7期)2015-08-11 15:03:12

