落體偏東在慣性系中的分析

王灑 王玲 汪志云

(湖北文理學院物理與電子工程學院 湖北 襄陽 441053)

在大學物理教學中，落體偏東是一個耐人尋味的問題，在這個問題上很多學生百思不得其解．理論力學教材中，關于落體偏東計算公式的推導多采用轉動坐標系求解，從而得到如下微分方程組(1).然而，對這個問題用非慣性系并以科里奧利力來解釋落體的偏東實在是沒有必要．無論是從轉動坐標系本身涉及的復雜計算，還是從整個過程對落體偏東本質的闡釋來看，這種方法其實都并沒有起到促進教學的效果．

本文將采用靜止坐標系來分析落體偏東的本質，并在慣性坐標系中推導落體偏東計算公式．

1 落體偏東問題在轉動坐標系中的表述

轉動坐標系中落體的運動微分方程為[1]

(1)

式中，ω為地球自轉的角速度，λ為地面上的緯度，h為落體距地面的高度.代入初始條件

(2)

由于ω=7.3×10-5rad/s，略去數值較小的含ω2項積分得到

(3)

上式即為一般理論力學教材中關于落體偏東數值的計算式.

2 慣性坐標系中的落體偏東問題

我們知道，初始高度為h0(h0?R，R為地球半徑)的自由落體都有

(4)

以地球球心為原點，建立如圖1所示慣性坐標系O-xyz[2].

圖1 慣性系中的落體

由圖1中幾何關系不難看出，落體到地軸的距離r也是時間的函數[3]

(5)

由于地球對落體引力為有心力，且地軸穿過地心，則對地軸l動量矩守恒[4]

(6)

則有

(7)

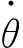
由于h0-h?h+R，故有

(8)

(9)

則落體較地表多轉過的角度為

而此過程中地表也以地軸為軸轉動，忽略落體下落后在緯度方向的位移(這個值極小)，落體任意時刻的偏東微分數值為[5]

ds=(h+R)cosλdθ′=ω0gt2cosλdt

落體落地時有

代入得到整個過程中的偏東值

(10)

這與轉動坐標系中的結果是相符的．

3 結論

在轉動坐標系和慣性系中應用不同的分析方法最終得到相同的結果，然而比較兩種方法不難發現兩種方法的特點，在慣性系中的分析明顯具有簡單直觀的思路，使學生在思維層面上更易于接受．

在慣性系中分析落體偏東問題更為直觀：地球和落體之間為有心力的作用，就可以借助動量矩守恒來分析，以轉動角代替直接的偏東位移，這一點在教學中是值得借鑒的．因為落體偏東的本質是落體高度下降后角速度增大(動量矩守恒)的結果，這就意味著任意時刻將比地面轉過更大的角度，如果學生看清了這一點，落體偏東就成為一種直觀的必然，而不會產生由科里奧利力和轉動坐標系的分析了帶來的神秘感．

不僅如此，也可以讓不具備轉動坐標系相關知識的高中生接觸和了解，降低了接受的難度．

參考文獻

1 周衍柏.理論力學.北京：高等教育出版社,2012.189～191

2 程緒和.關于落體偏東問題的討論.安慶師范學院學報，1982(1):59～61

3 梁昆淼.落體偏東的初等解說. 大學物理，1984(2):1～2

4 閻鳳麗.在地心參照系中對地球赤道上落體偏東的計算.大學物理，1994(1)：26～27

5 劉嘉斌.在慣性系中分析落體偏東現象.工程物理，1998(5):17