靜電場中的幾個物理公式與其物理模型
董梅峰 宋新祥
(中國石油大學 山東 青島 266555)
物理規律是對客觀自然規律的描述,而對客觀自然規律描述之前往往需要建立一個與其對應的物理模型.物理規律的描述一般有兩種,一種是文字描述,另一種是數學描述,而物理規律的最終的也是最完美的描述形式是用數學公式來描述.所以物理規律的描述往往離不開數學公式,而一旦用數學公式來描述物理規律,這個數學公式就有了物理意義,公式中的各個物理量都有一定物理意義,其取值也要保證有物理意義,如果物理量的數學取值導致該公式沒有物理意義了,此公式也就不成立了,此時該公式對應的物理模型發生了變化,所以需要尋找對應新模型的數學表達公式了.下面看幾個典型的例子.
1 點電荷的電場強度公式的理解
點電荷激發的場的數學表達公式是靜電場中的一個基本公式,即

(1)
公式中的r是場點到點電荷的距離,在數學上如果r→0,則電場強度的大小E→∞,這在物理上是沒有物理意義的.出現這種情況也就是說公式(1)不適用于r→0時所對應的物理模型,同時也說明了r→0時的物理模型不再是“點電荷”的物理模型了.回顧一下“點電荷”物理模型的建立條件,就不難理解當r→0時,帶電體的形狀和大小相對于場點而言就不能忽略了,此時帶電體就不能視為“點電荷”物理模型了,所以上述公式不再適用了.
考慮到實際的帶電體,當r→0時,場點在何處呢?不難理解此時場點已經到了帶電體內部了.此時可以理解為物理模型由點電荷變為均勻帶電的球體,如果其總的帶電荷量為q,電荷體密度為ρ,可以用高斯定理很容易得到在均勻帶電球體內、外的電場強度公式分別為

(2)
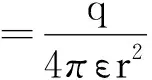
(3)
由式(2)可知當r→0時,E內→0,這樣就有物理意義了.
2 無限長的均勻帶電直線的電場強度公式的理解
無限長的均勻帶電直線激發的場的數學表達式為
(4)
公式中的r是場點到無限長的均勻帶電直線的垂線距離,在數學上如果r→0,則電場強度的大小E→,這在物理上也是沒有物理意義的.此時考慮到實際的帶電體,當r→0時,場點在何處呢?不難理解此時場點也已經到了帶電體內部了.此時可以理解為模型變為無限長的均勻帶電的圓柱體,如果其半徑為R,單位長度上的帶電荷量仍為λ,由高斯定理可求出其內、外的場強分布為

(5)
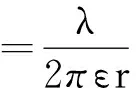
(6)
由公式(5)可知當r→0時,E內→0,這樣就有物理意義了.
3 計算點電荷和無限長均勻帶電直線激發的場的能量
3.1 點電荷激發的場的能量
由能量密度的體積分可得電場的能量,即
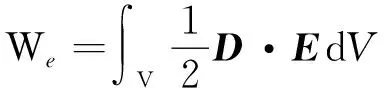
(7)
公式中D=εE,把點電荷的場強公式(1)代入公式(7)得
很明顯上述積分結果又趨于無窮大,在物理上又沒有物理意義了,而式(7)適用于任何帶電體激發的場.此時同樣回顧“點電荷”的物理模型的建立條件就明白,在上述積分公式中的積分下限為零時,此物理模型就不再是“點電荷”的物理模型了.如果考慮到實際情況,當r→0時,場點已經到了帶電體內部了.把式(2)、(3)代入式(7)積分物理意義就明確了.
3.2 無限長均勻帶電直線激發的場的能量
由式(7)可得一長度為L,可視為無限長的,線電荷密度為λ的無限長均勻帶電直線激發的場的能量為
很明顯上述積分結果也沒有實際物理意義,從上述公式的積分下限看,考慮到實際情況,當r→0時,場點已經到了帶電體內部了.上述帶電“直線”的模型就不成立了;從上述公式的積分上限看,考慮到實際情況,當r→時,長度為L的直線就不能視為“無限長”的了.總之上述公式的積分上限和下限所描述的物理模型已不再是“無限長的均勻帶電直線”的物理模型了,所以其積分結果也不是上述物理模型所激發的場的能量.
4 結論
通過以上數學公式與其所對應的物理模型的關系可以看出,物理模型不同,用數學語言描述其所遵循的物理規律也就不同,所以每個物理上的數學公式都有其物理意義,也就是描述了一個物理模型所遵循的物理規律.通過以上例子進一步明確了物理上數學公式的物理意義,以及在物理上建立物理模型具有重要的意義.有了建立物理模型的思路,這對物理規律的理解以及物理規律數學表達形式的理解都有很大的幫助.
參考文獻
1 賈瑞皋.大學物理教程.北京:科學出版社,2009. 10~11
2 賈瑞皋.電磁學.北京:高等教育出版社,2003.13

