范德瓦耳斯氣體直線過程的若干討論

張金榮 劉應開

(云南師范大學物理與電子信息學院 云南 昆明 650500)

1 引言

大家熟知，理想氣體經歷的熱力學準靜態過程(如等壓過程、等溫過程、等容過程、絕熱過程)的吸放熱特性是確定的.有人已經從dT,dQ討論了理想氣體直線過程中溫度的變化及吸放熱的情況[1]，并利用dS確定了熵的極大值點[2].文獻[3]中作者從理想氣體直線過程中態函數溫度和熵與狀態參量體積的關系式出發，采用了數學求極大值方法確定了理想氣體直線過程中溫度最高點M和吸放熱的轉換點N的狀態參量.后來有人又從斜率變化的角度研究了理想氣體直線過程的斜率與吸放熱特性的關系[4].但是具體每個過程吸熱多少，外界對其做功的關系仍不清楚.由于理想氣體的特殊性，文獻[5]討論了與實際氣體較為接近的范德瓦耳斯氣體的內能、熵[5,6]以及準靜態過程中吸放熱轉變點的求解方法[7]等進行研究、討論.然而，對于范德瓦耳斯氣體在直線過程中相關特性的研究卻未見報道.為此，本文從理論上推出1 mol的范德瓦耳斯氣體在直線過程中的溫度轉換點以及吸放熱轉換點，隨后計算了各種氣體在該直線過程中對應的溫度以及熱量轉換點，找到了影響溫度以及熱量轉換點的因素，并且利用Matlab繪出了(T,k,V)和(Q,k,V)三維空間圖，直觀反映出溫度及吸放熱特性隨著斜率、體積的變化關系.

2 M點的狀態參量和過程溫度的變化情況

為了方便，文中討論了1 mol的范德瓦耳斯氣體在直線過程中相關過程進行討論.直線過程AB(A為初始態，B為終態)斜率為k，截距為b，其過程方程為

p=k1V+b1

(1)

上式中k1<0,b1>0，其p-V關系如圖1所示.

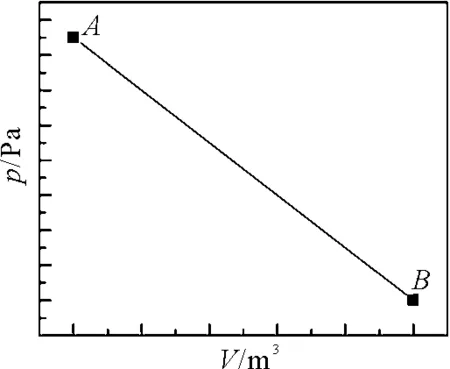
圖1 直線過程AB的p-V圖

范德瓦耳斯氣體的狀態方程為

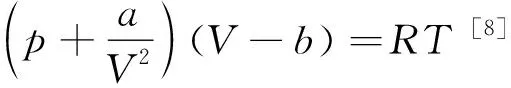
(2)

把式(1)代入式(2)，可得

(3)

式(3)即為溫度隨著體積的變化關系式

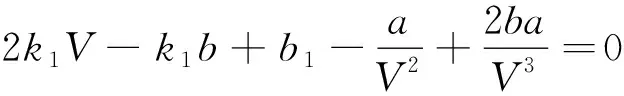
(4)

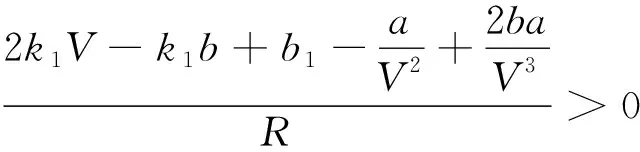
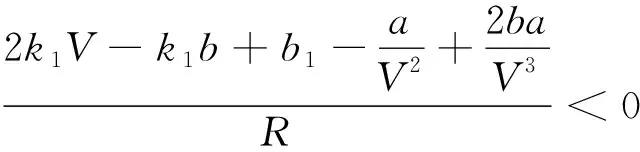
式(4)兩邊同時乘以V3得

2k1V4+(b1-k1b)V3-aV+2ba=0

這是一個關于V的代數方程，如果已經知道直線的斜率、截距和氣體的種類，利用Matlab的求根函數roots即可求出該氣體沿著這條直線變化時溫度的轉變點.

2.1 實例討論

假設n=1 mol的氣體沿著如圖2所示的直線過程變化，其中A為起始狀態，B為終止態.

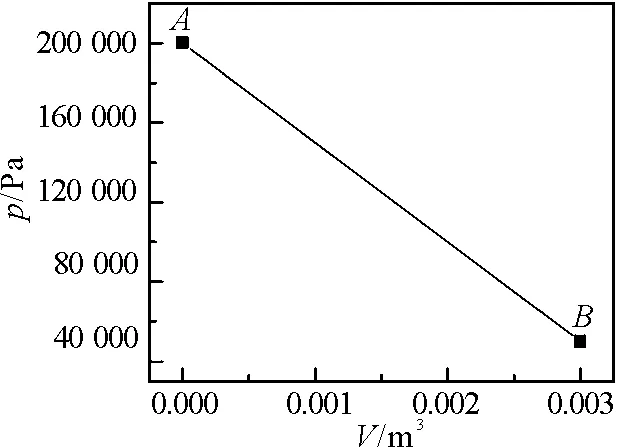
圖2 直線過程AB的p-V圖

該直線過程的數學方程為

p=-0.5*108V+2*105

(5)

表1氣體的范德瓦耳斯系數以及定體摩爾熱容[8，9]

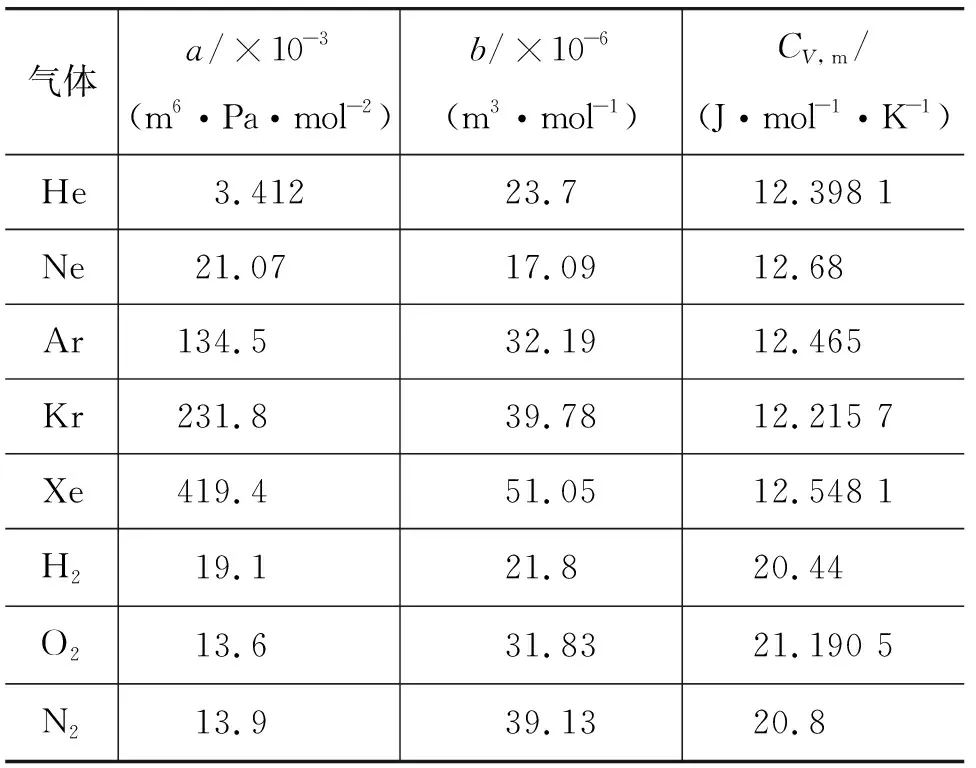
氣體a/×10-3(m6·Pa·mol-2)b/×10-6(m3·mol-1)CV,m/(J·mol-1·K-1)He3.41223.712.398 1Ne21.0717.0912.68Ar134.532.1912.465Kr231.839.7812.215 7Xe419.451.0512.548 1H219.121.820.44O213.631.8321.190 5N213.939.1320.8

下面我們根據表1分別求出各個氣體沿著該直線變化時溫度的轉變點M的體積(見表2).

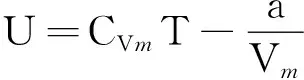
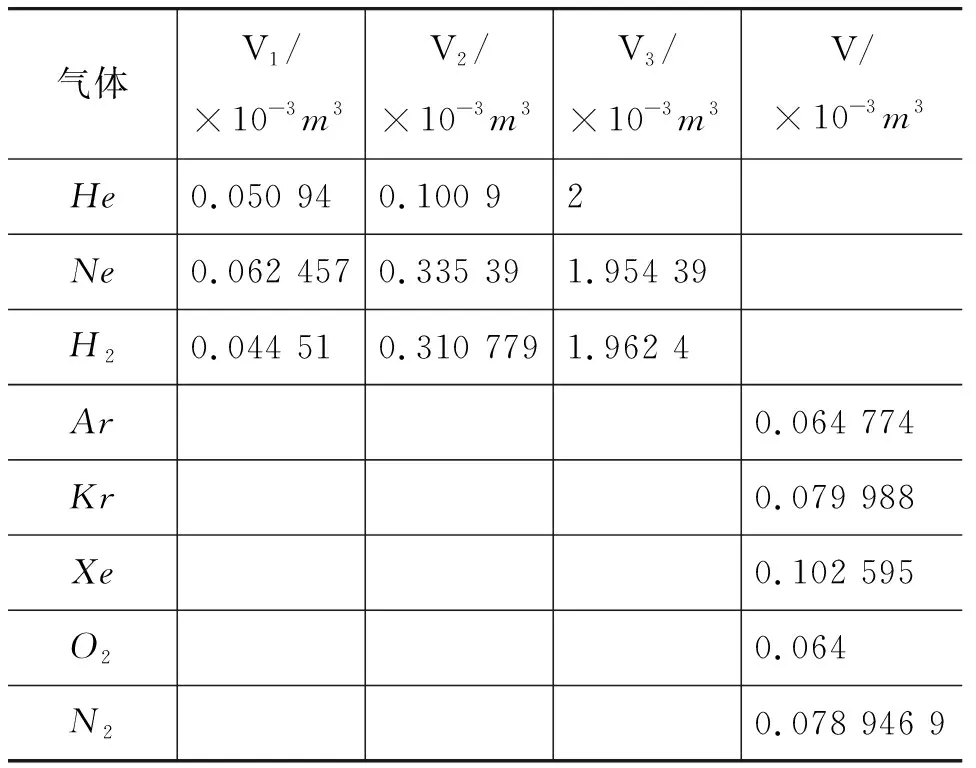
表2 溫度轉換點M的體積(氣體沿直線變化時)

2.2 溫度隨著斜率與體積的變化

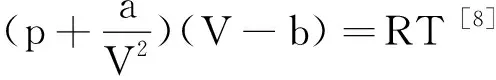
T=R-1[kV2+(p0-kV0-kb)V+

(6)

從式(6)可以看出,對于同種氣體而言,溫度僅僅由k和V確定，如果取原點作為直線的起點，則可以利用Matlab作出關于溫度、斜率和體積(T,K,V)的三維空間圖如圖3所示.

圖3中橫軸表示k,縱軸表示V,豎軸表示T.這里V的單位是L，k的單位為atm/L,T的單位為K.

根據圖3所示的三維空間圖，可在整體上把握溫度隨著斜率和體積的變化趨勢.

(1)沿著k軸的正方向，隨著斜率的增大，溫度隨著體積的變化先是呈明顯的倒U形，然后經歷了從倒U形向正U形的過渡，最后呈現明顯的U形.

(2)隨著氣體的范德瓦耳斯系數a,b的增大，三維空間圖上出現了明顯的斷痕，也就是說直線的斜率固定時，對于a,b較大的氣體不可能同時存在多個溫度的轉換點，與表2中所得到的結論相同.并且對于表2中的 a,b系數，a對溫度轉換點起決定作用.

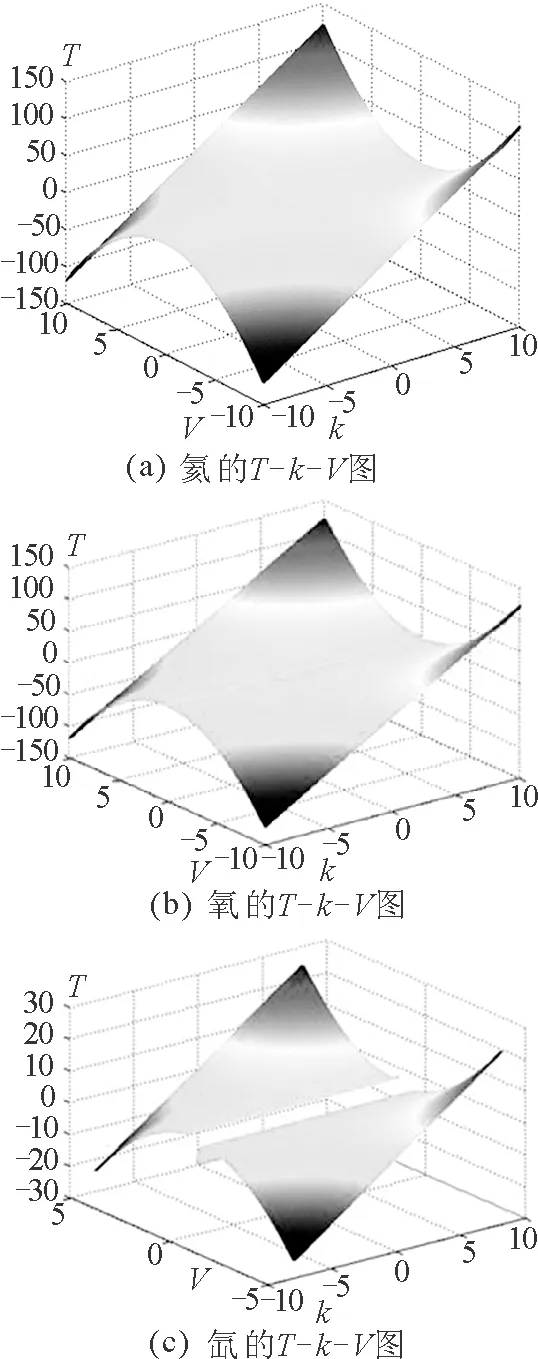
圖3 溫度隨斜率、體積變化趨勢三維空間圖

氣體從M到B的過程中，仍然對外界做功，但是氣體的溫度卻是在降低，顯然，在M到B的過程中既有放熱區，也有吸熱的區，其中必然存在一個從吸熱轉為放熱的過渡點N.

3 N點的狀態參量

1mol的范德瓦耳斯氣體仍然沿直線過程變化，直線的方程為p=k1V+b1，其中k1<0,b1>0.在任意的準靜態過程中，范德瓦耳斯氣體的內能都滿足熱力學第一定律即

dQ=dU+pdV[9]

(7)

3.1 研究范德瓦耳斯氣體的內能表達式

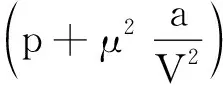
(8)

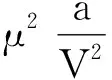
dEk=μCV,mdT

(9)

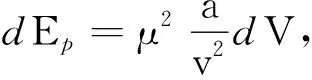
(10)

代入dQ=dU+pdV[9]中可以得

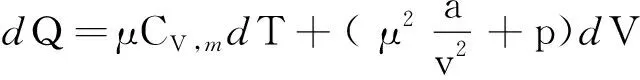
(11)

由1mol范德瓦耳斯氣體的狀態方程和p=k1V+b1，其中k1<0,b1>0，可得

dQ =[(2R-1CV,mk1+k1)V+(R-1CV,mb1-

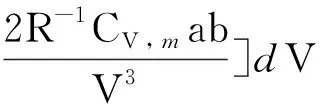
(12)

在吸放熱轉變點滿足dQ=0，當dV>0時，

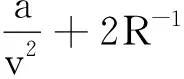
(2R-1CV，mk1+k1)V+(R-1CV,mb1-

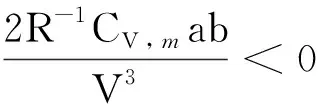
則該區域為放熱區.

對于

可以方程兩邊同時乘以V3，得

(2CV，mk1+k1R)V4+(Rb1+CV,mb1-CV,mk1b)V3+(Ra-CV,ma)V+2CV,mab=0

(13)

對于上面的方程,如果已經知道直線的斜率、截距和氣體的種類，利用Matlab的求根函數roots，即可求出該氣體沿著這條直線變化時熱量轉變點.

3.2 求解氣體在該直線過程中的吸放熱轉換點

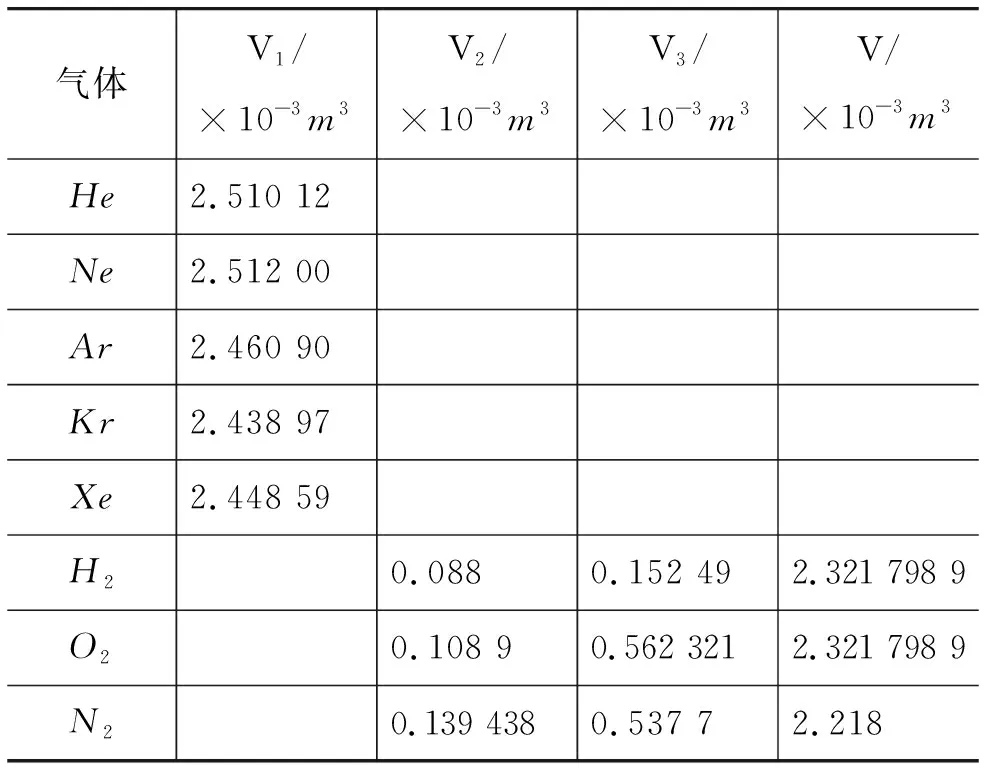
假設n=1mol的氣體也沿著如圖2所示的直線過程變化，其中A為起始狀態，B為終止態.分別求出各個氣體沿著直線變化時熱量的轉變點N的體積(見表3).

表3熱量轉換點N的體積(氣體沿直線變化時)

氣體V1/×10-3m3V2/×10-3m3V3/×10-3m3V/×10-3m3He2.510 12Ne2.512 00Ar2.460 90Kr2.438 97Xe2.448 59H20.0880.152 492.321 798 9O20.108 90.562 3212.321 798 9N20.139 4380.537 72.218

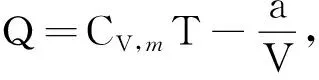
3.4 熱量隨著斜率與體積的變化

若取氣體的直線變化方程為p-p0= k(V-V0) ,其中(p0,V0)是起點，k是直線的斜率.結合1mol范德瓦耳斯氣體的狀態方程和熱力學第一定律Q=U+W[8],可以得到熱量關于斜率和體積的表達式

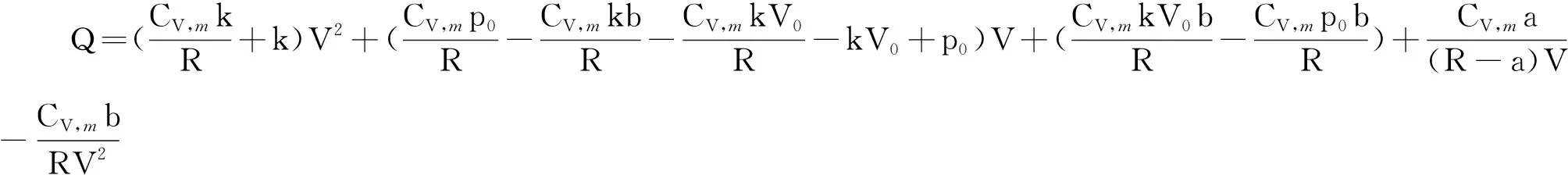
(14)

由式(14)可以看出對于同種氣體,熱量僅僅由k和V確定，如果取原點作為直線的起點，則可以利用Matlab繪出關于熱量、斜率和體積(T,k,V)的三維空間圖如圖4所示.

圖4中橫軸表示k，縱軸表示V，豎軸表示Q,這里V的單位是L，k的單位為atm/L,Q的單位為1.013*102J.

根據圖4的熱量、體積、斜率的關系，可以整體上把握氣體的熱量隨著斜率和體積的變化趨勢.

(1) 對于單原子氣體He和Ne的三維空間圖，熱量隨著斜率和體積的變化趨勢幾乎完全相同，對應的熱量值也相同，而雙原子氣體O2和N2的三維空間圖也幾乎完全相同，這與表3中所得到的結論相同.

(2)隨著斜率的增大，吸熱量Q隨著體積的變化趨勢先是呈明顯的倒U形，然后經歷了從倒U形到正U形的過渡，最后，呈現明顯的U形.這與理想氣體的熱量和斜率體積的變化關系類似.對于理想氣體，斜率數值較大而為負值時，此區域是放熱區，對應于三維空間圖上的倒U形；斜率為正值時為吸熱區，此時對應于三維空間圖上的正U形，從倒U形向正U形的過渡則對應于先吸熱后放熱的區域[4].結合范德瓦耳斯氣體的三維空間圖，不難得到理想氣體的規律對于范德瓦耳斯氣體也成立.

(3)斜率和氣體體積變化量相同時，雙原子氣體的熱量變化值明顯大于單原子，這與表3中所得到的結論一致，這是因為Q由CV,m決定，雙原子氣體的定體摩爾熱容大于單原子.

圖4 熱量、斜率和體積的三維空間圖

4 結論

范氏氣體在同一直線的變化過程中氣體的溫度轉換點主要由氣體的范氏系數a決定，對于a比較大的氣體，其所對應的溫度轉換點的體積也會越大，溫度轉換點的數量最多只有一個.根據溫度與斜率和體積的三維空間圖可知，沿著斜率增加的方向，溫度T隨著體積的變化趨勢呈明顯的U字形.隨著斜率的增大，溫度隨著體積的變化先是呈明顯的倒U形，然后經歷了從倒U形向正U形的過渡，最后呈現明顯的正U形.而范氏氣體在同一直線的變化過程中氣體的熱量轉換點僅僅由氣體的定體摩爾熱容CV,m決定，范氏系數a,b卻不起作用.這一點也可以在熱量、斜率、體積的三維空間圖得到驗證，雙原子氣體間的三維空間圖幾乎完全相同，單原子氣體間也是一樣.并且可以得到對于定體摩爾熱容較大的雙原子氣體，體積變化相同，其對應的熱量變化量大于單原子氣體.熱量對體積和斜率的依賴關系圖還顯示出隨著斜率的變化，吸收熱量Q隨著體積V的變化趨勢也具有明顯的U字形，隨著斜率的增大，熱量Q隨著體積的變化先呈明顯的倒U形，然后經歷從倒U形向正U形的過渡，最后呈現明顯的正U形.倒U形對應于氣體的放熱區域，正U形對應于氣體的吸熱區域，而從倒U形向正U形的過渡對應于先吸熱后放熱的區域，這與理想氣體結論一致.

參考文獻

1 伍文宜.理想氣體直線過程的討論.大學物理，1996,15(07):47～48

2 伍文宜.理想氣體直線過程的再討論.大學物理，1998,2(17):17

3 賈予東.對理想氣體直線過程的再討論.大學物理，1998，17(09)：44～45

4 楊婷婷，騰保華.淺析理想氣體直線過程的吸放熱.物理通報，2011(04)：14～15

5 李向民.關于范德瓦耳斯氣體的若干討論.聊城大學學報(自然科學版)，2003,16(03)：25～26

6D.Halliday&R.Resnick.PartI.NewYork:JohnWiley&Sons,Inc,1977.42～50

7 付清榮，趙建東，張國梁.范德瓦耳斯氣體在任意準靜態過程中吸放熱轉變點的求解方法分析.伊犁師范學院學報(自然科學報)2011，9(03)：23～24

8 馬文蔚.物理學.北京：高等教育出版社，1999.259～262

9 秦允豪.熱學.第二版.北京：高等教育出版社，2004.86～87