返璞歸真 自然和諧

☉江蘇省海安縣曲塘中學(xué)附屬初中 王 軍

返璞歸真 自然和諧

☉江蘇省海安縣曲塘中學(xué)附屬初中 王 軍

解幾何題難，難在作輔助線．輔助線的類型總體上分為直線形和圓兩種，而在平時(shí)數(shù)學(xué)教學(xué)中，對(duì)輔助線的“重直輕曲”現(xiàn)象一直存在.例如文1便出現(xiàn)了避直就迂的現(xiàn)象——舍棄較為簡(jiǎn)捷的作輔助圓的方法，大用特用較為煩瑣的作直線形輔助線解題.文1還指出“構(gòu)造圓是一種巧法，……應(yīng)該選用其他較為簡(jiǎn)潔的通法”，筆者對(duì)此實(shí)在不敢茍同.其實(shí)，作輔助圓不是一種巧法，而是一種重要的通法、求解的方式；對(duì)于同一問題，若同時(shí)能用直線形和圓兩種不同的輔助線方法求解，往往用圓的求解方法更簡(jiǎn)潔、更自然.現(xiàn)從近年中考題中選取兩例，對(duì)它們進(jìn)行幾種不同的方法求解，讓我們共同關(guān)注作輔助圓解題.

例1 （呼和浩特市中考）如圖1，四邊形ABCD中，

點(diǎn)評(píng)：解法1根據(jù)已知條件AB=AD，把題設(shè)已有圖形看成直角三角形的一部分，其中將BD看成直角邊，AD當(dāng)成斜邊上的中線，這樣用補(bǔ)形法作出相等線段構(gòu)成直角三角形，再運(yùn)用直角三角形、等腰三角形、等腰梯形的性質(zhì)進(jìn)行解答.解法2通過作垂線把BD看成直角三角形的斜邊，再解決兩直角邊的長(zhǎng)，又運(yùn)用矩形、等腰三角形的判定和性質(zhì)解題.解法3運(yùn)用截長(zhǎng)法在線段CD上截取DE=AB，使之出現(xiàn)菱形，再利用菱形、等腰梯形的性質(zhì)解答.前三種方法都是作直線形輔助線，用直角三角形、矩形或菱形等直線幾何圖形的判定、性質(zhì)解題，體現(xiàn)出較為煩瑣的解題過程，雖為通法求解，但思維含量大，學(xué)生不易想到.解法4根據(jù)題中已知條件：三條線段相等，且它們有公共端點(diǎn)，學(xué)生容易聯(lián)想到圓的集合定義，作出以共同端點(diǎn)為圓心，以等線段長(zhǎng)為半徑的圓，再用圓的有關(guān)性質(zhì)解題，顯得格外自然而簡(jiǎn)捷，讓人耳目一新.

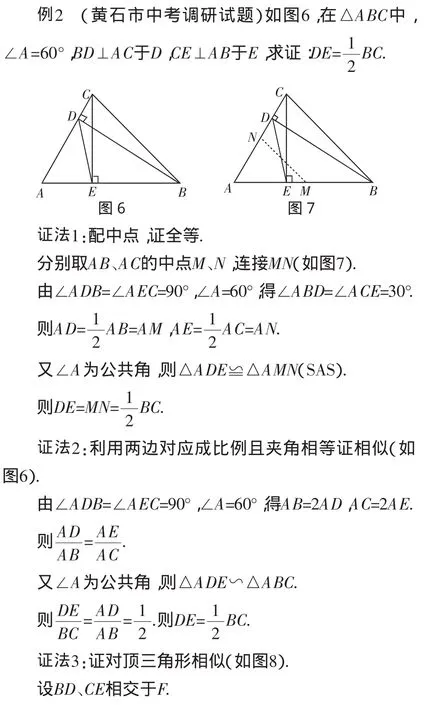
點(diǎn)評(píng)：由結(jié)論的形式易想到要構(gòu)造三角形的中位線，但要證明這兩條線段（線段MN、DE）相等卻比較難．解法1正是遵循這樣的思路，充分利用含60°角的直角三角形的邊的關(guān)系，得到兩對(duì)相等線段AD=AM、AE=AN，再利用三角形全等實(shí)現(xiàn)證題．解法2利用兩個(gè)含60°角的直角三角形，得出短直角邊與斜邊之比為1∶2，從而出現(xiàn)比例式，再利用“兩邊對(duì)應(yīng)成比例且夾角相等”證三角形相似，進(jìn)一步運(yùn)用相似的性質(zhì)證題．解法3通過觀察題設(shè)圖形，發(fā)現(xiàn)其中隱含有兩對(duì)對(duì)頂三角形△CDF和△BEF、△DEF與△CDF，利用前者（兩個(gè)含30°角的直角三角形）的直角邊與斜邊的關(guān)系，得出后面的一對(duì)對(duì)頂三角形相似，并運(yùn)用相似的性質(zhì)進(jìn)行證題．前三種證法雖然都是運(yùn)用直線形知識(shí)進(jìn)行的通法求解，但解答此題對(duì)考生的識(shí)圖、辨圖能力要求較高．上面的證法看似精煉、簡(jiǎn)潔，但解題思維過程的長(zhǎng)度被隱藏，其難度是我們老師無(wú)法想象的．實(shí)際上在考試中，鮮有學(xué)生能用前三種方法來(lái)證題．其實(shí)，也有不少考生采用作輔助圓的方法來(lái)解決問題．這是因?yàn)轭}目的已知條件和圖形已具備作輔助圓的鮮明特征：△BDC和△BCE都是直角三角形，且它們有公共邊BC，取BC的中點(diǎn)后，用圓的定義構(gòu)造以BC為直徑的圓，再綜合運(yùn)用圓的有關(guān)性質(zhì)，則問題易于解決．

從上面兩例可以看出：根據(jù)已知條件，添加適當(dāng)?shù)妮o助圓，可使分散的條件集中，隱蔽的條件明顯，為溝通條件與結(jié)論之間的內(nèi)在聯(lián)系而起到事半功倍的作用．相比其他三種直線形解法，作輔助圓解題較為貼近學(xué)生的認(rèn)知水平，也接近學(xué)生的“最近發(fā)展區(qū)”，符合學(xué)生通常的思維習(xí)慣，有利于學(xué)生的理解和接受，有利于培養(yǎng)和發(fā)展學(xué)生的思維能力、創(chuàng)新意識(shí)．因此作輔助圓是數(shù)學(xué)解題中一種不可缺少、不可忽視的通用的思維方法．平時(shí)教學(xué)中，對(duì)于可作輔助圓的一類問題應(yīng)作詳細(xì)分析、重點(diǎn)講解，應(yīng)展示解題的思維過程，讓學(xué)生知道為什么能夠作出輔助圓，作出輔助圓的目的，之后又怎樣去運(yùn)用圓的性質(zhì)解答等，這樣能使學(xué)生體會(huì)到作輔助圓的由來(lái)和用圓的知識(shí)解題的簡(jiǎn)捷性；進(jìn)行例題講解后，還應(yīng)該及時(shí)補(bǔ)充一定量的相關(guān)習(xí)題，進(jìn)行專題訓(xùn)練，這樣學(xué)生就會(huì)熟練掌握，融會(huì)貫通、熟能生巧，進(jìn)而把輔助圓作為一種必不可少的解題工具、思維方法，自覺運(yùn)用到解題中去．

不少幾何問題明明可用作輔助圓的方法解決，學(xué)生為什么棄之不用呢？經(jīng)筆者調(diào)查、分析和思考，主要原因有以下幾種.

（1）學(xué)生對(duì)圓的內(nèi)容掌握不扎實(shí)，不習(xí)慣把圓作為解決問題的工具．

我們知道，圓是平面幾何中的基本圖形，也是除直線圖形之外的另一特殊曲線圖形；《圓》是初中數(shù)學(xué)極其重要的章節(jié)，在平面幾何中舉足重輕，它比較系統(tǒng)的研究了圓的概念、性質(zhì)、圓中有關(guān)的角、點(diǎn)與圓、直線與圓、圓與圓、圓與正多邊形之間的位置、數(shù)量關(guān)系．雖然現(xiàn)行教材對(duì)圓的內(nèi)容作了大幅度刪減，比如：弦切角、相交弦、切割線、四點(diǎn)共圓等，但圓的基本知識(shí)、結(jié)構(gòu)、框架還在，相比其他章節(jié)，其知識(shí)點(diǎn)仍然龐雜，性質(zhì)定理繁多，運(yùn)用靈活．特別是圓與三角形、四邊形、多邊形、全等、相似、幾何變換、函數(shù)圖像相結(jié)合后，綜合性強(qiáng)，難度大，學(xué)生難以在短時(shí)間內(nèi)學(xué)好．

另外，《圓》一章被安排在九年級(jí)上冊(cè)，在《相似》、《二次函數(shù)》之前，講授《圓》時(shí)，由于受內(nèi)容限制，大都只按部就班，學(xué)完課本的知識(shí)點(diǎn)，便草草了事；而與其他知識(shí)點(diǎn)相關(guān)聯(lián)的內(nèi)容（特別是與相似）都沒有納入教學(xué)之中，而圓與相似相結(jié)合是初中數(shù)學(xué)最為華麗的篇章．這樣，對(duì)《圓》的學(xué)習(xí)僅僅停留在淺層次的運(yùn)用上，對(duì)圓的深層次的運(yùn)用幾乎為空白．最終導(dǎo)致不少學(xué)生對(duì)圓的內(nèi)容較陌生，甚至談“圓”色變．

（2）缺少對(duì)圓輔助線的歸納和總結(jié)．

現(xiàn)行教材雖經(jīng)專家精心設(shè)計(jì)，但在平時(shí)教學(xué)中，我們?nèi)圆荒苷毡拘疲鴳?yīng)不斷加強(qiáng)相關(guān)內(nèi)容的總結(jié)、反思和拓展．學(xué)習(xí)《圓》的內(nèi)容時(shí)，應(yīng)適時(shí)補(bǔ)充與圓有關(guān)的一些重要定理、性質(zhì)，并進(jìn)行運(yùn)用，啟發(fā)、引導(dǎo)學(xué)生對(duì)圓的內(nèi)容的深入探討和細(xì)致研究，這樣便能充分挖掘教材潛在的教學(xué)功能，使學(xué)生的數(shù)學(xué)思維和創(chuàng)新能力得到進(jìn)一步的培養(yǎng)和提高．

平時(shí)教學(xué)中，讓學(xué)生體會(huì)到圓是平面幾何的重要圖形，它不僅能反映圖形中諸多角的關(guān)系，也能建立很多線段間的關(guān)系．應(yīng)引導(dǎo)學(xué)生歸納、總結(jié)圓的基本運(yùn)用、輔助線的作法．構(gòu)造輔助圓的基本思路是：根據(jù)圓的定義添補(bǔ)輔助圓、根據(jù)“圓周角的性質(zhì)”作輔助圓、根據(jù)圓內(nèi)（外）角與圓周角的關(guān)系作輔助圓、根據(jù)“任何三角形都有一個(gè)外接圓”作輔助圓、根據(jù)點(diǎn)與圓的位置關(guān)系作輔助圓、根據(jù)直線與圓的交點(diǎn)個(gè)數(shù)作輔助圓、根據(jù)圓與圓的交點(diǎn)個(gè)數(shù)作輔助圓等，解題時(shí)應(yīng)因題而異，靈活處理．

（3）對(duì)作輔助圓的作用認(rèn)識(shí)不夠．

圓是平面幾何中的重要內(nèi)容，對(duì)培養(yǎng)學(xué)生的識(shí)圖能力、空間轉(zhuǎn)換能力、邏輯推理能力有著重要作用．在中考數(shù)學(xué)試卷中，不光體現(xiàn)在基礎(chǔ)知識(shí)的檢測(cè)上，也體現(xiàn)在綜合解題能力上．例如：由圓和直線圖形、函數(shù)圖像可以組合成一些復(fù)雜的綜合題，由圓的一些性質(zhì)和平面直角坐標(biāo)系、函數(shù)、方程、面積等知識(shí)就組成了涉及面廣、圖形變化大、綜合性強(qiáng)的中考?jí)狠S題．解答它們，往往需要有較強(qiáng)的分析問題、解決問題的能力．

學(xué)生在初學(xué)圓時(shí)，對(duì)一些題目往往感覺無(wú)從下手，這時(shí)如果能夠添加適當(dāng)?shù)妮o助線，問題就簡(jiǎn)單多了．作輔助圓求解幾何問題，能化繁為簡(jiǎn)、化難為易，彰顯了獨(dú)特的解題魅力，它滲透了一些基本的數(shù)學(xué)思想方法，能拓展思路、開闊視野，甚至也會(huì)在問題解決過程中有易如反掌、勢(shì)如破竹的快樂體驗(yàn)，真可謂“直線誠(chéng)可貴，曲線價(jià)更高”．在教學(xué)過程中，既要重視作直線型輔助線的解法，也要重視作輔助圓的解法，以培養(yǎng)學(xué)生敏銳的觀察、深刻的思維與探究能力，提高數(shù)學(xué)素養(yǎng)，獲得終生發(fā)展所必需的數(shù)學(xué)思想方法．

當(dāng)然，筆者強(qiáng)調(diào)作輔助圓解題，絕無(wú)“貶直揚(yáng)曲”的傾向，只是想找回它在教學(xué)中應(yīng)有的位置，兩種不同類型的輔助線解題方法不可或缺，孤立任何一種都不可取．在教學(xué)中，取長(zhǎng)補(bǔ)短，整合優(yōu)化，發(fā)揮各自優(yōu)勢(shì)，這樣學(xué)生的思維和答題，便可以返璞歸真，自然和諧．

1.湯獻(xiàn)玉.立足教材，活用定義［J］.中學(xué)數(shù)學(xué)（下），2011（8）.

2.羅峻.找出隱藏的圓，巧解中考試題［J］.中學(xué)數(shù)學(xué)（下），2011（1）.WG