關注“直L型”圖形模型 重視通法的解題功能

☉寧夏回族自治區中衛市沙坡頭區宣和鎮張洪學校 張 寧

一、基本模型的提煉

例1（2009年深圳）如圖1，矩形ABCD中，由8個面積均為1的小正方形組成L型模板按圖1所示放置，則矩形ABCD的周長為______.

圖1

解析：易知小正方形的邊長為1，所以AE=EF=4，FG=2.

因為∠AEF=90°，所以∠AEB+∠FEC=90°.由∠ABE=90°，得∠BAE+∠AEB=90°.所以∠FEC=∠BAE.又因為∠ABE=∠FCE=90°，AE=EF=4，所以△ABE≌△ECF，所以BE=CF，AB=EC.

令DF=x，則EC=2x，AB=2x.所以FC=DC-DF=2x-x=x，所以BE=x.

點評：本題雖然是一道填空題，但它所涉及的知識點比較多，主要考查全等三角形的判定與性質、相似三角形的判定與性質、矩形的性質、勾股定理等知識點．本題以矩形和直角三角形為背景，構思巧妙，設計新穎，具有較強的探索性，全面考查了學生綜合運用所學知識分析問題和解決問題的能力．它的解法具有廣泛的代表性，是解決同類問題的通法．

近幾年各地中考試題中經常出現以圖1為模型命制的中考試題，由于它的形狀類似于字母“L”，不妨稱這種基本圖形為“直L型”圖形，它是中考命題中一個重要的數學模型，這種模型的通性通法對解決同類問題具有一定的導向作用，在教學中非常有必要引導學生關注“直L型”圖形模型，使學生重視通法的解題功能，本文以近兩年各地中考試題為例，說明“直L型”圖形模型的通法在解題中的應用.

二、“直L型”圖形的性質

1.直角梯形中的“直L型”圖形的性質

如圖2，直角梯形ABCD中，AB∥CD，∠BCD=90°，AB=a，CD=b，BC=c. 若在BC上存在直角點M，使AM⊥DM，則：

圖2

證明：設BM=x，則MC=c-x.

由AM⊥DM，知∠AMD=90°，所以∠AMB+∠DMC=90°.

因為∠ABM=90°，所以∠BAM+∠AMB=90°.

所以∠DMC=∠BAM.

又因為∠ABM=∠DCM=90°，所以△ABM∽△MCD.

所以x2-cx+ab=0.

2.矩形中的“直L型”圖形的性質

如圖3，在矩形ABCD中，AD=a，AB=b，點M在BC邊上，連接AM、DM，∠AMD=90°，點M為直角點.則：

①△ABM∽△MCD；②a≥2b.

證明：設BM=x，則MC=a-x.

圖3

因為∠AMD=90°，所以∠AMB+∠DMC=90°.

因為∠ABM=90°，所以∠BAM+∠AMB=90°.

所以x2-ax+b2=0.由Δ=a2-4b2≥0，知a≥2b.即當BC上存在點直角點M，使AM⊥DM時，a≥2b.反之易知：若a≥2b，則BC上存在直角點M，使AM⊥DM.

以上得出的“直L型”圖形的性質及性質的證明方法在解決同類問題中有著廣泛的應用.

三、“直L型”圖形模型在解中考題中的應用

例2（2012年浙江省嘉興市）在平面直角坐標系xOy中，點P是拋物線y=x2上的動點（點P在笫一象限內）.連接OP，過點O作OP的垂線交拋物線于另一點Q.連接PQ，交y軸于點M.作PA⊥x軸于點A，QB⊥x軸于點B.設點P的橫坐標為m.

①求線段OP的長和tan∠POM的值；

②在y軸上找一點C，使△OCQ是以OQ為腰的等腰三角形，求點C的坐標.

（2）如圖5，連接AM、BM，分別與OP、OQ相交于點D、E.

①用含m的代數式表示點Q的坐標；②求證：四邊形ODME是矩形.

圖4

圖5

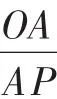
因為PA⊥x軸，所以PA∥MO.

②設Q（n，n2）.

因為tan∠QOB=tan∠POA，

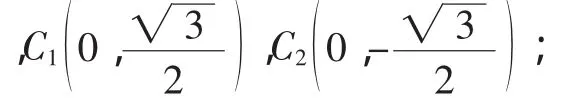
當OQ=CQ時，C3（0，1）.

（2）①P（m，m2），設Q（n，n2）.

②設直線PQ的解析式為y=kx+b.

解得b=1.

所以M（0，1）.

所以∠MAO=∠QOB.

所以QO∥MA.

同理，可得EM∥OD.

所以四邊形ODME是平行四邊形.

又因為∠EOD=90°，所以平行四邊形ODME是矩形.

點評：本題是一道幾何代數綜合題，主要考查一次函數、二次函數、勾股定理、相似三角形的性質與判定、矩形的判定及方程思想、分類討論、特殊到一般的數學思想等的綜合應用．解題的關鍵是靈活應用所學知識，求出關鍵點P、Q、M的坐標．本題中的“直L型”圖形是梯形中的“直L型”圖形，在求點Q的坐標時要充分利用“直L型”圖形中證明三角形相似的方法．

例3（2012年四川省南充市）如圖6，矩形ABCD中，AB=2AD，E為AD的中點，EF⊥EC交AB于點F，連接FC.

（1）求證：△AEF∽△DCE；

（2）求tan∠ECF的值.

分析：（1）由“直L型”圖形中證明三角形相似的方法，易證△AEF∽△DCE.

圖6

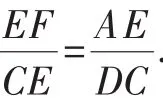
解：（1）在矩形ABCD中，∠A=∠D=90°.

因為EF⊥EC，所以∠FEC=90°.

所以∠FEA+∠CED=90°.

因為∠FEA+∠EFA=90°，所以∠EFA=∠CED.

所以△AEF∽△DCE.

點評：此題考查相似三角形的判定與性質、矩形的性質以及銳角三角函數的定義．此題難度適中，在根據題意無法直接求得三角形的邊長時，可考慮利用三角形的相似關系，利用“直L型”圖形中相似三角形的證法易知△AEF∽△DCE，通過利用“相似三角形對應邊成比例”的性質，結合題中的線段間的倍數關系，推得∠ECF的三角函數值，解題時還要注意數形結合思想的應用．

例4（2011年湖南省衡陽市）如圖7，在矩形ABCD中，AD=4，AB=m（m＞4），點P是AB邊上的任意一點（不與A、B重合），連接PD，過點P作PQ⊥PD，交直線BC于點Q.

（1）當m=10時，是否存在點P，使得點Q與點C重合？若存在，求出此時AP的長；若不存在，說明理由.

（2）連接AC，若PQ∥AC，求線段BQ的長（用含m的代數式表示）.

（3）若△PQD為等腰三角形，求以P、Q、C、D為頂點的四邊形的面積S與m之間的函數關系式，并寫出m的取值范圍.

解：（1）假設當m=10時，存在點P，使得點Q與點C重合，如圖8所示.

因為PQ⊥PD，所以∠DPC=90°.

所以∠APD+∠BPC=90°.

又因為∠ADP+∠APD=90°，所以∠BPC=∠ADP.

又∠B=∠A=90°，所以△PBC∽△DAP.

解得AP=2或8.

故存在點P，使得點Q與點C重合，此時AP的長為2或8.

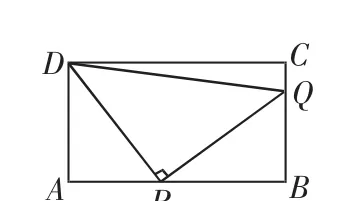
圖7

圖8

圖9

（2）如圖9，因為PQ∥AC，所以∠BPQ=∠BAC.

又因為∠BPQ=∠ADP，所以∠BAC=∠ADP.

又因為∠B=∠DAP=90°，所以△ABC∽△DAP.

由∠BPQ=∠BAC，∠B=∠B，得△PBQ∽△ABC.

（3）由于已知PQ⊥PD，所以只有當DP=PQ時，△PQD為等腰三角形.

由∠BPQ=∠ADP，∠B=∠A=90°，DP=PQ，得△PBQ≌△DAP.

所以PB=DA=4，AP=BQ=m-4.

故以P、Q、C、D為頂點的四邊形的面積S與m之間的函數關系式為：

點評：本題主要考查相似三角形的判定與性質、全等三角形的判定與性質、一元二次方程的解法.問題（1）是存在型問題，解決這類問題時，首先假設存在點P，使得點Q與點C重合，然后充分利用“直L型”圖形中相似三角形的證明方法說明△PBC∽△DAP，利用相似三角形的性質列出關于三角形某一邊長的一元二次方程，如果方程有解，則存在滿足條件的點；如果方程無解，則不存在滿足條件的點.這種方法也是解決其他類型存在性問題時常用的方法.

例5 （2012年山東泰安）如圖10，E是矩形ABCD的邊BC上一點，EF⊥AE，EF分別交AC、CD于點M、F，BG⊥AC，垂足為G，BG交AE于點H.

圖10

（1）求證：△ABE∽△ECF；

（2）找出與△ABH相似的三角形，并證明；

（3）若E是BC的中點，BC=2AB，AB=2，求EM的長.

分析：（1）由“直L型”圖形中證明三角形相似的方法，易證△ABE∽△ECF.

（2）由BG⊥AC，易證得∠ABH=∠ECM.

又∠BAH=∠CEM，即可證得△ABH∽△ECM.

（3）如圖11，作MR⊥BC，垂足為R.

圖11

解：（1）因為四邊形ABCD是矩形，所以∠ABE=∠ECF=90°.

因為AE⊥EF，所以∠AEB+∠FEC=90°.

又∠BAE+∠AEB=90°，所以∠BAE=∠CEF.

所以△ABE∽△ECF.

（2）△ABH∽△ECM.

因為BG⊥AC，所以∠ABG+∠BAG=90°.

所以∠ABH=∠ECM.

由（1）知∠BAH=∠CEM，所以△ABH∽△ECM.

（3）作MR⊥BC，垂足為R.

點評：本題考查矩形的性質、直角三角形的性質、相似三角形的判定與性質以及三角函數等知識．解題時注意數形結合思想的應用，注意掌握“有兩組角對應相等的兩個三角形相似”定理的應用．問題 （1）中證明△ABE∽△ECF時，要充分利用“直L型”圖形中證明三角形相似的方法，問題（1）也是解決后面問題的關鍵，所以“直L型”圖形中證明三角形相似的方法在解決問題中起到了至關重要的作用，所以在教學中要特別重視通法的解題功能．

從以上中考試題可以看出，“直L型”圖形的性質有著廣泛的應用．它提供的證明三角形相似的方法和解題思路對解決同類問題具有一定的導向作用．如果教師在中考復習教學中設計一節專門探究“直L型”圖形性質的數學活動課，引導學生關注“直L型”圖形模型，通過師生共同探究“直L型”圖形的性質，一定能激發學生學習數學的興趣，讓學生掌握“直L型”問題中證明三角形相似的方法和解題思路，使學生不僅學會解答與“直L型”圖形有關的中考題，引導學生重視通法的解題功能，而且能有效提高學生應用所學數學知識分析問題和解決問題的能力.