軌道基準(zhǔn)網(wǎng)平面測(cè)量及其數(shù)據(jù)處理的探討
王建紅
(中鐵第一勘察設(shè)計(jì)院集團(tuán)有限公司,西安 710043)
1 概述
無砟軌道具有整體穩(wěn)定性強(qiáng)、剛度均勻性好、線路平順度高、耐久性強(qiáng)的突出優(yōu)點(diǎn),并可顯著減少后期線路的維修工作量。而CRTSⅡ型板式無砟軌道作為其中一種重要的無砟軌道結(jié)構(gòu)形式,在高速鐵路建設(shè)中已經(jīng)得到廣泛應(yīng)用,并已在許多方面顯示出明顯的優(yōu)越性,取得了良好的技術(shù)效益和經(jīng)濟(jì)效益[1]。CRTSⅡ型板式無砟軌道與其他無砟軌道結(jié)構(gòu)的重要區(qū)別是多一級(jí)加密控制網(wǎng),這一級(jí)稱為軌道基準(zhǔn)網(wǎng)。其由一系列的軌道基準(zhǔn)點(diǎn)組成,軌道基準(zhǔn)點(diǎn)設(shè)于混凝土底座或支承層上,位于軌道板橫接縫的中央、相應(yīng)里程中心點(diǎn)的法線上,偏離軌道中線0.10 m。曲線地段置于軌道中線內(nèi)側(cè);直線地段置于線路中線同一側(cè)。軌道基準(zhǔn)網(wǎng)是一個(gè)精度極高的三維控制網(wǎng),但實(shí)際測(cè)量中是將平面、高程分開處理,因此,軌道基準(zhǔn)網(wǎng)平面測(cè)量是軌道基準(zhǔn)網(wǎng)建網(wǎng)測(cè)量的一個(gè)重要組成部分,其相鄰軌道基準(zhǔn)點(diǎn)之間的相對(duì)點(diǎn)位中誤差≤0.2 mm,測(cè)量精度滿足下列要求[2]:
(1)軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差≤0.4 mm;
(2)重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)的平面位置允許偏差:橫向≤0.3 mm,縱向≤0.4 mm。
軌道基準(zhǔn)網(wǎng)作為一種從德國(guó)引進(jìn)的全新的建網(wǎng)方法,其測(cè)量和數(shù)據(jù)處理方法以及精度控制指標(biāo)跟我國(guó)常規(guī)的測(cè)量方法有很多不同之處,因此有必要對(duì)軌道基準(zhǔn)網(wǎng)平面測(cè)量及其數(shù)據(jù)處理進(jìn)行詳細(xì)的探討。
2 軌道基準(zhǔn)網(wǎng)平面測(cè)量
軌道基準(zhǔn)網(wǎng)平面測(cè)量在軌道板粗鋪之前配合專門的不等長(zhǎng)三腳支架分左、右線分別進(jìn)行,具體可概括為半測(cè)回、多次重復(fù)測(cè)量、單向(后退)、搭接。如圖1所示,以右線軌道基準(zhǔn)網(wǎng)平面測(cè)量為例,介紹軌道基準(zhǔn)網(wǎng)平面測(cè)量的具體實(shí)施過程。
(1)測(cè)站點(diǎn)架設(shè)在軌道基準(zhǔn)點(diǎn)的連線方向上,以便優(yōu)先利用全站儀的測(cè)角高精度性,并離最近的軌道基準(zhǔn)點(diǎn)的距離不小于6.5 m,且所有觀測(cè)的軌道基準(zhǔn)點(diǎn)在測(cè)站的同一側(cè)。
(2)直接測(cè)量測(cè)站點(diǎn)附近的4對(duì)CPⅢ點(diǎn)和軌道基準(zhǔn)點(diǎn)的坐標(biāo),軌道基準(zhǔn)點(diǎn)測(cè)量個(gè)數(shù)從11~14個(gè)不等。
(3)測(cè)站上的CPⅢ控制點(diǎn)和軌道基準(zhǔn)點(diǎn)平面測(cè)量觀測(cè)順序如下:
①順時(shí)針觀測(cè)測(cè)站前后共計(jì)4對(duì)CPⅢ點(diǎn);
②由遠(yuǎn)及近按順序觀測(cè)軌道基準(zhǔn)點(diǎn);
③與步驟①一樣再次半測(cè)回觀測(cè)相同的4對(duì)CPⅢ點(diǎn);
④再次由遠(yuǎn)及近按順序觀測(cè)軌道基準(zhǔn)點(diǎn);
⑤與步驟①一樣再次半測(cè)回觀測(cè)相同的4對(duì)CPⅢ點(diǎn);
⑥再次由遠(yuǎn)及近順序觀測(cè)軌道基準(zhǔn)點(diǎn);
⑦與步驟①一樣再次半測(cè)回觀測(cè)相同的4對(duì)CPⅢ點(diǎn)。
(4)對(duì)CPⅢ和軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差進(jìn)行檢查,對(duì)于超限的數(shù)據(jù)及時(shí)重測(cè)。
(5)更換測(cè)站后,相鄰測(cè)站重疊觀測(cè)CPⅢ控制點(diǎn)不少于2對(duì)、軌道基準(zhǔn)點(diǎn)5個(gè)。
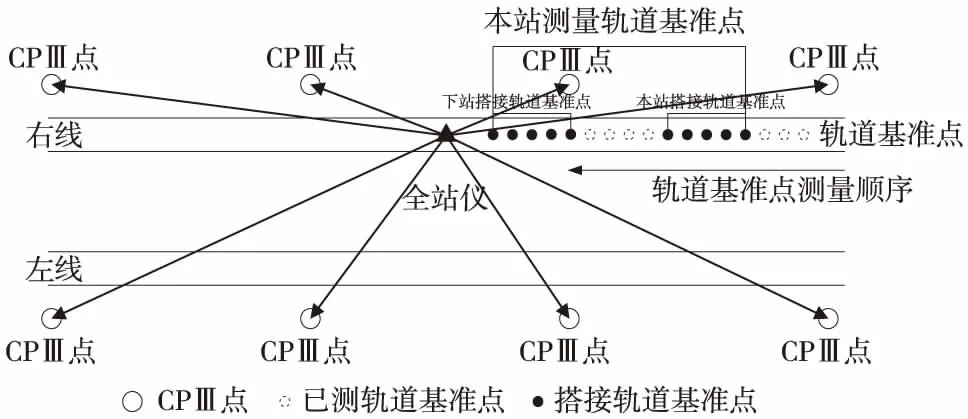
圖1 軌道基準(zhǔn)網(wǎng)平面測(cè)量示意(右線)
3 軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)處理
軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)處理的基本流程是:先進(jìn)行測(cè)站內(nèi)數(shù)據(jù)處理,測(cè)站內(nèi)處理合格后,再進(jìn)行相鄰測(cè)站間的平順搭接處理,下面對(duì)軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)處理基本流程的每一個(gè)環(huán)節(jié)進(jìn)行詳細(xì)的探討。
3.1 外業(yè)觀測(cè)數(shù)據(jù)質(zhì)量檢查
對(duì)外業(yè)采集到的CPⅢ和軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其均值間的較差進(jìn)行質(zhì)量檢查,文獻(xiàn)[2]中只給出“軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差≤0.4 mm”的要求,對(duì)CPⅢ點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其均值間的較差并未作明確的要求,但可以從“軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差≤0.4 mm”的要求出發(fā),推導(dǎo)CPⅢ點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差,具體推導(dǎo)過程如下所述。
由“軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差≤0.4 mm”的要求可知,對(duì)于x坐標(biāo),軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差極限情況其中的一種為
x1-x1+x2+x33=0.4 mm
x2-x1+x2+x33=-0.4 mm
x3-x1+x2+x33=0.0 mm(1)
對(duì)式(1)中的前兩式進(jìn)行簡(jiǎn)單運(yùn)算后,有
(x1-x2)+(x1-x3)=1.2 mm
(x1-x2)+(x3-x2)=1.2 mm(2)
由式(2)可知,當(dāng)且僅當(dāng)(x1-x2)=(x1-x3)=(x3-x2)=0.6 mm時(shí),式(2)中的兩式均取得最大值。
由于CPⅢ點(diǎn)觀測(cè)的測(cè)回?cái)?shù)是4個(gè)測(cè)回,因此對(duì)照式(1)和式(2),對(duì)于CPⅢ點(diǎn)的x坐標(biāo),CPⅢ點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差的限差Δx限可寫作
Δx限=(x1-x2)+(x1-x3)+(x1-x4)4(3)
由式(3)可知,當(dāng)且僅當(dāng)(x1-x2)=(x1-x3)=(x1-x4)時(shí),式(3)取得最大值。并將(x1-x2) mm帶入式(3),得到Δx限=0.45 mm。亦即:CPⅢ點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差≤0.45 mm。
因此可以看出,CPⅢ和軌道基準(zhǔn)點(diǎn)由于外業(yè)觀測(cè)的測(cè)回?cái)?shù)不同,導(dǎo)致了CPⅢ和軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差也不同,因此,在軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)外業(yè)觀測(cè)質(zhì)量檢查時(shí),應(yīng)對(duì)CPⅢ和軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差設(shè)定不同的限差進(jìn)行檢查。
3.2 站內(nèi)平面坐標(biāo)的轉(zhuǎn)換
在外業(yè)觀測(cè)數(shù)據(jù)質(zhì)量檢查合格后,得到各CPⅢ和軌道基準(zhǔn)點(diǎn)的平均值。由于此時(shí)的CPⅢ和軌道基準(zhǔn)點(diǎn)所在的坐標(biāo)系是任意的測(cè)站坐標(biāo)系,所以需要將其轉(zhuǎn)換到線路坐標(biāo)系,而平面坐標(biāo)系之間轉(zhuǎn)換一般常用的方法有相似變換法[3]和仿射變換法[4],相似變換法又分為三參數(shù)和四參數(shù)兩種轉(zhuǎn)換模型。對(duì)于四參數(shù)相似變換法,亦即[3]
x線路
y線路=x0
y0+(1+k)cosθsinθ
-sinθcosθx任意
y任意(4)
式中x0、y0——平移參數(shù);
k——尺度;
θ——旋轉(zhuǎn)角。
對(duì)于三參數(shù)相似變換法,即在式(4)中不考慮尺度k。
而仿射變換法的模型為[4]
x線路=ax任意+by任意+c
y線路=dx任意+ey任意+f(5)
式中a、e——分別確定點(diǎn)(x任意,y任意)在輸出坐標(biāo)中x線路方向和y線路方向上的縮放尺度;
b、d——確定旋轉(zhuǎn)角度;
c、f——分別確定在x線路方向和y線路方向上的水平平移尺寸。
由于軌道基準(zhǔn)網(wǎng)的測(cè)量和數(shù)據(jù)處理方法是從德國(guó)引進(jìn)的,在國(guó)內(nèi)尚處于研究和起步階段。軌道基準(zhǔn)網(wǎng)站內(nèi)平面坐標(biāo)的轉(zhuǎn)換采用何種坐標(biāo)轉(zhuǎn)換方法無法確定,而德國(guó)軌道基準(zhǔn)網(wǎng)數(shù)據(jù)處理軟件采用的是馬克斯·博格建筑公司的“FFBoegl-PVP construction”軟件(以下簡(jiǎn)稱為“PVP軟件”),因此,為了確定軌道基準(zhǔn)網(wǎng)站內(nèi)平面坐標(biāo)的轉(zhuǎn)換采用的坐標(biāo)轉(zhuǎn)換方法,可以采用上面所述的幾種坐標(biāo)轉(zhuǎn)換方法,對(duì)大量的軌道基準(zhǔn)網(wǎng)測(cè)量數(shù)據(jù)進(jìn)行坐標(biāo)轉(zhuǎn)換,并分別將坐標(biāo)轉(zhuǎn)換結(jié)果與PVP軟件的計(jì)算結(jié)果進(jìn)行比較。由于計(jì)算的數(shù)據(jù)量比較多,下面僅列出其中一站的軌道基準(zhǔn)點(diǎn)坐標(biāo)比較情況,見表1。
從表1可以看出,三參數(shù)相似變換法計(jì)算結(jié)果與PVP軟件計(jì)算結(jié)果沒有任何差異,而四參數(shù)相似變換法和仿射變換法計(jì)算結(jié)果與PVP軟件計(jì)算結(jié)果差異明顯,特別是仿射變換法。這個(gè)結(jié)果是與大量的軌道基準(zhǔn)網(wǎng)測(cè)量數(shù)據(jù)計(jì)算結(jié)果一致的,因此可以確定軌道基準(zhǔn)網(wǎng)站內(nèi)平面坐標(biāo)的轉(zhuǎn)換采用的是三參數(shù)相似變換法。
3.3 站間平面坐標(biāo)的搭接
軌道基準(zhǔn)網(wǎng)測(cè)站內(nèi)處理合格后,接著要進(jìn)行相鄰測(cè)站間的平順搭接處理。通過前面的軌道基準(zhǔn)網(wǎng)平面測(cè)量方法介紹知道,軌道基準(zhǔn)網(wǎng)平面測(cè)量是由多個(gè)測(cè)站組成的,不同測(cè)站由于換站的原因使得相鄰測(cè)站之間重疊觀測(cè)5個(gè)軌道基準(zhǔn)點(diǎn)的測(cè)量坐標(biāo)存在偏差,如果不進(jìn)行平順搭接處理,勢(shì)必會(huì)形成轉(zhuǎn)角或突變。為了解決這個(gè)問題,對(duì)相鄰測(cè)站之間重疊觀測(cè)的5個(gè)軌道基準(zhǔn)點(diǎn)采用余弦曲線加權(quán)平滑的方法進(jìn)行相鄰測(cè)站之間的平順搭接處理。
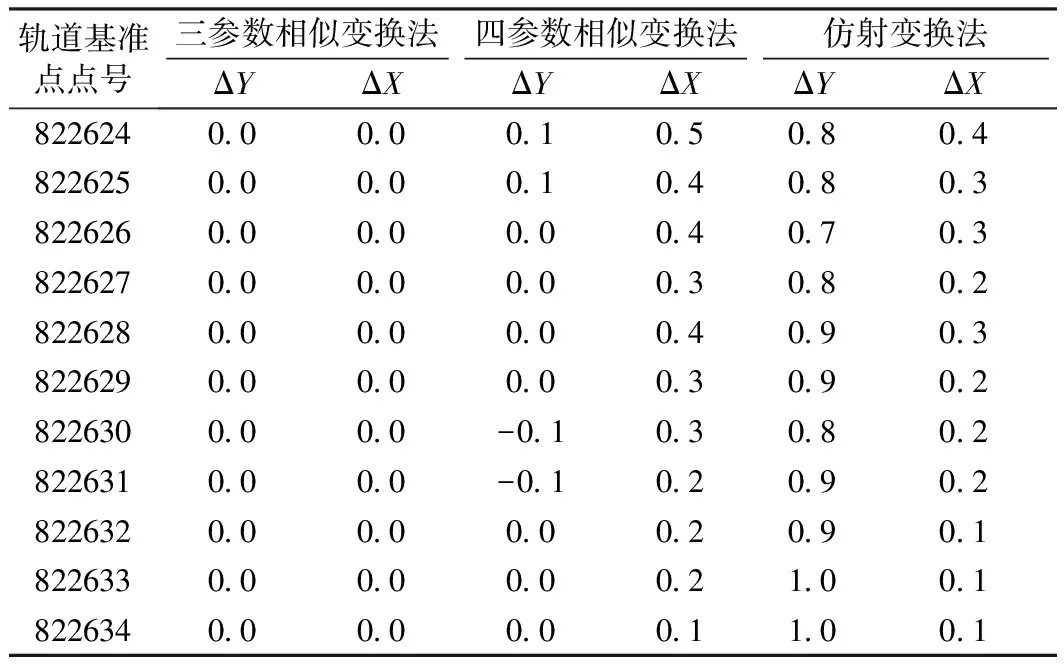
表1 不同坐標(biāo)轉(zhuǎn)換方法計(jì)算結(jié)果與PVP軟件計(jì)算結(jié)果比較 mm
如圖2所示,賦予前一測(cè)站坐標(biāo)的權(quán)為Z,后一測(cè)站坐標(biāo)的權(quán)為1-Z。其中,Z的函數(shù)表達(dá)式為
Z=cos((π/L)×I)/2+0.5(6)
式中L——搭接長(zhǎng)度,重復(fù)點(diǎn)號(hào)前后各延長(zhǎng)1個(gè)點(diǎn),m;
I——當(dāng)前點(diǎn)離重合起始點(diǎn)的距離,m。
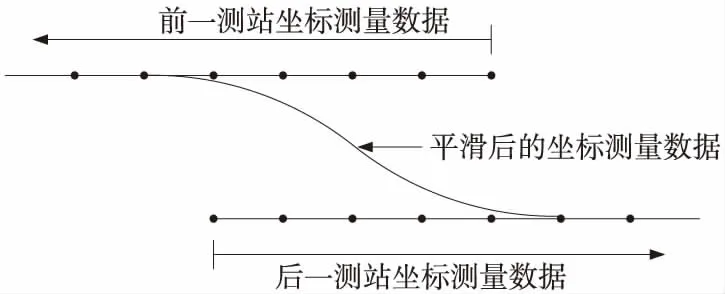
圖2 軌道基準(zhǔn)網(wǎng)平面測(cè)量余弦曲線加權(quán)平滑示意
利用余弦曲線加權(quán)平滑方法得到相鄰測(cè)站重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)的平滑坐標(biāo)之后,根據(jù)文獻(xiàn)[2]的規(guī)定,重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)的平面位置允許偏差:橫向≤0.3 mm,縱向≤0.4 mm。該平面位置允許偏差的定義指的是重疊區(qū)內(nèi)每個(gè)軌道基準(zhǔn)點(diǎn)的橫向、縱向改正量,即重疊區(qū)端部(任意一端)橫向、縱向差值,分配到各軌道基準(zhǔn)點(diǎn)上的改正值。亦即前、后測(cè)站的橫向、縱向坐標(biāo)與平滑后橫向、縱向坐標(biāo)的較差分別應(yīng)≤(0.3×n)mm、≤(0.4×n)mm,其中,n為重疊觀測(cè)的軌道基準(zhǔn)點(diǎn)個(gè)數(shù)。
基于重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)的平面位置偏差的定義,可知,對(duì)于判定相鄰測(cè)站之間搭接是否合格的重要指標(biāo),就是重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)坐標(biāo)分別轉(zhuǎn)換到線路方向的坐標(biāo)系后,其橫向、縱向坐標(biāo)與平滑后橫向、縱向坐標(biāo)的較差的大小,因此將軌道基準(zhǔn)點(diǎn)從線路坐標(biāo)系轉(zhuǎn)換到線路方向坐標(biāo)系成為相鄰測(cè)站之間平順搭接處理的關(guān)鍵環(huán)節(jié)。嚴(yán)密的做法是將軌道基準(zhǔn)點(diǎn)的測(cè)量坐標(biāo)與線路設(shè)計(jì)參數(shù)結(jié)合,計(jì)算重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)處的線路切線方位角,據(jù)此線路切線方位角將重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)坐標(biāo)轉(zhuǎn)換到線路方向。該方法計(jì)算嚴(yán)密,但計(jì)算過程比較繁瑣。考慮到無砟軌道平面曲線半徑都比較大,一般最小為7 000 m[5],因此,能否直接用重疊區(qū)內(nèi)首尾兩個(gè)軌道基準(zhǔn)點(diǎn)坐標(biāo)反算的近似方位角代替重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)處的線路切線方位角用于坐標(biāo)轉(zhuǎn)換值得探討。
如圖3所示,點(diǎn)1~5為相鄰測(cè)站之間重疊觀測(cè)的5個(gè)軌道基準(zhǔn)點(diǎn),并假設(shè)這5個(gè)軌道基準(zhǔn)點(diǎn)的位置都位于半徑為7 000 m的圓曲線上。因此,軌道基準(zhǔn)點(diǎn)1處的線路切線方位角與近似方位角的差值Δα為5個(gè)軌道基準(zhǔn)點(diǎn)處的線路切線方位角與近似方位角差值的最大取值,其值可以按下式計(jì)算
Δα=(90°×l)(π×R)=(90°×4×6.5 m)(π×7 000 m)=0.106°(7)
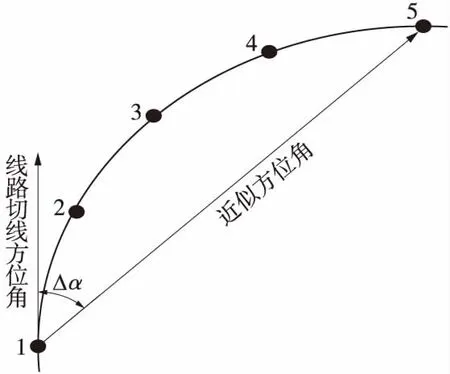
圖3 線路切線方位角與近似方位角關(guān)系示意
若在該點(diǎn)處用重疊區(qū)內(nèi)首尾兩個(gè)軌道基準(zhǔn)點(diǎn)坐標(biāo)反算的近似方位角代替線路切線方位角用于坐標(biāo)轉(zhuǎn)換可行的話,必定也適用于其他任何相鄰測(cè)站之間重疊觀測(cè)的軌道基準(zhǔn)點(diǎn)。下面給出具體的推導(dǎo)過程。
根據(jù)重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)的平面位置偏差的定義,并結(jié)合式(4)和式(6),以及軌道基準(zhǔn)點(diǎn)1的前測(cè)站坐標(biāo)(x1前,y1前)和后測(cè)站坐標(biāo)(x1后,y1后),可寫出該點(diǎn)前站坐標(biāo)轉(zhuǎn)換為橫向、縱向坐標(biāo)與平滑后橫向、縱向坐標(biāo)的較差Δ1前橫、Δ1前縱計(jì)算式為
Δ1前縱=[cosα×x1前+sinα×y1前]-
[0.933×(cosα×x1前+sinα×y1前)+
0.067×(cosα×x1后+sinα×y1后)]
Δ1前橫=[-sinα×x1前+cosα×y1前]-
[0.933×(-sinα×x1前+cosα×y1前)+
0.067×(-sinα×x1后+cosα×y1后)](8)
式中α——軌道基準(zhǔn)點(diǎn)1處的線路切線方位角,以弧度為單位。
對(duì)式(8)進(jìn)行全微分,得
dΔ1前縱=Δ1前橫×dαρ
dΔ1前橫=-Δ1前縱×dαρ(9)
將Δ1前橫=1.5 mm,Δ1前縱=2.0 mm,以及式(7)帶入式(9),可得
dΔ1前縱=0.003 mm
dΔ1前橫=-0.004 mm(10)
上面給出了在軌道基準(zhǔn)點(diǎn)1處用近似方位角代替該點(diǎn)處的線路切線方位角,對(duì)該點(diǎn)前站坐標(biāo)轉(zhuǎn)換為橫向、縱向坐標(biāo)與平滑后橫向、縱向坐標(biāo)的較差的影響情況。對(duì)于該點(diǎn)的后站坐標(biāo)轉(zhuǎn)換為橫向、縱向坐標(biāo)與平滑后橫向、縱向坐標(biāo)的較差的影響情況的推導(dǎo)與上述過程類似,其計(jì)算結(jié)果與式(10)的計(jì)算結(jié)果相同,不再贅述。從式(10)的結(jié)果可以看出:用近似方位角代替該點(diǎn)處的線路切線方位角,對(duì)重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)平面位置偏差的影響甚微,因此,用重疊區(qū)內(nèi)首尾兩個(gè)軌道基準(zhǔn)點(diǎn)坐標(biāo)反算的近似方位角代替重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)處的線路切線方位角,計(jì)算重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)平面位置偏差是可行的。
4 結(jié)語(yǔ)
本文從軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)處理的基本流程入手,對(duì)軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)處理的每一個(gè)環(huán)節(jié)進(jìn)行了詳細(xì)的探討。得到如下結(jié)論:
(1)在軌道基準(zhǔn)網(wǎng)平面數(shù)據(jù)外業(yè)觀測(cè)質(zhì)量檢查時(shí),由于CPⅢ和軌道基準(zhǔn)點(diǎn)外業(yè)觀測(cè)的測(cè)回?cái)?shù)不同,應(yīng)對(duì)CPⅢ和軌道基準(zhǔn)點(diǎn)各半測(cè)回測(cè)量的坐標(biāo)值與其平均值間的較差設(shè)定不同的限差進(jìn)行檢查;
(2)對(duì)大量的軌道基準(zhǔn)網(wǎng)測(cè)量數(shù)據(jù)通過不同的模型進(jìn)行坐標(biāo)轉(zhuǎn)換,并分別將坐標(biāo)轉(zhuǎn)換結(jié)果與PVP軟件的計(jì)算結(jié)果進(jìn)行比較,確定了軌道基準(zhǔn)網(wǎng)站內(nèi)平面坐標(biāo)的轉(zhuǎn)換采用的是三參數(shù)相似變換法;
(3)用重疊區(qū)內(nèi)首尾兩個(gè)軌道基準(zhǔn)點(diǎn)坐標(biāo)反算的近似方位角代替重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)處的線路切線方位角,計(jì)算重疊區(qū)內(nèi)軌道基準(zhǔn)點(diǎn)平面位置偏差是可行的。
[1] 李中華.CRTSⅠ型與CRTSⅡ型板式無砟軌道結(jié)構(gòu)特點(diǎn)分析[J].華東交通大學(xué)學(xué)報(bào),2010,27 (1):22-28.
[2] 中華人民共和國(guó)鐵道部.TB 10601—2009 高速鐵路工程測(cè)量規(guī)范[S].北京:中國(guó)鐵道出版社,2009.
[3] 丁士俊,張忠明.幾種不同坐標(biāo)變換方法問題的研究[J].四川測(cè)繪,2005,28(1):16-19.
[4] 田福娟.平面坐標(biāo)轉(zhuǎn)換軟件設(shè)計(jì)[J].湖北水利水電職業(yè)技術(shù)學(xué)院學(xué)報(bào),2006,2(2):9-14.
[5] 中華人民共和國(guó)鐵道部.TB 10621—2009 高速鐵路設(shè)計(jì)規(guī)范(試行)[S].北京:中國(guó)鐵道出版社,2009.
[6] 陳順寶,任建春,亓月,等.抵償任意帶高斯投影平面坐標(biāo)系選擇的研究[J].測(cè)繪通報(bào),2005(7):21-23.
[7] 韓雪培,廖邦固.地方坐標(biāo)系與國(guó)家坐標(biāo)系轉(zhuǎn)換方法探討[J].測(cè)繪通報(bào),2004(10):20-22.
[8] 武漢大學(xué)測(cè)繪學(xué)院-測(cè)量平差學(xué)科組.誤差理論與測(cè)量平差基礎(chǔ)[M].武漢:武漢大學(xué)出版社,2005.
[9] 於宗儔,于正林.測(cè)量平差原理[M].武漢:武漢測(cè)繪科技大學(xué)出版社,1989.
[10] 程昂,劉成龍,徐小左.CPⅢ平面網(wǎng)必要點(diǎn)位精度的研究[J].鐵道工程學(xué)報(bào),2009,124(1):44-48.
[11] 劉成龍,楊友濤,徐小左.高速鐵路CPⅢ交會(huì)網(wǎng)必要測(cè)量精度的仿真計(jì)算[J].西南交通大學(xué)學(xué)報(bào),2008(6):718-723.
[12] 吳向陽(yáng),魏小寧.關(guān)于GPS網(wǎng)平差中若干特殊問題的處理[J].測(cè)繪通報(bào),2004(7):9-11.

