仿真試驗條件下飛行器外部靜態磁環境模擬

還迎春 林春生 余 杰

（海軍工程大學兵器工程系 武漢 430033）

在進行磁干擾補償模型系數求解時，一般要求飛機首先進行四航向機動學習飛行，用時幾十min，然后將學習樣本數據用于模型系數求解［1］．這種方法不適合在要求快速反應的飛行器上使用．根據飛行器載體磁干擾的產生機理，研究在實驗室條件下對飛行器載體磁干擾補償模型系數精確求解的方法，為飛行器磁干擾補償模型求解提供一種不依賴于機動飛行學習的實用方法，省掉飛行器的學習飛行時間，對保證裝備的快速反應能力有重要意義．本文在實驗室條件下使用仿真方法，生成飛行器的外部靜態地磁環境，作用于飛行器，用安裝于飛行器內部的光泵磁強計和三軸磁通門磁強計同步采集飛行器背景磁場數據，據此求解出飛行器磁干擾補償模型的剩磁和感磁參數．由于該方法可以模擬任意地點的地磁場數據，同時能模擬飛行器在地磁坐標中的任意方向．因此，該方法具有全球適應性，模型穩定性高，樣本數據測量過程無需移動飛行器載體，模型求解速度快、效率高等優點．

1 三軸地磁矢量的模擬方法

根據Tolles－Lawson方程，飛行器背景總干擾磁場可表示成［2－3］

式 中：u1＝

Pi為剩磁參數；aij為感磁參數；bij為渦流磁場參數．

為了求解上式中的模型參數，需要模擬飛行器在地磁場運動時所經歷的外部磁場環境，使飛行器在地磁環境磁化產生飛行器背景干擾磁場的數據樣本，并由式（1）生成關于模型參數的回歸方程組，進而解出模型參數．

首先討論三軸地磁矢量的模擬方法，見圖1，采用三軸正交放置的線圈，通過計算機控制線圈驅動電流來產生三軸磁場矢量［4－5］．由于三軸線圈存在安裝誤差，不是嚴格正交放置，因此產生的磁場矢量的3個分量，不僅與對應線圈的驅動電流有關，而且與其他兩個線圈的驅動電流有關．為了描述磁場矢量與驅動電流的關系，對線圈的放置作如下限制：（1）z′軸線圈沿垂直方向放置，磁場向下為正；（2）x′軸線圈沿南北方向放置，磁場向北為正；（3）y′軸線圈沿東西方向放置，磁場向東為正．

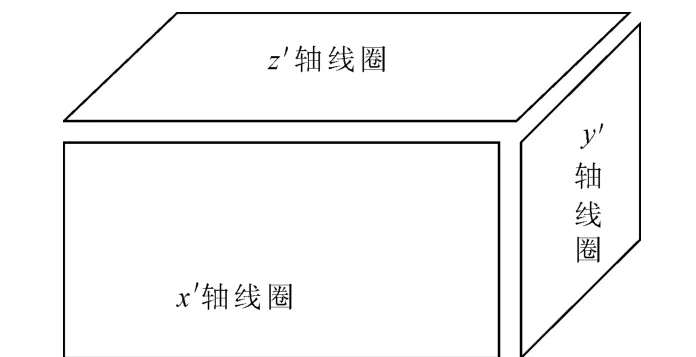
圖1 正交三軸線圈示意圖

由于線圈安置的誤差，線圈軸線x′，y′，z′不能構成正交坐標系，故建立直角坐標系xyz如圖2所示：（1）坐標z軸與z′軸線圈的軸線重合，向下為正；（2）坐標y軸與z′軸線圈和y′軸線圈的軸線共面，y軸向東為正；（3）坐標x軸垂直于y軸和z軸．因而也垂直于y′軸線圈軸線和z′軸線圈軸線，x軸向北為正．

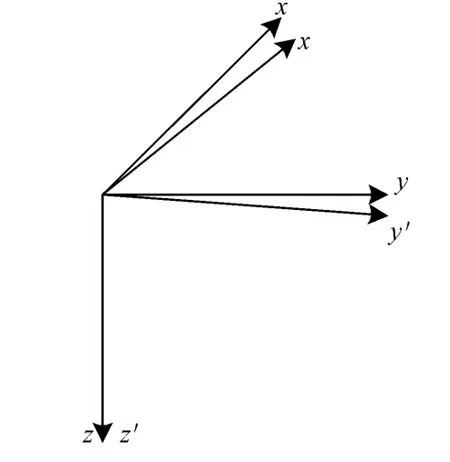
圖2 計算坐標示意圖

在上述計算坐標系中，磁場強度的三分量與各軸線圈驅動電流的關系如下．

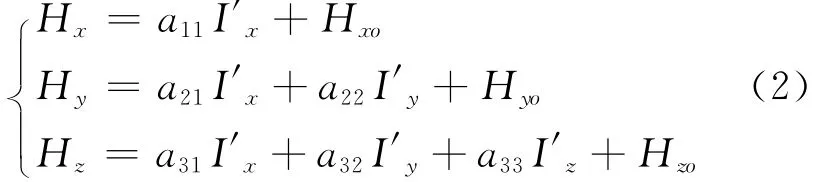
稱aij為三軸線圈的電磁系數．Hxo，Hyo，Hzo為本地地磁場在計算坐標系上的投影三分量．線圈電流系數和本地地磁場分量均可以預先精確求出．

為了精確模擬磁場矢量（Hx，Hy，Hz），對式（2）作線性變換如下．

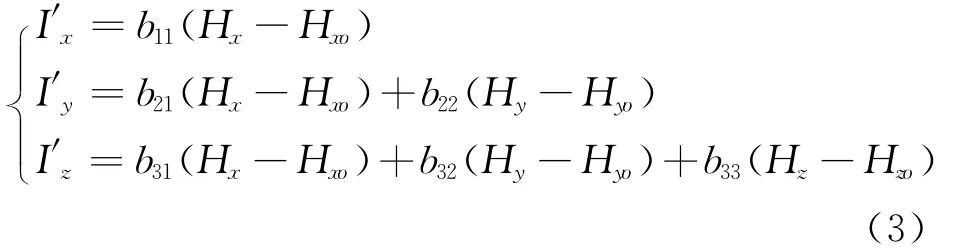
式中：

式（3）描述了線圈驅動電流 （I′x，I′y，I′z）與待模擬磁場（Hx，Hy，Hz）的對應關系．據此，可以根據所要模擬的磁場精確確定線圈驅動電流．

2 飛行器外部靜態磁環境模擬

為了求解飛行器干擾磁場的模型參數，應使飛行器殼體在地磁場中受地球磁場磁化，通過測量磁化產生的磁干擾數值，建立模型參數的回歸方程組，從而解出模型參數．從飛行器磁干擾模型的形式可以看出，建立回歸方程組最簡單的方法是不改變飛行地點，而改變飛行器相對于地磁場矢量的方向．

將飛行器安放在三軸線圈產生器的磁場均勻區中部，飛行器水平放置，頭部朝北，飛行器載體坐標系與磁場線圈的計算坐標系相同．

在載體坐標系中，所模擬固定點地磁矢量為

其中：－900≤θ≤900，00≤φ≤3600．式中：H為地磁場總強度，θ為相關于載體坐標系的磁傾角，φ為磁偏角．固定H值，改變θ和φ值，可以模擬飛行器在不同飛行姿態下受地磁場磁化的結果．

為了使模型參數的求解結果穩定，θ，φ樣本的選取應在其取值范圍內均勻分布，但考慮到用于檢測飛行器磁化狀態的光泵磁強計存在測量盲區，與被測磁場矢量的夾角不能太小，也不能接近垂直．將光泵磁強計的光軸豎直取向，則要求，

式中：θi，φj任意組合，構成48個樣本數據［θi，φj］，再由式（5）計算得到48組磁場矢量樣本數據．

令：N ＝6 M ＝8；記：k＝ （i－1）N＋j

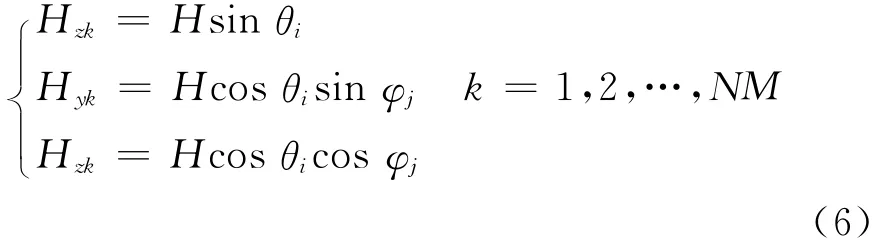
由式（6）的磁場樣本數據，利用式（3）可獲取相應的三軸線圈驅動電流如下：

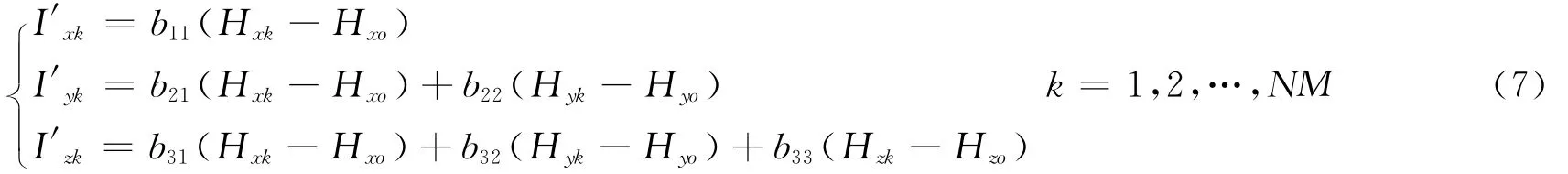
給三軸線圈加驅動電流 （I′xk，I′yk，I′zk），產生模擬磁場（Hxk，Hyk，Hzk）作用于飛行器殼體，產生飛行器在不同模擬姿態條件下的內部總磁場，使用光泵測出其大小．

此時飛行器殼體的背景磁場可表示如下：

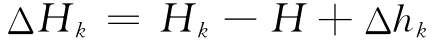
式中：Δhk為進行k次樣本試驗時的日變修正量，可使用另一臺光泵磁強計在一定距離外的參考測量點測量得到．

3 剩磁參數和感磁參數求解

3．1 模型系數方程

進行磁化試驗時，所加的磁場是靜態磁場，所以，產生的飛行器背景磁場中只有剩磁和感磁兩部分．因此有

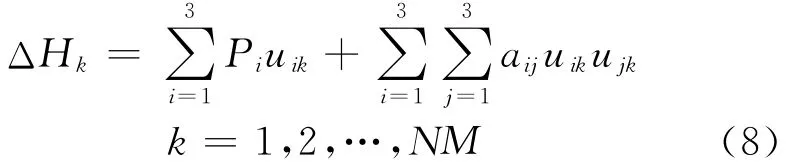
式中：

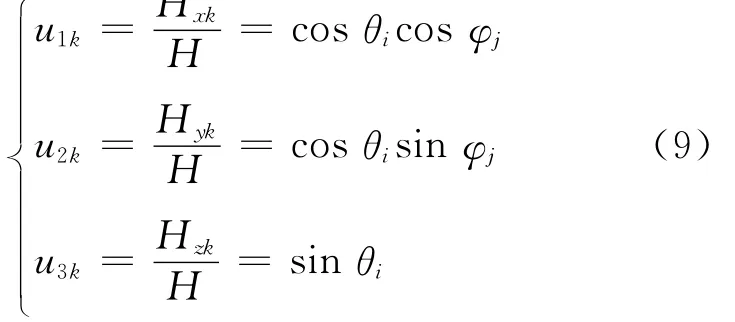
為地磁場方向余弦的樣本值；pi，i＝1，2，3為模型的剩磁系數；aij＝aji，a33＝0，i，j＝1，2，3為模型感磁系數．模型式（8）中有8個獨立變量．

在飛行器地磁導航應用領域，對磁場的測量精度要求不是很高，為1nT～10nT量級，而此時渦流磁場一般在1nT以下，此時忽略渦流磁場不會帶來太大誤差［7］．

3．2 模型定解條件

為了穩定求出模型的剩磁和感磁系數，必須有足夠的測量樣本數N×M，而且這些樣本必須滿足反映出地磁場從X，Y和Z3個方向對飛行器磁化的信息，從定解最低要求出發，至少應選擇磁傾角θj的兩個樣本，和磁方位角φj的四個樣本，構成8個樣本數據，但為了提高解的穩定性，樣本數可應選為獨立變量數的5～10倍，從而求解感磁和剩磁參數．一般情況下式（8）構成超定方程，可以用線性回歸方法求解．

4 仿真試驗結果與分析

根據飛行器磁干擾補償模型仿真試驗求解的算法仿真思路，首先設定飛行器磁干擾補償模型參數，用于模擬飛行器受地磁場磁化的規律，然后設定地磁場傾角和磁航向角，模擬飛行器的靜態磁環境，再由模型生成飛行器在靜態條件下的背景磁干擾數據，利用飛行器在靜態條件下的背景磁干擾數據求解出飛行器磁干擾補償模型的剩磁和感磁系數．

根據飛行器背景磁干擾的仿真數據樣本，對飛行器磁干擾模型參數進行求解，參數求解的結果及與真值對比如表1所列．

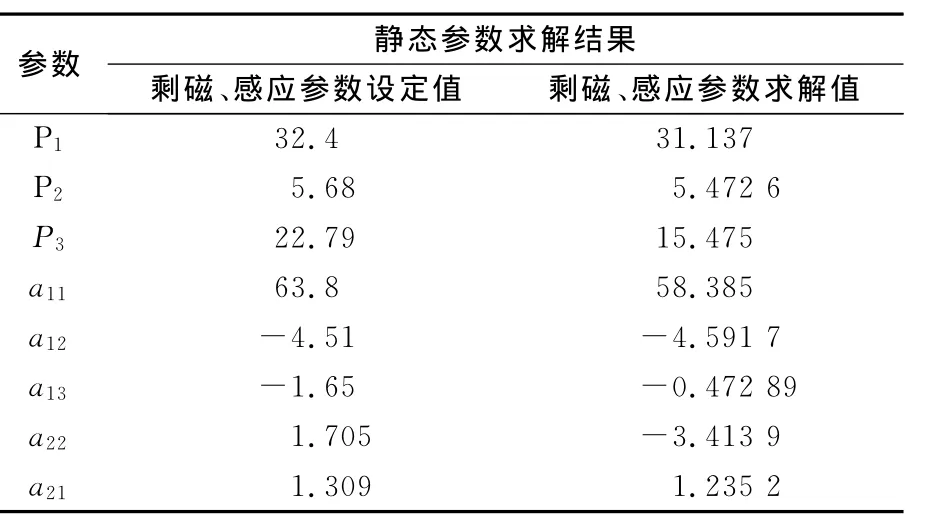
表1 模型參數求解結果

上述參數求解結果與參數設定值對比表明，算法的穩定性和精度良好，模型的偏差不超過10%．

5 結束語

為了能夠滿足飛行器的快速反應要求，本文在仿真試驗條件下對飛行器外部靜態磁環境進行模擬，通過計算機控制正交放置的三軸線圈驅動電流產生磁干擾數值，建立模型參數的回歸方程組，從而解出飛行器磁干擾模型中的剩磁和感磁參數，仿真試驗結果表明，飛行器外部靜態磁場的模擬精度較高，模型的偏差不超過10%，剩磁和感磁參數的求解精度和穩定性良好，能夠滿足飛行器的快速反應要求．

［1］鄧 鵬．譚 斌，林春生．飛行器外部磁場干擾補償的預處理［J］．海軍工程大學學報，2011，23（3）：58－61．

［2］譚 斌，林春生，張 寧，等．地磁場梯變對飛機磁場求解徑度的影響分析［J］．武漢大學學報：信息科學版，2011，36（12）：1482－1485．

［3］譚 斌，林春生，還迎春．地磁場水平梯度對飛機磁場干擾補償徑度的影響［J］．海軍工程大學學報，2012，24（6）：75－79．

［4］黎敏謙，陳菊秋，李 雪．三軸線圈磁體模擬產生艦船磁場的方法［J］．艦船電子工程，2011，31（1）：156－159．

［5］許 淼．三軸磁場模擬裝置的設計［D］．上海：上海交通大學，2012．

［6］袁楊輝．地磁導航中地磁變化場的研究［D］．武漢：華中科技大學，2012．

［7］龐學亮，王 清．高速飛行器背景磁場模型分析與改進［J］．四川兵工學報，2010，31（5）：22－24．