基于不確定性的線路退運模糊潮流計算

李暉，潘旭東，劉滌塵，吳軍，趙一婕，董飛飛

(1.國網北京經濟技術研究院，北京市100052;2.武漢大學電氣工程學院，武漢市430072)

0 引言

近年來，電網連鎖故障導致的大規模停電事故在世界范圍內頻繁發生，造成了巨大的經濟損失和嚴重的社會影響。因此，對不同線路的重要性進行評估，有效識別出重要線路并加強該區域的網架結構建設，對于提高電網的可靠性及避免造成大區域停電具有重要的意義。線路的重要性評估，可采用“單一線路退運后對系統造成的危害程度”這一標準，選取低電壓以及過負荷為指標，根據單一線路退運后系統運行狀態的變化來進行比選。電力系統作為典型的復雜、非線性系統，涉及許多不確定性因素，發電機出力、節點負荷很難被準確地確定，從而導致潮流分布不確定，因此，在進行線路退運后系統狀態的分析時有必要考慮這些不確定性因素。

文獻［1-2］采用區間分析方法來處理潮流計算中的不確定性因素，并進行了線路開斷后的分析，但是此方法只是應用在直流潮流計算中，并不能反映線路開斷后各節點電壓的變化。文獻［3］介紹了一種分析支路斷線的概率潮流方法，其對于負荷、發電機出力的不確定性均假設其服從某一分布函數，帶有較強的主觀性。

本文的主要目的是研究模糊理論在線路退運分析過程中不確定性處理的應用問題。應用模糊集理論中的梯形模糊數描述發電機出力、發電機可用度及預測負荷的不確定性，在前人研究計及不確定性的模糊潮流計算方法的基礎上，結合線路開斷的快速模擬算法中的靈敏度分析法，提出計及不確定性的線路退運后的模糊潮流算法。

1 發電機出力、發電機可用度及負荷不確定性的模糊描述

電力系統中的一些不確定性變量具有模糊特性，宜用模糊集合論中的模糊數描述［4-5］。當引入模糊集合論后，潮流計算中的一些運算將轉化為模糊數之間的運算。有關模糊數的定義及其運算見文獻［6］。

在模糊潮流計算中，發電機出力、發電機可用度以及負荷的不確定性可采用三角模糊數［7］或者梯形模糊數［8-9］表示。本文采用梯形模糊數描述，以負荷為例，某節點負荷的預測值可能出現在L1～L4之間，而最可能出現在L2～L3之間，負荷的這種不確定性可采用一個如圖1所示的梯形模糊數L4)表示，其隸屬函數為

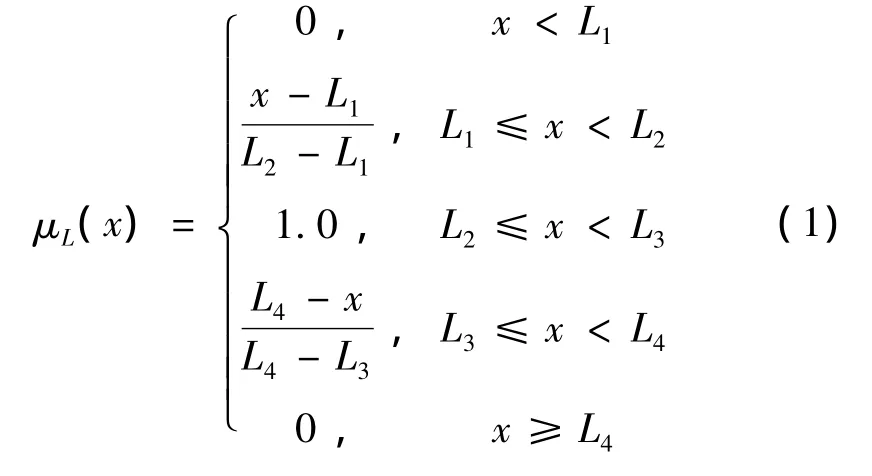
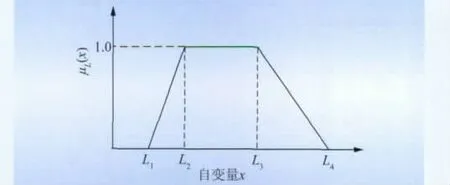
圖1 梯形模糊數Fig.1 Trapezoidal fuzzy numbers

模糊數中心值為 μL(x)=1.0截集的平均值

式中n為i節點上的發電機臺數。由模糊數的運算可知，~Pi、~Qi也是梯形模糊數。

2 線路開斷的靈敏度分析法

線路開斷的靈敏度分析法方法是將線路開斷視為正常運行情況的一種擾動，從電力系統潮流方程的泰勒級數展開式出發，導出了靈敏度矩陣，以節點注入功率的增量模擬斷線的影響，較好地解決了電力系統斷線分析計算的問題［10-12］。

根據牛頓潮流修正方程式:

式中:X0為狀態變量;Y0為網絡參數;f'x(X0，Y0)為雅可比矩陣;ΔW為節點不平衡功率。于是有

其中

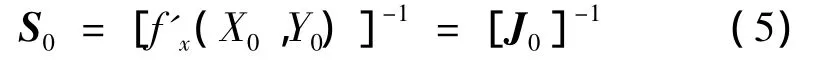
式中:S0為靈敏度矩陣;J0是牛頓潮流法中的雅可比矩陣。由于潮流計算中雅可比矩陣已經進行了三角分解，所以S0可以由回代過程求出。

若系統注入功率發生擾動為ΔW，或網絡發生變化ΔY，狀態變量也必然會出現變化，設其變化量為ΔX，并滿足方程

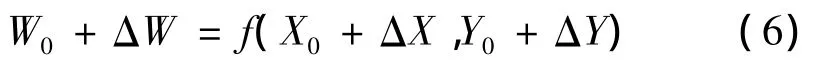
將上式按泰勒級數展開，忽略(ΔX)2項及高次項，且f(X，Y)是Y的線性參數，故f″yy(X，Y)=0，當不考慮節點注入功率的擾動時，ΔW=0，化簡可得到

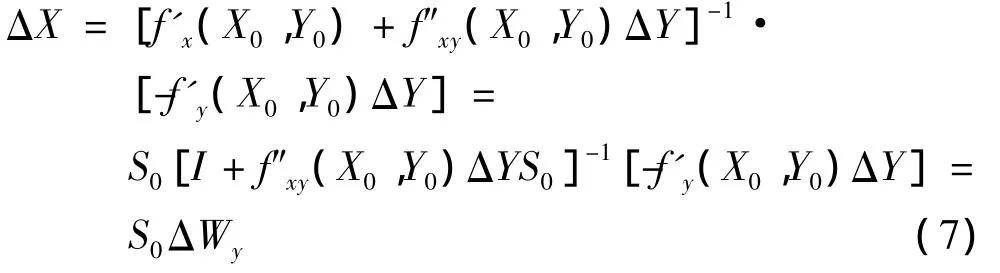
式中:I為單位矩陣;ΔWy可看成是支路開斷而引起的注入功率擾動。

本文僅考慮單條線路開斷的情況。假設開斷的支路兩端的節點i和j通過推導，最終寫成矩陣的形式為

式中:ΔPi、ΔQi、ΔPj、ΔQj為開斷線路 i、j時等效節點的注入功率均為靈敏度矩陣中行與列與斷線端點i、j有關的元素。

3 單一線路退運后的模糊潮流計算

本文在斷線分析的靈敏度法的基礎上，考慮不確定性因素的影響，提出了線路退運后的模糊潮流算法。由于利用靈敏度分析法進行斷線計算時，在求取斷線處的節點注入功率增量時所用到的H矩陣和潮流功率均與正常運行情況下的潮流計算有關，因此采用改進的增量法以求取線路退運后的模糊潮流計算(此處假設所斷線路兩端節點為P、Q節點)，其計算流程圖如圖2所示。

圖2 線路退運的模糊潮流計算方法流程Fig.2 Flowchart of fuzzy load flow calculation after line returned

其計算步驟如下:

(2)由增量法求解正常情況下電壓幅值、相角以及有功、無功功率的模糊增量。

采用牛頓－拉夫遜潮流算法時，可得

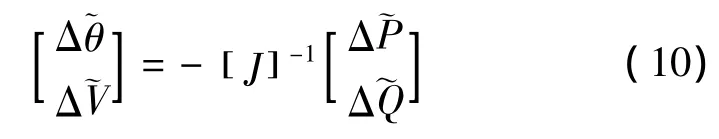
式中，雅可比矩陣[J]為確定性潮流計算時的最后一次迭代值。

已知支路的潮流方程為

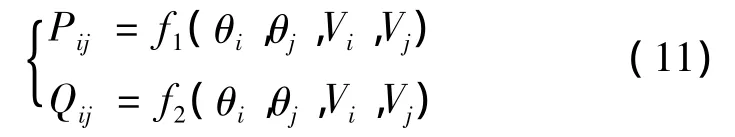
將其在某一運行點處(即中心點處)線性化，利用忽略二階及以上項的泰勒級數展開式，并考慮狀態變量增量的模糊性，則有

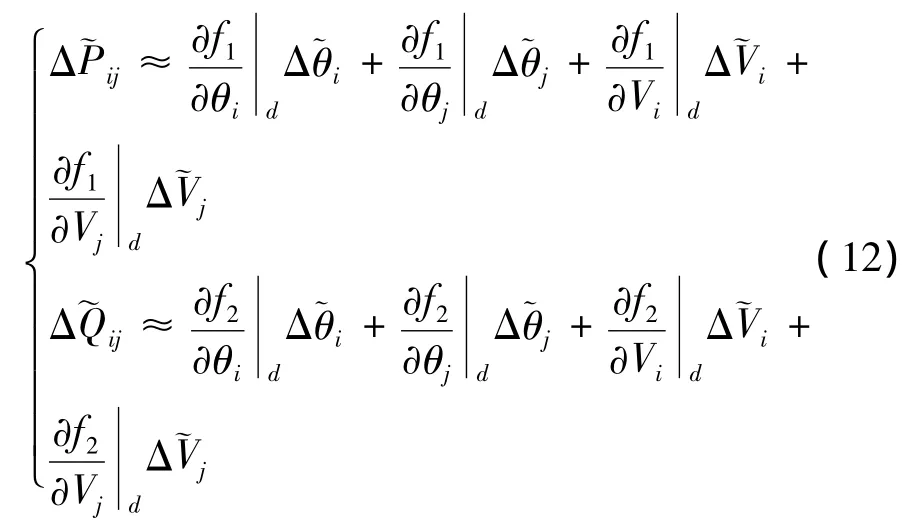
(4)利用節點模糊注入功率［~P］、［~Q］的中心值求取交流潮流方程時的最后一次迭代的雅可比矩陣中的元素來形成H矩陣，并利用步驟(3)中得到的有功、無功功率的梯形模糊數來形成ΔWl矩陣，于是，斷線處的節點注入功率增量可表示為

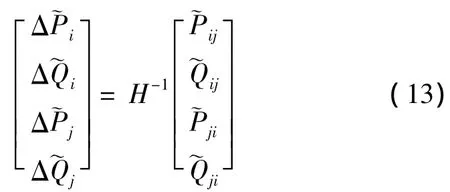
(5)根據斷線處的節點注入功率梯形模糊數求取線路開斷后引起的各節點電壓幅值和相角的模糊改變量，可由修正方程式求出。

(7)利用模糊數的運算法則，將正常運行下所求得的模糊潮流結果與線路退運后求得的節點電壓幅值、相角和有功、無功模糊增量進行疊加，進而可求出計及不確定性線路退運后各節點的電壓幅值和相角以及各支路有功功率、無功功率的梯形模糊數。

4 算例分析

利用本文研究的算法對IEEE－30節點系統進行線路退運后的模糊潮流計算。本算例中，模糊負荷及發電機模糊出力用梯形模糊數表示，其中對應μ(x)=0及μ(x)=1截集的極端值取為相應的中心值的(0.9，0.95，1.05，1.1)倍。基準容量 SB=100 MVA。

以線路3－4退運為例，由于篇幅所限，表1給出了部分計算結果。圖3、4分別給出了線路3－4退運后節點3的電壓梯形模糊圖以及線路2－6有功功率梯形模糊圖。

?

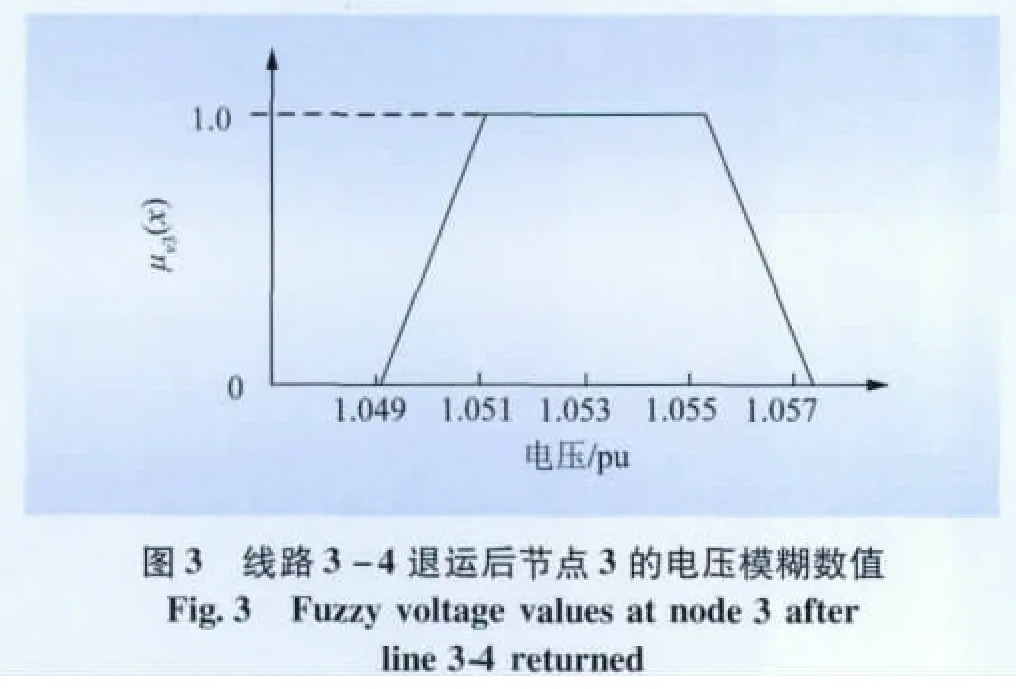
由圖3、4結果可看出:

圖4 線路3－4退運后線路2－6的有功功率模糊數值Fig.4 Fuzzy active power of line 2-6 after line 3-4 returned

當不考慮不確定性因素的影響時，對線路退運后進行分析得到的是電壓和功率的確定值;而在計及不確定性的基礎上，對單一線路退運之后進行模糊潮流計算，得到的是潮流(電壓、功率)的可能性分布，從而可以得到更為詳細的信息，如一些在不考慮不確定性因素影響時某一線路退運后并不會出現過負荷的線路或者不會出現低電壓的節點，而在計及不確定性時會有出現過負荷或者低電壓的可能。如圖4所示，當不考慮不確定性因素時，線路3－4退運后支路2－6的潮流功率為53.05 MW(如圖中P所示)，此時支路2－6有功功率小于線路最大傳輸功率55.09 MW(如圖4中Pmax點處，假定最大傳輸功率為正常潮流功率的1.4倍)，而當考慮不確定性因素后，由支路2－6的潮流分布可能性可以看出，支路2－6有可能發生過載，且是發生在較大的隸屬度μ(x)=1下。

此外，從梯形圖中還可看出線路發生過載的嚴重程度，例如當線路功率對應59 MW時，線路發生過載是處在較大的隸屬度下μ(x)=1下，且此時線路超過最大功率約4 MW，而這些是通過確定性潮流計算看不出來的。通過對各線路及節點變量的可能性分布進行分析，可為各線路單獨退運之后帶給系統的危害程度進行比較提供依據。

5 結論

本文研究了計及不確定性的線路退運后的模糊潮流計算方法，采用梯形模糊數處理負荷、發電機出力以及發電機可用度的不確定性，進行一次潮流計算便可得到單一線路開斷后潮流分布的可能性程度，同時可得出潮流功率過載以及節點電壓出現低電壓的可能性大小和嚴重程度，進一步結合風險評估的方法，便可為線路重要性大小排序提供依據。同樣計及不確定性，若仍沿用確定性潮流計算方法，對每一種情況都進行斷線分析，則可能需要進行上百次、上千次潮流計算，計算量過大。

［1］王守相，趙瑋，王成山，等.計及不確定性的預想事故自動選擇區間方法［J］.電力系統自動化，2007，31(20):27-31.

［2］武志峰.計及不確定性的電力系統靜態安全分析［D］.天津大學，2007.

［3］董雷，程衛東，楊以涵，等.考慮支路隨機斷線的概率潮流方法及應用［J］.電力系統保護與控制，2010，38(20):79-84.

［4］Miranda V，Saraiva J T.Fuzzy modelling of power system optimal load flow［J］.IEEE Trans on Power Systems，1992，7(2):843-849.

［5］Saraiva J T，Miranda V，Matos M A.Generation and load uncertainties incorporated in load flow studies［C］.6th Mediterranean Electrotechnical Conference Proceedings，V01.2:1339-1342.

［6］Kaufmann A，Gupta M M.Fuzzy mathematical models in engineering and management science［M］.North Holland ed，1988:32-40.

［7］張焰，陳章潮.電網規劃中的模糊潮流計算［J］.電力系統自動化，1998，22(3):20-22.

［8］張焰，陳章潮.計及不確定性的模糊交流潮流計算方法研究［J］.電網技術，1998，22(2):20-22，25.

［9］張焰，談偉.模糊潮流計算方法研究［J］.電工電能新技術，1999，18(3):9-12.

［10］王錫凡.現代電力系統分析［M］.北京:科學出版社，2003.

［11］王錫凡，王秀麗.實用電力系統靜態安全分析［J］.西安交通大學學報，1998，22(1):25-36.

［12］張偉，衛志農，劉玉娟.基于混沌優化的含風電場的最優潮流計算［J］.中國電力，2011，44(10):25-28.