炸藥顆粒床沖擊加熱多尺度數(shù)值計算

張新明，吳艷青，黃風雷

(北京理工大學 爆炸科學與技術國家重點實驗室，北京100081)

0 引言

塑料黏結炸藥(PBXs)可看作是一種特殊的顆粒復合材料，其主要組成部分包括HMX 含能顆粒(質量分數(shù)約占95%)、黏結劑、增塑劑及鈍感劑等(質量分數(shù)約占5%).PBXs 在受到沖擊加載時，HMX 炸藥顆粒為主要的承載對象，因此，在進行PBXs 沖擊起爆研究時，為了簡化模型，有時忽略黏結劑、增塑劑等的作用，將PBXs 看成由HMX 炸藥顆粒構成的顆粒床進行研究。另外，對于無空隙的均質含能材料，由于化學構成的不穩(wěn)定性、老化、損傷等因素會出現(xiàn)孔隙，研究這類材料的性能，也經常將它們看成顆粒炸藥床進行研究［1］。

燃燒轉爆轟(DDT)的研究已有幾十年的歷史［2-10］，也是顆粒含能材料受沖擊加載時常常產生的一個現(xiàn)象。文獻［3 -8］均表明顆粒含能材料的燃燒轉爆轟是顆粒材料的壓實(Material Compaction)和熱量釋放(Heat Release)的相互作用，而多數(shù)情況下，燃燒轉爆轟都與致密波(Compaction Wave)作用密切相關［11］。所謂致密波，即為使顆粒床孔隙率發(fā)生變化的行進波［11］，Sandusky 等［12］最早在試驗中觀察到穩(wěn)態(tài)致密波。在致密區(qū)內，由于顆粒與顆粒之間的摩擦、應力集中、塑性變形等原因會導致材料的局部溫度大幅升高，形成所謂的熱點(Hot-spot)，在整體平均溫度很低，甚至還沒達到熔點的情況下，就有可能使材料局部熔化，發(fā)生相變，激起劇烈的化學反應，并最終導致爆燃甚至是爆轟。自上世紀80年代始，國內外很多學者開展了這方面的實驗、理論和數(shù)值研究［13-19］。

但宏觀尺度的整體平均模型［13-17］不能有效地反映出顆粒尺度的響應，而基于單個顆粒的統(tǒng)計模型［18-19］由于計算量太大，不適合工程計算。近年來，Gonthier 等［20］根據(jù)Hertz 接觸力學建立了顆粒材料沖擊加熱的多尺度模型，該模型能夠有效地反映出顆粒尺度的響應，且適合大量工程計算。但是，Gonthier［20］沒有考慮顆粒可壓縮性和固液相變對壓縮過程的影響，并且顆粒構形應力函數(shù)由準靜態(tài)壓縮試驗測得，工作量大。本文選取Tait 狀態(tài)方程，由顆粒構形應力的定義式來確定該函數(shù)，避免進行大量試驗，從而減小工作量;同時引入化學反應進程變量，并考慮炸藥顆粒的可壓縮性以及固液相變的影響，對活塞沖擊顆粒床進行多尺度數(shù)值計算。

1 計算模型

Baer 等［7］的兩相流模型，通常稱為BN 模型，成為國內外學者研究致密波及含能材料燃燒轉爆轟基礎，本文在BN 模型的基礎上進行簡化，并結合顆粒尺度熱點模型和阿倫尼烏斯反應速率方程，對活塞沖擊顆粒床進行數(shù)值計算。

1.1 一維單相流模型

根據(jù)Baer 等［13］和Lovey 等［21］的工作，氣相對致密波的影響很小，本文忽略氣相作用，一維單相流模型如下:

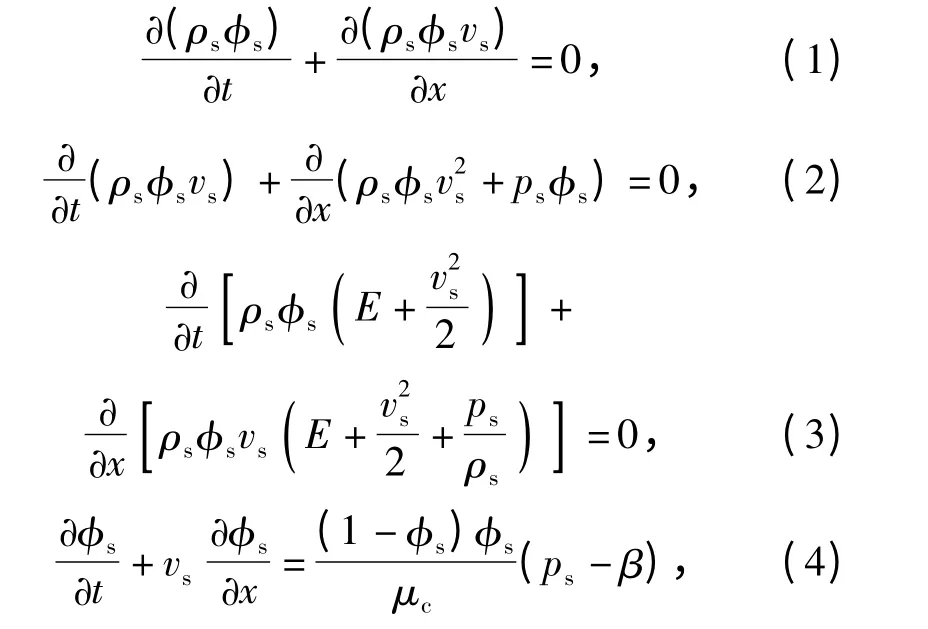
式中:t 為時間;x 為位置;ρs為固相密度;φs為固相體積分數(shù);vs為顆粒速度;ps為壓強;E 為單位體積炸藥的總能量，其中E =es+B，es為單位體積炸藥的內能，B 為單位體積炸藥的壓縮潛能;β 為顆粒構形應力函數(shù)，表示顆粒床受到擠壓后，顆粒之間的相互作用力;常數(shù)μc為壓縮粘性。(1)～(3)式分別為質量、動量和能量守恒方程;(4)式表示由于固相壓力與顆粒構形應力存在壓差而引起的固相體積分數(shù)的變化。

1.2 顆粒尺度的熱點模型

圖1為Gonthier［20］根據(jù)Hertz 接觸力學建立的熱點模型。圖中，rc為接觸球半徑，r0為接觸球半徑的最大值。當顆粒床受到外載荷時，顆粒與顆粒之間由于摩擦、應力集中、塑性變形等因素使得顆粒接觸面附近溫度升高，形成所謂的“熱點”，在整體平均溫度很低的情況下有可能發(fā)生燃燒轉爆轟。

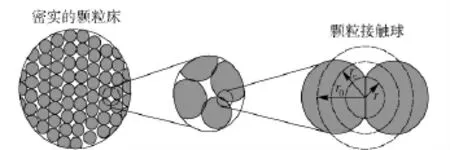
圖1 顆粒與顆粒間接觸的幾何模型Fig.1 Illustration of the intergranular contact geometry used for the thermal energy localization strategy

為簡化模型，假設HMX 顆粒不在發(fā)生破碎和聚并，顆粒半徑為R，單位體積內的顆粒數(shù)n，顆粒數(shù)守恒方程為

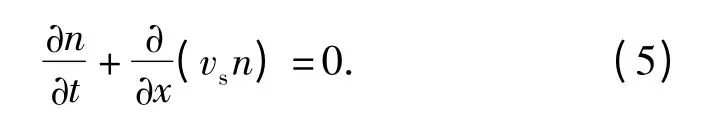
本文忽略顆粒與顆粒之間的摩擦作用，單位體積內塑性功功率等于內能的變化率，

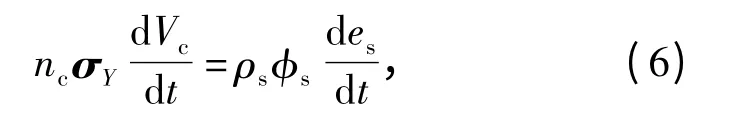
式中:nc為單位體積內的接觸球個數(shù);Vc=4/3r3c為單個接觸球的體積;σY=3.0Y 為塑形應力，Y 為HMX的屈服強度;des/dt 為內能變化率。

阿倫尼烏斯反應速率方程［20］

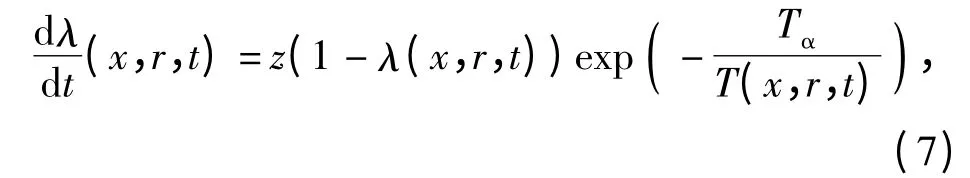
式中:λ(x，r，t)(0≤λ≤1)為沿接觸球徑向(r 方向，見圖1)變化的化學反應過程變量，λ =0 表示無化學反應發(fā)生，λ=1 表示完全反應;z 為阿倫尼烏斯因子;Tα為活化溫度。

內能變化率

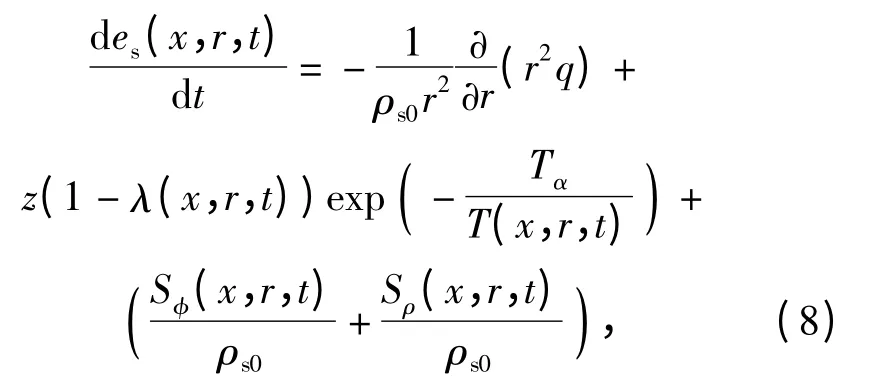
式中:q 為傳導熱通量，q = -k ?T(x，r，t)/?r，k 為熱傳導率;ρs0為固相初始密度。(8)式右端第1 項為由熱傳導引起的內能變化率，第2 項為由化學反應引起的內能變化率，第3 項為由顆粒材料孔隙率變化引起的內能變化率Sφ以及由顆粒密度變化引起的內能變化率Sρ.

HMX 在常溫常壓下的熔點T0m為552 K，根據(jù)Kraut-Kennedy［22］關系，熔點Tm= T0m(1 +αΔV/V0)，其中，常數(shù)α =1.53，V 為比容，V0為初始比容;在ps≈5 GPa 的條件下，ΔV≈0.1，熔點升高到約636 K，而本文條件下ps?5 GPa，因此假設Tm=T0m，顆粒床發(fā)生等溫相變:

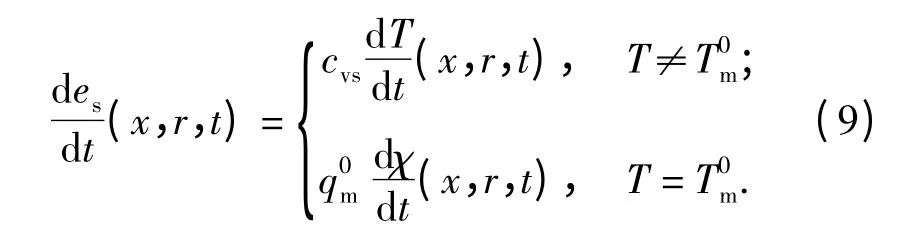
式中:cvs為定容比熱;q0m為熔化潛熱;0≤χ≤1 為液相質量分數(shù)。

1.3 本構關系

為使方程組封閉，還需要給出固相狀態(tài)方程和顆粒構形應力函數(shù)β.本文對Powers 等［23］給出的狀態(tài)方程進行修改，引入化學反應進程變量λs，Helmholtz 自由能的表達式為:

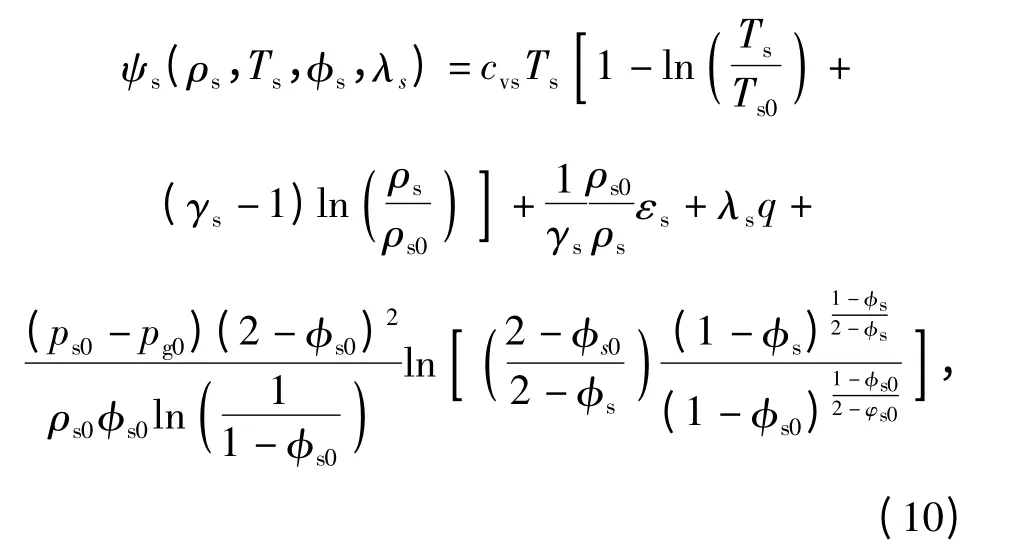
式中:Ts0為固相初始溫度;ps0為固相初始壓強;pg0為氣相初始壓強;φs0為固相初始體積分數(shù)。

狀態(tài)方程

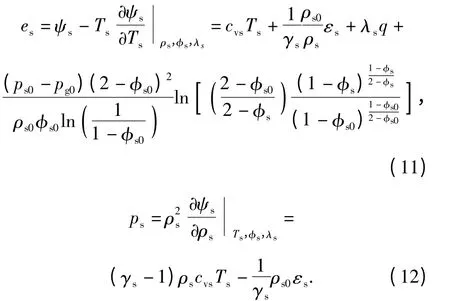
顆粒構形應力函數(shù)β 的表達式如下:

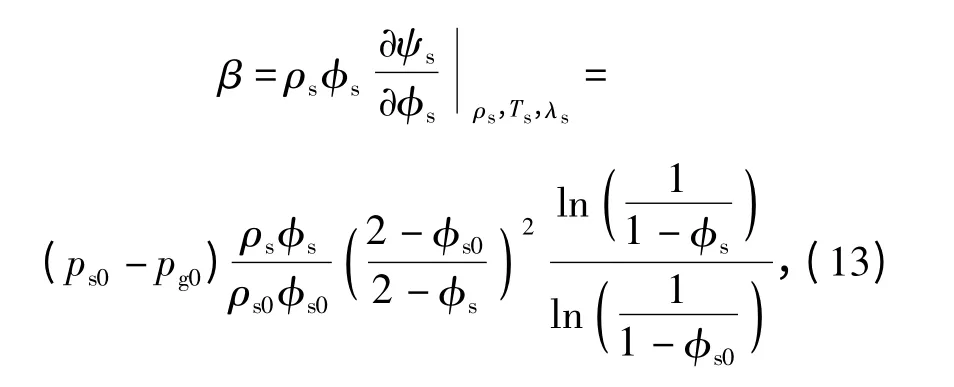
Tait 狀態(tài)方程中的參數(shù)如表1所示。

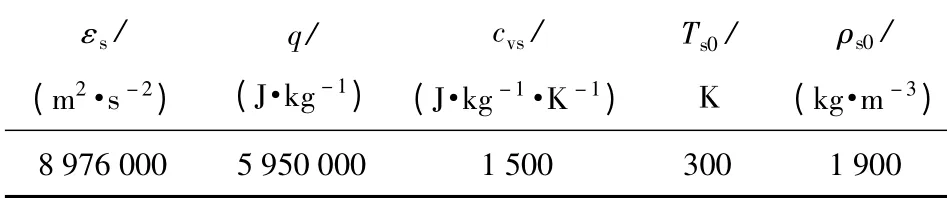
表1 Tait 狀態(tài)方程中的參數(shù)Tab.1 Parameters in Tait EOS for solid HMX

2 計算模型的無量綱化

本文以HMX 顆粒為例，對其致密波傳播特性進行分析，表2為HMX 的物性參數(shù)及初始條件。

表2 HMX 物理性質參數(shù)及初始條件Tab.2 HMX material properties and initial conditions

假設致密波以波速D 向右傳播，利用伽利略坐標變換公式:相對位置ξ=x-D·t 和相對速度v=vs-D 以及定常假設，?/?t ≡0.定義如下無量綱量:

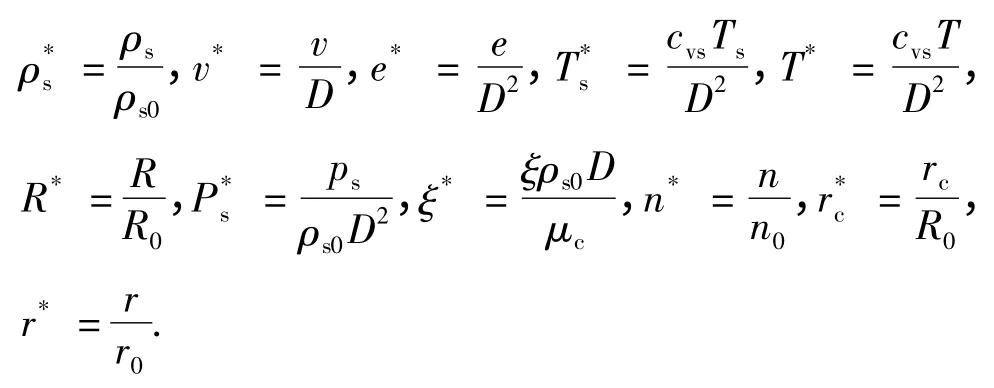
將計算模型寫成無量綱形式

3 計算結果

為確定壓縮過程的終態(tài)，令β =ps，即顆粒床達到壓力平衡。圖2為顆粒構形應力函數(shù)β 與固相體積分數(shù)φs之間的關系。由圖可知，β 為體積分數(shù)φs的單調遞增函數(shù)。圖3為不同致密波速D，固相壓力Ps與體積分數(shù)φs之間的關系。由圖可知，隨著致密波速度的增加，終態(tài)體積分數(shù)φs逐漸增加，當D ＞500 m/s 時，終態(tài)體積分數(shù)φs≈1，即顆粒床處于完全壓實狀態(tài)。

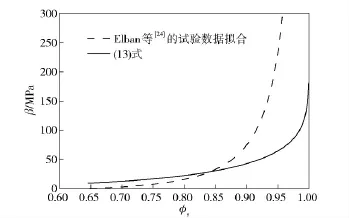
圖2 顆粒構形應力β 與固相體積分數(shù)φs之間的關系Fig.2 Intergranular stress β vs.solid volume fraction φs

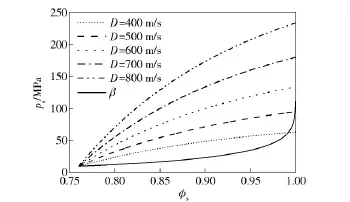
圖3 固相壓力ps與固相體積分數(shù)φs之間的關系Fig.3 Solid pressure ps vs.solid volume fraction φs

3.1 惰性顆粒藥床

圖4 初始體積分數(shù)φs0 =0.76，活塞速度up =100 m/s 時模型物理量在ξ 方向上的分布Fig.4 Variation of model parameters in ξ direction for φs0 =0.76 and up =100 m/s

圖4為活塞速度up=100 m/s 撞擊顆粒藥床，產生亞音速致密波(D=418.7 m/s ＜C0)，固相體積分數(shù)φs、壓力ps、顆粒間的應力β、整體平均溫度Ts和顆粒密度ρs的分布。由圖4可知，各物理量由初始狀態(tài)光滑地過渡到平衡狀態(tài)，終態(tài)值φs=0.995，ps=67.73 MPa，Ts=304.08 K，ρs=1 906.62 kg/m3.由圖4(b)可知，在初始階段顆粒床處于平衡狀態(tài)，即Ps0=β(φs0)，隨著活塞向右運動，壓力增加，顆粒間構形應力增加，當ps=β(φs)時，顆粒床再次達到壓力平衡狀態(tài)。

圖5為up=100 m/s 撞擊顆粒床時，顆粒半徑R、接觸球半徑rc和顆粒溫度T 的分布。由圖5(a)可知，壓縮過程中顆粒半徑R 幾乎保持不變，接觸球半徑rc由初始值rc0≈1.859 8 μm 光滑地過渡到穩(wěn)態(tài)值rc≈4.849 4 μm;由圖5(b)可知，由于顆粒之間的擠壓，發(fā)生塑性變形，在顆粒接觸面附近，顆粒溫度明顯升高，最大值T≈973 K，超過了HMX 的熔點T0m=552 K，并可以觀察到相變發(fā)生。而由圖4(c)可知，相同的加載條件下，整體平均溫度Ts≈304 K，遠低于顆粒尺度溫度的最大值，即整體平均模型不能有效地反應顆粒尺度的響應。

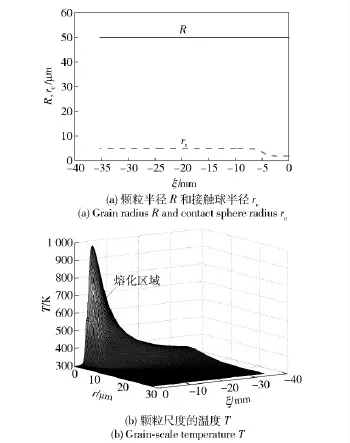
圖5 顆粒半徑和顆粒尺度溫度的分布(up =100 m/s)Fig.5 Variation of grain radius in ξ direction and grainscale temperature in ξ and radial directions at up =100 m/s

3.2 考慮化學反應

圖6為考慮固相可壓縮性和相變的情況下，化學反應進程變量λ、顆粒溫度T、整體平均反應進程變量λs和整體平均溫度Ts的分布。由(19)式可知，由于考慮了固相可壓縮性，接觸球半徑rc會增大，這就意味著內能將會分布在顆粒接觸面附近更大的區(qū)域上，從而使顆粒溫度降低;另外由于相變會消耗掉一部分能量，也將使顆粒溫度降低，因此在相同的初始條件下要激發(fā)化學反應必須增大活塞速度。當活塞速度up=79.0 m/s 時，致密波速度D=348.75 m/s，由圖6(a)和圖6(b)可知，在顆粒接觸面附近化學反應進程變量λ =1，即完全反應，相應地溫度出現(xiàn)了突跳，顆粒溫度的最大值為1 638 K，并且可以觀察到相變的發(fā)生。由圖6(c)和圖6(d)可知，整體平均化學反應進程變量λ≈7.5 ×10-7，整體平均溫度Ts≈302.5 K.結果再次表明整體平均模型不能有效地反應顆粒尺度的響應。

3.3 參數(shù)研究

圖7為活塞速度up、初始體積分數(shù)φs0、顆粒半徑R 等模型參數(shù)對顆粒床壓縮過程的影響。由圖7(a)可知，隨著活塞速度up的增加，固相體積分數(shù)φs逐漸增加，up～φs曲線的斜率逐漸減小，表明顆粒床更難被壓實;當活塞速度up＞100 m/s 時，固相體積分數(shù)φs≈1，即顆粒藥床被完全壓實。圖7(b)為活塞速度up與致密波速度D 之間的關系，由圖可知，隨著活塞速度up的增加，致密波速度D 逐漸增加，且兩者之間近似成線性關系。由圖7(c)可知，隨著初始體積分數(shù)φs0的增加，要想激起化學反應，所需壓力逐漸增加;當φs0＞0.90 時，所需壓力急劇增加，也即致密的顆粒床更難發(fā)生化學反應。由圖7(d)可知，隨著顆粒半徑R 的增加，激起化學反應所需的活塞速度逐漸減小，即粗顆粒床更容易發(fā)生化學反應，這一結果與已有的試驗和數(shù)值模擬結果［25-28］相一致。

4 結論

本文對活塞沖擊HMX 顆粒床進行多尺度數(shù)值模擬。結果表明，對于亞音速致密波，固相體積分數(shù)、壓力、密度和整體平均溫度光滑地從初始值過渡到平衡狀態(tài)，致密波速度隨著活塞速度的增加而逐漸增加，顆粒床的致密程度隨著致密波速度的增加而增加，直到藥床被完全壓實(φs≈1).顆粒尺度的溫度分布表明，在相同的加載條件下(up=100 m/s)，顆粒尺度的溫度明顯高于整體平均溫度，并超過了熔點，同時可以觀察到固液相變的發(fā)生，結果表明整體平均模型不能有效地反映出材料顆粒尺度的響應。在考慮化學反應的情況下，由于顆粒材料可壓縮性和固液相變的影響，在相同的初始條件下，必須增大活塞速度才能激起化學反應。計算結果還表明，隨著固相初始體積分數(shù)的增大，發(fā)生化學反應所需的外界載荷越大，即致密床更難發(fā)生化學反應;隨著顆粒半徑的增大，發(fā)生化學反應所需的活塞速度越小，即粗顆粒床更容易發(fā)生化學反應。

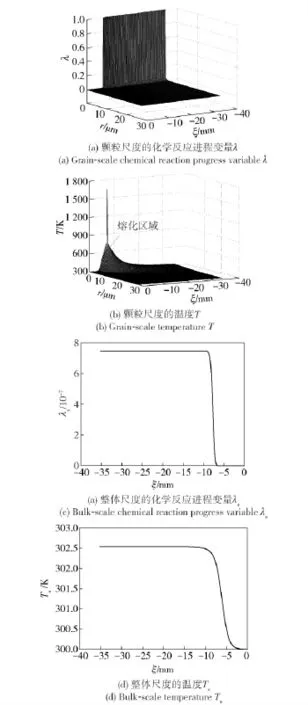
圖6 化學反應進程變量和溫度的分布Fig.6 Predicted chemical reaction progress variable and temperature through the compaction zone

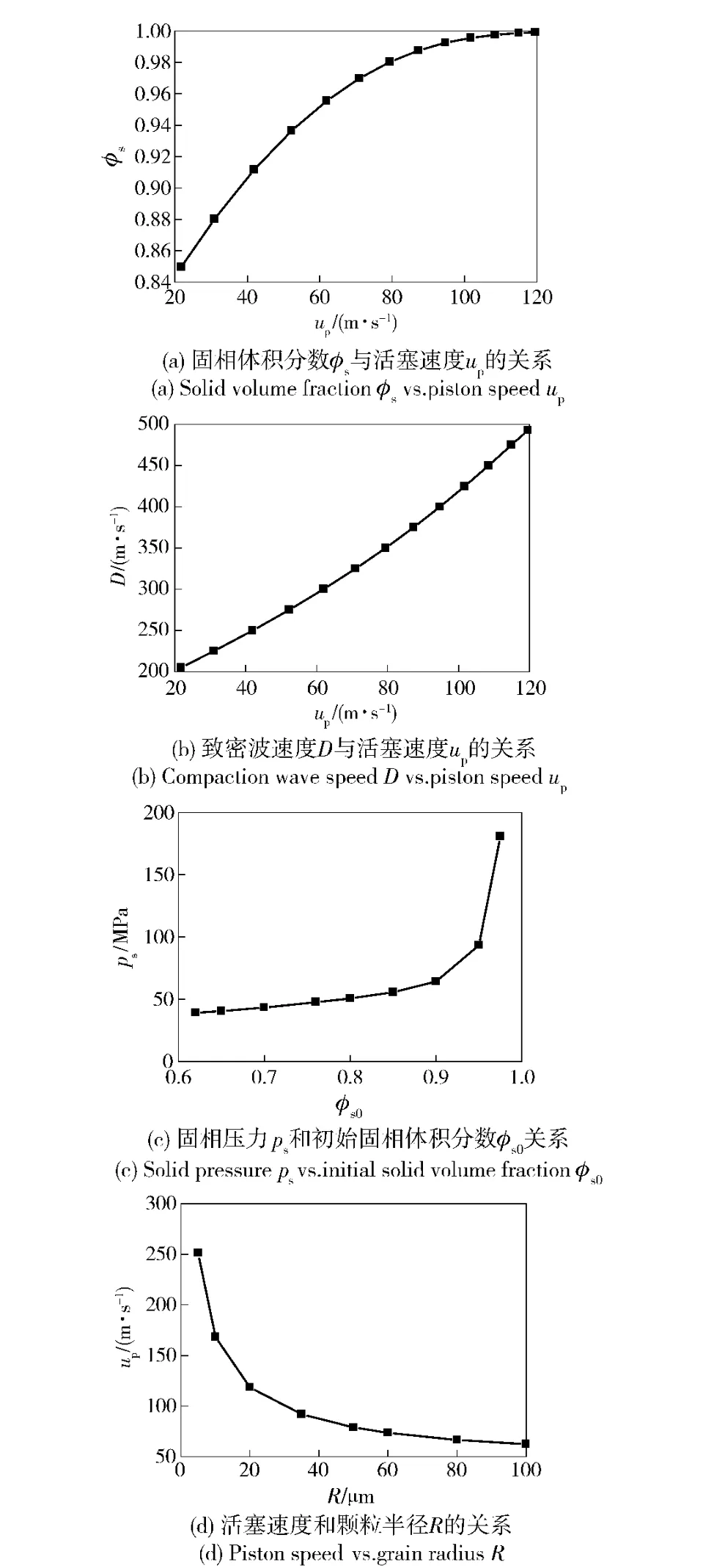
圖7 模型參數(shù)研究Fig.7 Parametric sensitivity analysis results

References)

［1］ Greenaway M W.Measurement of intergranular stress and porosity during dynamic compaction of porous beds of HMX［J］.Journal of Applied Physics，2005，97(9):093521 -093521-7.

［2］ Gonthier K A，Powers J M.A high resolution numerical method for a two-phase model of deflagration-to-detonation transition［J］.Journal of Computational Physics，2000，163(2):376 -433.

［3］ Cochran M T，Powers J M.Computation of compaction in compressible granular material［J］.Mechanics Research Communications，2008，35(1 -2):96 -103.

［4］ Bernecker R R，Price D.Studies in the transition from deflagration to detonation in granular explosives-Ⅰ.Experimental arrangement and behavior of explosives which fail to exhibit detonation［J］.Combust and Flame，1974，22(1):111 -118.

［5］ Bernecker R R，Price D.Studies in the transition from deflagration to detonation in granular explosives-Ⅱ.Transitional characteristics and mechanics observed in 91/9 RDX/wax［J］.Combust and Flame，1974，22(1):119 -129.

［6］ Butler P B，Krier H.Analysis of deflagration to detonation transition in high-energy solid propellant［J］.Combust.Flame，1986，63(1 -2):31 -48.

［7］ Bear M R，Nunziato J W.A two-phase mixture theory for the deflagration to detonation transition (DDT)in reactive granular materials［J］.International Journal of Multiphase Flow，1986，12(6):861 -889.

［8］ Xu S J，Stewart D S.Deflagration-to-detonation transition in porous energetic materials:a comparative model study［J］.Journal of Engineering Mechanics，1997，31(2 -3):143 -172.

［9］ Kapila A K，Menikoff R，Bdzil J B，et al.Two-phase modeling of deflagration-to-detonation transition in granular materials:reduced equations［J］.Physics of Fluids，2001，13(10):3002 -3024.

［10］ Butler P B，Krier H.Modeling deflagration to detonation transition in granular explosives pentaerythritol tetranitrate［J］.Journal of Applied Physics，2008，104(4):043519-(043519-14).

［11］ Powers J M，Stewart D S，Krier H.Analysis of steady compaction waves in porous materials［J］.Journal of Applied Mechanics，1989，56(1):15 -24.

［12］ Sandusky H W，Liddiard T P.Dynamic compaction of porous beds［R］.US:Naval Surface Warfare Center Silver Spring MD，1985.

［13］ Baer M R.Numerical studies of dynamic compaction of inert and energetic granular materials［J］.Journal of Applied Mechanics，1988，55:36 -43.

［14］ Gonthier K A，Menikoff R，Son S E，et al.Molding compactioninduced energy dissipation of granular HMX［C］∥11th Symposium (International)on Detonation.1998:153 -161.

［15］ 孫錦山，朱建士，賈祥瑞.顆粒材料中致密波結構研究［J］.力學學報，1999，31(4):423 -433.SUN Jin-shan，ZHU Jian-shi，JIA Xiang-rui.An analysis of compaction wave in granular material［J］.Journal of Theoretical and Applied Mechanics，1999，31(4):423 -433.(in Chinese)

［16］ Low C A，Greenaway M W.Compaction process in granular beds composed of different particle sizes［J］.Journal of Applied Physics，2005，98(12):123519-(123519 -12).

［17］ Low C A，Longbottom A W.Effect of particle distribution on the compaction behavior of granular beds［J］.Physics of Fluids，2006，18(6):066101-(066101 -18).

［18］ Menikoff R，Kober E.Compaction waves in granular HMX［J］.Shock Compression of Condensed Matter，1999，505:397 -400.

［19］ Bardenhagen S G，Brackbill J U.Dynamic stress bridging in granular material［J］.Journal of Applied Physics，1998，83(11):5732 -5740.

［20］ Gonthier K A.Modeling and analysis of reactive compaction for granular energetic solids［J］.Combustion Science and Technology，2003，175:1679 -1709.

［21］ Lovey A，Ben-Dor G，Sorek S，et al.Jump conditions across strong compaction waves in gas saturated rigid porous media［J］.Journal of Shock Waves，1993，(3):105 -111.

［22］ Menikoff R，Sewell T D.Constituent properties of HMX needed for mesoscale simulations［J］.Combustion Theory and Modeling，2002，(6):103 -125.

［23］ Powers J M.Two-phase viscous modeling of compaction of granular materials［J］.Physics of Fluids，2004，16(8):2975 -2990.

［24］ Elban W L，Chiarito M A.Quasi-static compaction study of coarse HMX explosive［J］.Power Technology，1986，46(2 -3):181 -193.

［25］ Moulard H，Kury J W，Declos A.The effect of RDX particle size on the shock sensitivity of cast PBX formulations［C］∥8th Symposium (International)on Detonation.1985:902 -913.

［26］ Moulard H.Particular Aspect of the explosive particle size effect on shock sensitivity of cast PBX formulations［C］∥9th Symposium (International)on Detonation.1989:18 -24.

［27］ Simpson R L，Helm F H，Crawford P C，et al.Particle size effects in the initiation of explosives containing reactive and nonreactive continuous phases［C］∥9th Symposium (International)on Detonation.1989:25 -38.

［28］ Gustavsen R L，Sheffield S A，Alcon R R.Low pressure shock initiation of porous HMX for two grain size distribution and two densities［J］.American Institute of Physics，1996，370:851 -854.