參數修改對鐵電薄膜相變性質的影響*

盧兆信

(臨沂大學機械工程學院，臨沂 276005)

(2012年12月20日收到;2013年2月1日收到修改稿)

1 引言

近年來，由于薄膜制備技術日益發展成熟及其在各種領域中的廣泛應用，一直以來鐵電薄膜都是實驗制備和理論研究的熱點之一[1-3].迄今為止，對鐵電薄膜的理論研究主要有兩種方法：一種是采用朗道-德文希爾的唯象理論[4-9]，另一種是采用微觀理論的橫場伊辛模型[10-13].橫場伊辛模型通常被用來描述有序—無序型鐵電體的相變，現在已被成功地應用于對鐵電薄膜相變性質的研究，比如BaTiO3和SrTiO3薄膜[2,3].薄膜中存在的尺寸效應和表面效應都會顯著地影響它的相變性質.因為橫場伊辛模型不能被精確地求解，導致許多近似方法被用來計算薄膜的相變性質，比如平均場近似[10-24]、格林函數方法[25,26]和關聯有效場理論[27-31].關聯有效場理論是一種基于自旋關聯和微分算子技術并且相當于澤爾尼克近似的方法，Kaneyoshi[27]對其進行改進和推廣，使其成功地用來研究橫場伊辛薄膜的各種相變性質.同時，Kaneyoshi[28]進一步將平均場近似、關聯有效場理論和退耦合近似三種理論方法進行了比較，結果表明關聯有效場理論是一種優于平均場近似的方法，利用它計算時可以得到比平均場近似更為精確的結果.最近Arhchoui等[30]和我們研究小組[31]分別利用關聯有效場理論對雙表面鐵電薄膜的相變性質進行了討論.但據我們所知，利用關聯有效場理論針對多表面層的鐵電薄膜(Ns＞2)的相變性質的研究還沒有開展過.

本文將針對任意層(N)的具有不同表面層(Ns)的鐵電薄膜系統，利用微分算子技術來研究表面橫場、表面層數和薄膜層數對薄膜各相互作用參數從FPD到PPD過渡值和參數空間中各相變區域的影響.同時也將把本文的計算結果與平均場近似進行比較.

2 模型和公式

2.1 理論模型

本文所要研究的鐵電薄膜系統是由任意N層的簡立方結構沿z方向構成，每一層被定義在x-y平面內，贗自旋處于平面中的正方晶格內，如圖1所示.薄膜各層被標記以 1，2，3，···，N，將第 1，2，3，···，Ns層和第 N-(Ns-1)，···，N-1，N 層定義為薄膜系統的2Ns個表面層，而剩下的N-2Ns層則被定義為體內層.對于一個只發生二級鐵電相變的薄膜系統其哈密頓量為[31]

圖1 任意N層的鐵電薄膜系統的結構示意圖

2.2 公式

根據關聯有效場理論可知，薄膜第i層中贗自旋的平均值為[31]

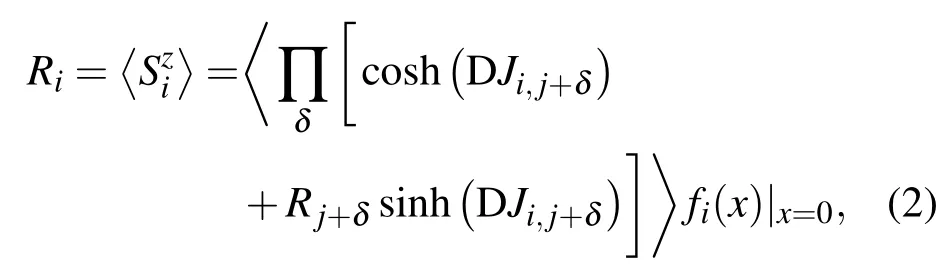
其中，∏表示對格點i取其所有最近鄰格點的乘積，D=?/?x表示微分算子，滿足關系式exp(αD)f(x)=f(x+α).在表面層中，函數 fi(x)被定義為

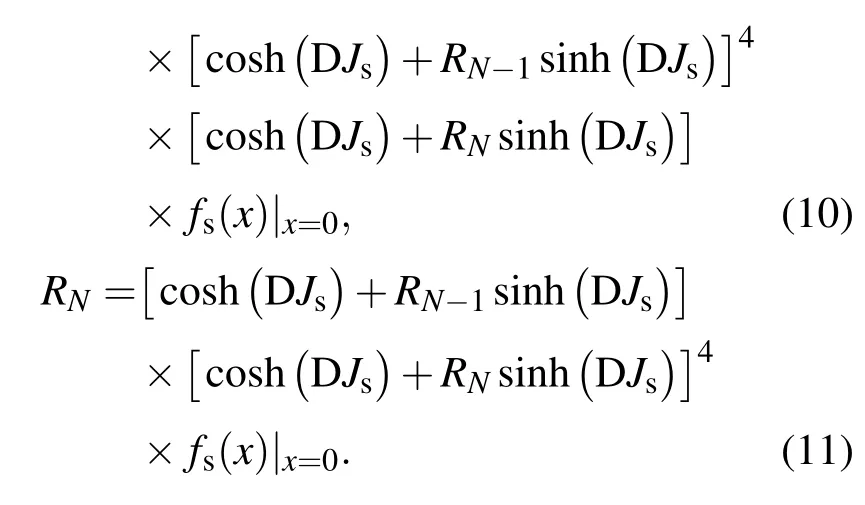
當溫度無限趨近于居里溫度時，可以將上面的N個方程展開，只保留Ri的線性項，而Ri的非線性項則忽略不計.最終可以推導得到計算任意層(N)的具有不同表面層(Ns)鐵電薄膜系統相圖的解析通式方程

3 數值計算結果和討論

通常情況下，鐵電薄膜相圖的描述有兩種方法：一種是用Js-Tc關系曲線表示的相圖，另一種是用Ωs-Tc關系曲線表示的相圖.選擇合理的體內交換相互作用、表面橫場、體內橫場、表面層數和薄膜層數，就可以利用方程(12)計算任意層(N)的具有不同對稱表面層(Ns)的薄膜的相圖，下面本文將選擇利用Js—Tc關系曲線來描述的相圖進行研究.

3.1 表面層數對各相互作用參數過渡值的影響

對于一個用Jrms-Tc關系曲線來描述的薄膜相圖來說，主要由體內相互作用Jb、表面橫場Ωs、體內橫場Ωb、表面層數Ns和薄膜層數N來決定.在相圖中Js-Tc關系曲線將其分成兩個相變區域，左側為鐵電相區域，右側為順電相區域.根據Teng等的定義[20,25]，可以薄膜各相互作用參數(Jb，Ωs和Ωb)中的任意一個為自變量，而其他兩個相互作用參數的數值保持不變，適當地調整自變量的數值，當相圖由鐵電相占主導地位的相圖(ferroelectricdominant phase diagram，FPD)轉變為順電相占主導地位的相圖(paraelectric-dominant phase diagram，PPD)時，有可能存在表面相互作用Js和居里溫度Tc同時趨向于零的一個臨界狀態，將此時刻該自變量的值稱之為其使相圖由FPD到PPD的過渡值.

圖2展示的是當鐵電薄膜的體內層數Nb一定時，表面層數Ns對其各相互作用參數過渡值的影響.從圖2(a)中可以看到，以體內相互作用Jb為自變量而保持表面橫場Ωs和體內橫場Ωb固定不變時，當從FPD到PPD時，存在Js和Tc同時趨向于零的臨界狀態，同時可以發現圖2(a)中存在一個顯著的特性，即表面層數Ns的改變對體內相互作用Jb的過渡值是沒有影響的，也就是說體內相互作用的過渡值Jbc不依賴于表面層數Ns的，這與平均場近似的結果是完全一致的[23].另外從圖2(a)中可以看到，當表面層數Ns≥2時，隨著Ns的增加，相圖中的鐵電相區域減小，順電相區域增加，最終趨向于Ns=1時的結果.所以當Ns≥2時，表面層數Ns的增加可以在某種程度上消減鐵電薄膜的鐵電性，并且趨向于Ns=1時的情況，這與平均場近似的結果是完全不同的[23].而圖2(b)，(c)分別展示的是當薄膜的體內層數Nb一定時，表面層數Ns對表面橫場Ωs和體內橫場Ωb的過渡值的影響，顯然與對體內相互作用Jb過渡值的影響完全類似.

3.2 表面橫場、表面層數和薄膜層數對參數空間中各相變區域的影響

為了獲取描述鐵電薄膜相變性質的概圖，根據Wang等所采取的ST方法[11]，以表面橫場Ωs/Jb和薄膜層數N作為參數將薄膜系統的相變性質用(Js/Jb，Ωb/Jb)平面內的相圖來描述.采用ST方法可以非常方便地將參數空間(Js/Jb，Ωb/Jb)平面內的相圖分為三個相變區域：表面極化增加的區域E(Tc( film)＞Tc(bulk))、表面極化降低的區域R(Tc( film)＜Tc(bulk))和順電相區域P.事實上，利用ST方法來描述的相圖實質上展示的是在不同的相互作用參數下的Js—Tc關系曲線.為了方便與平均場近似的結果進行比較[11]，下面的計算中選取的表面橫場Ωs/Jb和薄膜層數N與文獻[11]中完全相同.

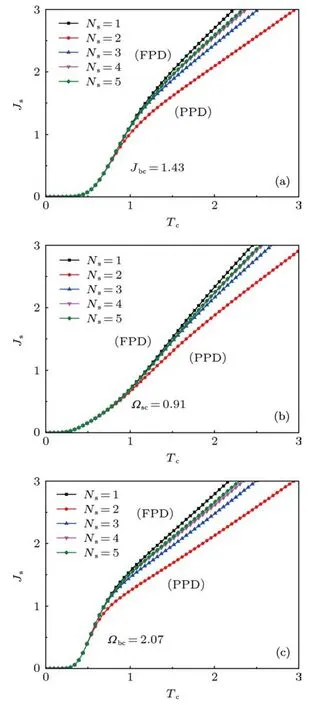
圖2 表面層數對鐵電薄膜各相互作用參數過渡值的影響 (Nb=3)(a)Ωs=2.0，Ωb=3.0;(b)Jb=2.0，Ωb=4.5;(c)Jb=1.0，Ωs=2.0

圖3展示的是當表面層數為單表面(Ns=1)時，表面橫場Ωs/Jb和薄膜層數N對參數空間(Js/Jb，Ωb/Jb)中各相變區域的影響.從圖3(a)中可以看到，對一個表面橫場Ωs/Jb和薄膜層數N確定的薄膜系統來說，當體內橫場Ωb/Jb比較小時，從參數空間中的左側下方開始系統處于R區域.隨著體內橫場Ωb/Jb的增加并到達某一臨界值時，系統將處于P區域.隨著表面交換相互作用Js/Jb的增加，R/P區域的分界線是逐漸上升的.與此相類似，在參數空間中的左側下方，隨著表面交換相互作用Js/Jb的增加，當它變得足夠大在1和2之間時，系統會處于E區域.隨著體內橫場Ωb/Jb的增加，R/E區域的分界線逐漸下降至比較小的表面交換相互作用Js/Jb，最終與R/P區域的分界線相交，這在一定程度上反映了表面橫場Ωs/Jb是固定的事實.從圖3(b)中可以看到，當體內橫場Ωb/Jb比較小時，在R/E區域分界線上的表面交換相互作用Js/Jb隨著表面橫場Ωs/Jb的增加而增加.顯然，對比圖3(a)，(b)可以發現，隨著表面橫場Ωs/Jb的增加，整個R/E區域的分界線移動到比較大的表面交換相互作用Js/Jb處.同時，在圖3中存在著一個顯著的特性，即R/E區域的分界線是不依賴于薄膜層數N的，而R/P區域的分界線則是依賴于薄膜層數N的，隨著薄膜層數N的增加，P區域反而減小.上述性質與平均場近似是完全類似的[11]，但是數值大小則是完全不同的.

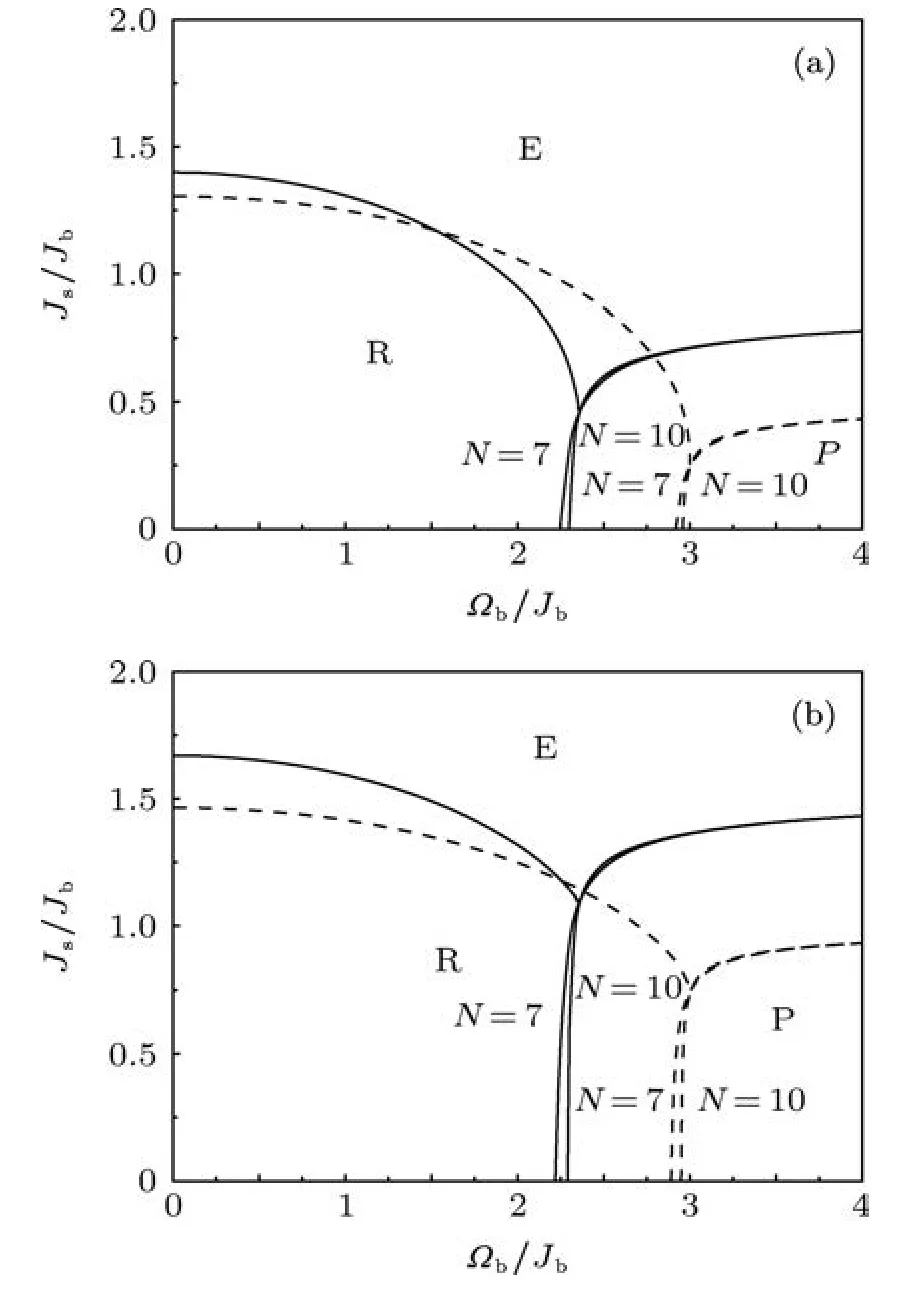
圖3 在參數空間(Js/Jb，Ωb/Jb)平面內的單表面(Ns=1)鐵電薄膜系統相圖(虛線為平均場近似的結果) (a)Ωs/Jb=1;(b)Ωs/Jb=2

同時，在圖3中可以清晰地看到關聯有效場理論與平均場近似的區別，顯然利用關聯有效場理論計算得到的順電相區域P要大于平均場近似，而鐵電相區域則小于平均場近似，這表明參數空間中的鐵電相區域在某種程度上被平均場近似過分的估計了，也就是說關聯有效場理論可以在一定程度上消減鐵電薄膜被平均場近似所夸大的鐵電性.

圖4展示的是當表面層數為雙表面(Ns=2)時，表面橫場Ωs/Jb和薄膜層數N對其參數空間(Js/Jb，Ωb/Jb)中各相變區域的影響.與圖3比較可以發現，對一個相同體內橫場Ωb/Jb來說，參數空間中各相變區域之間的分界線下降到一個比較低的表面交換相互作用Js/Jb處.另外，對表面層數Ns分別為3和4的薄膜在參數空間(Js/Jb，Ωb/Jb)中的各相變區域也進行了計算，結果表明這些相變區域仍然存在，這也都與平均場近似完全類似[11].

圖4 在參數空間(Js/Jb，Ωb/Jb)平面內的雙表面(Ns=2)鐵電薄膜系統相圖(虛線為平均場近似的結果) (a)Ωs/Jb=1;(b)Ωs/Jb=2

4 結論

綜上所述，在關聯有效場理論的框架內，利用微分算子技術，系統地分析和討論了表面橫場、表面層數和薄膜層數對多表面鐵電薄膜各相互作用參數過渡值和參數空間中各相變區域的影響.結果表明，薄膜各相互作用參數由FPD到PPD的過渡值是不依賴于表面層數的，而參數空間中的各相變區域卻緊密的依賴于表面橫場、表面層數和薄膜層數.與平均場近似進行比較的結果顯示，關聯有效場理論可以在某種程度上削減平均場近似對鐵電薄膜鐵電性的夸大.希望本工作可以為相應的實驗研究提供一些理論依據或指導.

感謝山東大學物理學院王春雷教授對本論文的指導.

[1]Scott J F 2007 Science 315 954

[2]Damjanovic D 1998 Rep.Prog.Phys.61 1267

[3]Dawber M，Rabe K M，Scott J F 2005 Rev.Mod.Phys.77 1083

[4]Zhong W L，Wang Y G，Zhang P L，Qu B D 1994 Phys.Rev.B 50 698

[5]Lu T Q，CaoW W 2002 Phys.Rev.B 66 24102

[6]Lin S，Lu T Q，CaoW W 2006 Phys.Stat.Sol.(b)243 2952

[7]Sun P N，CuiL，Lu T Q 2009 Chin.Phys.B 18 1658

[8]Zhou Z D，Zhang C Z，Zhang Y 2010 Acta Phys.Sin.59 6620(in Chinese)[周志東，張春祖，張穎2010物理學報59 6620]

[10]Wang C L，Zhong W L，Zhang P L 1992 J.Phys.:Condens.Matter 4 4743

[11]Wang C L，Smith S R P，Tilley D R 1994 J.Phys.:Condens.Matter 6 9633

[12]Sy H K 1993 J.Phys.:Condens.Matter 5 1213

[13]Wang X G，Pan S H，Yang G Z 1999 J.Phys.:Condens.Matter 11 6581

[14]TaoY M，Jiang Q，CaoH X 2005 Acta Phys.Sin.54 0274(in Chinese)[陶永梅，蔣青，曹海霞2005物理學報54 0274]

[15]Sun P N，Lu T Q，Chen H，CaoW W 2008 Chin.Phys.Lett.25 3422

[16]Chen H，Lu T Q，CuiL，CaoW W 2008 Physica A 387 1963

[17]Zhou J，Lu T Q，Xie W G，CaoW W 2009 Chin.Phys.B 18 3054

[18]CuiL，Lu T Q，Sun P N，Xue H J 2010 Chin.Phys.B 19 077701

[19]CuiL，Xu Q，Han Z Y，Xu X 2012 Chin.Phys.Lett.29 037701

[20]Teng B H，Sy H K 2004 Physica B 348 485

[21]Lu Z X，Teng B H，Lu X H，Zhang X J，Wang C D 2009 Solid State Commun.149 1176

[22]Lu Z X 2013 Phys.Scr.87 025002

[23]Lu Z X 2012 Physica A(submitted)

[24]WeiG Z，Liu J，MiaoH L，Du A 2007 Phys.Rev.B 76 054402

[25]Teng B H，Sy H K 2004 Phys.Rev.B 70 104115

[26]Lu Z X，Teng B H，Yang X，Rong Y H，Zhang H W 2010 Chin.Phys.B 19 127701

[27]KaneyoshiT 1993 Acta Phys.Pol.A 83 703

[28]KaneyoshiT 2003 Physica A 319 355

[29]Jiang W，LoV C 2008 Physica A 387 6778

[30]ArhchouiH，ElAmraouiY，Mezzane D，Luk’yanchuk I 2009 Eur.Phys.J.Appl.Phys.48 10503

[31]Lu Z X，Teng B H，Rong Y H，Lu X H，Yang X 2010 Phys.Scr.81 035004