若干高階微分方程的解
甘欣榮,甘泉
(1.武漢科技大學 理學院,湖北 武漢 430065;2.武漢大學 電子信息學院,湖北 武漢 430079)
微分方程在物理學及控制論或許多領域中有著廣泛的應用,能否求出微分方程的解析解,一直是科研人員感興趣的問題.加之高階微分方程的求解可供操作的方法較少,有些甚或無法求出具體解.文[1]提出2類新的高階微分方程,借助函數迭代法及分析原理,得出它們的求解公式.本文將文[1]的定理1作為下面的引理.
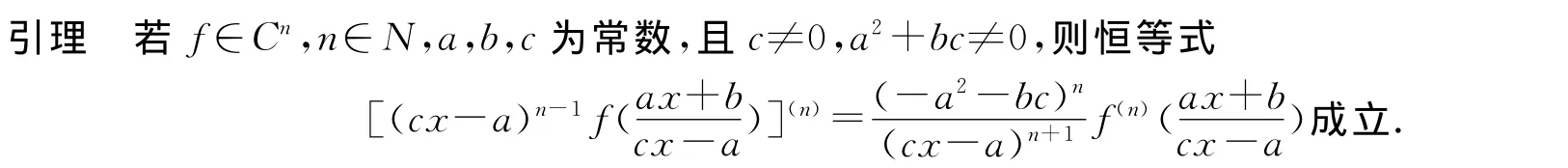
利用文[2-3]的有關技巧,把文[1]的2個結論略作改進,得到幾種新的高階微分方程的求解定理,進一步深化了高階微分方程解的范圍.
1 主要結論



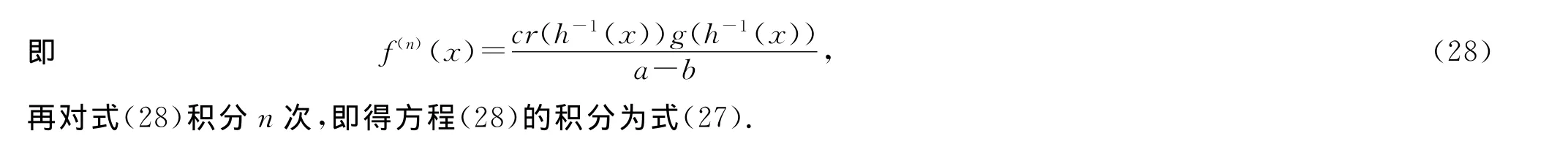
2 應用

[1]湯光宋.高階非線常微分方程的可積類型[J].華中師范大學學報:自然科學版,1995,29(1):20-23.
TANG Guangsong.Integrable Types of higher-order non-linear ordinary differential equations[J].Journal of Central China Teachers University:Natural Science Edition,1995,29(1):20-23.
[2]湯光宋,瞿國林.新高階常微分方程的可積類型[J].浙江海洋學院學報:自然科學版,1999,18(4):335-339.
TANG Guangsong,QU Guolin.Integrality of new higher order differential equation[J].Journal of Zhejiang Ocean University:Natural Science Edition,1999,18(4):335-339.
[3]馮錄祥.一類 Riccati型方程的通積分[J].數學的實踐與認識,2000,30(2):235-239.
FENG Luxiang.The integral of the equation of Riccatitype[J].Mathematics in Practice and Theory,2000,30(2):235-239.
[4]甘欣榮.積分微分方程組的若干求解公式[J].大學數學,2008,24(6):137-141.
GAN Xinrong.Some solution seeking formula for integral differential equation sets[J].College Mathematics,2008,24(6):137-141.
[5]湯光宋,馮麗珠.常微分方程專題研究續論[M].武漢:武漢出版社,2007.
TANG Guangsong,FENG Lizhu.Continuous discussion on ordinary diferential equation monographic study[M].Wuhan:Wuhan Press,2007.
[6]鐘壽國.Mobius變換中的n階循環群判據[J].南京師大學報:自然科學版,2011,34(4):17-20.
ZHONG Shouguo.N-order circle group criterion of Mobius transformation[J].Journal of Nanjing Normal University:Natural Science Edition,2011,34(4):17-20.
[7]王培光,李志芳.含causal算子分數階非線性微分方程的擬線性方法[J].河北大學學報:自然科學版,2012,32(1):1-6.
WANG Peiguang,LI Zhifang.Quasilinearization for solution of nnlinear Causal fractional differential equations[J].Journal of Hebei University:Natural Science Edition,2012,32(1):1-6.
[8]甘欣榮,鐘壽國.M 變換中的n階循環群判定[J].鄭州大學學報:理學版,2012,44(3):25-28.
GAN Xinrong,ZHONG Shouguo.Determing the cyclic group of order n in Mobins transformation[J].Journal of Zhengzhou University:Natural Science Edition,2012,44(3):25-28.

