井壁漂浮下沉期應變分析

梁旭黎，李方紅，楊志江

（1.石家莊經濟學院 勘查技術與工程學院，河北 石家莊 050031；2.石家莊經濟學院 水資源與環境學院，河北 石家莊 050031；3.中國礦業大學 力學與建筑工程學院，江蘇 徐州 221008）

目前在中國鉆井法廣泛應用于深厚表土層鑿井工程中，井筒支護質量的優劣直接影響到整個鉆井工程的質量，乃至今后豎井的使用，有關井壁破壞造成重大安全事故的報道屢見不鮮，因此對井壁受力分析的研究意義非常重大［1－4］.本文以河北省唐山市某礦豎井工程為背景，對施工過程中井壁漂浮下沉期井壁的應變進行了彈性力學分析與數值分析，并將二者與實測數據進行了對比，分析了漂浮下沉期井壁應變的變化規律，為深入進行此類研究探索提供參考.

1 工程概況

河北省唐山市某豎井工程采用鋼筋混凝土井壁，鉆井法施工.地層情況為：0～238.90m主要為砂層和卵礫石層，238.90～251.40m為風化黑云角閃斜長片麻巖，251.40～286.55m為黑云角閃斜長片麻巖.井筒設計凈直徑為6.2m，井壁結構參數及力學參數見表1.

表1 井壁結構參數及力學參數Tab.1 Structure parameters and mechanical parameters of shaft lining

2 彈性力學分析

在深厚表土層中的井壁是典型的長柱狀厚壁圓筒結構，彈性力學中圓筒受均布壓力的拉麥公式［5］

式中，σθ，σr分別為計算斷面井壁的環向應力和徑向應力，MPa；r，R，ρ分別為井壁內、外半徑和計算點半徑，m；P0為永久地壓，P0＝1.2H×10－2，H為地表下一點的深度，m均布壓力作用下的內應力分布見圖1.

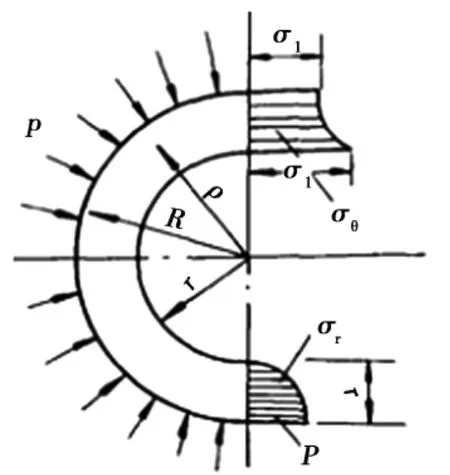
圖1 均布壓力作用下的內應力Fig.1 Internal stress in the effect of uniform pressure

井壁漂浮下沉階段，井壁任意水平斷面外側承受泥漿水平壓力qn，豎向承受上部井壁自重應力qz，當配重水位超過該水平斷面之后，該斷面還將在內側承受配重水壓力qw.

泥漿壓力計算式為

式中，γn為泥漿重度，由實測確定；Hn為計算斷面的下沉深度.

配重水計算式為

式中，γw為配重水重度，γw＝10 000N／m3；Hw為計算斷面與配重水之間的距離，m.

式中，W為上部井壁重力，A為斷面面積.

因此，井壁任意水平斷面圓環應力解為承受內外壓厚壁圓筒平面應力的應力解與豎向應力的疊加，即

式中，σz為計算斷面井壁的豎向應力，MPa.σθ，σr，r，R，ρ同式（1）.

根據軸對稱問題的物理方程

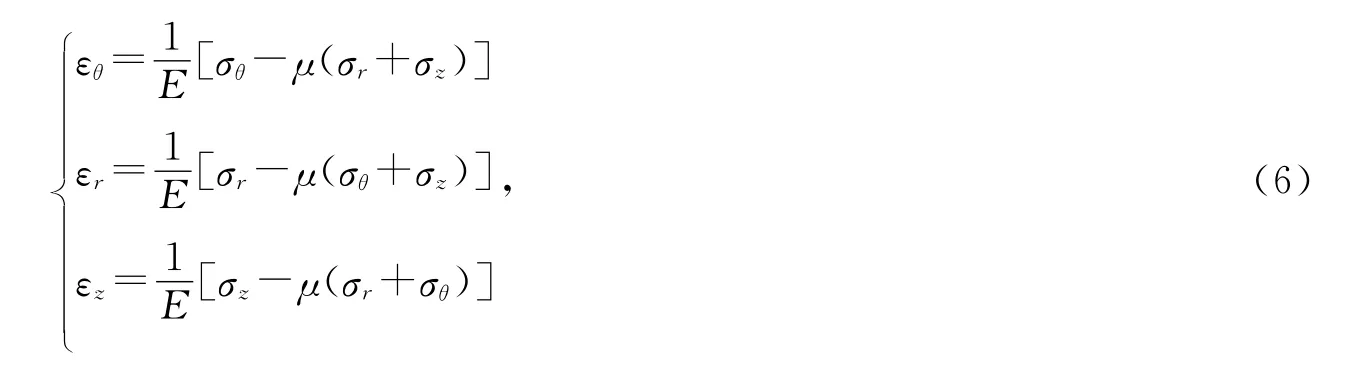
由式（5），（6）可得井壁任意斷面應變

式中，εθ，εr，εz分別是計算斷面井壁環向、徑向和豎向應變；E為井壁混凝土彈性模量，MPa；μ為井壁混凝土泊松比.

由于井壁具有環向受力為主的受力特點，因此以井壁的環向應變計算為例，進行彈性力學求解.全文取第4節井壁中部斷面為例，R＝3.7m，r＝3.1m，E＝36 000MPa，μ＝0.2，A＝12.81m2，由式（6）中εθ的表達式可計算出第4節井壁漂浮下沉過程中環向應變的值.井壁任意斷面的環向應變值均可用相同方法計算.

例如，當第4節井壁下沉到底時，其中部斷面的Hn＝267.5m，根據泥漿對井壁的浮力與井壁的自重和配重水之和相平衡的原理可計算出此時Hw＝180.6m，實測γn＝11 500N／m3，根據施工資料，第5－57節井壁總質量m＝7 525t，計算出qz＝5.91MPa.由式（6）計算出εθ＝－245×10－6.第4節井壁漂浮下沉過程中，其中部斷面的環向應變彈性力學計算結果見表2.

表2 環向應變彈性力學計算值Tab.2 Elasticity calculation values of circumferential strain

3 漂浮下沉過程數值模擬

采用有限元計算軟件，就井壁漂浮下沉過程受力做了數值模擬，以便與彈性力學計算值與實測數據進行對比分析.計算采用空間軸對稱模型，按實際井壁進行建模，計算模型見圖2，有限元網格見圖3.各段井壁不考慮鋼筋，僅按素混凝土考慮，考慮井壁上下法蘭，上下段井壁之間粘接.

圖2 井壁計算模型Fig.2 Calculation model of the shaft lining

圖3 井壁有限元網絡Fig.3 Finite element mesh of the shaft lining

井壁幾何參數和力學參數見表1.井壁底考慮內外層鋼板，不考慮錨卡.鋼板彈性模量為210GPa，泊松比0.25，密度7 800kg／m3.

通過數值模擬可獲得井壁底鋼板和各節井壁環向應變和豎向應變值.

4 計算結果對比與分析

將第4節井壁中部斷面環向應變彈性力學計算值、數值計算值與實測值進行對比，見圖4.將第4節井壁中部斷面豎向應變數值計算值與實測值進行對比，見圖5.

圖4 環向應變彈性力學計算值、數值計算值與實測值比較Fig.4 Comparison between elasticity calculation values，numerical calculation curves and measured curves of circumferential strain

圖5 豎向應變數值計算值與實測值Fig.5 Comparison between numerical calculation values and measured curves of vertical strain

從圖4中看出，第4節井壁中部斷面的環向應變彈性力學計算值、數值計算值和實測值均反映出隨著下沉深度的加大，環向應變的值也加大，二者幾乎呈線性分布；彈性力學計算值、數值計算值和實測值吻合較好.從圖5中看出，豎向應變的數值計算值和實測值吻合較好.將圖4與圖5對比后發現，在井壁的漂浮下沉過程中，環向應變遠大于豎向應變，這說明了井壁環向受力大于豎向受力，井壁以環向受力為主，這也是本文以環向應變的彈性力學求解為例來進行應變分析的原因，豎向應變的彈性力學求解方法與環向應變相同.從彈性力學計算值、數值計算值與實測值基本吻合，可以說明本文中所采用的彈性力學計算方法和數值模擬方法均可以對豎井施工中漂浮下沉過程各節井壁的受力進行分析.

井壁底板受力非常復雜，數值計算值與實測值對比后發現差別太大，在本文中不做分析.

5 結論

1）由井壁任意水平斷面圓環應變解，對唐山某豎井工程施工中漂浮下沉過程井壁的環向應變進行了彈性力學求解；通過有限元數值計算，對井壁漂浮下沉過程受力做了數值模擬，獲得了環向應變與豎向應變解答，環向應變大于豎向應變.

2）將彈性力學計算值、數值計算值與實測值進行了對比，結果表明，彈性力學計算值、有限元數值計算值與實測值基本吻合，均反映出應變值隨井壁漂浮下沉深度的增大而增大，二者幾乎呈線性分布.

3）井壁的彈性力學計算值、有限元數值計算值與實測值基本吻合，可為類似工程提供參考.井壁底板的有限元數值計算值與實測值相差很大，需要進一步分析.

［1］張永成，孫杰，王安山.鉆井技術［M］.北京：煤炭工業出版社，2008.

ZHANG Yongcheng，SUN Jie，WANG Anshan.Drilling technology［M］.Beijing：Coal Industry Press，2008.

［2］崔廣心.深厚表土層中圓筒形凍結壁和井壁的力學分析［J］.煤炭科學技術，2008，36（10）：17－21.

CUI Guangxin.Mechanical analysis on cylindrical freezing wall and mine shaft liner in deep thick overburden［J］.Coal Science and Technology，2008，36（10）：17－21.

［3］楊志江，梁旭黎，王華明，等.施工期鉆井井壁混凝土應變實測分析［J］.煤炭學報，2011，36（9）：1463－1468.

YANG Zhijiang，LIANG Xuli，WANG Huaming，et al.Insitu measurement and analysis of drilling shaft lining concrete strain during sinking［J］.Journal of China Coal Society，2011，36（9）：1463－1468.

［4］牛學超，洪伯潛，楊仁樹.充滿配重水鉆井井壁筒在泥漿中豎向結構穩定的理論研究［J］.煤炭學報，2005，30（4）：463－466.

NIU Xuechao，HONG Boqian，YANG Renshu.Theory study on axial structural stability of bored shafts filled with water［J］.Journal of China Coal Society，2005，30（4）：463－466.

［5］徐芝綸.彈性力學［M］.北京：高等教育出版社，2005.