基于觀測器的風力發電系統滑模變結構控制

徐 紅，劉東樂

（燕山大學電氣工程學院，秦皇島066004）

隨著風力發電技術的不斷發展，風力發電機不僅在單機發電技術上得到了提高，而且經過整合后輸送到大電網的電能也變得更加安全可靠，其中變速恒頻技術在當前的風力發電運行中應用最為廣泛[1，2]。但是在風速高于風力機額定風速時，如何才能更穩定、更安全地實現恒頻發電，已成為目前風電專家們的研究熱點。近年來，針對風電機組槳距角控制技術的優化研究有很多。文獻[3]通過深入分析風電系統變槳距控制技術，針對風速高與額定風速時的控制性能，采用了基于傳統PI控制算法的增益調節策略，使變槳距控制系統得到很大改善；文獻[4]設計了變槳距模糊邏輯控制器，并且與帶轉矩觀測器的控制增益法和增益查表法做了對比分析；文獻[5]中針對槳葉節距角控制問題，提出以風輪轉速為反饋信號的PI 控制器，使風電機組實現了變速恒頻運行控制；文獻[6，7]對于如何改善異步機風電場的暫態電壓穩定性，提出了建立靜止無功補償器SVC （static var compensator）控制模型和風電機組槳距角控制模型，這樣不僅能使風電機組在故障后有效地恢復電壓和提高輸出電磁功率，而且在高風速階段還能使風電機組的輸入機械功率有效地降低。由于風能具有隨機變化特性，給風力發電系統的控制帶來了一定難度，尤其在高于額定風速階段的控制。因此出現了各種不同的槳距角控制策略，也形成了不同的控制優勢，總的來說針對不一樣的性能要求，需要采用不一樣的控制方案。

滑模變結構控制是非線性控制策略中的一種，和其他控制策略的不同之處在于控制系統結構的不固定性，表現在動態控制過程中，可以根據系統偏差有針對性的不斷變化結構，迫使被控制對象按照設計好的“滑動模態”軌跡運動，并且在設計滑模控制器時可以不用考慮被控對象參數及其擾動。雖然滑模變結構控制具有快速響應、對參數擾動不敏感、不用在線辨識、容易實現等優勢，但是當系統狀態軌跡到達滑模面后，難于保證沿滑模面無上下波動的向平衡點運動[7]。

鑒于此，本文在設計基于滑模控制算法的風力機槳距角控制器時，加入了兩個觀測器。其中一個用于估計風速波動信號的干擾；另一個用于觀測當風速波動時引起的風輪轉子轉速波動干擾。通過設計帶干擾觀測器的滑模控制器，使滑模切換項的增益降低，進而使風力機槳距角的滑模變結構控制抖振大大降低。然后利用Matlab/Simulink軟件進行仿真分析，證明了所設計控制器具有較好的魯棒性和穩定性。

1 風力機模型

由貝茲理論（Betz theory）可知[8]，風力機可以將空氣中的風能轉化為機械功率輸送到發電機，即

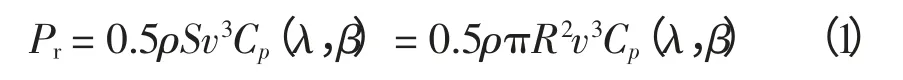
式中：Pr為風輪輸出的機械功率，W；ρ 為空氣密度，一般取1.25 kg/m3；S 為風力機葉片迎風掃略面積，m2；v 為風輪機上游風速，m/s；R 為風輪半徑，m；Cp為風能利用系數；β 風輪葉片槳距角，（°）；λ為葉尖速比，與槳距角和風輪轉速有關，即

式中：ωr為風輪旋轉角速度，rad/s。

關于風能利用系數Cp給出經驗公式[9]為

其中Λ 滿足：

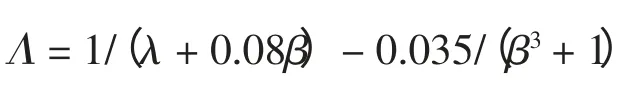
風力機的動態運動方程[10]為

式中：J 為風力機與發電機總的轉動慣量，kg·m2；Tr為風力機轉矩，N·m；Te為電機的電磁轉矩，N·m。因為本文主要研究如何優化槳距角控制器的控制效果，所以這里認為電磁轉矩Te是恒定的。

一般用液壓系統或電動轉置來執行變槳距動作指令，即變槳距執行機構[11]。為了方便控制算法公式的推導，將變槳執行機構數學模型等效為一階模型方程，即

式中：ε 為液壓伺服系統時間常數；βi為變槳距執行機構的輸入變量，（°）。

2 模型線性化

由于風輪的氣動轉矩是三個變量的非線性函數，即

將式（6）在風力機的恒功率運行工作點（vop，βop，ωr-op）泰勒展開，展開式為

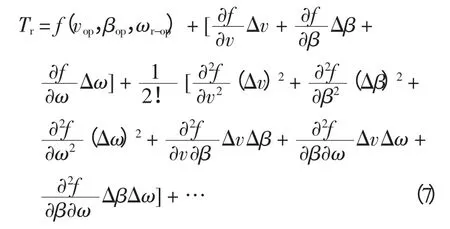
因為Δv = v - vop，Δβ = β - βop，Δω = ω - ωop，所以有

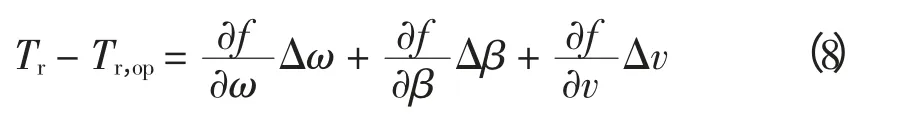
將展開式中的高階項忽略掉，并定義

則式（8）變為

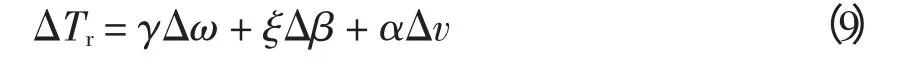
根據式（4）和式（9）以及關系式Tr=可推導出方程

恒功率工作點槳距角誤差變化率為

由式（11）可將式（10）進一步轉化為

設風力機參考變化轉速為Δωref，并令

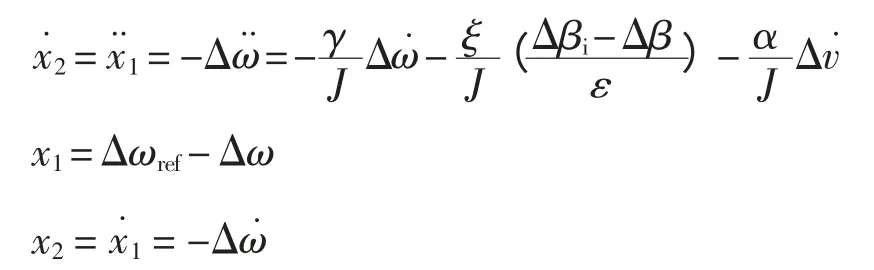
據此可將式（12）寫成矩陣形式為

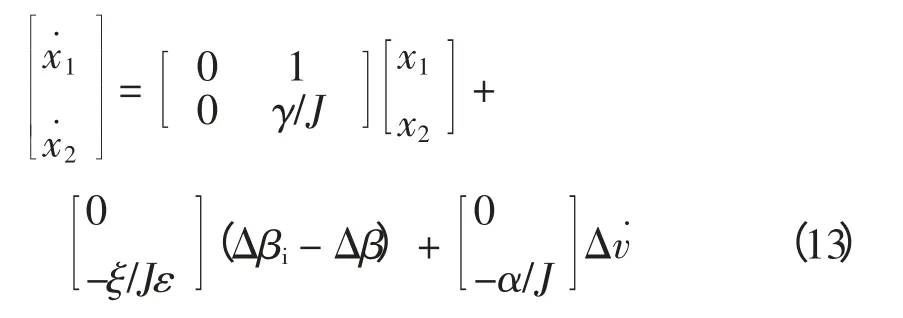
式（13）為下面控制器的設計提供了依據，其控制器的輸入量為Δω；控制器輸出量為u=Δβi-Δβ；干擾量為

3 設計控制器

3.1 常規滑模控制器的設計

常規滑模控制會把控制器設計為

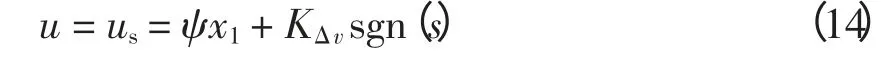
設切換函數為

式中：KΔv為干擾切換增益；c 為正的常數，且ψ 為轉速誤差變化的狀態系數，且有

對式（15）兩邊求導，可得

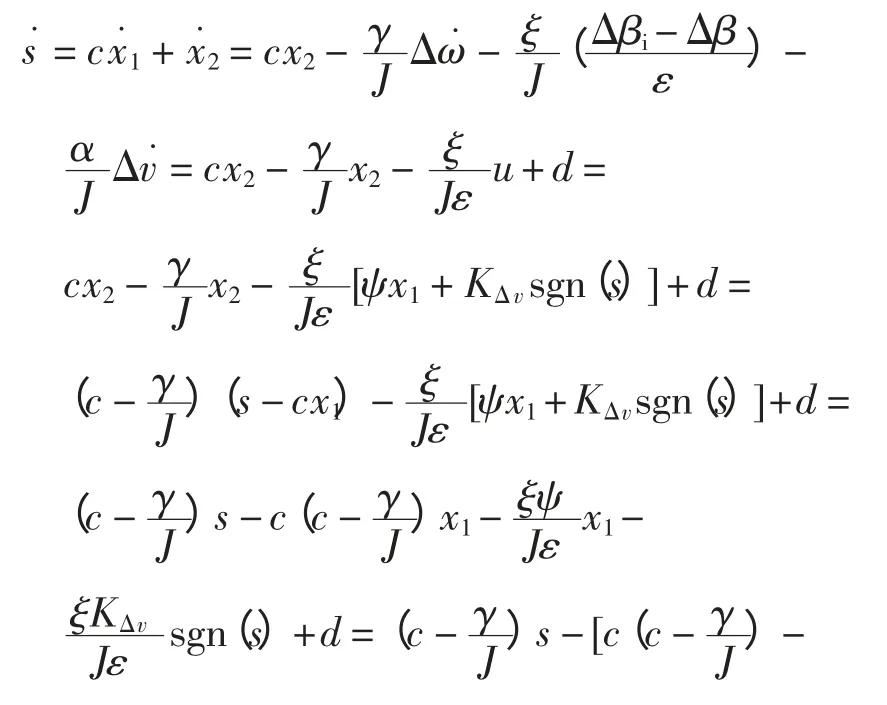
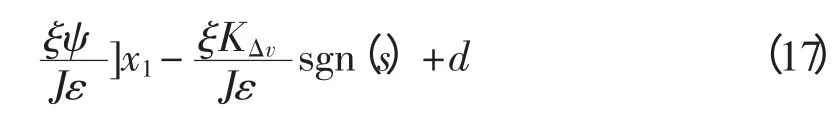
則有

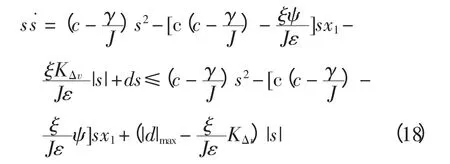
從式（16）可以看出，當系統干擾d 特別大時，KΔv也比較大，這樣就會是控制器在控制槳距角執行機構時產生抖振。

3.2 設計帶干擾觀測器的滑模控制器

為了能有效地觀測風力機的轉速變化和外部干擾變化，設計出干擾觀測器為

根據式（20）把滑模控制器設計成

式中：us=ψx1+KΔvsgn（s）；u0=，其帶干擾觀測器的控制框圖如圖1 所示。

分別建立Lyapunov 函數為

因此得出基于觀測器的滑模控制器的Lyapunov 函數為

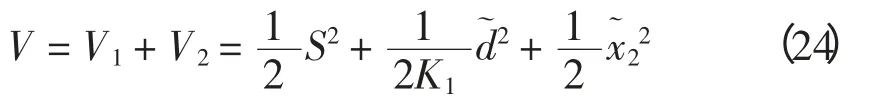
控制器中加入觀測器后，有

則有

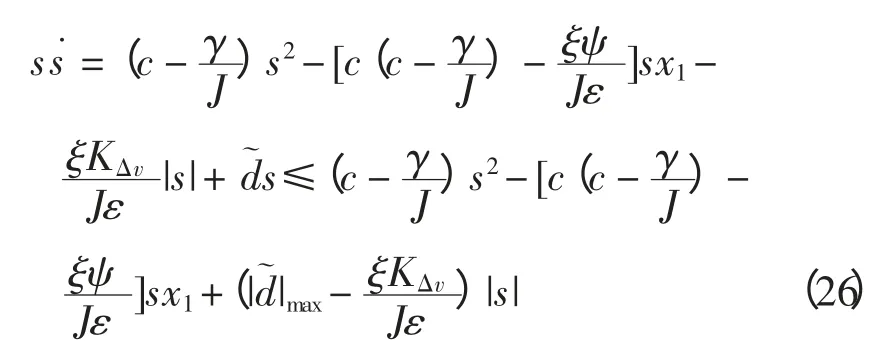
因此結合式（20），并假設干擾量為慢時變信號，即d˙=0，可以分別證明Lyapunov 函數V1和V2的穩定性。

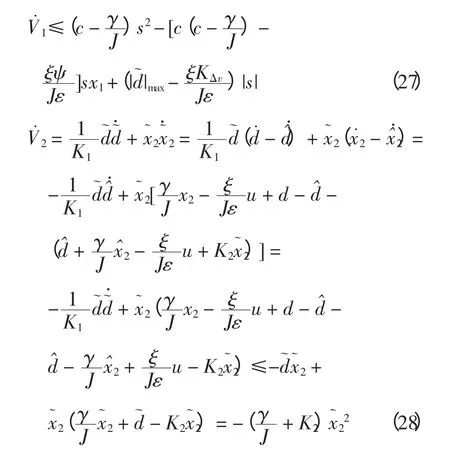
4 Matlab/Simulik 仿真分析

本文仿真采用的是額定功率為600 kW 的變槳距風電機組，主要參數為：風力機轉動慣量2.85×105kg·m2；發電機轉動慣量6.41×104kg·m2；額定風速11 m/s；風力機額定轉速為4.35 rad/s；變槳距執行機構中的電動機位移范圍0～30°，液壓伺服系統運行時間常數ε=0.05 s；采用的干擾觀測器狀態變量系數c=20，增益K1=15 000，K2=50。仿真結果如圖2～圖7 所示。

圖2 為隨機風速干擾信號，平均風速為v＞11 m/s，圖3 顯示了風力機槳距角在隨機風速干擾下的輸出信號曲線，圖4 和圖5 分別為傳統滑模控制算法和帶兩個觀測器的滑模控制算法下的槳距角的跟蹤曲線。

從圖2～圖5 可以看到，當風速高于額定風速時，風速的波動以及所引起的風力機轉子轉速波動，導致變槳距執行機構出現一定波動。從傳統滑模控制算法與本文提出控制算法的控制結果對比可以看出，在跟蹤槳距角變化曲線時傳統滑模控制出現了跟蹤信號抖振問題，但是通過設計的觀測器預先對干擾信號進行估計，可以使變槳距執行機構能很好地跟蹤槳距角變化曲線。

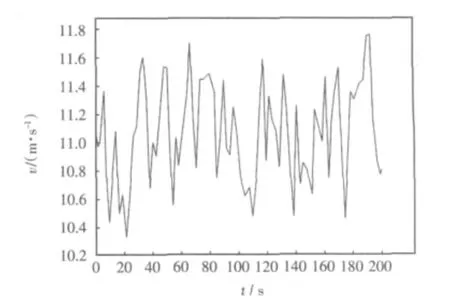
圖2 隨機風速信號曲線Fig.2 Curve of random wind speed signal

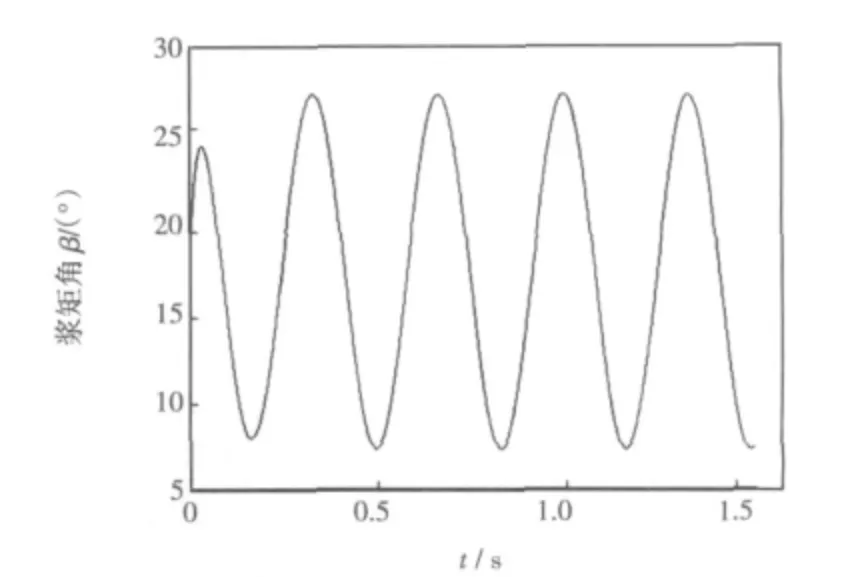
圖3 干擾情況下的槳距角變化響應曲線Fig.3 Response curve of pitch angle change under disturbance

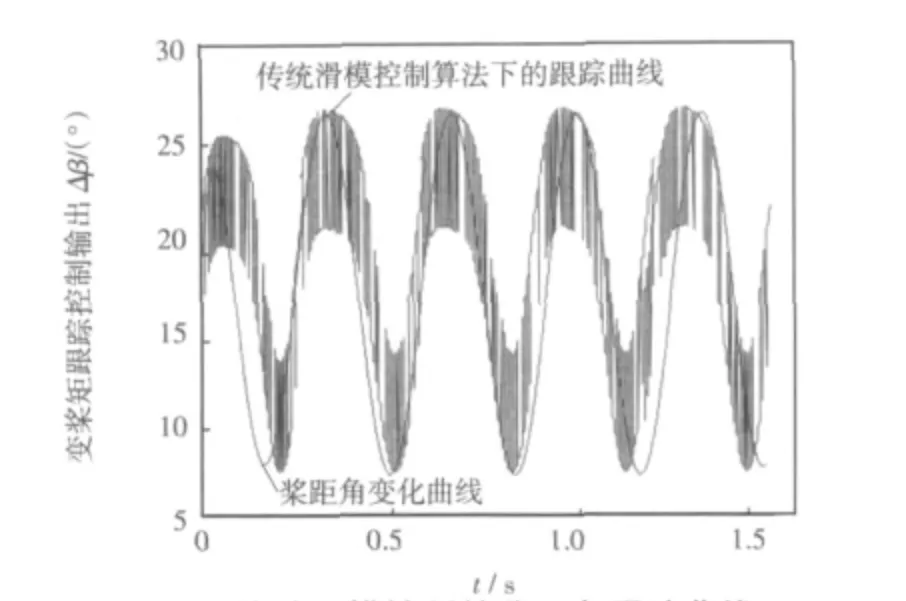
圖4 傳統滑模控制的槳距角跟蹤曲線Fig.4 Tracking curvs of pitch angle based on traditional sliding-mode control

圖5 基于觀測器的滑模控制的槳距角跟蹤曲線Fig.5 Tracking curvs of pitch angle based on slidingmode control with observer

從圖6 的轉速誤差曲線和圖7 的相軌跡可以看出，在滑模控制器中加入觀測器后，可以使控制系統誤差變化率逐漸減小，并且誤差能穩定在0附近。從而證明了所設計的控制器的有效性。

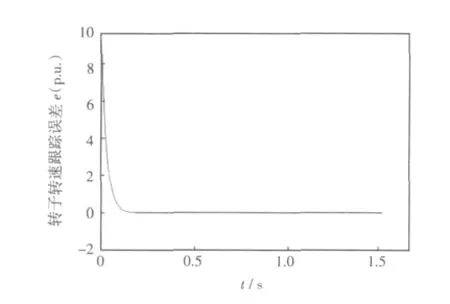
圖6 隨機風干擾下的轉速跟蹤誤差曲線Fig.6 Error curve of the tracking speed under the disturbance of random wind

圖7 轉速誤差及其變化率的相軌跡曲線Fig.7 Error of rotate speed and phase path curve of its change rate

5 結語

本文在設計基于滑模控制算法的風力機槳距角控制器時，加入了兩個觀測測器。其中一個用于估計風速波動信號的干擾；另一個用于觀測當風速波動時引起的風輪轉子轉速波動干擾。通過設計帶干擾觀測器的滑模控制器，使滑模切換項的增益降低，進而使風力機槳距角的滑模變結構控制抖振大大降低。最后通過Matlab/Simulink 軟件仿真，證明了所設計控制器具有較好的魯棒性和穩定性。

[1]王志新，張華強（Wang Zhixin，Zhang Huaqiang）.風力發電及其控制技術新進展（New development of wind energy generation and control strategy）[J]. 低壓電器（Low Votager），2009，10（19）：1-7，19.

[2]姚紅菊，趙斌（Yao Hongju，Zhao Bin）.變速恒頻風電機組額定風速以上恒功率控制（Constant power control of variable speed constant frequency wind turbine above rated wind speed）[J].能源與環境（Energy&Environment），2005（3）：12-13，49.

[3]Hansen A D，Soerensen P，Florin Iov，et al.Overall control strategy of variable speed doubly-fed induction generator wind turbine[C]// Wind Power Nordic Conference.Goteborg，Sweden：2004.

[4]Cardenas-Dobson R，Asher G M.Power limitation in variable speed wind turbines using pitch control and a mechanical torque observer[J].Wind Engineering，1996，20（6）：363-387.

[5]Slootweg J G，de Haan S W H，Polinder H，et al. Aggregated modeling of wind parks with variable speed wind turbines in power system dynamic simulations[C]//14th PSCC.Bologna，Italy：2002.

[6]遲永寧，關宏亮，王偉勝，等（Chi Yongning，Guan Hongliang，Wang Weisheng，et al）.SVC 與槳距角控制改善異步機風電場暫態電壓穩定性（Enhancement of transient voltage stability of induction generator based wind farm by SVC and pitch control）[J]. 電力系統自動化（Automation of Electric Power Systems），2007，31（3）：95-104.

[7]鄒賢求，吳政球，陳波，等（Zou Xianqiu，Wu Zhengqiu，Chen Bo，et al）. 變速恒頻雙饋風電機組頻率控制策略的改進（Improved frequency control strategy for variablespeed constant-frequency doubly-fed induction generator wind turbines）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2011，23（3）：63-68.

[8]劉金琨，孫富春（Liu Jinkun，Sun Fuchun）.滑模變結構控制理論及其算法研究與進展（Research and development on theory and algorithms of sliding mode control）[J].控制理論與應用（Control Theory & Applications），2007，24（3）：407-418.

[9]Orabi Mohamed，Ahmed Tarek，Nakaoka Mutsuo，et al.Efficient performances of induction generator for wind energy utilization [C]//The 30th Annual Conference of IEEE Industrial Electronics Society.Busan，Korea：2004.

[10]Slootweg J G，Polinder H，Kling W L.Dynamic modeling of a wind turbine with doubly fed induction generator[C]//Power Engineering Society Summer Meeting. Vancouver，Canada：2001.

[11]夏長亮，宋戰峰（Xia Changliang，Song Zhanfeng）.變速恒頻風力發電系統變槳距自抗擾控制（Pitch control of variable speed constant frequency wind turbines based on active-disturbance-rejection controller）[J].中國電機工程學報（Proceedings of the CSEE），2007，27（14）：91-95.

[12]劉欣然（Liu Xinran）.模糊滑模控制及其在風力發電系統中的應用研究（Research on Fuzzy Sliding Mode Control and Its Applications in Wind Turbine System）[D].北京：華北電力大學控制與計算機工程學院（Beijing：School of Control & Computer Engineering of North China Electric Power University），2008.