面向等幾何分析的B樣條參數體生成方法

許華強， 徐 崗， 胡維華， 汪國昭

（1. 杭州電子科技大學計算機學院圖形圖像研究所，浙江 杭州 310018；2. 浙江大學數學系圖像圖形研究所，浙江 杭州 310027）

隨著CAD/CAE 領域的快速發展和降低設計成本的需要，設計與分析的一體化已成為大勢所趨[1]。目前，有限元分析已經成為CAE 領域對CAD 產品進行仿真模擬的主流方法。然而，當今設計與模擬分析階段幾何數據模型的不一致性，嚴重影響了求解精度和計算效率。據統計，數據交換可以占到CAE 軟件大約70%的運行時間，而整個CAD/CAE 過程80%左右的工作量用于離散網格生成階段。此外，由于有限元分析中的計算域只是對CAD模型的逼近表示，這必然導致模擬分析及優化結果存在一定的誤差。對于某些模擬仿真中的物理問題而言，由此所導致的誤差可能會非常顯著，因此，如何實現真正意義上的CAD/CAE 系統的無縫融合，便成為CAD/CAE 向前發展過程中亟需解決的問題。

等幾何分析方法的提出為實現CAD/CAE系統的無縫融合提供了新途徑[2]。相對于經典的有限元分析方法，該方法的主要優勢在于：

1）具有與CAD階段統一的幾何數學模型，或者兩個階段的幾何數學模型具有互用性，無需進行容錯轉換；

2）采用高階基函數作為形函數，具有良好的收斂性；

3）求解所得到的物理場具有高階連續性，對某些薄殼問題的求解可達到比較高的精度；

4）實現了CAD 模型與計算域的精確轉換，提高了模擬分析及優化設計的準確度；

5）在細化過程中（節點插入或升階操作）可以使計算域的幾何保持不變[3]，這一特性適用于流體和固體的耦合問題。等幾何分析方法的提出為已趨成熟的幾何造型領域注入了新的活力，目前已成為幾何設計與計算領域新的關注熱點，由于等幾何樣條分析的研究目前處于起步階段，該方法在應用的廣度與模擬的自適應性等方面仍存在一定的局限性。

等幾何分析方法雖然無須由CAD 模型的邊界曲面表示生成離散的四面體網格作為計算域，但仍然需要由其邊界表示生成連續的參數樣條體表示以完成計算域的構造。這一體參數化過程與有限元方法中的網格生成過程的不同之處在于：我們需要在精確保持邊界曲面的前提下，將CAD 模型的內部用若干個三變量參數體填充起來，而有限元分析中的網格生成過程得到的則是該CAD模型的四面體網格逼近表示。CAD 模型的體參數化結果對模擬分析的精度有著重要影響[4]，這一問題在Cottrell 和 Hughes 等所著的《Isogeometric Analysis: Toward Integration of CAD and FEA》一書中被列為等幾何分析面臨的最富有挑戰性的公開問題之一。目前，國際上對這一問題的研究屈指可數。Martin 等利用離散調和函數方法來完成對四面體網格的參數體逼近[5]；Escobar 等利用參數域剖分和插值逼近技術來構造三角網格模型的三變量T 樣條體參數化[6]；Zhang 等利用參數映射和八叉樹技術來構造三角網格模型的三變量T樣條體參數化[7]。上述3種方法雖然均可有效生成體參數化，但它們的缺點是顯而易見的，即其輸入是三角網格模型或者四面體網格模型，而參數樣條表示是CAD系統中的標準形式，顯然違背了等幾何分析方法的精髓——精確幾何表示。理想的方法應該是以CAD 模型的邊界樣條曲面表示作為輸入，構造其內部空間的參數體表示。本文提出了基于模板的由邊界曲面生成參數體的新方法。首先給出了插值邊界曲面的Coons體的參數表達式。由該表達式的離散表示，內部控制頂點可表為邊界控制頂點的線性組合。然后由其離散表示可得到Coons模板，并將Coons模板推廣到統一形式，這為內部控制頂點的生成提供了更多選擇。本文通過幾個熱傳導問題的例子對由不同的模版所得到的不同的體參數化結果及其對等幾何分析結果的影響進行了比較分析。

1 Coons 參數體

給定6張邊界曲面S(0,v,w),S(1,v,w) ,S(u,0,w),S(u, 1,w),S(u,v, 0),S(u,v, 1), 插值上述6張曲面的Coons參數體S(u,v,w)可按如下方式構造：

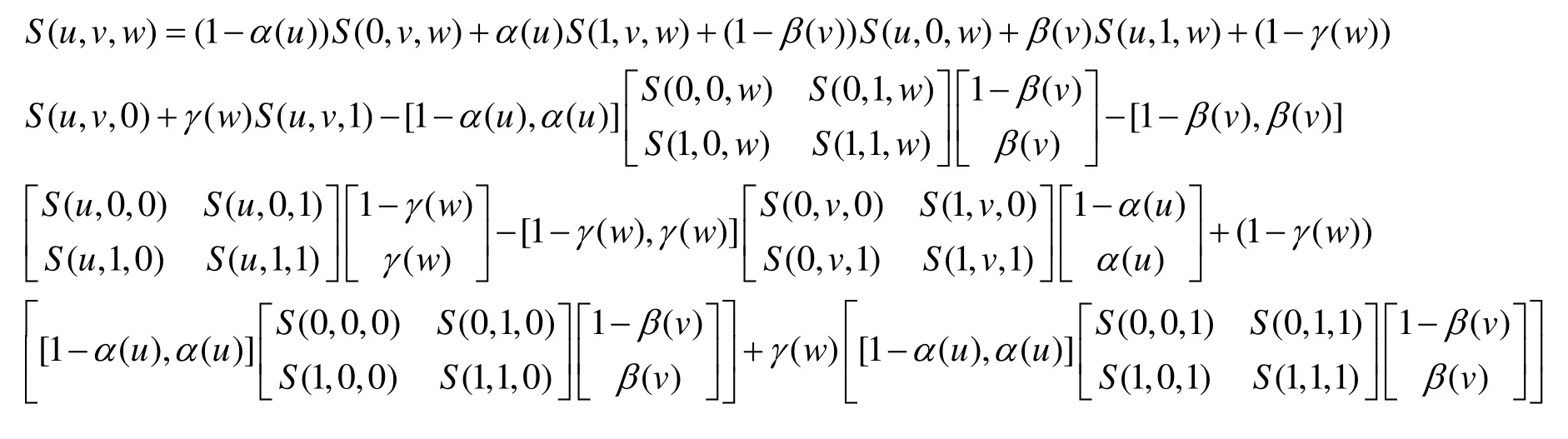
圖1 Coons參數體

其中，α(u)β(v)γ(w)為滿足如下條件的參數函數：

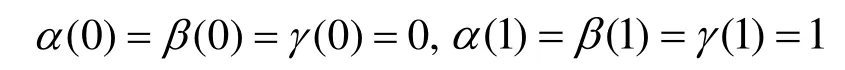
通過直接計算可證明參數體S(u,v,w)插值6張邊界參數曲面，它可以看作插值4條邊界曲線的Coons曲面的推廣。圖1給出了一個Coons參數體S(u,v,w)的例子。

若給定的邊界曲面為B樣條曲面，并且相對的B樣條曲面具有相同的次數、控制頂點數目和節點向量，α(u)β(v)γ(w)為參數多項式函數，則按照Coons 參數體的定義所生成的參數體仍為B樣條形式。若α(u) =u,β(v)=v，γ(w) =w,并且邊界控制頂點按圖2給出，則每一個控制頂點Pi,j,k可賦予一組參數值(u,v,w) =(i/l,j/m,k/n)， 內部的控制頂點Pi,j,k可按照如下的離散形式構造：

則相應的B樣條參數體可記為

其中，Ni(u),Nj(v),Nk(w)為B樣條基函數，其節點向量由邊界B樣條曲面給出。

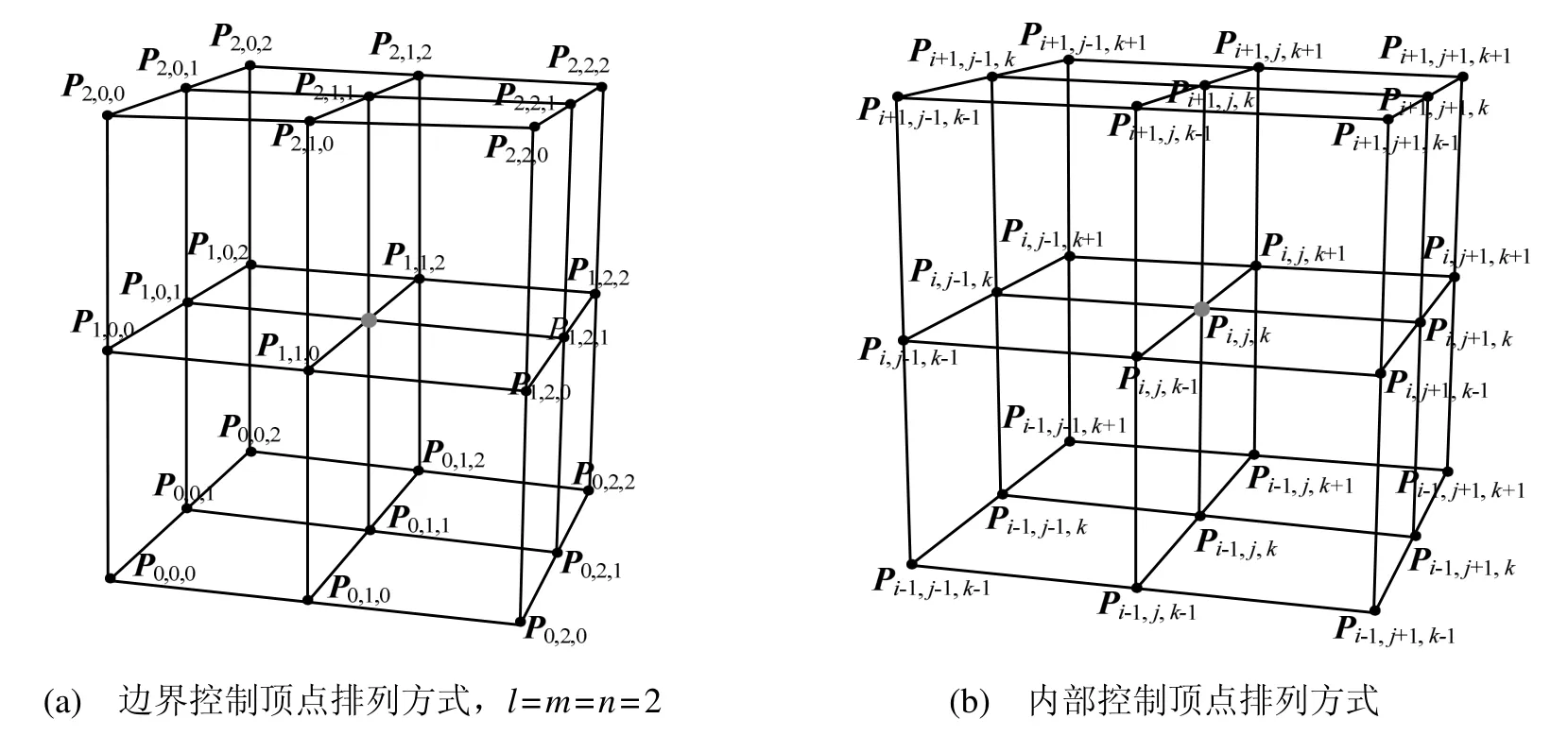
圖2 排列方式

2 B樣條參數體生成的模板方法

本文所提出的模板實際上表達了每一個內部控制頂點與其相鄰控制頂點的線性關系。對B樣條Coons體的每一個內部控制頂點Pi,j,k來說，其與相鄰控制頂點之間的關系可表示為

上述關系可以表示為圖3(a)中簡潔的模板表示。對一個具有(l-1)× (m-1)× (n-1)個內部控制頂點的B樣條參數體來說，我們將得到(l- 1)× (m-1)× (n -1 )個線性方程。其所組成的線性系統的系數矩陣為一稀疏矩陣。在B樣條體的內部，其表現為內部待求控制頂點之間的關系，而在其邊界，則表現為邊界已知控制頂點與內部待求控制頂點之間的關系。

等式(2)所表示的離散Coons模板可以擴展到如下形式：

上述關系可以表示為圖3(b)中簡潔的模板表示。該模板表示方法提供了3個參數α,,βγ，增加了B樣條參數體生成的自由度。為使內部待求的控制頂點位于邊界已知的控制頂點所組成的凸包內，參數α,,βγ應滿足如下約束條件

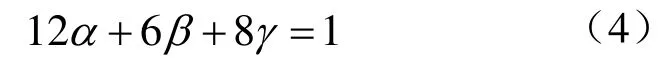
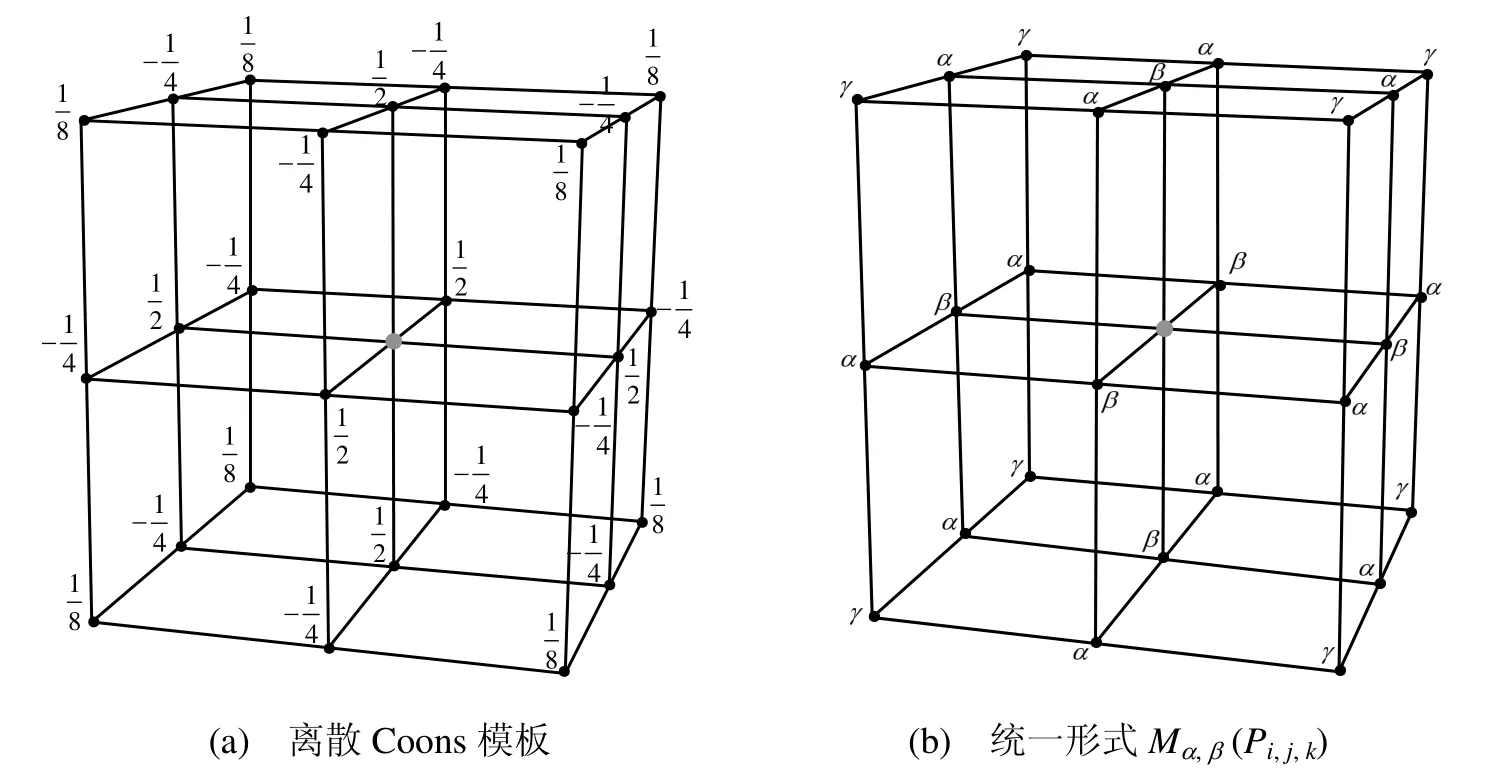
圖3 模板表示方法

該模板表示形式可以記為Mα,β(Pi,j,k)。對于給定的邊界B樣條曲面，用戶可選擇不同的參數α,β來構造B樣條參數體，γ可根據α,β的值由式（4）求出。例如，離散Coons模板可記為其中離散Laplacian 模板可記為，其中離散調和模板可記為其中

圖4給出了在邊界B樣條曲面相同的情形下，依據上述3種不同的模板方法所生成的B樣條參數體的例子。為將3種模板進行比較，本文給出了所生成的B樣條參數體的等參數曲面分布，可以發現離散調和模板所生成的B樣條參數體的等參數曲面分布最為均勻。另外，本文將生成的體參數化結果在三維等幾何分析中進行了測試。所求解的物理仿真問題為如下的三維熱傳導問題：

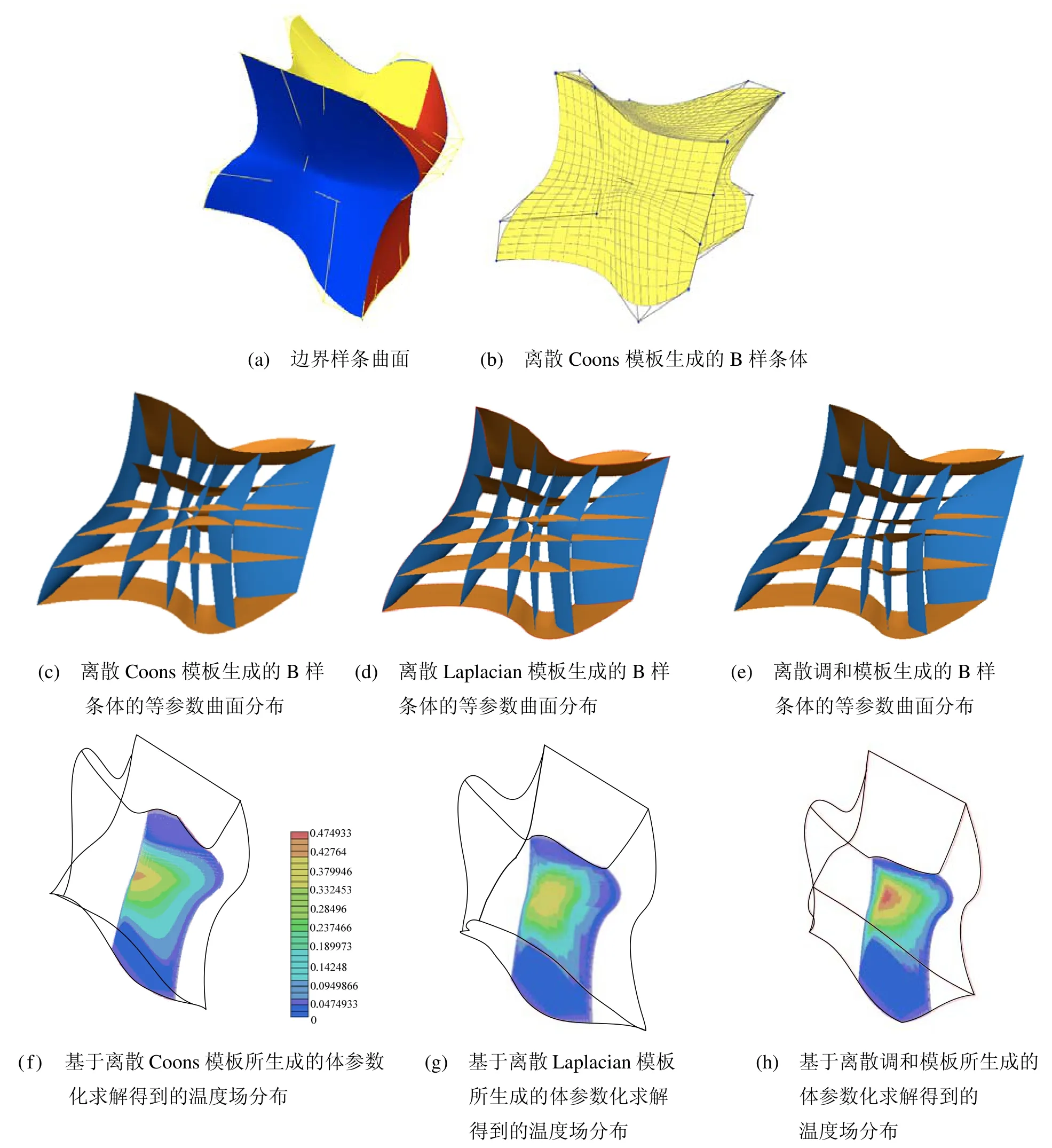
圖4 體參數化實例

3 結 論

三維等幾何分析中的計算域通常表示為參數樣條體。本文提出了一種由邊界曲面生成參數體的模板方法。首先給出了插值邊界參數曲面的Coons體的參數表達式。由其離散表示可得到Coons模板，并將Coons模板推廣到統一形式，這為內部控制頂點的生成提供了更多自由度。通過模板方法，內部控制頂點可通過求解一個稀疏線性系統得到。本文通過熱傳導問題的實例對由不同的模板所得到的體參數化結果及其對等幾何分析的影響進行了比較分析。

[1]高曙明, 何發智. 異構CAD系統集成技術綜述[J]. 計算機輔助設計與圖形學學報, 2009, 21(5): 561-568.

[2]Hughes T J R, Cottrell J A, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement [J]. Computer Methods in Applied Mechanics and Engineering, 2005,194(39-41): 4135-4195.

[3]徐 崗, 王毅剛, 胡維華. 等幾何分析中的r-p型細化方法[J]. 計算機輔助設計與圖形學學報, 2011,(12): 2019-2024.

[4]Xu Gang, Mourrain B, Duvigneau R, et al.Parameterization of computational domain in isogeometric analysis: methods and comparison [J].Computer Methods in Applied Mechanics and Engineering, 2011, 200(23-24): 2021-2031.

[5]Martin T, Cohen E, Kirby R M. Volumetric parameterization and trivariate B-spline fitting using harmonic functions [J]. Computer Aided Geometric Design, 2009, 26(6): 648-664.

[6]Escobar J M, Cascon J M, Rodr?guez E, et al. A new approach to solid modeling with trivariate T-splines based on mesh optimization [J]. Computer Methods in Applied Mechanics and Engineering, 2000, (45-46);2011, 3210-3222.

[7]Zhang Y, Wang W, Hughes T J R. Solid T-spline Construction from boundary representations for genus-zero geometry [J]. Computer Methods in Applied Mechanics and Engineering, 2012,(249-252):185-197.