2D圖形引擎中的平面多邊形內外點判別

楊玉婷， 康厚良

（云南大學旅游文化學院，云南 麗江 674100）

在2D圖形引擎中，可見性判定的主要目的是對于給定的場景和觀察視點，通過對遮擋關系進行快速判斷，丟棄大量不需要繪制的圖形對象，從而降低場景的復雜程度，增加整個場景的真實感，最終實現低負荷繪制和網絡傳輸[1-3]，因此，是一個非常重要的問題。另外，不論是2D對象，還是3D對象最終都將被渲染到顯示屏上，由于顯示屏的大小是固定的，因此，不是場景中的所有可見部分都可以在顯示屏中顯示出來，需要根據顯示屏的尺寸對場景中的可見部分進行裁剪，即屏幕裁剪[4]，如圖1所示。通過圖像流水線處理后的可見部分可能是一個或若干個多邊形，所以在屏幕裁剪過程中，一般是先找出多邊形和屏幕邊界的交點，然后通過連接各邊界點從而確定屏幕中的可見部分[5]。在一些特殊情況下，屏幕可能部分甚至全部位于待判定多邊形內，此時則需要對屏幕各頂點與待判定多邊形的內外關系進行判斷，因此點與多邊形內外關系的判斷在2D圖形引擎中很重要。

圖1 屏幕裁剪

點與多邊形內外關系的判斷算法很多，常見算法包括射線法[6]、叉積判斷法[7]、多邊形方向法[8]、基于端點和交點編碼法[9]、鏈碼表及多邊形特征形法[10]，以及基于單調性的相關邊法[11]等等。結合2D圖形引擎的特點和流行的內外點判別算法給出了在DirectX平臺上使用VC++實現的平面多邊形內外點判斷算法，并將其應用于實際的2D圖形引擎中。通過具體實例證明，該算法能實時的對點和多邊形的內外關系進行較好的處理，并將裁剪后的多邊形渲染到屏幕上。

1 算法的數據結構

在計算機圖形學中提及的多邊形一般多指簡單多邊形，并且規定多邊形沿逆時針方向時為正，沿順時針方向時為負。

為了方便多邊形內外點判斷算法的實現，首先設計適當的數據結構存儲多邊形頂點，并要求能滿足頂點的排序、增加和刪除等操作需要。因此，使用靜態數組存儲原始多邊形（未進行任何處理的多邊形）序列，而操作時使用靜態鏈表存儲。數組/鏈表以頂點為單位存儲多邊形的所有頂點信息，并規定如下：

（1）每一個存儲單元對應多邊形的一個頂點。

（2）每兩個相鄰元素的一個組合對應于多邊形的一條邊。

（3）有一個共同元素的一對組合對應于多邊形的兩條相鄰邊，其中公共元素即為兩條相鄰邊的相交頂點。

因此，多邊形單個頂點的數據結構和多邊形頂點數組定義如下：

typedef struct VERTEX2DI_TYP

{

int X,Y; // the vertex

} VERTEX2D, *VERTEX2D_PTR;

因此，如圖2所示的多邊形P0P1P2… P7表示為：

VERTEX2DI_PTR v2d=new VERTEX2DI[n]; //n=8

VERTEX2D_PTR pv2d=v2d; //指向多邊形序列的指針

VERTEX2D_PTR pt; //多邊形的特征值列表

int *c, *s; // 多邊形的垂直鏈碼表和水平鏈碼表

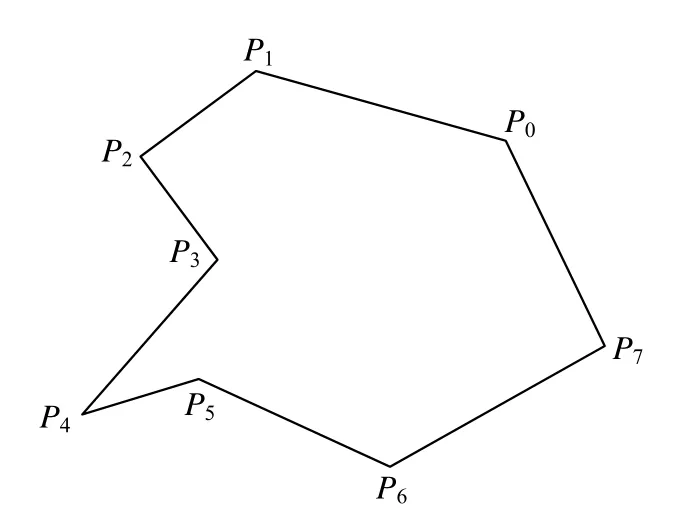
圖2 任意多邊形

另外，定義多邊形頂點的齊次坐標結構和多邊形表示如下：

typedef struct VERTEX3D_TYP

{

int X,Y; // 頂點坐標

int Z; // 方向向量

} VERTEX3D, *VERTEX3D_PTR;

VERTEX3D v3d[8]= {P0, P1, P2, P3, P4, P5, P6, P7};

VERTEX3D_PTR *pv3d=v3d;//指向多邊形序列的指針

VERTEX3D most[len]; // 存儲多邊形沿x方向和y方向的最大值和最小值，其中len=4

此時，多邊形頂點Pi(i∈[0,∞))的齊次坐標表示為(Xi,Yi,Zi)，其中Zi表示方向向量，且值恒等于1，即Pi=(Xi,Yi,1)

2 算法描述

算法的基本思想是：首先，以待測點作為原點建立直角坐標系，生成多邊形的水平鏈碼表和垂直鏈碼表；然后，刪除與判斷點和多邊形無關的冗余邊/冗余點，獲得多邊形的特征形。接著，判斷待測點與特征形的內外關系；最后，確定待測點與平面多邊形的內外關系。算法步驟的具體描述如下：

Step 1對多邊形頂點序列進行逆時針排序。排序方法是：將多邊形的n個頂點分別用Pi(i∈[0,n))表示，通過比較線段OPi（過坐標原點和多邊形頂點Pi(i∈[0,n))的線段）與x正半軸組成的夾角的大小，確定多邊形各個頂點逆時針排序時的先后關系，如圖3所示。具體操作包括以下4個方向：

圖3 多邊形的逆時針排序

1）根據頂點個數n創建臨時數組jiaodu[n],用于存儲OPi與x正半軸組成的夾角的大小；

2）計算OPi與Ox的正弦值，若Pi.y＞ 0，

表1 temp在不同象限對應的角度值

4）對數組jiaodu[n]及與之對應的多邊形頂點序列v2d進行逆時針排序

Step 2以待測點P為原點建立新的直角坐標系，具體操作包括以下2個方面：

1）根據待測點P，計算新坐標系的平移量dx=p.x，dy=p.y，因此平移矩陣

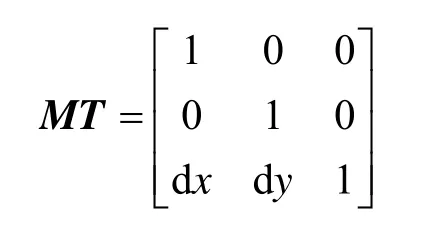
2）計算多邊形的頂點Pi(i∈[0,n))在新坐標系x′oy′中的坐標值Pi′，即Pi′=Pi*MT，效果如圖3所示。

Step 3根據Pi′ (i∈[0,n))的位置標記多邊形頂點的水平鏈碼值(HorizValue)和垂直鏈碼值(VertiValue)。標記規則為：在垂直方向上編碼時，對 點Pi′(i∈[0,n))，若 縱 坐 標yi′＞0，則VertiValue=1，否則，VertiValue=0；在水平方向上編碼時，對點Pi′(i∈[0,n))，若橫坐標xi′＞0，則HorizeValue=1，否則，HorizeValue=0[6]；最后，將計算結果分別存儲在數組c和s中，且數組長度均為n。由此，圖4中多邊形的垂直編碼表和水平編碼表分別為11100000和10000001，且n=8。

Step 4刪除多邊形中與待測點無關的冗余邊或冗余點，獲得多邊形的特征形。具體操作包括以下3個方面：

1）對垂直鏈碼表進行連續的0（1）檢測，方法是：檢測垂直鏈碼表c中是否存在連續的3個或3個以上的0或1，若有，則用第一個及最末一個0或1來代替這段連續的0（1）序列，并獲得簡化后的垂直鏈碼表c_new；

2）據c_new計算相應的水平鏈碼表s_new和多邊形頂點數組v2d_new，頂點數n遞減；

3）對水平鏈碼表s_new重復執行步驟1)和2)的操作。

簡化后的多邊形的垂直鏈碼表和水平鏈碼表為：1100和1001，對應特征形的頂點序列為P0(10,4)，P2(-28,2)，P3(-20,-10)，P7(20,-20)，且n=4，如圖4所示。

圖4 多邊形的垂直鏈碼、水平鏈碼和特征形

Step 5判斷點與多邊形的內外關系

1）當n=2時，多邊形簡化為線段，則只需線段是否過原點，若過原點，則待測點在多邊形內；否則，點在多邊形外。

2）當n≥3時，遍歷特征形頂點序列查找沿x，y方向的最大值和最小值并存入數組most中，數組most的長度len∈[3,4]，如果most中存在相同的頂點坐標（多邊形發生了退化現象[4]），則刪除相同頂點，len值遞減，并對most進行逆時針排序。

3）當len＞2時，取most序列中的前3個點分別賦給q0，q1，q2，定義矢量z={0,0,1}，如果(q0q1×q1q2)·z＞0，則多邊形特征形的方向為正，否則為負。

4）當len=2時，設剩余兩點分別為Pi，Pj，如果（Pi-1Pi×PiPi+1)·z＞0，則多邊形特征形的方向為正，否則為負。

5）據特征形的方向性判斷點與多邊形的內外關系，即連接待測點P與多邊形的任意兩個相鄰頂點，獲得三角形△PPiPi+1，執行Step 3，計算三角形的方向，如果三角形的方向與特征形方向相同，則待測點P位于多邊形內，否則位于多邊形外。如圖5所示，△PP3P7與多邊形特征形P0P2P3P7方向相同，因此待測點P位于多邊形內。

圖5 特征形的方向性及△PPiPi+1的方向性

3 復雜性分析

設多邊形頂點數為n，多邊形的特征形的邊數為m，待測點為P。首先，計算多邊形的水平鏈碼表和垂直鏈碼表的時間復雜度均為O(2*n)；然后，分別對多邊形Verti和Horize進行去0和去1運算，求得時間復雜度為O(4*n)；接著，計算待測點與特征形內外關系的時間復雜度，當m=2時為O(1)，m≥3時為所以時間復雜度的范圍為最后，計算待測點與平面多邊形的內外關系的時間復雜度為O(1)；因此，整個算法的時間復雜度范圍為由此可知，算法的整體時間復雜度是線性的。

4 實驗結果及分析

在所設計的2D線框引擎中，當多邊形與屏幕邊緣相交時，首先對多邊形進行屏幕裁剪，獲得頂點的渲染序列；然后判定屏幕頂點與多邊形的內外關系，屏幕頂點位于多邊形內，則作為新的渲染頂點被加入到渲染序列中，否則保持裁剪后的渲染序列不變；最后，對渲染序列進行排序，并根據頂點渲染序列將多邊形渲染到屏幕上。

相應的測試內容包括：

1）當多邊形完全位于屏幕內時的變化；

2）多邊形部分位于屏幕內時的變化；

3）多邊形發生動態變化（移動、旋轉）時，屏幕頂點與多邊形的關系。計算機硬件環境為：Duo T6400 2GHz*2，內存為2GHz，軟件環境為：Visual Studio 2005和DirectX，測試效果如圖6所示。

圖6 多邊形與屏幕頂點關系判定的測試

另外，以多邊形邊數分別為4,6,8,12,16,32隨機生成的任意多邊形為基礎，判斷1000,000個隨機點與多邊形的內外關系，測試算法效率。由于程序運行時間可能會受到外界的干擾，因此對每個多邊形都進行了多次測試并取平均值作為最終結果，其中時間的單位由CPU滴答轉換為秒，并與文獻[8]比較，測試結果如表2所示。

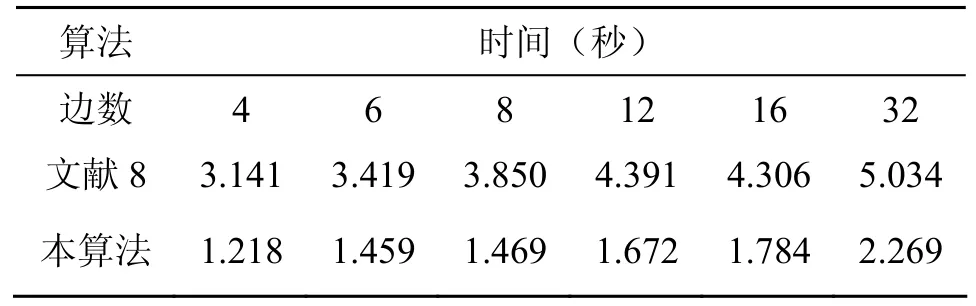
表2 兩種算法的耗時比較

從運行效果可以發現，隨著處理的多邊形邊數的增加，本算法在判斷速度上的優勢更加明顯，證明其具有較好的實際應用價值，并且也非常簡單易行。

[1]Cohen D, Chrysanthou Y, Silva C, et al. A survey of visibility for walkthrough applications [J]. IEEE Transactions on Visualization and Computer Graphics,2003, 9(3): 412-431.

[2]普建濤, 查紅彬. 大規模復雜場景的可見性問題研究[J]. 計算機研究與發展, 2005, 42(2): 236-246.

[3]楊玉婷, 康厚良. 大規模室內場景中的入口技術[J].重慶理工大學學報（自然科學版）, 2011, 25(11):78-85.

[4][美]Andre LaMothe著. “3D游戲編程大師技巧”[M].李祥瑞, 陳武譯, 北京: 人民郵電出版社, 2005.

[5]林 芳, 康寶生. 平面多邊形裁剪算法評述[J]. 西安建筑科技大學學報(自然科學版), 2003, 35(3):95-98.

[6]Taloy G. Point in polygon test [J]. Survey Review,1994, 32(254): 479-484.

[7]孫家廣. 計算機圖形學(第3版)[M]. 北京: 清華大學出版社, 2000: 414-418.

[8]李維詩, 李江雄, 柯映林. 平面多邊形方向及內外點判斷的新方法[J]. 計算機輔助設計與圖形學學報,2000, 12(6): 405-407.

[9]彭 歡, 陸國棟, 譚建榮. 基于端點與交點編碼的矩形窗口多邊形裁剪新算法[J]. 工程圖學學報,2006, 27(4): 72-76.

[10]周 欣, 張樹有, 潘志庚. 基于鏈碼和特征形的多邊形內外點判斷算法[J]. 計算機輔助設計與圖形學學報, 2006, 18(9): 1317-1321.

[11]李基拓, 陸國棟, 馮 星. 基于單調性與相關邊的多邊形內外點判斷算法[J]. 中國圖象圖形學報(A),2002,7(6): 596-600.