潛地導彈出筒運動仿真

陳志剛，齊 強，周 源

（海軍航空工程學院a.研究生管理大隊；b.7系，山東煙臺264001）

潛地導彈一般采用垂直發射的方式，導彈直接在潛艇的垂直發射筒內貯存并實施發射。導彈在發射筒中的運動是潛地導彈垂直水下發射的初始階段，是影響導彈水中運動的非常重要的因素，直接影響潛地導彈的水下發射可靠性。導彈的出筒運動不僅與導彈本身的結構參數有關，還受到潛艇運動等外界因素的影響[1-2]。文中假設導彈是剛體，通過分析導彈的受力環境，建立了潛地導彈出筒運動模型并進行數值計算，研究了導彈出筒運動各參數的變化以及潛艇搖擺運動對導彈出筒速度和出筒姿態的影響。

根據導彈與發射筒之間的適配器數量不同，將導彈出筒運動分為2段[3]：第1段指導彈與發射筒之間有多圈適配器相支撐，忽略導彈與發射筒之間的徑向相對運動，而只考慮軸向相對運動；第2段指導彈與發射筒之間只有一圈適配器相支撐，既考慮導彈與發射筒之間的軸向相對運動，又考慮導彈與發射筒之間的徑向相對運動，且導彈相對發射筒有相對角運動。

1 導彈出筒運動模型

為了研究導彈在發射筒內的運動特性，建立發射坐標系、彈體坐標系、艇體坐標系和速度坐標系。導彈出筒運動的動力學模型[3-6]如下：

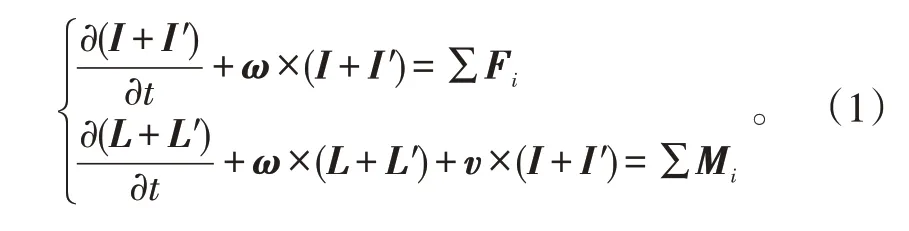
式（1）中：I和I′分別表示導彈和導彈周圍流體的動量矢量；L和L′分別表示導彈和導彈周圍流體的動量矩矢量；ω表示導彈的角速度矢量；v表示導彈的速度矢量；∑Fi表示導彈所受到的外力矢量和；∑Mi表示導彈所受到的外力矩矢量和。

2 導彈的受力分析與模型的簡化

2.1 導彈在出筒運動中的受力分析

1）導彈在流體中運動時受到流體動力和流體動力矩的作用，其大小取決于流體介質的性質、導彈外形和導彈的運動狀態[7-8]。將流體動力和流體動力矩分解到彈體坐標系，有：

式（2）中：Cx1、Cy1和Cz1表示流體動力因數；mx1、my1和mz1表示流體動力矩因數；q表示流體動壓力；S表示導彈的最大橫截面積；L表示導彈的長度。

2）導彈的重力為

重力的作用中心在導彈的質心，對導彈不產生力矩作用。

3）導彈在出筒過程中受到海水靜壓力的大小為

式（4）中：p0表示大氣壓力；H表示導彈頭部到海面的深度。海水靜壓力作用在導彈的頭部，當靜壓力作用線不通過導彈質心時就會對導彈產生力矩MP。

4）導彈出筒運動的動力是發射筒底部的工質氣體對導彈的推力，其大小F取決于發射動力系統的性能。文中假設推力為常數。工質氣體的推力作用于導彈的尾部，當推力作用線不通過導彈質心時，就會對導彈產生推力力矩MF。

5）導彈在發射筒內做垂向運動，導彈外側的適配器和氣密環與發射筒內壁之間產生摩擦，摩擦力方向與推力方向相反。文中假設摩擦力大小Fm為常數[9]。當摩擦力作用線不通過導彈質心時，就會對導彈產生摩擦力力矩MFm。

6）在導彈發射的第2 段過程中，由于導彈發生相對發射筒的姿態變化，適配器受到壓縮，因而導彈會受到適配器約束反力和約束反力矩的作用。以俯仰平面為例（見圖1），約束反力和反力矩的大小為：

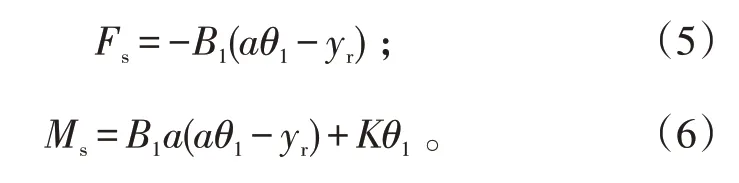
式（5）、（6）中：B1表示適配器的抗壓剛度；K表示適配器的抗彎剛度；θ1表示導彈相對艇體坐標系的俯仰角；yr表示導彈在俯仰平面沿oy1軸的平移。

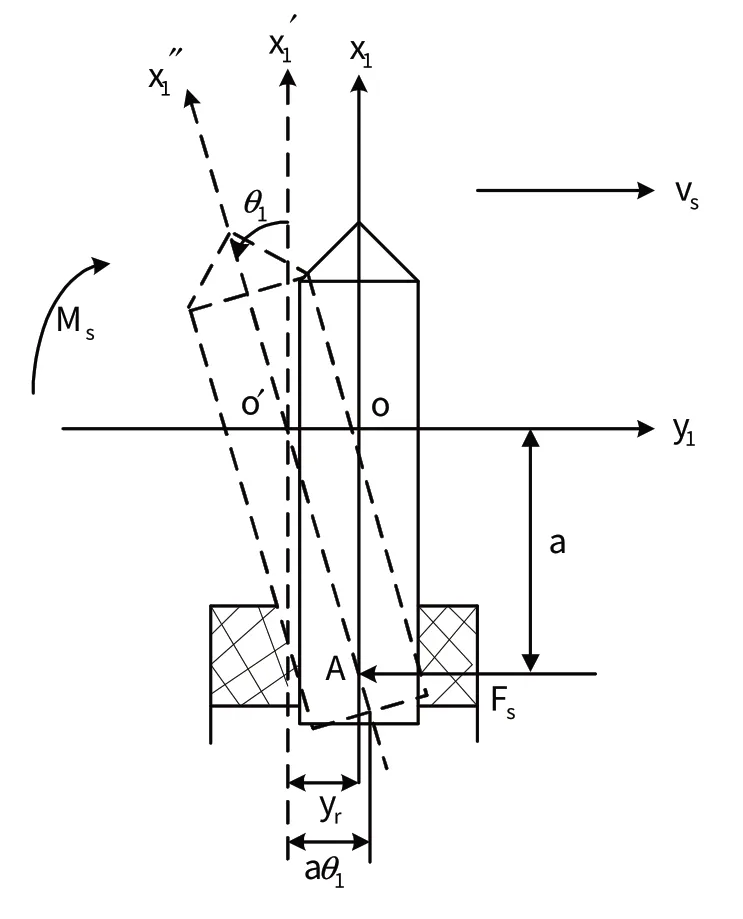
圖1 約束反力和反力矩示意圖

2.2 潛艇運動的簡化模型

潛艇在水下的運動是六自由度的運動，并在海底洋流等因素的影響下做不規律的變化。文中在計算時不考慮潛艇在3 個軸方向上的震蕩運動，而近似地將潛艇的運動看作沿艇艏方向的勻速運動和繞3個坐標軸的搖擺運動，即縱搖、橫搖和艏搖。

潛艇搖擺運動的方程為[1]：

式（7）中：θs、?s和γs分別表示潛艇縱搖角、橫搖角和艏搖角；θsm、?sm和γsm分別表示潛艇縱搖、橫搖和艏搖運動的幅值；θs0、?s0和γs0分別表示潛艇縱搖、橫搖和艏搖運動的初始相位；τθ、τ?和τγ分別表示潛艇縱搖、橫搖和艏搖運動的周期。

3 數值計算結果及其分析

為實現對上述模型的精確計算，文中采用Matlab語言編制了導彈出筒運動模型的計算程序，根據四階五級Runge-Kutta法[10]進行求解計算。

假設導彈質量m=40 t，長度L=12 m，直徑D=2 m，潛艇運動速度vs=3 kn，導彈發射深度H=30 m。

1）對導彈出筒運動模型進行求解，可以得到導彈出筒過程的速度和姿態角等參數隨時間的變化規律，如圖2～5所示。

圖2 速度—時間曲線

圖3 俯仰角—時間曲線

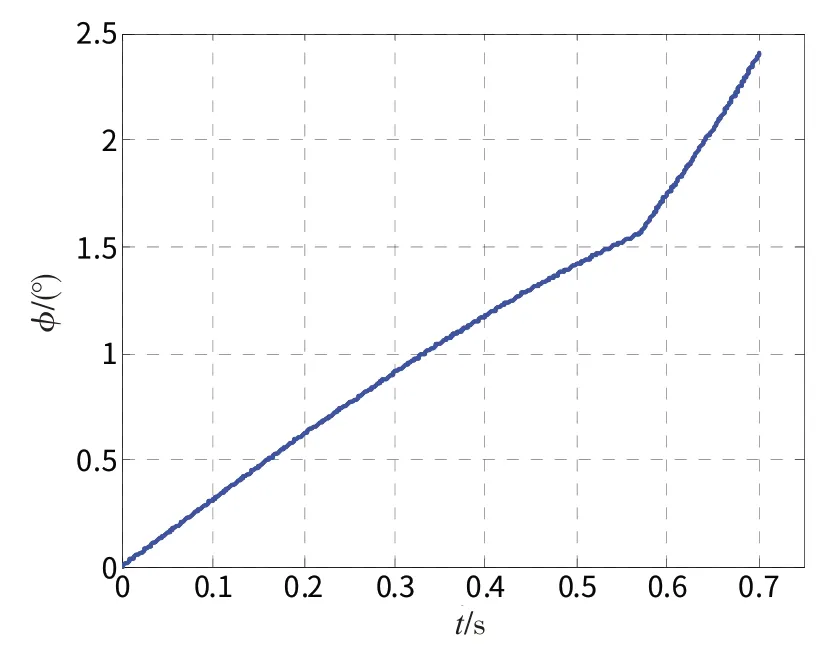
圖4 偏航角—時間曲線

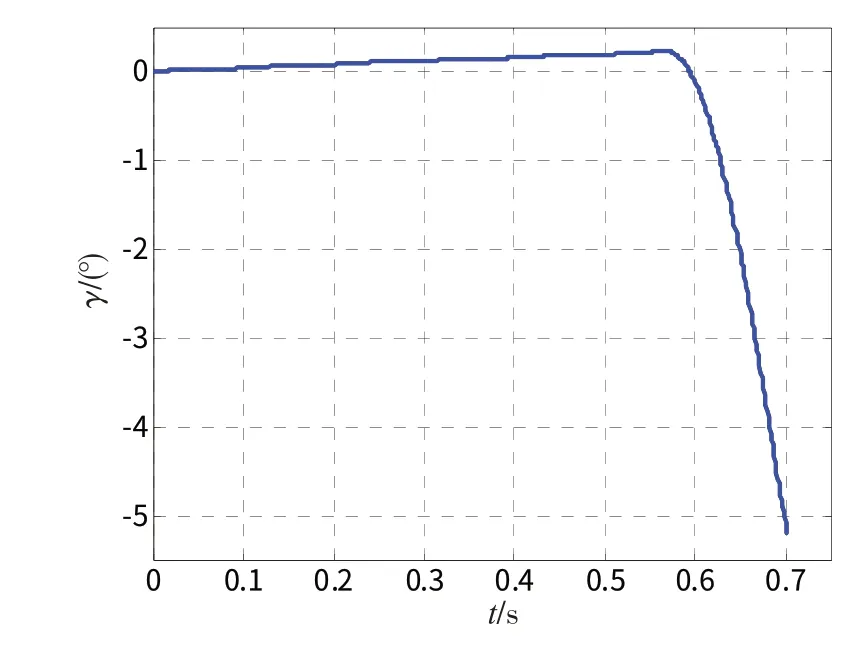
圖5 滾動角—時間曲線

從圖2 中可以看出，導彈在發射筒內的運動時間為0.702 s，導彈出筒速度為34.131 7 m/s。在發射過程中，導彈的速度變化比較平穩。

在第1段中，導彈的運動時間為0.569 s，結束時導彈速度為27.964 m/s。由于導彈與發射筒之間有多圈適配器支撐，導彈受到適配器的力和力矩非常大，因而導彈的姿態角變化比較平穩，導彈的姿態角只與潛艇的搖擺運動有關。

在第2段中，導彈的運動時間為0.133 s，導彈完全離開發射筒時的速度為34.131 7 m/s。由于導彈相對發射筒產生角運動和徑向運動，因而導彈姿態角發生較大的變化。

2）為了分析潛艇的縱搖運動、橫搖運動和艏搖運動隨導彈出筒運動的影響，分別選取考慮搖擺運動、完全不考慮搖擺運動、只考慮縱搖運動、只考慮橫搖運動和只考慮艏搖運動這5 種情況進行仿真計算，計算結果如表1 所示。從表1 的計算結果可見，導彈出筒速度所受到的影響較小，而潛艇搖擺運動對導彈出筒姿態角的變化有比較大的影響，特別是潛艇的縱搖運動對導彈俯仰角、潛艇的艏搖運動對導彈偏航角和導彈滾動角的影響是比較明顯的。其中，導彈俯仰角的變化要小于偏航角和滾動角的變化。

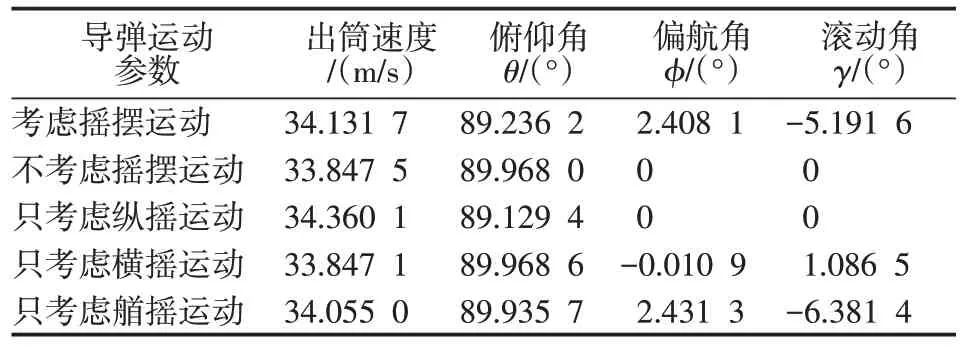
表1 不同搖擺運動的計算結果

3）為了分析潛艇搖擺運動的周期對導彈出筒運動的影響，分別在周期τ、二倍周期2τ和三倍周期3τ這3種情況下進行仿真計算，結果如表2所示。

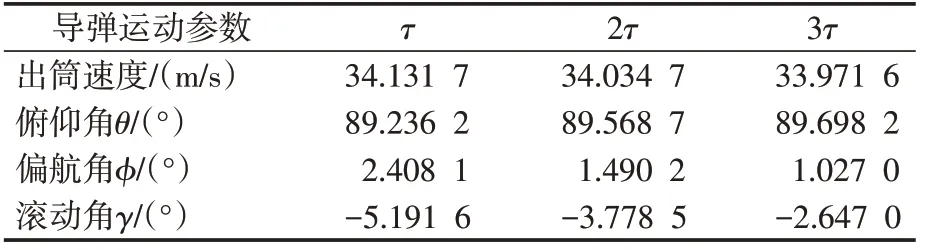
表2 不同周期的計算結果

從表2 的計算結果可見，潛艇搖擺運動的周期對導彈出筒速度影響很小，對導彈出筒姿態影響很大。潛艇搖擺運動的周期越大，導彈出筒姿態越接近垂直。

4 結論

1）通過建模并進行數值仿真計算，可以模擬復雜潛艇運動情況下潛地導彈的出筒運動參數變化，為導彈發射裝置設計和水下彈道計算提供理論參考。

2）計算結果表明，潛艇運動對水下垂直發射導彈的出筒姿態具有一定影響，而潛艇運動是由導彈發射海域決定的。因此，對導彈水下發射環境的監測工作以及對水下發射條件的確定對導彈水下發射可靠性具有十分重要的意義。

[1] 李延軍，郭鳳美，董利強.水下飛行器的彈道仿真[J].導彈與航天運載技術，2009（6）：1-4.

LI YANJUN，GUO FENGMEI，DONG LIQIANG.Trajectory simulation of underwater vehicle[J]. Missile and Space Vehicles，2009（6）：1-4.（in Chinese）

[2] 王聰，王學孝，徐世昌，等.潛射導彈運動特性分析與測試[J].戰術導彈技術，2002（2）：9-12.

WANG CONG，WANG XUEXIAO，XU SHICHANG，et al.Analysis and testing on dynamic characteristics of submarine launched missile[J]. Tactical Missile Technology，2002（2）：9-12.（in Chinese）

[3] 黃壽康.流體動力·彈道·載荷·環境[M].北京：宇航出版社，1991：406-415.

HUANG SHOUKANG. Fluid ballistic load environment[M]. Beijing：Astronautics Press，1991：406-415.（in Chinese）

[4] 方寧，宋召青.潛載垂直發射導彈水下彈道建模與仿真[J].海軍航空工程學院學報，2010，25（3）：311-314.

FANG NING，SONG ZHAOQING.Model and simulation for the underwater trajectory of submarine-based verticallaunched missile[J]. Journal of Naval Aeronautical and Astronautical University，2010，25（3）：311-314.（in Chinese）

[5] 宗瑞良，陳連平，蔣小奎.火箭航行器水中運動數學模型[J].西北工業大學學報，2000，18（2）：254-258.ZONG RUILIANG，CHEN LIANPING，JIANG XIAOKUI. A mathematical model for underwater rocket motion[J]. Journal of Northwestern Polytechnical University，2000，18（2）：254-258.（in Chinese）

[6] 張永，劉曜，胡德斌.基于MATLAB 的潛空導彈運載器的水彈道研究[J].戰術導彈技術，2007（5）：7-10.

ZHANG YONG，LIU YAO，HU DEBIN. Research on capsule’s trajectory of submarine launched missile based on matlab[J]. Tactical Missile Technology，2007（5）：7-10.（in Chinese）

[7] 嚴衛生. 魚雷航行力學[M]. 西安：西北工業大學出版社，2005：106-115.

YAN WEISHENG. The torpedo sailing mechanics[M].Xi’an：Northwestern Polytechnical University Press，2005：106-115.（in Chinese）

[8] 仲維國，張嘉鐘.潛射航行器的水下彈道模擬[J].彈道學報，2005，17（1）：8-12.

ZHONG WEIGUO，ZHANG JIAZHONG. Numerical Simulation of underwater-launched vessel’s submarine trajectory[J].Journal of Ballistics，2005，17（1）：8-12.（in Chinese）

[9] 李咸海，王俊杰.潛地導彈發射動力系統[M].哈爾濱：哈爾濱工程大學出版社，2000：82-83.

LI XIANHAI，WANG JUNJIE. Launch dynamic system of submarine-ground missile[M].Harbin：Harbin Industrial University Press，2000：82-83.（in Chinese）

[10]薛定宇，陳陽泉.高等應用數學問題的Matlab 求解[M].北京：清華大學出版社，2004：209-217.

XUE DINGYU，CHEN YANGQUAN. The Matlab solving of advanced applied mathematics problem[M]. Beijing：Tsinghua University Press，2004：209-217.（in Chinese）