一種泵車臂架模態分析中液壓油缸的等效方法
鐘志宏,吳運新
(1.中南大學機電工程學院,湖南長沙410083; 2.中南大學高性能復雜制造國家重點實驗室,湖南長沙410083)
混凝土泵車是一種用于混凝土澆注的大型工程機械,主要由底盤、混凝土泵和臂架系統組成[1]。其中,臂架系統是最能反映混凝土泵車設備特點的部件,其安全性、可靠性和先進性是決定泵車核心競爭力的關鍵,結構如圖1所示。
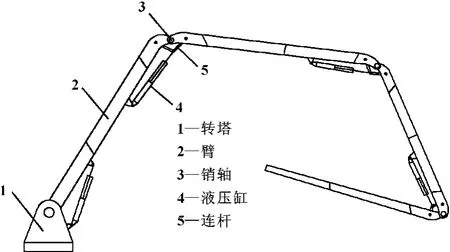
圖1 泵車臂架結構簡圖
實際工作時,臂架姿態可以連續變化,其整體剛度和質量分布也相應變化,進而導致其應力分布及動態特性的變化[2]。因此,了解泵車典型工況下的應力狀態及動態特性如固有頻率和振型,對于泵車的安全使用與維護具有重要的意義。
根據模態理論,在不考慮阻尼影響的情況下,模態主要由系統剛度和質量決定。對于臂架模態分析,通常用二力桿 (Rod)來模擬液壓油缸[1-4],然而其等效剛度如何確定卻鮮有文獻論及。同時,在進行臂架多姿態模態分析時,液壓油缸長度變化但質量基本保持不變,這就要求桿單元的密度也要相應變化以保持質量不變。作者將討論臂架模態分析時液壓油缸等效剛度與等效密度的確定方法,然后依此方法對某臂架模型典型工況進行了模態分析,最后進行了試驗驗證。
1 液壓油缸的等效模型
1.1 等效剛度
1.1.1 液壓油的剛度
在一般液壓系統中,液壓油都被當作剛性不可壓縮的。這是由于液壓油壓縮量較小,其影響在輕載和慢動作系統中微不足道,常常忽略不計。然而在泵車臂架系統中,液壓油微小的壓縮量會在臂架末端產生非常顯著的位移,而液壓油的剛度又遠小于鋼材的剛度,所以液壓油缸的剛度在臂架整體剛度中起著至關重要的作用,從而在限元建模過程中需要準確計算其等效剛度。
在液壓系統中,液壓油實際上以彈簧的方式壓縮,其剛度k可以表示為:

式中:p為壓強;A為壓縮面積;h為壓縮位移。
液壓油的體積彈性模量E定義為在壓強為p時,原始體積V與被壓縮體積量ΔV之比,即:

可推出:

式中:l為油液長度;其他同式(1)。
把式(3)代入式(1),可得液壓油的剛度:

由式 (4)可以看出,液壓油具有和固體材料相同的拉壓剛度公式。
1.1.2 液壓油缸的等效剛度模型
當臂架位于某一姿態時,平衡閥鎖死,因此在計算液壓缸的等效剛度時除了考慮缸內的液壓油之外,還要考慮液壓缸和平衡閥之間的油管內的液壓油的剛度[5],如圖2所示。

圖2 液壓油缸系統原理圖
根據式 (3),當油壓為p時,液壓缸無桿腔端液壓油本身的壓縮位移:

油管內液壓油壓縮位移:

從而可知由于油管內液壓油壓縮而引起的缸內油液位移:

根據式(1)可以計算有桿腔端(帶油管)的液壓油的等效剛度:

把式(5)—(7)代入(8),得

類似的,可知無桿腔端 (帶油管)液壓油的等效剛度:

圖2所示整個液壓缸系統可以等效為如圖3所示的彈簧質量系統。
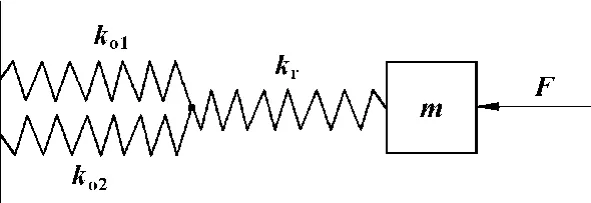
圖3 液壓油缸等效剛度模型
圖3中ko1、ko2分別為液壓油缸有桿腔端和無桿腔端液壓油的等效剛度;kr為活塞桿的剛度,亦符合式(4)。
根據彈簧聯接理論,圖3所示系統的等效剛度為:

綜上,臂架在任意姿態時可按上述方法計算液壓油缸的等效剛度。
1.2 等效密度
臂架姿態變化時,液壓缸長度變化但質量不變,在用桿單元等效時可以通過調節桿單元的材料密度ρeq來實現:

式中:m為液壓油缸總質量;A為桿單元截面積;l為某姿態下液壓缸(桿單元)長度。
2 典型工況模態算例
臂架工作時姿態多變。姿態不同,臂架整體的質量和剛度分布也會發生變化,因此其固有頻率及振型也不相同。作者僅選取某臂架地基和面墻兩種典型姿態運用MSC.Patran/Nastran進行模態分析,兩種姿態下每節臂與水平方向的夾角分別為 [75°,15°,-15°,-75°]、[75°,45°,0°,-45°]。
對比分析結果,發現兩種姿態下臂架振型類似,但固有頻率有明顯差異。因篇幅關系,文中只列出地基工況下臂架前六階模態振型,如圖4所示。其中,第一、四、五階振型為臂架側向擺振;第二、三、六階為臂架自身平面 (x-y平面)內的振動。兩種姿態下臂架前六階固有頻率見表1。

圖4 地基工況下臂架前六階振型

表1 臂架前六階固有頻率 Hz
3 試驗驗證
3.1 試驗方案
通過實驗模態分析獲取臂架系統振型和固有頻率的方法復雜,故常用負階躍激振后測量臂架自由振動時域曲線,然后進行頻譜分析獲取系統一階固有頻率的方法[6-7]。因為臂架固有頻率較低 (低于1 Hz),如果采用加速度傳感器則需要傳感器具有良好的低頻精度,否則將影響試驗精度,而這種傳感器價格較高。因此,從精度和經濟方面考慮,試驗采用應變測量。
操作臂架分別運動至上述兩種典型姿態,然后在豎直方向拖拽第四節臂末端使臂架發生自身平面內的振動,松開后開始記錄臂架自由振動的時域曲線。對時域曲線進行FFT變換獲取臂架幅頻譜,從而可知對應姿態下臂架自身平面內振動的一階固有頻率(對應模態分析中二階固有頻率)。
3.2 數據處理與分析
3.2.1 地基姿態
地基姿態臂架振動時域曲線及對應頻域曲線分別如圖5、圖6所示。由圖6可以看出,臂架地基姿態自身平面內振動的一階固有頻率為0.829 Hz,而對應有限元模態分析所得固有頻率為0.877 27 Hz,從而可以計算出仿真分析對于試驗數據的相對誤差為5.82%。

圖5 地基姿態時域曲線

圖6 地基姿態幅頻譜
3.2.2 面墻姿態
面墻姿態臂架振動時域曲線及對應頻域曲線分別如圖7、圖8所示。由圖8可以看出,臂架面墻姿態自身平面內振動的一階固有頻率為0.780 7 Hz,而對應有限元模態分析所得固有頻率為0.814 52 Hz,從而可以計算出仿真分析對于試驗數據的相對誤差為4.33%。

圖7 面墻姿態時域曲線

圖8 面墻姿態幅頻譜
4 結論
首先建立了泵車臂架多姿態模態分析時液壓油缸的等效模型,推導了其剛度與密度計算公式,然后對臂架的兩種典型姿態即地基與面墻進行了模態分析,最后對兩種姿態下的臂架進行了固有頻率試驗。通過有限元分析結果與試驗結果對比發現,仿真分析結果與試驗數據誤差小于6%,從而驗證了文中提出的液壓油缸等效模型的準確性。
【1】史先信,鄭永生,徐懷玉,等.基于ANSYS的大型泵車臂架有限元分析[J].建筑機械,2009(4):79-82.
【2】吳運新,鐘志宏,滑廣軍.基于MSC.Patran/Nastran的泵車臂架分析系統的研究[J].鄭州大學學報:工學版,2010,31(6):83-86.
【3】張艷偉,佟力,孫國正.基于ANSYS的混凝土泵車臂架結構分析研究[J].武漢理工大學學報:交通科學與工程版,2004,28(4):536-539.
【4】宋建安,董忠紅,呂彭民.水泥混凝土輸送泵車整機模態[J].長安大學學報:自然科學版,2004,24(5):104-106.
【5】戴云飛.液壓缸液壓剛度的計算[J].有色金屬設計,1999,26(1):61-63.
【6】呂彭民,汪紅兵,張大慶.混凝土泵車結構模態分析與試驗[J].長安大學學報:自然科學版,2004,24(6):74-76.
【7】王海英.水泥混凝土泵車振動性能與結構優化設計研究[D].西安:長安大學工程機械學院,2003.

