少節點基因調控網絡的控制*
葉緯明 呂彬彬 趙琛 狄增如
1)(北京師范大學管理學院系統科學系,北京 100875)
2)(北京有色金屬研究總院稀土材料國家工程研究中心,有研稀土新材料股份有限公司,北京 100088)
(2012年7月18日收到;2012年7月31日收到修改稿)
1 引言
隨著生物技術的不斷發展,基因工程被不斷向前推進,海量的數據為科學家探索基因的奧秘提供了有力的支持,大量生物組織的基因被成功測序.對基因調控網絡(genetic regulatory network,GRN)的研究也越來越受到各個領域的關注.其中,基因調控網絡的振蕩問題一直是大家關注的熱點之一[1-13].早在30年前,Thomas就曾提出:基因調控網絡要想形成振蕩,就必需至少要有一個負反饋環(環上負反饋的個數為奇數).該論斷于1995年被嚴格證明是正確的[14,15].近年來,該領域涌現出大量的科研成果.Goh等[16]認為基因調控網絡是否能夠形成振蕩主要取決于網絡中正負反饋環之間的競爭,如果負反饋環占優,網絡呈現振蕩態;如果正反饋環占優,網絡則會呈現穩定態.2000年,Elowitz和Leibler等[17]成功地在實驗室中制造出了首個振蕩的3節點生物網絡.它包括3個轉錄抑制蛋白,每個抑制蛋白都抑制下一個基因的轉錄,當某種特殊蛋白質含量發生變化時,細胞能在發光狀態和非發光狀態之間轉換,形成一個環狀回路,起到有機振蕩器的作用.2002年,U.Alon發現在真實的生物網絡中存在一系列非常小的結構單元(被命名為“模體”),它們在網絡中出現的頻率很大,并且對網絡的功能起著非常大的作用.至此,大家開始把目光轉移到這些小的結構單元上來,希望通過對這些模體的研究來逐漸認識整個基因網絡.2006年,Nochomovitz和Li[18]運用布爾代數的方法研究了所有3節點和4節點的網絡,發現這種少節點的網絡中有許多是可以形成振蕩的.
目前我們發現的大多數基因調控網絡在大部分時間里都是處于靜息態的,只有當網絡受到外界刺激時,它們才會被激發到振蕩態,完成各種生物功能,然后再回到靜息態等待下一次刺激.對于一個原本應該處于靜息態的基因調控網絡,如果因為某種原因跳到了振蕩態上,那么它就會不斷地重復某種生物過程,導致機體功能紊亂,同時它對外界的刺激也可能不再敏感,使生物體處于嚴重失控狀態.因此對基因調控網絡的控制就顯得非常重要了.
目前對生物網絡的控制研究主要集中在神經網絡[19,20]、蛋白質相互作用網絡,對基因調控網絡方面的控制還不是很多,特別是如何將一個振蕩的基因調控網絡控制到靜息態的研究還非常少[21].本文運用多相位超前驅動方法對基因調控網絡的控制進行了研究.通過大量的數值模擬,發現對于參數已經確定的基因調控網絡,此方法的控制效率可以達到95%以上(10節點網絡),對于參數不確定的網絡,此方法的控制效率也非常高.
2 基因調控網絡動力學模型
這里我們運用目前廣泛采用的描述基因聯合調控的動力學模型[21-25].它在抑制調控和促進調控中采用“AND”門的形式.具體的動力學模型如下:

這里xi表示第i個節點的濃度,acti(repi)代表促進(抑制)轉錄因子的總和.動力學(1)中一共有5個系統參量.μ表示在沒有促進作用和抑制作用時的漏轉錄率;K是網絡中促進子(抑制子)調控時的半高濃度;h是希爾系數;γ代表衰減率;表示第j個節點對第i個節點促進(抑制)作用的權重.
動力學(1)是一種強抑制模型[26],對所有的抑制調控采用“AND”門的形式[25],而對所有的促進調控采用“OR”門的形式.為了使系統具有一般性,我們讓網絡中所有節點的參數相同.(μi=μ=0,γi=0.1,hi=2,Ki=0.3,αi=βi=1,i=1,2,···,N[27]).
3 數值模擬
3.1 主相位超前驅動方法
主相位超前驅動(dominant phase advanced driving,DPAD)思想最先是由Hu等[19,20]提出,并用于對神經網絡的控制中.其主體思想是:對于一個隨機的網絡,網絡當中每一個節點都是不能自發產生 振蕩的,它們如果想形成振蕩就必須受到別的節點的驅動,當然這里的驅動可以來自一個節點也可以來自多個節點,但必需至少要有一個來自外界的驅動.可以通過一系列的定義找到網絡中每個節點的驅動點(作為這個節點的上游節點).再通過一定的定義即可以從每個節點的所有上游節點中找出對其影響最大的節點,該節點的驅動即為主超前相位驅動(其他上游節點的驅動此時可以去掉).這樣網絡中的每個節點都將有且只有一個主超前相位驅動,即每個節點都只剩下一個上游節點,這樣整個網絡必定會變成一個一維環狀結構.運用這種方法找到的環狀結構對于神經網絡的調控具有非常重要的意義.而將這種方法應用到基因調控網絡中,找到的環狀結構也意義非凡[21].如圖1所示,圖1(a)為一個10節點的隨機振蕩基因調控網絡,圖1(b)為運用主相位超前驅動方法找到的環狀結構.從這種環狀結構中不僅可以清楚地找到振蕩基因調控網絡的振蕩源,還可以看到網絡信號在網絡中的傳播路徑,同時還能粗略地看出網絡中重要的和不重要的節點(分別用紅色和白色表示),有利于對網絡進行調控.
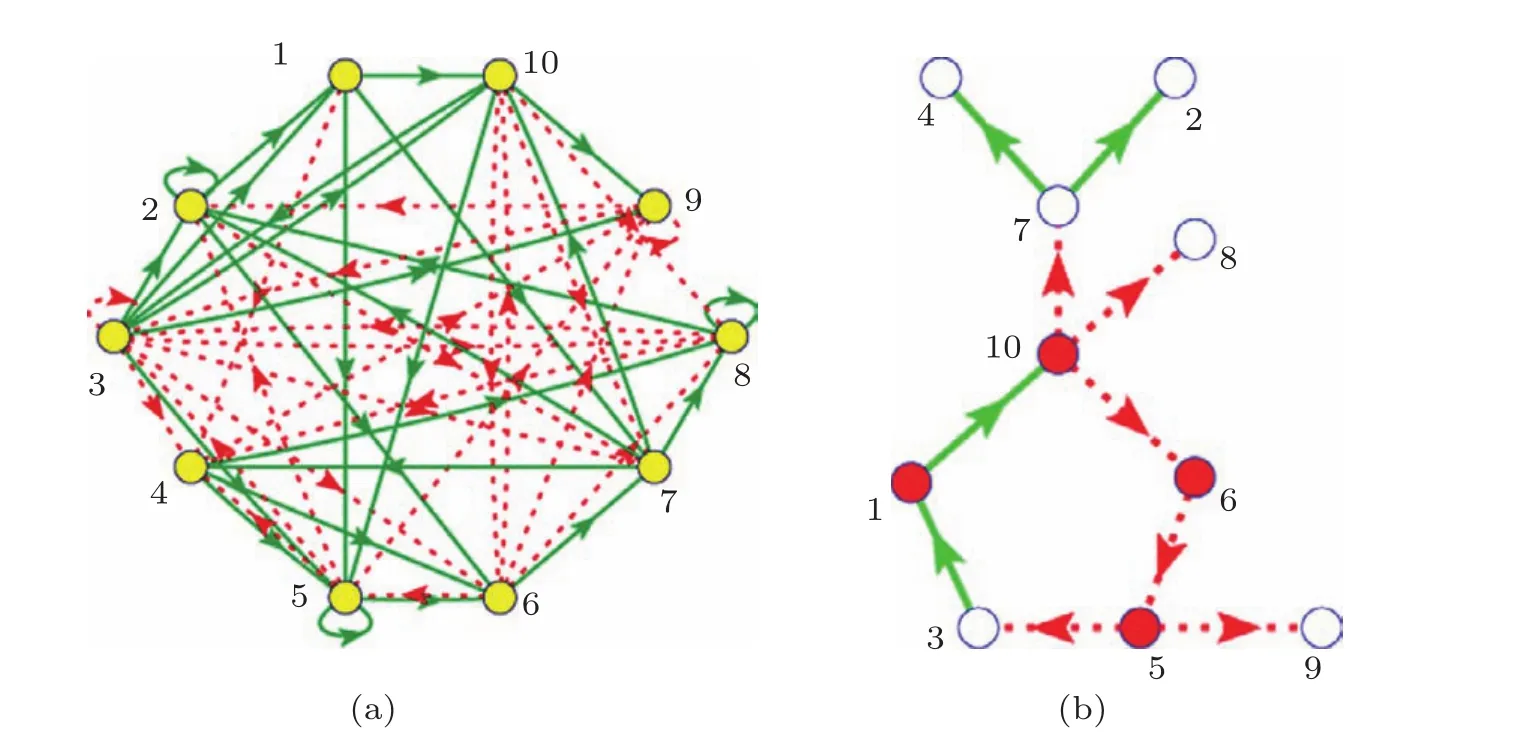
圖1 少節點基因調控網絡 (a)10節點隨機振蕩基因調控網絡,其中綠色實線表示促進作用,紅色虛線表示抑制作用;(b)運用主相位超前驅動方法找到的一維環狀結構,其中重要節點用紅色表示,不重要的節點用白色表示
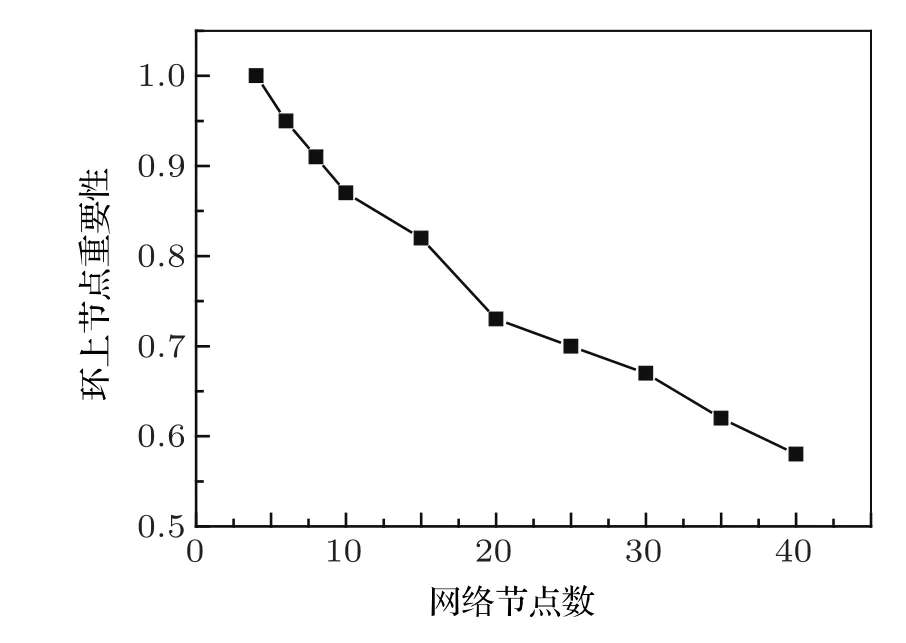
圖2 不同節點數的基因調控網絡,主相位超前驅動環上的節點重要性
這里,網絡中重要的節點指的是去掉這個節點網絡就會從振蕩態到達穩定態;不重要的節點指的是去掉這個節點,網絡的振蕩態不會發生改變.運用主相位超前驅動方法對原始網絡進行簡化,可以得到:對于少節點的網絡,重要的節點幾乎都在環上,不重要的節點幾乎都在環外.但是隨著網絡節點數的增多,主相位超前驅動方法在區分節點的重要性上就會弱化.環上的節點不再重要的概率會逐漸增高.如圖2所示,經過大量的數值模擬可以看出,當網絡節點數少于10個時,環上的節點是重要節點的概率超過了90%;而當網絡上的節點多于10個時,環上節點是重要節點的概率近似以線性比例下降;當網絡節點數達到40個時,環上節點為重要節點的概率下降到只有57.9%.
3.2 多相位超前驅動方法
我們對主相位超前驅動方法做了適當的修改,將之變為多相位超前驅動方法.運用這種方法可以將找到重要節點的概率大大提高.具體的做法如下:1)給網絡中每個節點定義一個相位[21];2)找出每個節點的上游節點(將上游節點指向下游節點的連邊定義為重要連邊);3)簡化原始網絡,將網絡中的重要連邊留下,組成相位超前驅動網絡;4)找出相位超前驅動網絡中所有的負反饋環;5)統計相位超前驅動網絡中每個節點參與的負反饋環數并排序.如圖3所示,圖3(a)為圖1(a)的相位超前驅動網絡,圖3(b)為其相位超前驅動網絡中所有的負反饋環(共11個).各個節點的數據統計見表1.從表1可以看出:在相位超前驅動網絡中,10號節點參與的負反饋環數最多,它是一個重要節點,控制住它,就可以控制整個網絡.同時還可以看出節點參與負反饋環數排名中的前6位都是重要節點.而后4位都是不重要的節點.可見這一方法對于判斷節點的重要性具有很好的效果.
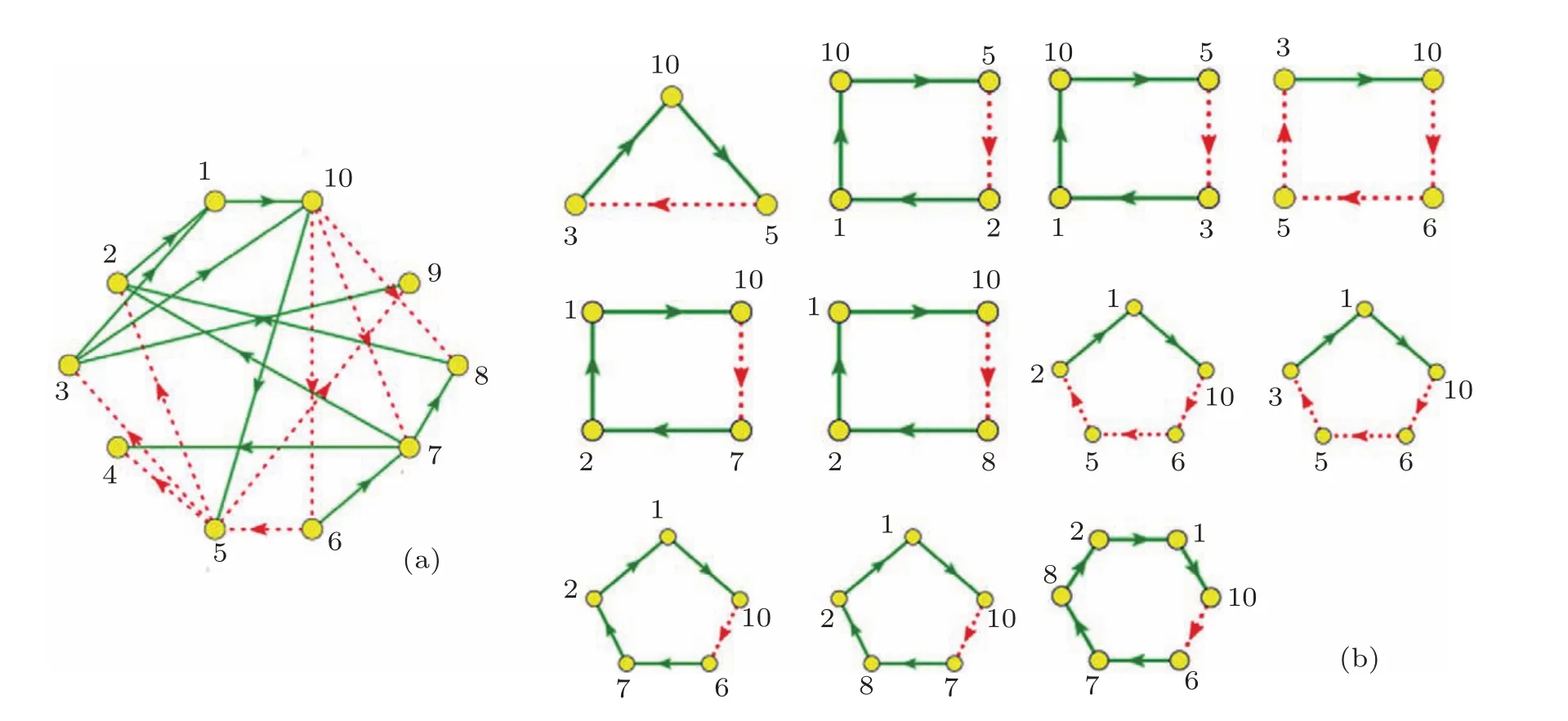
圖3 相位超前驅動網絡 (a)圖1(a)的相位超前驅動網絡;(b)(a)圖中所有的負反饋環
數值模擬結果表明:隨機選取10000個振蕩網絡,運用多相位超前驅動方法對節點參與負反饋環的排序,排在第一位的節點(以下稱為“首要節點”)是重要節點的概率比用主相位超前驅動方法尋找重要節點的概率要高很多.如圖4所示,可以看出運用多相位超前驅動方法找到的首要節點是重要點的概率并沒有隨著網絡節點數的增加而大幅度下降.當網絡節點數達到40個節點時,首要節點為重要節點的概率依然可以達到90%.
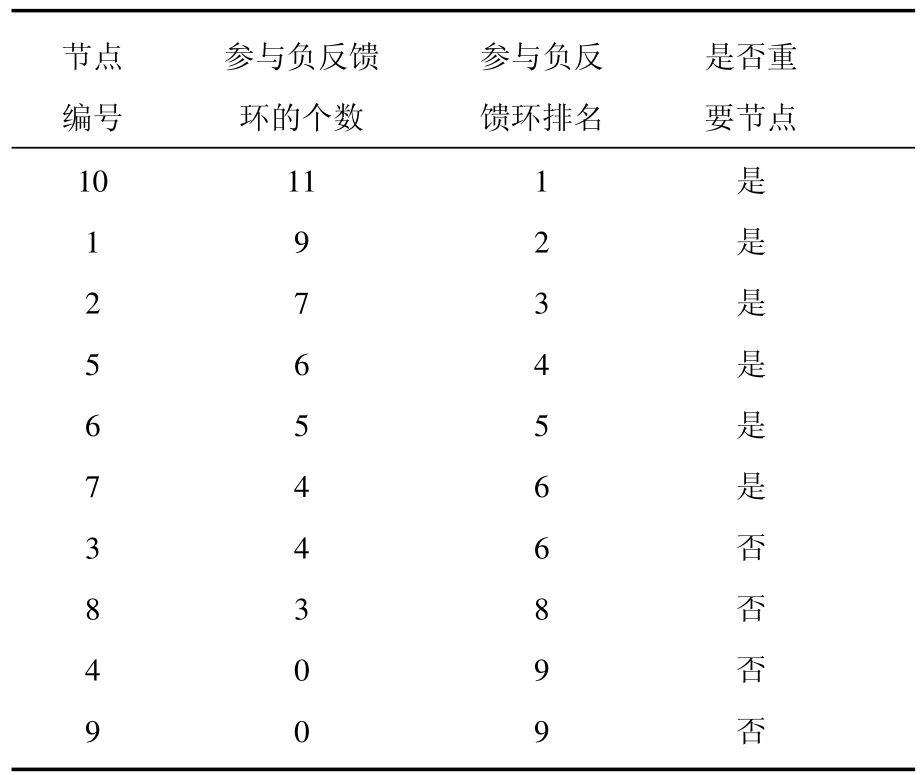
表1 多相位超前驅動法判斷節點的重要性(參數確定)
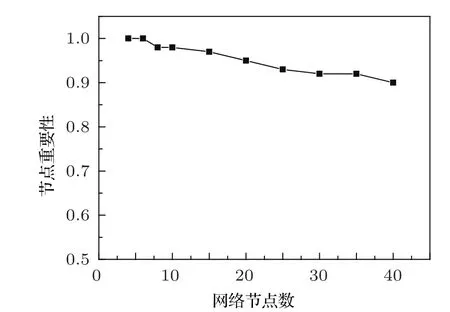
圖4 不同節點數的基因調控網絡,運用多相位超前驅動方法找到的首要節點為重要節點的概率
以上是在系統參數確定的情況下,運用多相位超前驅動方法尋找網絡重要節點的結果.那么當系統的參數不確定時,如何來尋找網絡的重要節點呢?數值模擬表明運用多相位超前驅動方法依然可以有效地找到網絡中的重要節點.具體方法是:將系統參數在其各自有效的范圍內[27]劃分為若干個點,然后在每個參數點上統計出各個節點在相位超前驅動網絡上參與的負反饋環的個數,最后統計在所有參數點上各個節點在相位超前驅動網絡上參與的負反饋環的總個數,并依此排序.
還是以圖1(a)所示的網絡為例.通過數值模擬,我們發現:運用多相位超前驅動方法找到的在所有參數點上的相位超前驅動網絡中參與負反饋環最多的節點(10號節點,以下稱為“頭號節點”),其平均重要性達到了100%(這里的平均重要性指的是:對所有的參數點[27],控制目標節點后,網絡能夠被有效控制到穩定態的平均概率),其他節點的平均重要性見表2.從表2可以看出:網絡節點的平均重要性與其參與的負反饋環的總排名關系很大.
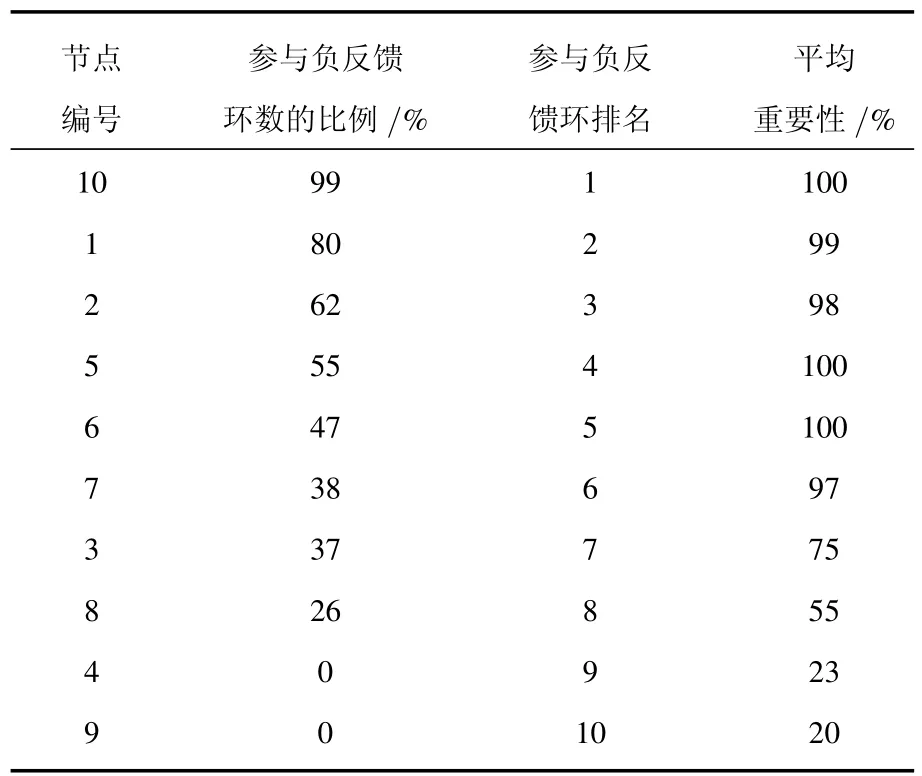
表2 多相位超前驅動法判斷節點的重要性(參數不確定)
我們用數值模擬的方法對10000個10節點的網絡進行了統計,結果表明:在系統參數不確定的情況下,運用多相位超前驅動方法找到的頭號節點,其平均重要性為100%的概率為92%.對于其他節點數的網絡,我們也做了類似的統計,結果如圖5所示.
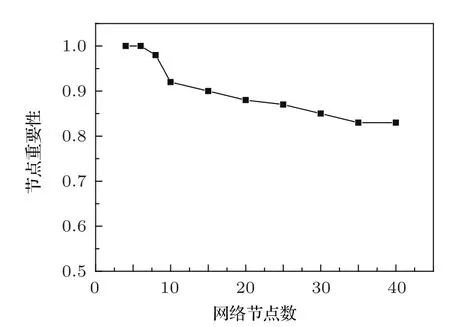
圖5 不同節點數的基因調控網絡,頭號節點平均重要性為100%的概率
我們認為多相位超前驅動方法之所以比主相位超前驅動方法能更好地尋找到網絡當中的重要點,是因為在主相位超前驅動中只保留了對被驅動節點貢獻最大的上游節點,而忽視了其他上游節點的作用.這樣就導致了網絡簡化過程中只保留下來惟一一個負反饋環,并被認為是網絡振蕩的源.從數值統計上看,這惟一一個負反饋環上的節點是重要節點的概率比環外的節點要高很多.但這其中還是有節點是不重要的,它們出現在環上也許只是因為其所控制的下游節點只有它這一個上游節點,或者有多個上游節點但是每個上游節點的貢獻都很小.而運用多相位超前驅動方法就可以很好地避免上面的問題.在多相位超前驅動中,我們將原始網絡中所有的重要連邊都保留下來,形成相位超前驅動網絡,該網絡是對原始網絡的簡化,同時又保留著原始網絡中的重要信息.根據Goh等[16]的理論,以及我們之前的一些研究結果表明:負反饋環對于網絡的振蕩起著促進作用(當然這其中各種負反饋環所起的作用大小不同,但是定性上來說還是促進的[28]),那么簡化后的網絡中,每個負反饋環上的節點應該都對網絡的振蕩起著一定的作用.如果把這些作用累加起來,就可以看作是該節點對網絡振蕩所起的總貢獻,這樣總貢獻的排序即可以在一定程度上反映網絡中節點的重要性.
4 結論
基因調控網絡是目前大家研究的一個熱點,而它的自組織振蕩又是其中的核心問題.如何來控制自組織振蕩是問題的關鍵.主相位超前驅動方法對于少節點的網絡可以較好地找到網絡中的重要節點,但是對于節點數較多的網絡,這種方法找到重要節點的概率會呈線性下降.運用多相位超前驅動方法則可以很好地解決上述問題.對于系統參數已經給定的網絡,運用該方法找到重要節點的成功率明顯提高.對于系統參數不確定的網絡,運用該方法也可以高效率地找到網絡中的重要節點.
[1]Tavazoie S,Hughes J D,Campbell M J,Cho G M 1999Nat.Genet.22 281
[2]Xu P X,Zhang X,Heaney S,Yoon A,Michelson A M,Maas R L 1999Development126 383
[3]Peterson K J,Davidson E H 2000P.Natl.Acad.Sci.USA97 4430
[4] Lee T I,Rinaldi N J,Robert F,Odom D T 2002Science298 799
[5]Ihmels J,Friedlander G,Bergmann S,Sarig O 2002Nat.Genet.31 370
[6]Ma H W,Kumar B,Ditges U,Gunzer F 2004Nucleic Acids Res.32 6643
[7]Posfai G,Plunkett G 2006Science312 1044
[8]Gilchrist M,Thorsson V,Li B,Rust A G 2006Nature441 173
[9]Kurland C G,Collins L J,Penny D 2006Science312 1011
[10]Mcadams H H,Srinivasan B,Arkin A P 2004Nature Rev.Genet.5 1
[11]Shen-Orr S S,Milo R,Mangan S,Alon U 2002Nat.Genet.31 64
[12]Lipshtat A,Purushothaman S P,Lyengar R,Maayan A 2008Biophysical Journal94 2566
[13]Kim J R,Yoon Y,Cho K H 2008Biophysical Journal94 359
[14]Snoussi E H 1998J.Biol.Sys.6 3
[15]Plahte E H,Mestl T,Omholt W S 1995J.Biol.Sys.3 409
[16]Goh K G,Kahng B,Cho K H 2008Biophysical Journal94 4270
卓別林有一句很幽默的名言:“人們為我歡呼,是因為他們對我了如指掌;人們為愛因斯坦歡呼,是因為沒人弄得懂他。”的確,電影不同于高深的物理理論,卓別林用最直接的方式向不同層次的觀眾們傳達著自己想要表達的觀點,這是人們喜歡他的原因。
[17]Elowitz M B,Leibler S 2000Nature403 335
[18]Nochomovitz Y D,Li H 2006P.Natl.Acad.Sci.USA103 4180
[19]Qian Y,Liao X,Huang X,Hu G 2010Phys.Rev.E 81 036101
[20]Liao X,Hu G 2011Front.Phys.6 124
[21]Ye W,Huang X,Li P,Hu G 2010Phys.Lett.A 374 2521
[22]Li C,Chen L,Aihara L S,Kazuyuki L 2006IEEE53 2451
[23]Mangan S,Alon U 2001P.Natl.Acad.Sci.USA100 11980
[24]Setty Y,Mayo A E,Surette M G,Alon U 2003P.Natl.Acad.Sci.USA100 7702
[25]Ishilara S,Fujimoto K,Shibata T 2005Genes to Cells10 1025
[26]Wu Y,Zhang X,Yu J,Ouyang Q 2009PLoS Computational Biology5 e1000442
[27]Ye W,Li P,Huang X,Hu G 2010Phys.Lett.A 374 4749
[28]Ye W,Zhang Z,L¨u B,Di Z,Hu G 2012Chin.Phys.B 21 060203

