距離與多普勒二維長時間相參積累方法

劉俊豪， 陳 潛， 陸滿君

（上海無線電設備研究所，上海200090）

0 引言

隨著隱身技術和高性能武器裝備的發展，飛機、導彈等目標的雷達散射截面積（RCS）降低了一到兩個數量級，使現有雷達系統的探測距離范圍減小，檢測性能大為降低，在現代雷達中常采用增加積累時間的方法提高隱身等微弱目標的檢測性能［1-3］。而在長時間相參積累過程中，由于雷達與目標之間相對距離、相對速度變化引起的距離走動、多普勒擴散現象，嚴重影響目標能量的積累和檢測。

因此，研究有效的校正距離走動和多普勒擴散補償方法是改善現代雷達檢測性能的重要途徑之一［1］。

長時間相參技術中，對距離校正和多普勒補償的方法很多。其中，Keystone變換的方法能在未知速度的情況下進行距離走動盲補償，文獻［3～5］對Keystone變換的原理和快速算法進行闡述，其可以對一定速度范圍內的跨距離單元進行統一補償，但是未考慮多普勒擴散問題。對多普勒擴散的補償，文獻［6～8］分別采用Hough-Wigner變換、分數階傅里葉變換、短時傅里葉變換等時頻分析的方法，由于時頻分析過程中雙線性變換運算量大，本文采用文獻［1］提出的Dechirp方法。

本文將Keystone變換和Dechirp方法結合，解決距離和多普勒二維走動問題，并采用Chirp-Z變換快速實現Keystone變換減小運算量，最后通過仿真分析驗證算法的有效性和檢測性能。

1 信號模型

假設雷達發射LFM 信號，對于勻加速運動單點目標回波信號一個相參積累間隔（CPI）內雷達接收到的第m 個回波基帶信號為

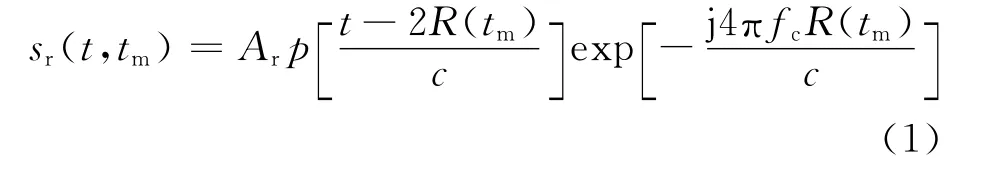
式中：t和tm分別為快時間和慢時間（tm＝mT，其中T 為脈沖重復間隔（PRI））；fc為載波頻率；c為光速；Ar為點目標的回波幅度；R（tm）＝R0+vtm+0.5atm2，其 中a 為 目 標 徑 向 加 速 度；R0和R（tm）分別為t0和tm時刻目標相對于雷達的徑向距離；p（t）＝rect（t／Tp）exp（jπγt2）為發射的LFM信號。

式（1）的頻域形式：

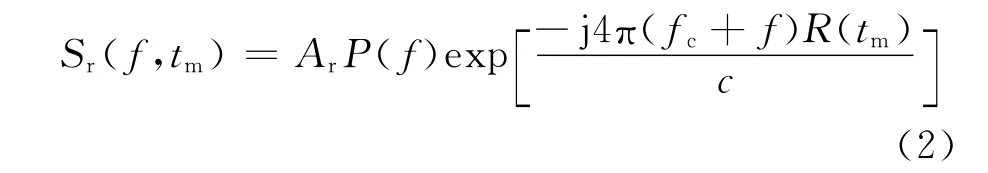
式中：P（f）為p（t）的頻域。上式在距離頻域乘以P＊（f）進行匹配壓縮，得

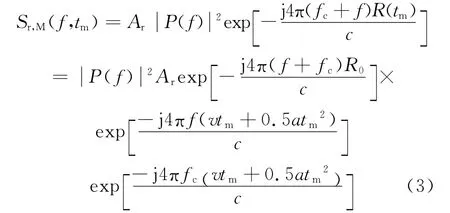
式中：第二個指數項中v和a 引起距離走動；第三個指數項中a引起多普勒擴散。

式（3）的時域形式為

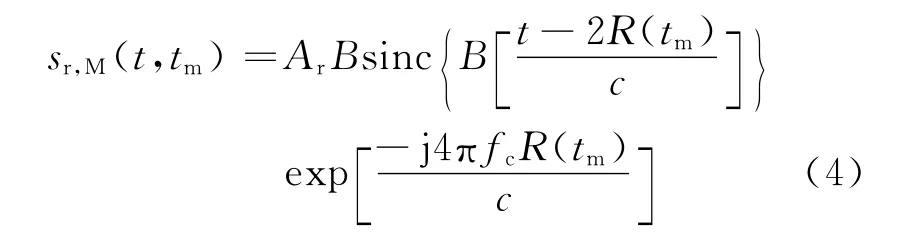
基帶回波通過脈沖壓縮后其包絡為離散sinc函數，其中心頻率在2R（tm）／c處。

因此，目標的速度和加速度會造成每個回波脈沖壓縮之后包絡中心都不同，從而引起跨距離走動。而加速度對多普勒相位的影響，相當于產生一個線性調頻信號，從而產生多普勒擴散現象。

2 距離和多普勒二維補償算法原理

2.1 Keystone變換對距離走動補償

式（3）中多普勒頻率隨慢時間變化，為了消除這種變化，定義虛擬時間τm，其與慢時間的關系為

式中：β為Keystone變換系數。

變換之后在f-τm平面，原來的信號采樣點隨慢時間呈梯形格式（或Keystone形格式），因此稱為Keystone變換。

對式（3），在快時間頻域信號作變量代換，即完成Keystone變換。變換后為

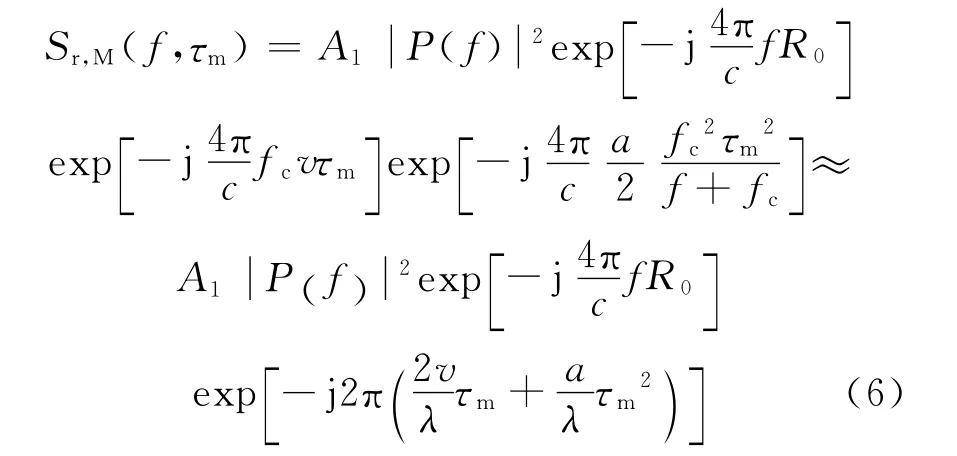
式中：A1＝Arexp（-j4πfcR0／c）。在式（6）相位項中，因為fc?B，故fc／（f+fc）≈1。

Keystone變換后的時域形式：

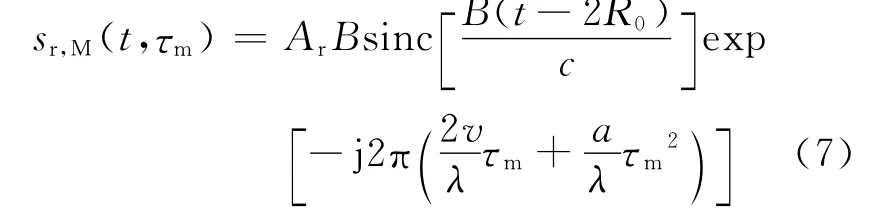
式（7）可以知道，sinc函數代表的距離包絡已經得到校正。為了便于數據處理，Keystone變換可以在f-τm平面通過插值將數據格式變成矩形。但是插值運算量大，下面通過離散化推導出在頻域處理的快速算法過程。

設快時間t和慢時間tm的離散采樣順序分別為n和m，并設采樣點總數分別為N 和M。

兩個時間變換的頻域分別為距離頻率域（f）和多普勒域（fd），分別用l和k 表示，而兩者的采樣總數分別為L 和K，且有N＝L，M＝K。信號帶寬為B，則f＝lB／L，tm＝mT。并令η＝B／（fcL），于是有

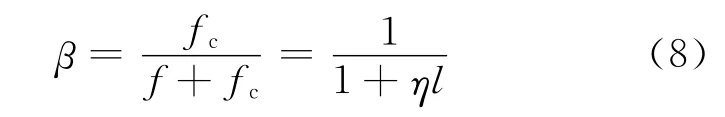
由于加速度對包絡走動的影響較小，而Keystone變換主要完成包絡的校正，對式（3）不考慮加速度，其離散形式為

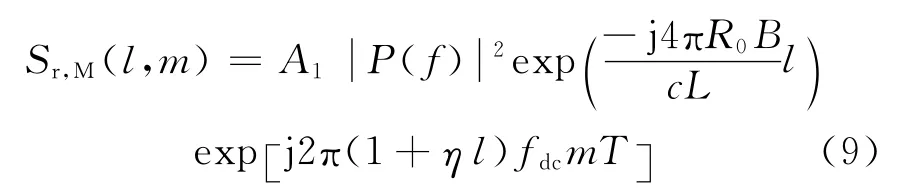
式中：fdc＝-2vfc／c。將虛擬時間τm離散采樣的順序以m′表示，其采樣總數為M；與虛擬時間τm相對應的虛擬離散多普勒采樣點的順序以k′表示，其總數為K′（＝K＝M）。

因此，將Sr，M（l，m）轉換為Sr，M（l，m′），即完成Keystone變換。

可以通過傅里葉變換將Sr，M（l，m）變換到Sr，M（l，k′），然后通過逆傅里葉變換得到Sr，M（l，m′）。變換如下：

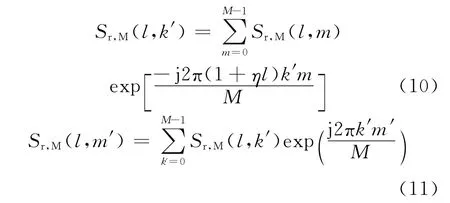
對于式（11）可以通過IFFT 實現，而對于式（10）指數項非均勻DFT 形式，傅里葉變換不能用FFT 實現。

對于該問題，采用線性調頻Z 變換（CZT）的方法將DFT 轉化成FFT 實現，可以大大降低運算量。

令a＝1+ηl，式（10）變換為

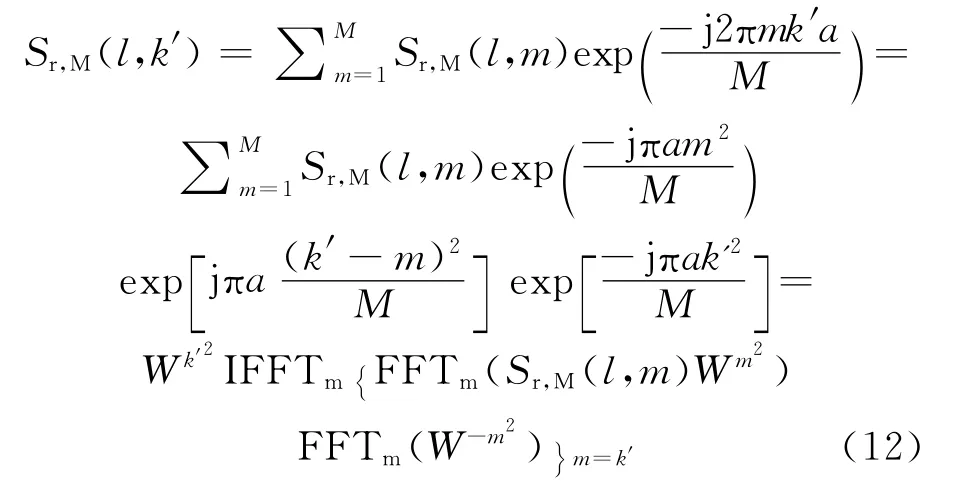
式中：W ＝exp（-jπa／M）；傅里葉變換對變量m進行運算。上式得到快時間頻域和慢時間頻域，將其快時間維做IFT 得到距離和多普勒維的相參積累結果Sr，M（n，k）。

在欠采樣時，對多普勒模糊數的補償只需在Keystone變換后，乘以補償因子：

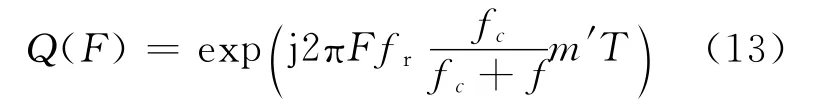
式中：F 為多普勒模糊數，fr為脈沖重復頻率（PRF）。

在實際實現過程中需要對多普勒模糊數進行搜索，如果在末制導尋的雷達中，可以利用預裝信息減少對模糊數的搜索，整個補償過程如圖1所示。

2.2 Dechirp對多普勒擴散的補償

包絡校正后如式（7），此時還受到加速度引起的多普勒相位調制的影響，需要對多普勒進行補償，然后才能相參積累。

對多普勒走動補償采用解線性調頻（Dechrip）的方法。將式（7）乘以exp［j2π（a′／λ）］，當a’＝a時，二次相位得到補償，從而使相位隨時間均勻變化，然后通過FT 實現相參積累。a′可以按照下式進行估計

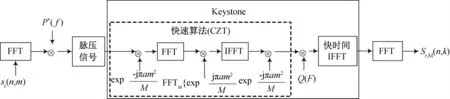
圖1 Keystone變換快速實現流程圖

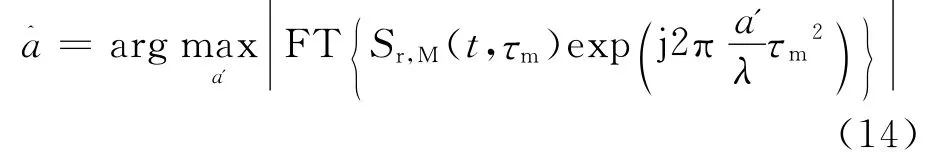
在加速度范圍內，以步進的方法對加速度進行搜索，對得到加速度對應的積累峰值，然后選大處理、恒虛警檢測，確定目標是否存在，并給出目標的距離、速度、加速度信息。

3 仿真實驗與分析

為了驗證算法的有效性和檢測性能，現對所采用的算法進行計算機仿真。

目標和雷達參數：設單點目標相對速度v＝2500m／s，加速度為500 m／s2相向雷達運動，加速度的最大搜索值為600m／s2；載頻為10GHz，信號帶寬B＝20 MHz，時寬Tp＝4μs，采樣頻率fs＝20 MHz，重頻PRF＝25kHz，相參積累脈沖數N＝4096。

相參積累時間為163.8 ms，距離分辨率ΔR＝7.5m，跨距離單元數為54，跨多普勒單元為894。仿真過程中加入SNR＝-10dB的高斯白噪聲，仿真過程的結果如下。

圖2是對接收信號進行匹配壓縮，在噪聲中能夠看出包絡走動現象。直接對包絡進行FFT操作，即動目標檢測（MTD）的結果如圖3、圖4所示，其中圖4是圖3的俯視圖。在相參積累時間內，直接MTD 使回波能量分散在多個距離和多普勒單元（圖4），也正是這個原因使得積累幅度不高，檢測性能較差。

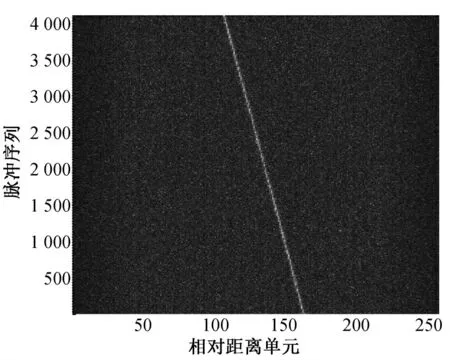
圖2 匹配壓縮包絡軌跡

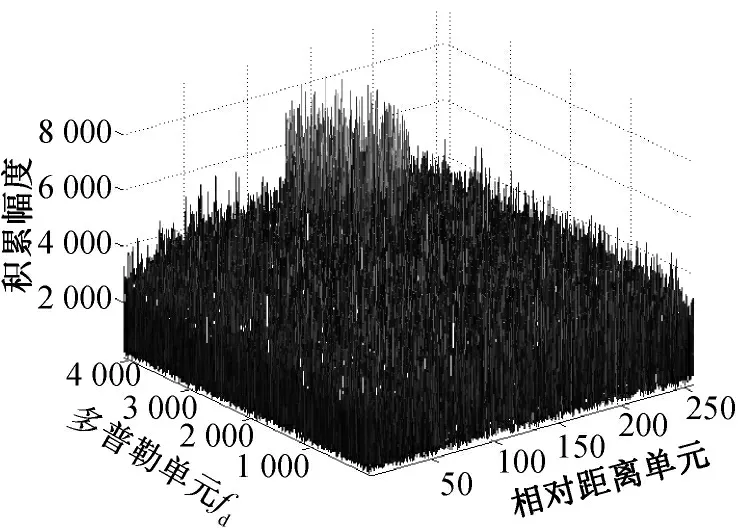
圖3 MTD 結果

圖4 MTD 結果俯視圖

對包絡做Keystone變換使包絡對齊，結果如圖5所示。

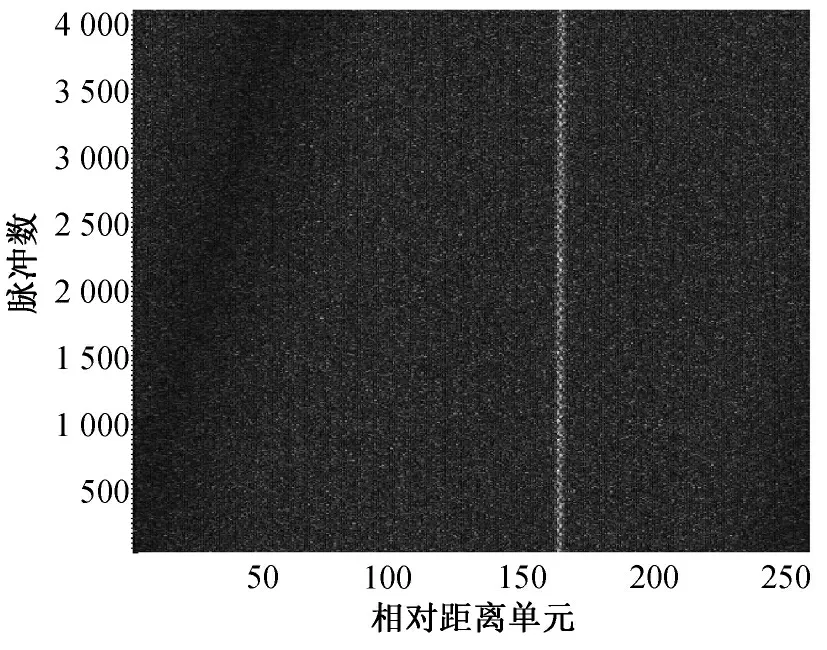
圖5 Keystone變換后的包絡

包絡對齊之后，由于加速度的影響使多普勒相位不為線性，直接FFT 操作出現跨多普勒單元現象，如圖6所示。

采用Dechirp方法對加速度進行搜索補償，使多普勒相位線性變化，直接FFT 實現相參積累，結果如圖7所示。

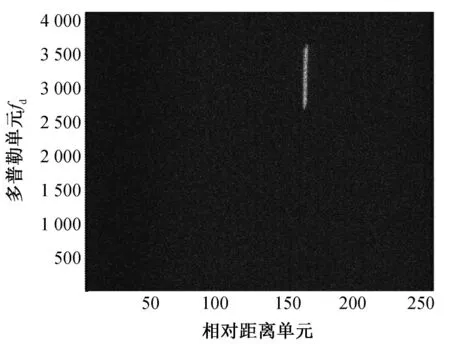
圖6 包絡校正后直接FFT 結果

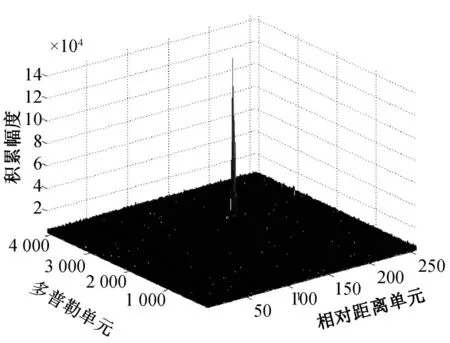
圖7 距離和多普勒補償后相參積累結果

從圖中可以看出，通過本文的方法，積累幅度得到較大提高。

對不同輸入SNR 進行1 000次Monte Carlo實驗，實驗結果如圖8所示。仿真中MTD 的脈沖積累個數為不出現距離和多普勒走動的最大積累個數為75。

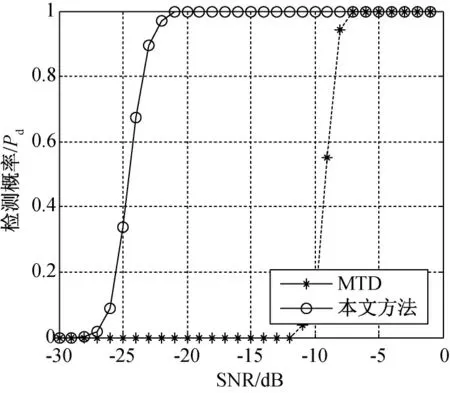
圖8 虛警概率10-6時目標檢測概率曲線

從圖中可以看出，在虛警率為10-6，檢測概率為0.8時，采用本文方法將目標的最小可檢測SNR 比MTD 方法提高約15dB，檢測性能顯著提高。

4 結束語

本文針對長時間相參積累過程中出現的距離走動和多普勒擴散問題，提出結合Keystone變換和Dechirp方法進行距離走動校正和多普勒擴散進行補償。最后通過仿真實驗表明，本文方法能夠顯著提高積累增益和檢測性能。

［1］ 保錚.雷達信號的長時間積累.第七屆中國雷達學術年會論文集［C］.南京：中國電子學會，1999.

［2］ Carlson B D，Evans E D，Wilson S L.Search Radar Detection and Track with the Hough Transform，Part I：System Concept［J］.IEEE Transactions on Aerospace and Electronic Systems，1994，30（1）：102-108.

［3］ 張順生，曾濤.基于keystone 變換的微弱目標檢測［J］.電子學報，2005，33（6）：1675-1678.

［4］ 王娟，趙永波.一種改進的Keystone變換算法及其在微弱信號檢測中的應用［J］.航空兵器，2011，（5）：3-6.

［5］ 趙永波，周曉佩.一種用于微弱信號檢測的廣義Keystone變換算法［J］.西安電子科技大學學報，2013，40（2）：120-125.

［6］ 劉建成，王雪松，劉忠，等.基于Wigner-Hough變換的LFM 信號檢測性能分析［J］.電子學報，2007，36（6）：1212-1216.

［7］ 齊林，陶然，周思永，等.基于分數階Fourier變換的多分量信號的檢測和參數估計［J］.中國科學，2003，33（8）：749-759.

［8］ Xia X G.A Quantitative Analysis of SNR in the Short-time Fourier Transform Domain for Multi-Component Signals ［J］.IEEE Transactions on Signal Processing，1998，46（1）：200-203.