地空鏈路雨衰減預測模式研究

趙振維 盧昌勝 林樂科 張 鑫 李 磊 吳振森

(1．中國電波傳播研究所電波環境特性及模化技術重點實驗室,山東 青島 266107;2．西安電子科技大學理學院,陜西 西安 710071)

引 言

Ku頻段衛星通信、廣播等系統已得到廣泛的應用，Ka頻段及其更高頻段的衛星系統正在快速發展，此外，Ka頻段深空探測和空間飛行器測控等應用系統中得到越來越廣泛的應用，而雨衰減是影響工作在10 GHz以上頻段無線電信息系統性能的關鍵因素之一，是系統鏈路可靠性設計的重要依據.因此提高雨衰減的預測精度對提高系統的設計可靠性和抗衰落能力至關重要，因此長期以來國際上進行了大量理論和實驗研究，建立了一系列地空鏈路雨衰減預測模式和方法[1-11].到目前為止，絕大部分雨衰減預測模式在采用觀測點降雨率的基礎上對傳播路徑進行等效，如路徑調整因子或路徑縮短因子法[1-6].為了提高雨衰減的預報精度，我們建立了基于指數雨胞的雨衰減物理模型[12]，在此基礎上通過進一步的理論分析，提出了降雨率調整因子的概念，利用這一物理模型和降雨率調整因子可以更好的解釋雨衰減實驗數據的特性[13].雨衰減的預測通常采用兩種方法，一種為概率轉換方法，即先通過0.01%時間概率的降雨率預測0.01%時間概率的雨衰減，再通過概率轉換公式得到其他時間概率的雨衰減；另一種是利用全概率降雨率分布的雨衰減預報方法，該方法直接利用降雨率分布中不同時間概率降雨率直接預測相應概率的雨衰減.目前利用全概率降雨率分布的衰減預測模式已成為雨衰減預測模式的研究重點和發展趨勢.

在地空鏈路雨衰減預測中，一般認為，鏈路仰角越低，電波穿越雨區的路徑越長，雨衰減越大.隨著傳播仰角的增大，電波穿過雨區的距離減小，此時降雨造成的衰減也應隨之降低，也就是說雨衰減隨仰角的增加應單調遞減.但是，2003年在巴西提交國際電聯的文稿中指出ITU-R地空鏈路雨衰減預測模式[14]的預測結果在仰角由小到大變化時雨衰減預測值先減小后增大[14]，被稱為雨衰減模式預測的奇異現象.本文進一步分析了近年來中國[15]、巴西[16]和英國[17]提交國際電聯的地空鏈路雨衰減模式，發現同樣存在這一奇異現象.利用 ITU-R地空鏈路雨衰減實驗數據，分析了造成各地空鏈路雨衰減預測模式預測出現奇異現象的原因.基于指數雨胞模型的雨衰減物理模型提出的降雨率調整因子的概念，由ITU-R地空鏈路雨衰減數據回歸得到了降雨率調整因子公式的參數，建立了一種利用全概率降雨率分布的地空鏈路雨衰減預測模式.與前述的地空鏈路雨衰減模式比較表明，這一模式預測精度優于其它地鏈路雨衰減預測模式，形式更加簡單，且消除了模式預測的奇異性，有效提高了模式預測的可靠性.

1 地空鏈路雨衰減建模方法及其預測奇異性分析

地空鏈路降雨傳播如圖1所示，與地面視距鏈路雨衰減預測模式建模方法類似[19]，地空鏈路雨衰減模式通常也采用路徑調整因子的概念獲得等效路徑長度，并通過下式進行雨衰減預測.

A=γRLE=kRαLSδ,

(1)

式中：γR(dB/km)為雨衰減率，由ITU-R P. 838-3建議給出[20]；LE(km)為等效路徑長度；LS(km)為電波傳播路徑長度；δ為路徑調整因子.

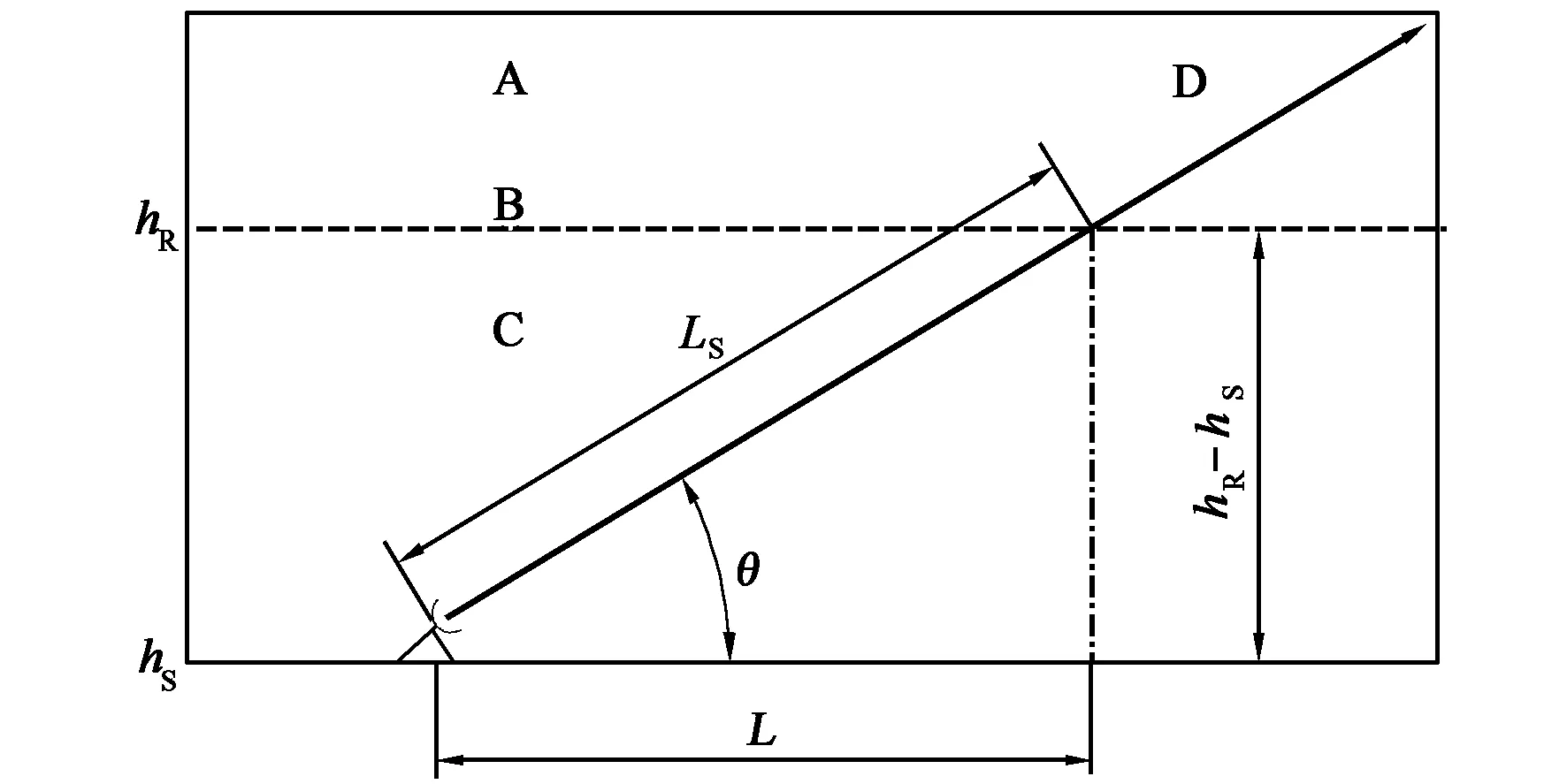
圖1 地空傳播路徑示意圖(A區：冰凍水凝物區；B：雨頂高度，C區：降雨區；D：地空路徑)

圖1中hR(km)和hs(km)分別為雨頂高度和站點海拔高度，θ(度)為地空鏈路傳播仰角.

ITU-R地空鏈路雨衰減預測模式[6]作為國際標準模式得到了廣泛應用.其通過0.01%時間概率的降雨率先預測0.01%時間概率的雨衰減，再通過概率轉換公式得到其他時間概率的雨衰減.這一模式既考慮了降雨的水平不均勻性，也考慮了降雨的垂直不均勻性，并利用水平調整因子η0.01和垂直調整因子υ0.01表示為

(2)

(3)

式中：f(GHz)為頻率；LG=LScosθ(km)為傳播路徑的水平投影.上式中LR和χ由以下過程計算得到：

(4)

若ζ>θ：

(5)

否則：

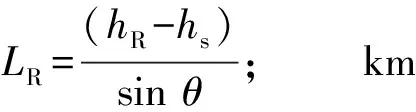
(6)

φ(度)為地面站緯度，若|φ|<36°，

χ=36-|φ| ； degrees

(7)

否則：

χ=0； degrees

(8)

由此得到等效路徑長度：

LE=LRυ0.01. km

(9)

可由式(1)計算0.01%時間概率被超過的雨衰減A0.01，并由下式轉換得到0.001%～5%時間概率的雨衰減為

(10)

式中若p≥1%或|φ|≥36°β=0 ；若p≤1%和|φ|≥36°且θ≥25°，β=-0.005(|φ|-36)；其他：

β=-0.005(|φ|-36)+1.8-4.25sinθdB .

(11)

我們曾建立了一種采用單一路徑調整因子的地空鏈路雨衰減預測模式，并由2005年提交國際電聯(China2005模式)[15]，其0.01%時間概率路徑調整因子為δ0.01：

-1.64(1-exp(-2.06LG))].

(12)

由式(1)計算0.01%時間概率被超過的雨衰減A0.01，并由下式轉換得到0.001%～5%時間概率的雨衰減為

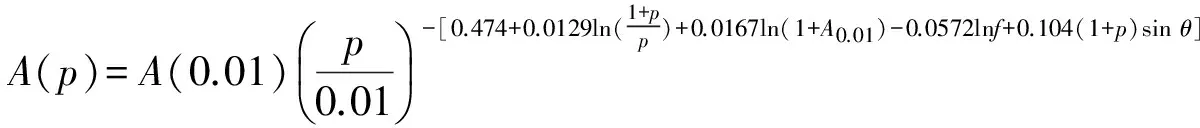
(13)

英國在2003年提交國際電聯的文稿中提出了一種利用全概率降雨率分布的地空鏈路雨衰減預報模式(UK模式)[17]，其同樣考慮了降雨的水平不均勻性和垂直不均勻性，并利用與其提出的地面視距雨衰減模式相同的水平調整因子η(p)和一個新的垂直路徑調整因子ν(p)為

(14)

ν(p)= min{2,1.67+[4.47(hR-hs)-4.6

-0.46]logR(p)}，

(15)

式中R(p)(mm/h)為p%時間概率的降雨率,當R(p)小于1時其值取1，相應的雨衰減計算公式為

A(p) =γR(p)·LE(p)

=γR(p)·LS·η(p)·ν(p) . dB

(16)

巴西的L. da Silva Mello等為了提高地空鏈路雨衰減的預測精度，在使用路徑縮短因子的同時，引入了垂直和水平等效降雨率的概念.當仰角為0時，可轉化為其提出的地面視距鏈路雨衰減預測模式.這一模式由巴西提交到國際電聯(Brazil模式)[16]，該模式為

(17)

式中Reff為等效降雨率；

Reff=Reff1+Reff2;

Reff1=1.763R0.753+0.197/LScos θcosθ；

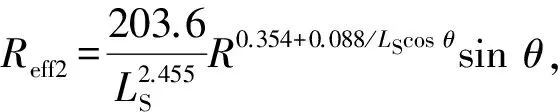
由于地空鏈路隨著傳播仰角的增大，電波經過雨區的長度變短，雨衰減應隨仰角的增加而單調減小.巴西提交國際電聯的文稿[14]表明，當利用ITU-R雨衰減預測模式預測相同降雨率，不同仰角的降雨衰減時預測結果隨仰角的單調遞增出現了非單調遞減的奇異性現象，即其隨仰角由小到大變化時其雨衰減預測結果先遞減而后遞增，出現如圖2所示的情況.

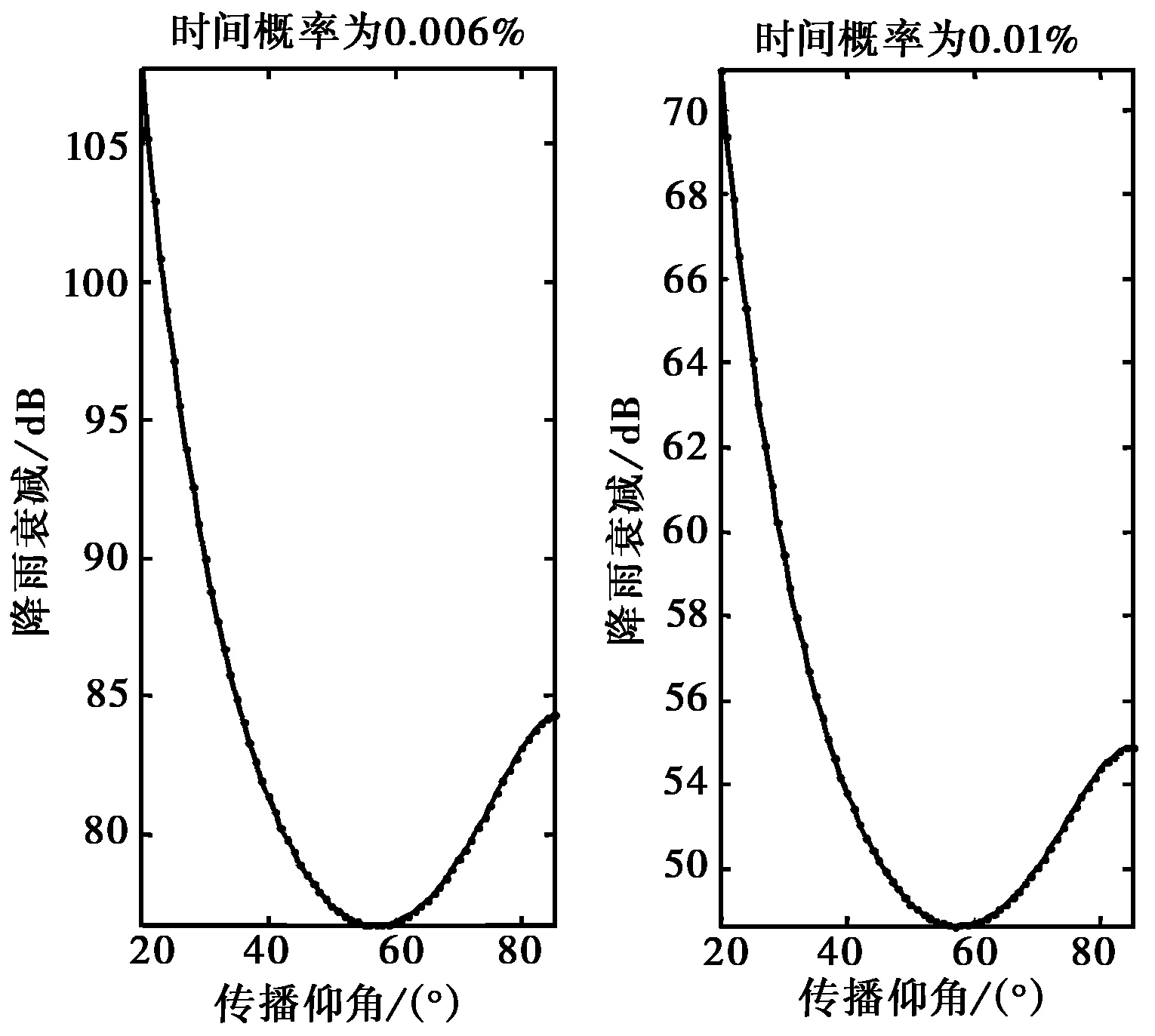
圖2 ITU-R模式雨衰減與仰角的分布關系(頻率為30 GHz)

為了檢驗其他模式是否同樣存在預測的奇異性，我們分析了上述China2005模式、UK模式和Brazil模式，其結果如圖3所示.從圖中可以看出，上述模式同樣存在預測的奇異性.

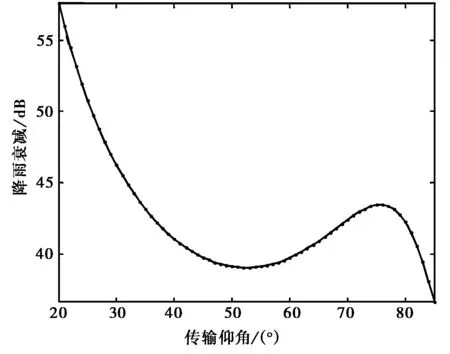
(a) China2005模式

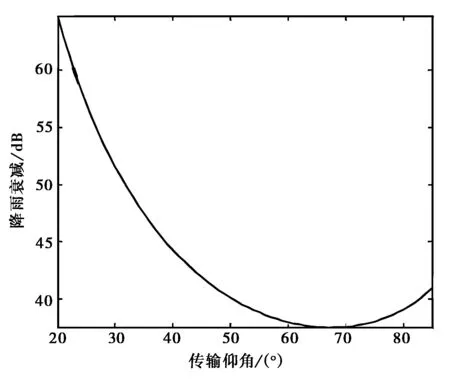
(b) UK模式

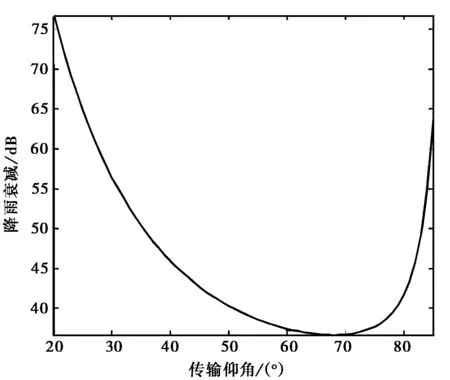
(c) Brazil模式圖3 各模式預測雨衰減隨仰角的變化(頻率為30 GHz，降雨率為59mm/h)

由于上述雨衰減預測模式均是半經驗模式，模式參數由實測雨衰減數據確定.全球大部分地空鏈路雨衰減數據是由歐美國家在中高緯地區測量得到的[21]，而高仰角的低緯地區測量數據很少，在模式參數確定中的權重較小，無法反映模式對高仰角的適用性，因此，國際上對模式預測奇異性是由建模不合理導致的，還是降雨空間分布導致的固有雨衰減傳播特征還未給出合理的解釋.為了確定這種降雨衰減隨傳輸仰角的奇異性變化是否為降雨空間分布導致的固有雨衰減傳播特征，利用對ITU-R雨衰減試驗數據[22]對雨衰減隨仰角變化特性進行分析.利用雨衰減數據和式(1)得到實際的等效路徑長度：

(18)

假設雨頂高度相同，則等效路徑長度隨仰角的變化和雨衰減隨仰角變化的趨勢是相同的，利用式(18)和ITU-R試驗數據庫數據[22]得到等效路徑長度與傳播仰角的分布圖，如圖4所示.

從圖4中可以看出由ITU-R實驗數據得到的實測等效路徑長度并未出現上述模式預測中的奇異現象，總體趨勢隨傳播仰角的增大而單調減小，因此，相應的降雨衰減也應隨仰角的增大而單調減小.由此可以看出，造成雨衰減模式結果隨仰角變化的奇異性現象應是模式本身造成的.由于現有ITU-R地空鏈路雨衰減預測模式的奇異性，利用其預測高仰角地區雨衰減是不適用的.

圖4 等效路徑長度與降雨率、傳播仰角關系

2 地空鏈路雨衰減預測模式研究

為了建立更符合物理基礎的雨衰減預測模式，我們建立了一種基于指數雨胞的雨衰減物理模型[12]，如圖5所示，并在此基礎上通過進一步的理論分析，提出了降雨率調整因子的概念，由此雨衰減可由(1)式表示，且基于指數雨胞的雨衰減物理模型導出的降雨率調整因子可解釋雨衰減實驗數據的主要特征[13].

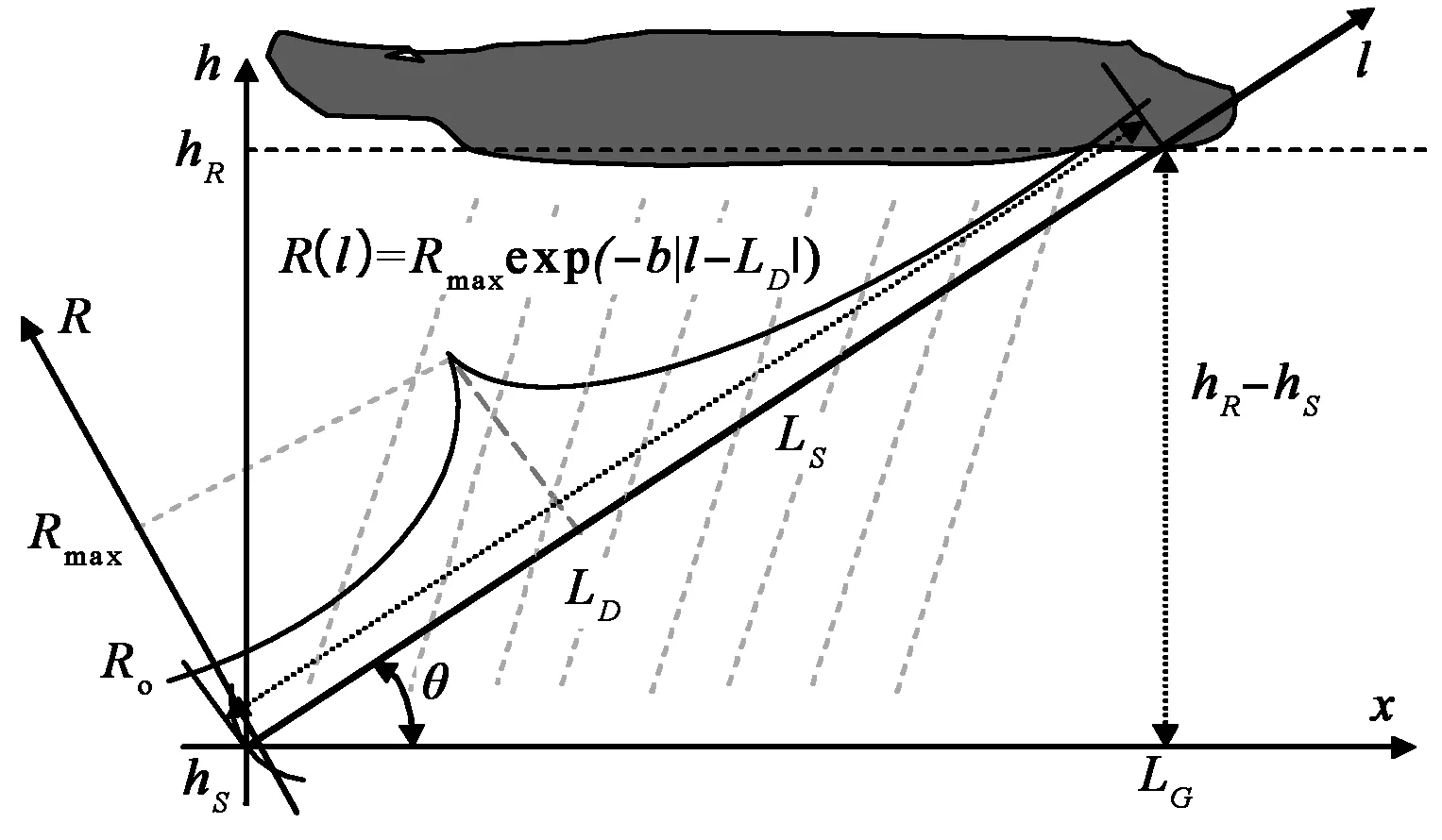
圖5 指數雨胞應用于地空鏈路中

文獻[13]給出的地面視距鏈路和地空鏈路雨衰減的統一預測模式為

A(p)=k[r(p)·R(p)]αLS,

(19)

式中r(p)為降雨率調整因子.為了確定降雨率調整因子的函數形式，利用和文獻[18]中分析地面視距鏈路相似的方法，基于ITU-R地空鏈路雨衰減實驗數據[21]，對降雨率調整因子與降雨率、傳播路徑長度和時間概率等進行分析.圖6給出了不同路徑長度下，降雨率調整因子與降雨率的關系，圖7給出了不同時間概率下降雨率調整因子與路徑長度的關系.

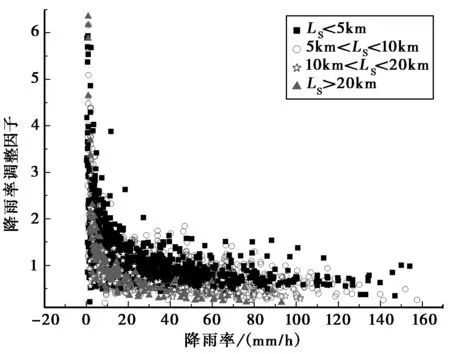
圖6 降雨率調整因子隨降雨率的變化

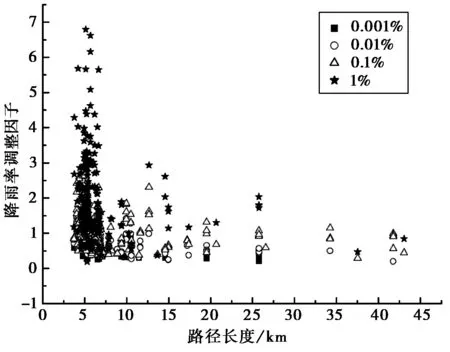
圖7 降雨率調整因子隨路徑長度的變化

從圖6和圖7可以看出地空鏈路降雨率調整因子與降雨率、路徑長度以及時間概率的關系與地面視距鏈路具有很相似特征.同時為了考慮地空鏈路雨衰減與傳播仰角的關系，利用ITU-R數據庫地空鏈路雨衰減實驗數據[21]得到的降雨率調整因子與傳播仰角的關系如圖8所示.

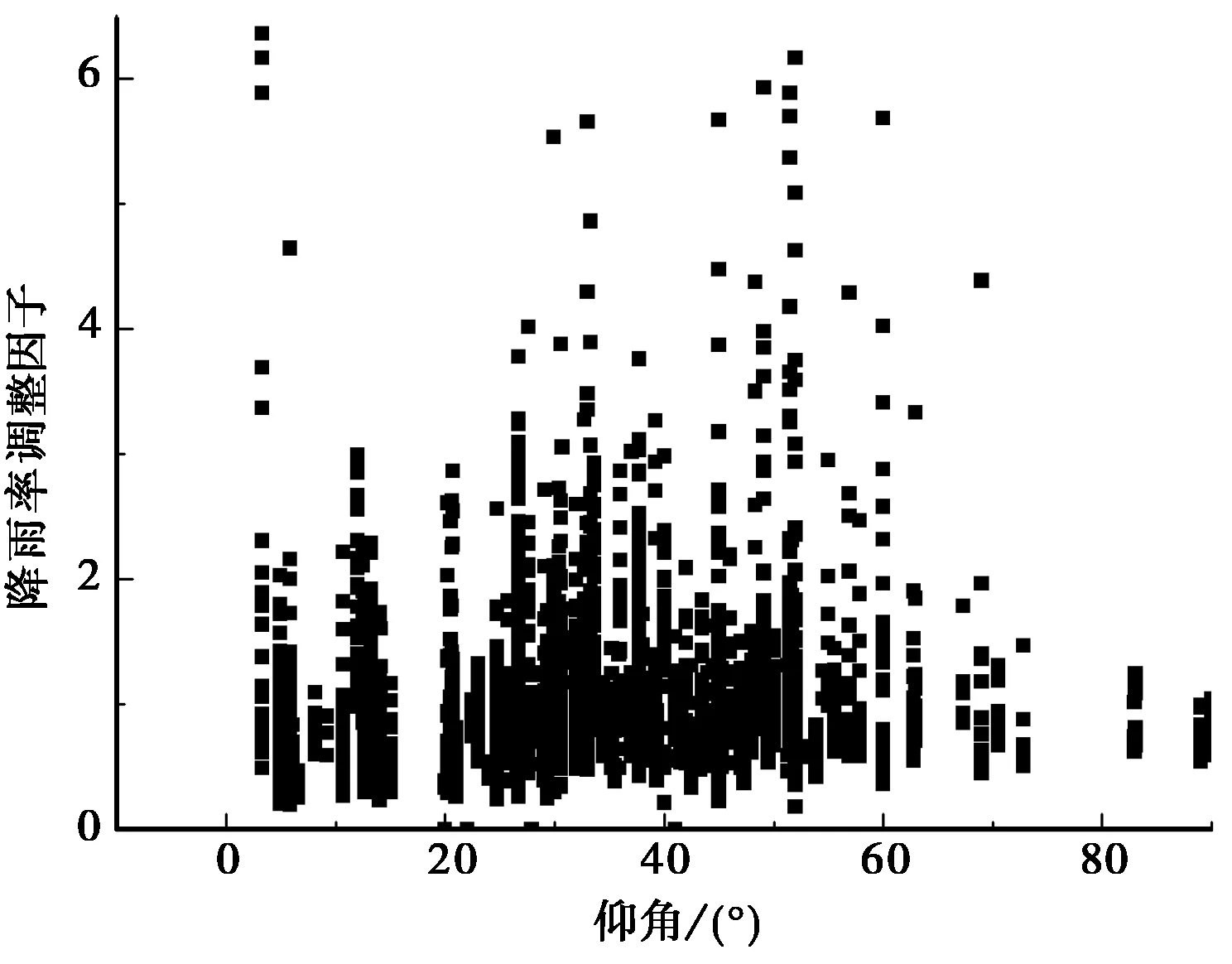
圖8 降雨率調整因子隨仰角的變化

從圖8中可以看出降雨率調整因子與仰角不存在明顯的變化關系.因此，地空鏈路雨衰減預測模式可采用和地面視距鏈路形式相同的降雨率調整因子函數形式[18]，即：

(20)

3 模式比較

3.1 參數擬合及模式比較準則

按ITU-R P.311建議[22]對各模式進行誤差分析，該建議采用預測衰減值與測量衰減值之比的對數作檢驗變量.其誤差計算公式為

(21)

式中Am表示測量值，Ap表示預測值.在測量雨衰減小于10 dB時，上式中有一個的補償修正因子(Am/10)0.2，它是為了補償較低測量衰減值的不精確以及雨衰減之外的損耗(如閃爍衰落、大氣衰減等)而引進的.對于地空鏈路取13個時間概率點(時間百分比：0.001，0.002，0.003，0.005，0.01，0.02，0.03，0.05，0.1，0.2，0.3，0.5，1)進行比較.同時考慮權年因素，即如果測試數據是兩年累計結果，按兩組數據計算，權年數為2.通過這種檢驗，可以得到各種模式在不同時間百分數上的平均誤差、均方根誤差及標準偏差等.通過比較，均方根誤差(RMS)最小的預測模式，認為其預測精度最高.

利用上述方法和改進CHC遺傳算法結合模擬退火算法以及ITU-R雨衰減數據[17]對系數a1-6進行優化、回歸，當得到均方根誤差最小時對應的參數為最終結果.由此獲得地空鏈路雨衰減預測模式中的降雨率調整因子為

(22)

可由式(19)根據降雨率統計分布預測雨衰減的統計分布.因此，這一預測模式是一種利用全概率降雨率分布的雨衰減預測模式.

3.2 模式比較

根據ITU-R P.311建議[22]對ITU-R模式[6]、UK模式[17]、Brazil模式[16]、China2005模式[15]和本文模式進行比較.各模式整體比較結果如表1所示.圖9～圖11給出了各模式在不同時間概率點上的均值誤差、均方根誤差以及標準偏差的比較結果.

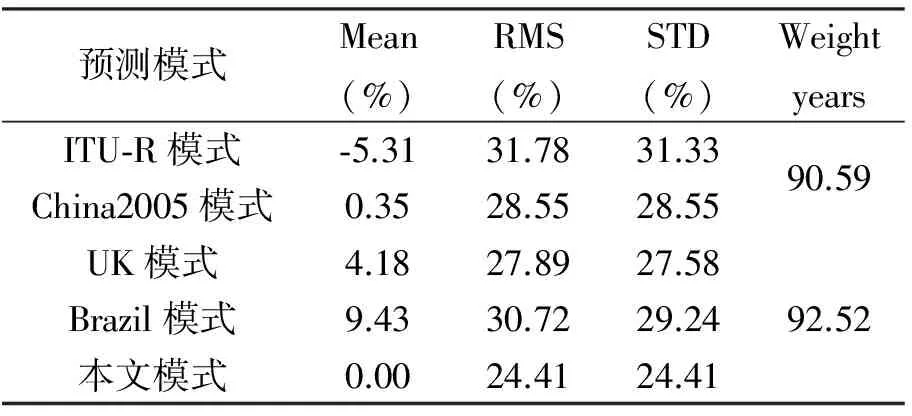
表1 各模式預測結果比較

從表1的整體比較可以看出，本文模式較其它模式在均值誤差、均方根誤差以及標準偏差三方面都有較大的改進.由圖9～圖11也可以看出，本文模式在不同時間概率點均能得到較ITU-R和其它模式更好的預測精度.

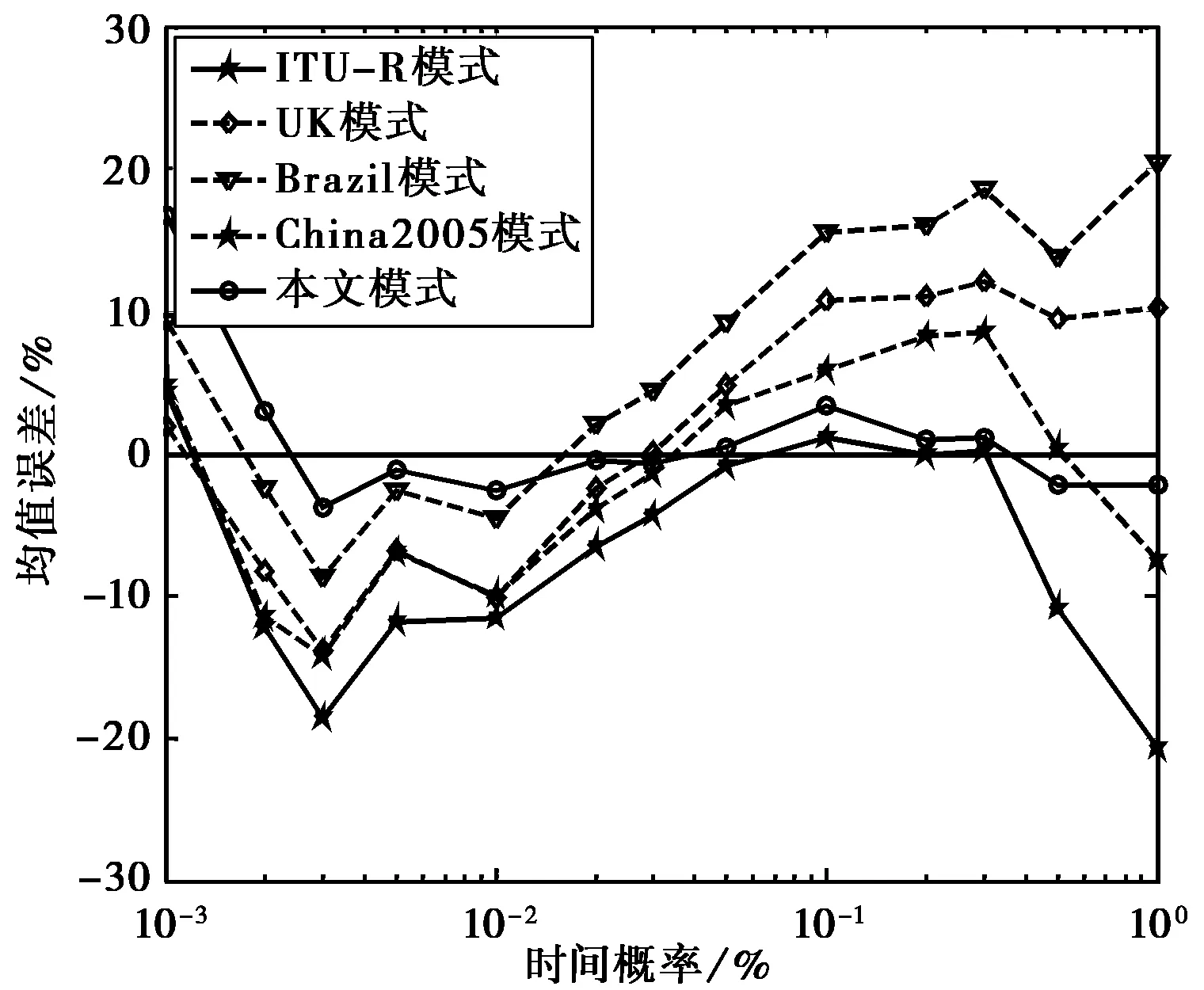
圖9 模式均值誤差比較

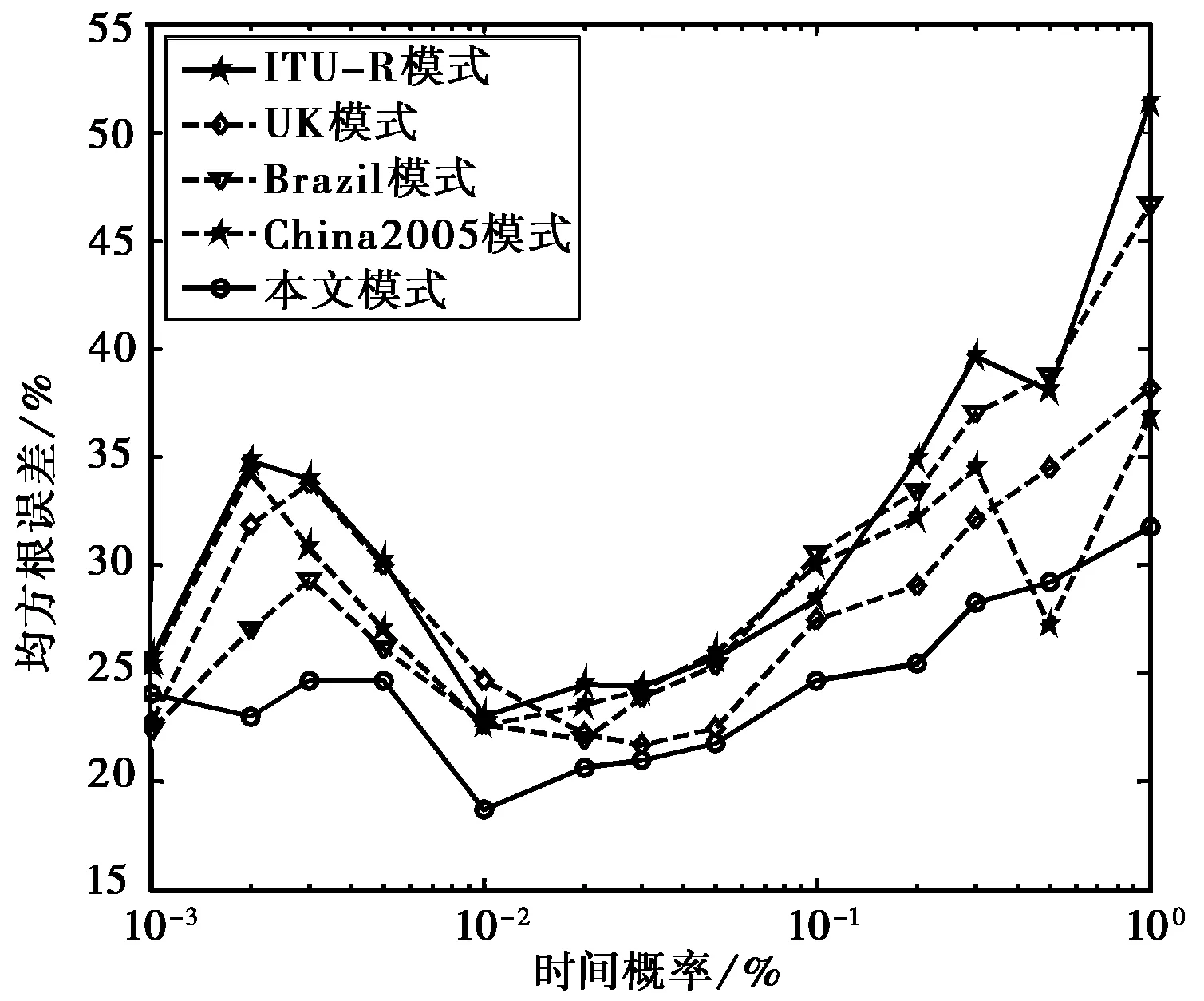
圖10 模式均方根誤差比較

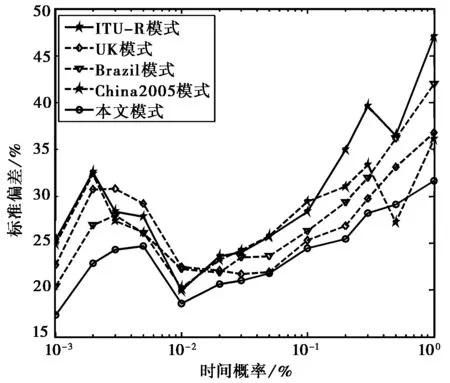
圖11 模式標準偏差比較

對于同步衛星來說，高仰角鏈路通常位于低緯度地區，因此為了檢驗新模式是否在高仰角下的預測精度有所改善，對各模式在低緯度地區(緯度小于36度)的預測精度進行比較，如圖12所示.結果表明本文模式的預測精度較其他模式均有較大的改善.

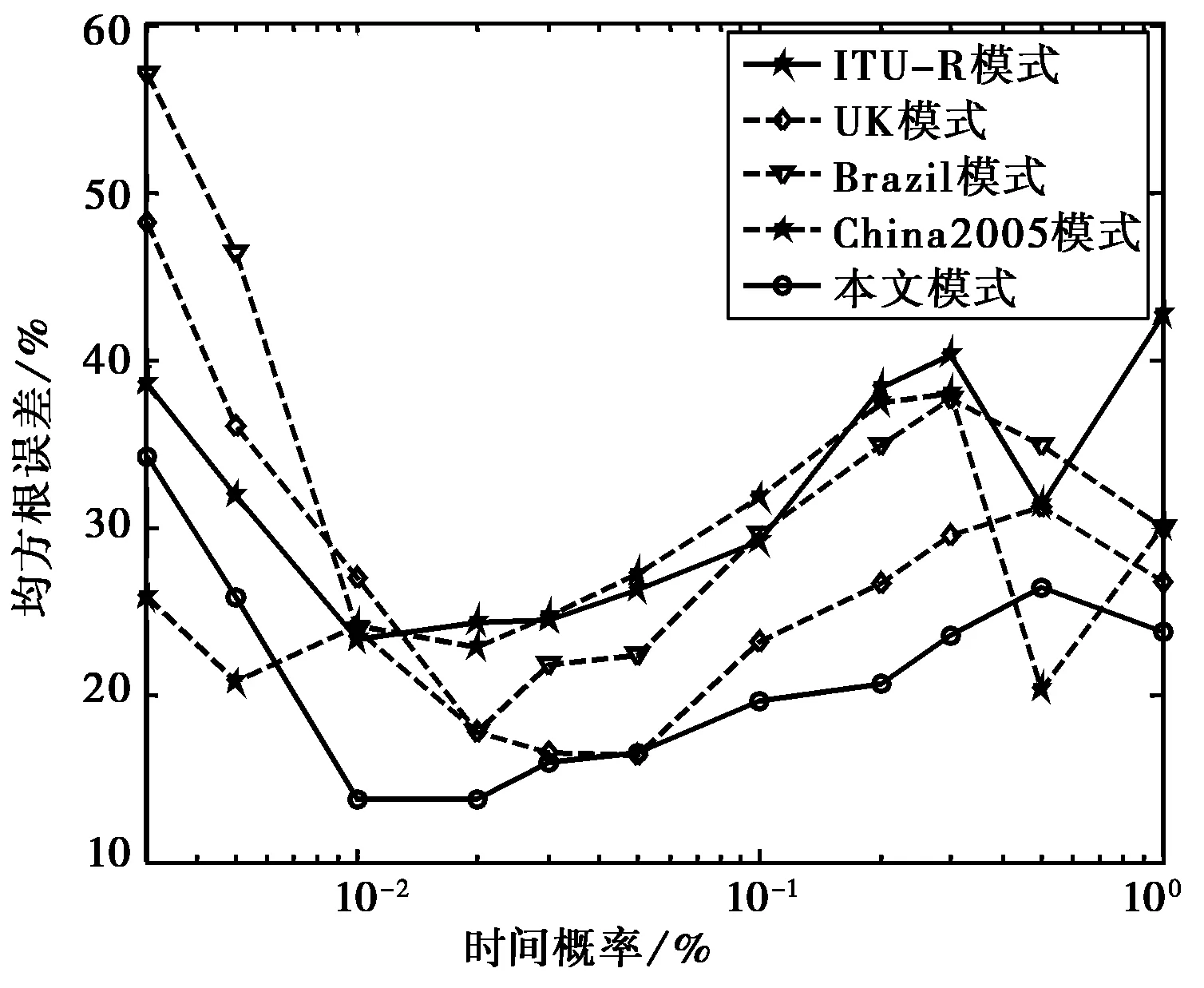
圖12 低緯地區均值誤差比較

本文模式在不同降雨率和不同頻率時預測結果隨仰角的變化如下圖13所示.

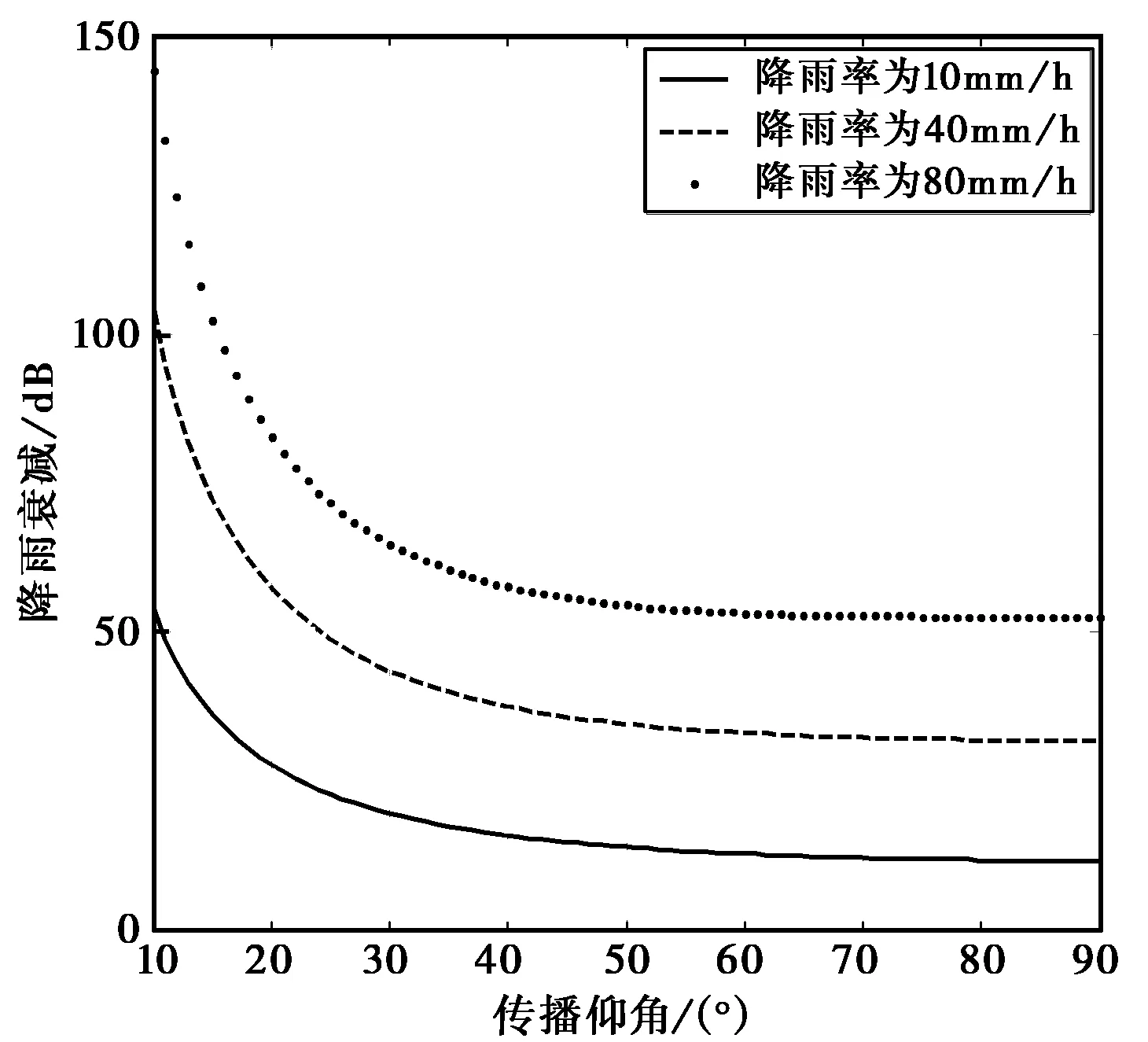
(a) 不同降雨率(頻率為30 GHz)

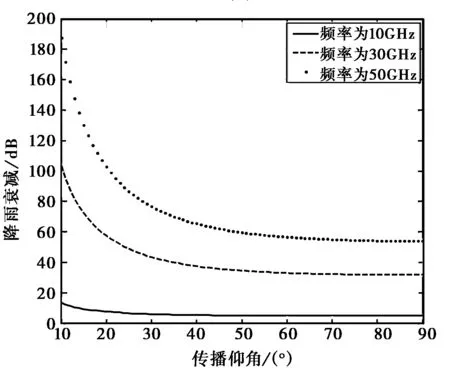
(b) 不同工作頻率(降雨率60 mm/h)圖13 本文模式獲得的等效路徑長度

從圖13可以看出本文模式預測的雨衰減隨傳播仰角的增大而單調較小，不存在隨仰角奇異性現象.

4 結 論

本文利用ITU-R數據庫地空鏈路雨衰減實驗數據，系統分析ITU-R地空鏈路雨衰減模式和其它幾種模式存在的預測雨衰減隨仰角增大，非單調減小的奇異現象.分析表明實驗數據并未表現出奇異現象，因此，模式預測的奇異性是不正確的.在此基礎上，利用基于指數雨胞模型的雨衰減物理模型得到的降雨率調整因子和ITU-R數據庫地空鏈路雨衰減實驗數據，得到了地空鏈路雨衰減預測降雨率調整因子公式的參數，建立了一種利用全概率降雨率分布的地空鏈路雨衰減預測模式.通過與ITU-R模式、China2005模式、UK模式和Brazil模式的比較表明，本文模式預測精度較ITU-R模式和其它模式均有提高，且模式形式與地面視距鏈路雨衰減預測模式相同，預測過程更加簡便，具有更好的物理基礎，因此該模式可替代ITU-R地空鏈路雨衰減預測模式，用于各種天基無線電系統的設計.

[1] FLAVIN R K. Satellite Link Rain Attenuation in Brisbane and a Proposed New Model for Australia[R]. Telstra Research Laboratories, 1996.

[3] MATRICCIANI E. Rain attenuation predicted with two-layer rain model[J]. European Transactions on Telecommunication, 1991, 2(6): 715-727.

[4] STUTZMAN W L, DISHMAN W K. A simple model for the estimation of rain-induced attenuation along earth-space paths at millimeter wavelengths[J]. Radio Science, 1982, 17(6): 1465-1476.

[5] 李煥矩. 地空路徑雨衰減的預報研究[J].電波科學學報, 1990, 5(3): 1-7.

LI Huanju. On the prediction of rain attenuation for earth-space propagation paths[J]. Chinese Journal of Radio Science, 1990, 5(3):1-7. (in Chinese)

[6] ITU-R. Recommendation P.618-10 'Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems'[S]. Geneva: International Telecommunication Union, 2009.

[7] FISER O. Interaction of Electromagnetic Field with Rain Medium with Respect to Satellite Links Rain Attenuation Prediction in Frequency Range above 10 GHz[D]. Prague: CTU Prague, 1986.

[8] CAPSONI C, FEDI F, MAGISTRONI C, et al. Data and theory for a new model of the horizontal structure of rain cells for propagation applications[J]. Radio Science, 1987, 22(3): 395-404.

[9] CRANE R K. A two-component rain model for the prediction of attenuation statistics[J]. Radio Science, 1982, 17(6): 1371-1387.

[10] CAPSONI C, FEDI F. Data and theory for a new model of the horizontal structure of rain cells for propagation applications[J]. Radio Science, 1987, 22(3): 395-404.

[11] BRYANT G F. Rain attenuation statistics from rain cell diameters and heights[J]. International Journal of Satellite Communications, 2001, 19: 263-286.

[12] 趙振維, 盧昌勝, 林樂科, 等. 基于雨胞分布的視距鏈路雨衰減預報模型[J].電波科學學報, 2009, 24(4): 627-631.

ZHAO Zhenwei, LU Changsheng, LIN Leke, et al. Prediction model of rain attenuation based on the EXCELL rain cell model for the terrestrial line-of-sight systems[J]. Chinese Journal of Radio Science, 2009, 24(4): 627-631.(in Chinese)

[13] 趙振維, 盧昌勝, 林樂科, 等. 雨衰減預測中的降雨率調整因子概念[J].電波科學學報, 2013, 28(1): 33-38.

ZHAO Zhenwei, LU Changsheng, LIN Leke, et al. The conception of rainfall adjustment factor for the rain attenuation prediction[J]. Chinese Journal of Radio Science, 2013, 28(1): 33-38.(in Chinese)

[14] ITU-R. Document 3M/17, Comments on Recommendation ITU-R P.618-7 Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems[R], 2003.

[15] ITU-R. Document 3M/108, Proposed Modification to Recommendation ITU-R P.618-8: the Prediction Method of Rain Attenuation along Earth-Space Path[R], 2005.

[16] DA SILVA MELLO L, PONTES M S. Unified Method for the Prediction of Rain Attenuation in Satellite and Terrestrial Links[J]. Journal of Microwaves, Optoelectronics and Electromagnetic Applications, 2012, 11(1): 1-14.

[17] ITU-R. Document 3M/28, Proposed Modification to Recommendation ITU-R P.618-8: Propagation Data and Prediction Methods Required for the Design of Earth-Space Telecommunication Systems[R], 2003.

[18] 盧昌勝, 趙振維, 林樂科, 等. 一種地面視距鏈路雨衰減預測模式[J].電波科學學報,2013, 28(2): 272-277.

ZHAO Zhenwei, LU Changsheng, LIN Leke, et al. A prediction model of rain attenuation for the terrestrial line-of-sight links[J]. Chinese Journal of Radio Science, 2013, 28(2): 272-277. (in Chinese)

[19] ITU-R Recommendation P.530-14 'Propagation Data and Prediction Methods Required for the Design of Terrestrial Line-of-sight Systems'[R]. Geneva: International Telecommunication Union, 2011.

[20] ITU-R. Recommendation P.838-3 'Specific Attenuation Model for Rain for Use in Prediction Methods'[S]. Geneva: International Telecommunication Union, 2006.

[21] ITU-R. Recommendation ITU-R P.837-4, 'Characteristics of Precipitation Modeling'[S]. Geneva: International Telecommunication Union, 2003.

[22] ITU-R new database on earth-satellite. [DB/OL]. [2012-06-28] http://saruman.estec.esa.nl/dbsg3/categories.jsp?category=annualRainAttStat.

[23] ITU-R. Recommendation P.311-13: 'Acquisition, Presentation and Analysis of Data in Studies of Tropospheric Propagation'[S]. Geneva: International Telecommunication Union, 2009.

[24] 林樂科. 對流層環境對地空傳播特性影響研究[D]. 北京: 電子科學研究院, 2004.

LIN Leke. Influence of Troposphere on Radio Propagation on Earth-Space Paths[D]. Beijing: China Electronic Science Research Institute, 2004.(in Chinese)