一種基于Walsh矩陣的正交多相碼設計方法

李 軍 劉 娜 劉紅明 孫 穎 何子述

(電子科技大學電子工程學院，四川 成都 611731)

引 言

正交信號一般應用于多輸入多輸出(Multiple-Input Multiple-Output, MIMO)雷達體系[1-3]，良好的正交波形能夠在空間上形成低增益的寬波束，提高雷達的抗截獲性能. 接收信號經過數字多波束技術后，能夠形成多個高增益的窄波束，能夠同時檢測出多個目標.總之，正交波形的設計越來越受到人們的重視.

常見正交波形的信號形式有正交離散頻率編碼信號[4]、正交頻分復用-線性調頻信號[5]、正交多相編碼信號[6].由于正交多相編碼信號帶寬利用率高，本文從多相碼設計角度對正交波形進行設計.目前正交相位編碼信號設計方法多集中在智能領域中，如Liu等[7]利用遺傳算法進行正交性的搜索和相關量的優化，但是這種算法很容易陷入局部最優.針對這一現象，Deng[8]利用基于遺傳算法的模擬退火算法進行了正交相位編碼信號的設計，這一設計雖然具有很強的局部搜索能力，但是卻對整個搜索空間不夠了解，不利于將搜索過程進入最希望的區域，而且沒有解決在目標零偏移點處，信號間嚴格正交性(后文將在目標零點偏移處信號間嚴格正交性簡稱嚴格正交性)的問題，這將會直接影響到雷達的角度測量精度和雜波對消效果[9-10].為了解決相位編碼信號間嚴格正交性的問題[11]，本文引入了Walsh函數的概念，提出了一種基于Walsh矩陣的正交多相碼信號設計方法.Walsh矩陣保證信號間具有嚴格正交性，通過對Walsh矩陣列變換，為遺傳算法提供了嚴格正交性空間域，使得遺傳算法優化速度得到了很大的提升.同時在遺傳算法中添加了“和信號”形式的代價函數，使得設計出的信號組在目標檢測性能上得到了提升.“和信號”的概念來源于每個接收信號是所有發射信號在空間上疊加后的綜合信號，因此對接收的“和信號”做相關處理時，要求所有發射信號都與“和信號”做匹配濾波，各匹配濾波后疊加的綜合輸出旁瓣量直接決定著雷達對目標的檢測性能，根據這一理念才把“和信號”的相關旁瓣輸出增加為遺傳算法代價函數之一.

本設計方案是在保證信號間嚴格正交性的同時，盡可能地降低“和信號”相關峰值旁瓣量、自相關峰值旁瓣量以及互相關峰值量.嚴格正交性的保證是通過變化后的類Walsh矩陣給予的，類Walsh矩陣是通過Walsh矩陣變化重組生成的正交多相碼矩陣，Walsh矩陣則是通過Walsh函數采樣得到的.低相關旁瓣量則是通過遺傳算法對嚴格正交信號空間域進行篩選實現的.嚴格正交性使得信號處理時具有更優的角度測量精度和雜波對消效果；低自相關旁瓣量和低互相關量的設計使得發射信號組在空間上能量分布均勻，同時降低了信號間的干擾，便于隱身；低“和信號”相關峰值旁瓣量的設計使得雷達綜合輸出端有更好的目標檢測概率；多相碼的設計使得信號更不容易被破獲且能夠獲得比較低的相關旁瓣量.

1 正交多相碼信號形式

假設MIMO雷達發射的是一組正交相位編碼信號，信號個數為L，每個信號的編碼長度為N，那么編碼信號集合可表示如下：

{Sl(t)=a(t)ejφl(n),n=1,2,…,N},l=1,2,…,L，

(1)

且為了滿足信號間嚴格正交性，要求任意兩個信號間滿足關系為

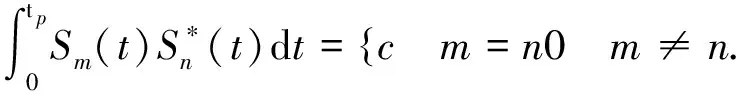
(2)

式中：a(t)為每個碼元的載頻信號；tp為信號持續時間；φl(n)為第l個信號第n個碼元內信號的初始相位，對于四相碼來說相位取值為

φl(n)∈{0,π/2,π,3π/2}.

(3)

根據信號的相關處理特性，可以定義自相關A(φl,k)序列、互相關C(φp,φq,k)序列，“和信號”相關S(k)序列表達式為

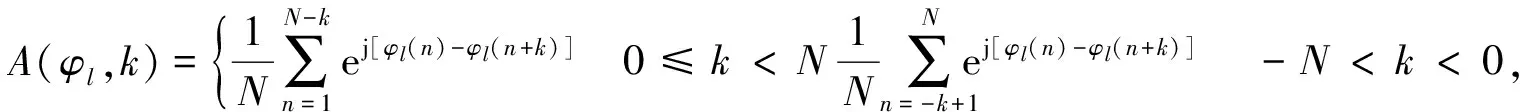
(4)

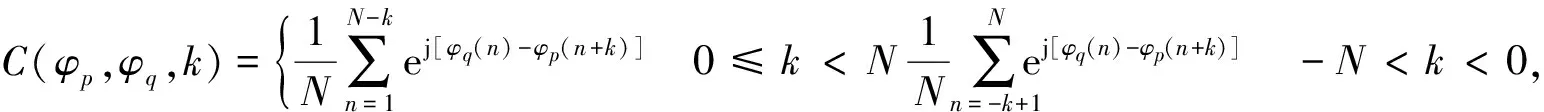
(5)

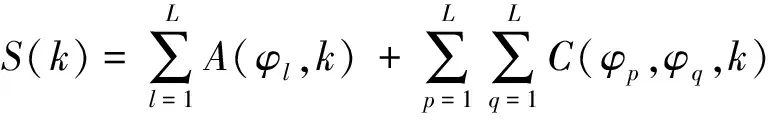
(6)

由于載頻信號在每個碼元中保持不變，因此在計算相關量時可以不做考慮，簡化了計算復雜度.由式(4)、(5)和(6)可見相關輸出是一個滑動相關的過程，旁瓣輸出是不可避免的.“和信號”相關峰值旁瓣量高將會直接引起虛假目標的產生或者掩蓋了真實的弱目標，高的自相關旁瓣量和互相關量則會使得發射信號組在空間上能量分布不均勻，不利于隱身，所以要求設計出的正交相位編碼信號具有三種類型的低旁瓣量.

2 基于Walsh矩陣的正交多相碼矩陣設計

Walsh矩陣中的每個行向量是通過一組完備的正交函數系Walsh函數等間隔采樣得到的，該Walsh函數只有兩個取值,分別是+1和-1，假設對N=2v個Walsh函數進行1/N=2-v等間隔采樣，那么將會得到一個N×N的Walsh矩陣.Walsh函數正交性數學表述如下：

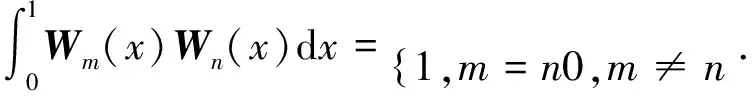
(7)

例如當v取3時，可以得到如下Walsh矩陣

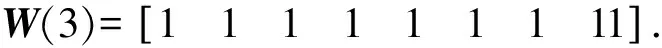
通過采樣生成的Walsh矩陣，僅包含兩個元素+1和-1，對應到相位上是0和π，滿足正交二相碼生成邏輯，即滿足如下兩個邏輯定理：

定理1 多個長度為N的二相碼序列彼此正交的必要條件是N為偶數，且取值為+1和-1的子碼數相等；

定理2 長度為2m正交二相碼序列，可以找到至少包含2m-1個序列構成的正交編碼簇，其中任意兩個編碼之間滿足嚴格正交性約束.

定理證明如下：

定理1的證明：已知二相碼編碼中每個碼元序列的取值只能是+1和-1(分別對應于信號相位0和π)，隨機取兩個彼此正交的編碼序列M1和M2，兩個二相編碼序列的長度均為N，然后逐個比較兩個編碼序列的碼元，記符號相同的碼元個數為N1，符號不同的碼元個數為N2，則有N1+N2=N.為保證兩個二相碼序列嚴格正交性，N1和N2需滿足N1=N2，所以有

N=N1+N2=2N1=2N2.

(8)

由此可見，N必須是偶數才能夠保證嚴格正交性，而且為控制編碼序列的自相關旁瓣，二相碼序列取+1和-1的數量必須相等，證明完畢.

定理2的證明：利用歸納法，當m=2時定理顯然成立，且根據定理1，任意一個二相碼序列中+1和-1的個數相等.

假定當m=k0≥2時定理2成立，即存在一個編碼長度為N=2k0，含N-1個正交二相碼的編碼簇，記編碼序列為mi，i=1,2,…,N-1.

先構造出三個長度都為2N的二相碼簇，第一個記為D，編碼總數為N-1，表示為

D={d|di=mi‖mi,i=1,2,…,N-1};

(9)

第二個記為E，編碼總數為N-1，表示為

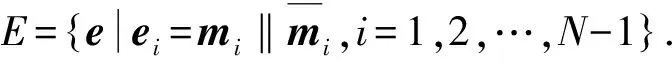
(10)

第三個記為F，它只含一個編碼序列

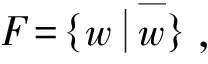
(11)

w為長度為N的全+1二相碼串，則并接在一起的為全-1的二相碼串.

從簇D和E中各取一個元素di和ej，考察兩串二相碼之間的正交性，顯然有：

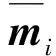
如果i=j，則兩串二相碼之間符號相同和相反的子碼數量各為N，則推出di與ej正交；于是有D與E正交.

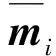
記G為F、D和E三者間的交集，綜合前面的推理可知G中所有元素取+1和-1的子碼個數相同，并且所有元素兩兩滿足正交的條件，而G中元素的個數為

2(N-1)+1=2(2k0-1)+1=2k0+1-1,

(12)

這說明m=k0+1時定理成立.綜合上述過程可知，定理2成立.

通過生成邏輯，Walsh矩陣僅僅滿足二相碼信號間的嚴格正交性，并且沒有考慮到信號的相關旁瓣輸出，需要利用遺傳算法對相關旁瓣量進行優化選擇以滿足實際需求.由于設計出的正交二相碼信號相位個數較少，因此需要拓展相位個數，以四相碼為例構造出的類Walsh矩陣形式為

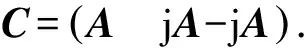
(13)

式中矩陣A為一個N×N的Walsh矩陣，通過A矩陣構造出2N×2N的矩陣C就滿足相位個數為四相的正交矩陣，證明如下：

定義ci,cj分別表示為矩陣C的第i,j行，ai,aj分別表示矩陣A的第i,j行.當i,j>N時，則ai=ai-N,aj=aj-N，并且矩陣A中任意兩個行向量具有嚴格正交性，這是由正交Walsh陣的性質決定的，那么C中行向量的取值存在如下兩種情況(i,j顯然不能取相同的值)：

第一種情況，i,j同時取在前N行或者后N行，那么

ci·cj=ai·aj±j(ai·aj)

=0±j0

=0;

(14)

第二種情況，i,j一個取前N行，一個取在后N行，那么當j=i+N時,

ci·cj

=ai·(-j)aj+jai·aj

=ai·(-j)ai+jai·ai

=-jN+jN

=0,

(15)

當j≠i+N時,

ci·cj

=ai·(-j)aj+jai·aj

=ai·(-j)aj-N+jai·aj-N

=-j0+j0

=0.

(16)

證明完畢.以此類推可以設計出滿足8相、16相等類Walsh矩陣，由于Walsh矩陣可以無限制的擴展，因此本文設計出的多相編碼信號的編碼長度可以無限擴展，但是擴展的編碼長度必須為2的正次方倍，原因從二相生成邏輯看，Walsh矩陣可以按照2的次方倍無限擴展，類Walsh矩陣大小與Walsh矩陣存大小存在2倍的關系，因此設計出的正交信號組能夠按照2的次方倍無限擴展.

但是，設計出來的類Walsh矩陣從整個生成邏輯上看僅僅是保證了信號間的嚴格正交性，對于相關旁瓣量依然沒有考慮，因此要獲得低相關旁瓣量的信號組，需要在類Walsh矩陣形成的嚴格正交性空間域上，利用遺傳算法進行優化選擇.類Walsh矩陣形成的嚴格正交性空間域是指對類Walsh矩陣進行初等列變換后可能形成的各種正交矩陣的集合，由于列變換打亂了原有相位編碼的排列順序，所以通過不同的列變換可以形成不同旁瓣量的正交信號組，根據矩陣理論相關知識了解，列變換不會影響正交矩陣行向量間的嚴格正交性.

3 遺傳算法優化選擇

通過重新編排Walsh陣生成類Walsh矩陣，如果直接從其中任意選取某幾個行向量作為雷達發射的相位編碼信號組，那么信號間具有嚴格正交性，但是相關旁瓣輸出是否比較低卻不能保證.并且由于Walsh矩陣生成邏輯的限制，直接抽取其中某幾個行向量作為雷達發射信號的編碼序列則很容易被破譯，從而增大了雷達基站被發現的概率，因此需要通過遺傳算法對類Walsh矩陣生成的嚴格正交性空間域進行優化選擇，打亂原有的編碼排列邏輯，得到低自相關峰值旁瓣量、低互相關峰值量以及低“和信號”相關峰值旁瓣量的發射信號組.以四相碼為例介紹總體設計步驟，流程框圖如圖1所示.

根據流程框圖具體設計步驟如下：

第一步，生成Walsh矩陣A，并按公式(13)編排后生成類Walsh矩陣C作為初始嚴格正交性空間域的一組值.

第二步，產生初始種群即對設置好大小種群的每個個體的染色體進行編碼，每個染色體由兩部分組成：一部分編碼將譯碼成正交四相碼陣的隨機列重排，另一部分編碼將譯碼為對隨機列重排后四相碼矩陣的隨機行抽取.例如需求編碼長度為N=4，信號個數L=2的信號組，染色體編碼形式如下：

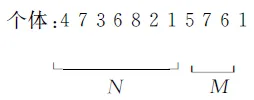
譯碼表述為：原正交四相碼矩陣的第3列、第4列、第1列和第2列重排成為新正交四相碼矩陣的第1列、第2列、第3列和第4列，抽取的信號組為新正交四相碼矩陣的第2行和第4行.

第三步，適應度值的計算與分配，適應度值的代價函數由自相關峰值旁瓣量、互相關峰值量、“和信號”相關峰值旁瓣量三部分組成，目的在于能夠使得發射信號在空間上能量分布均勻，以及提升綜合信號對目標的檢測性能.

第四步，利用遺傳算法中的遺傳算子(選擇、交叉、變異)對種群進行優化更新.

第五步，重復第三步和第四步直到滿足結束條件即遺傳代數達到設定的最大值.

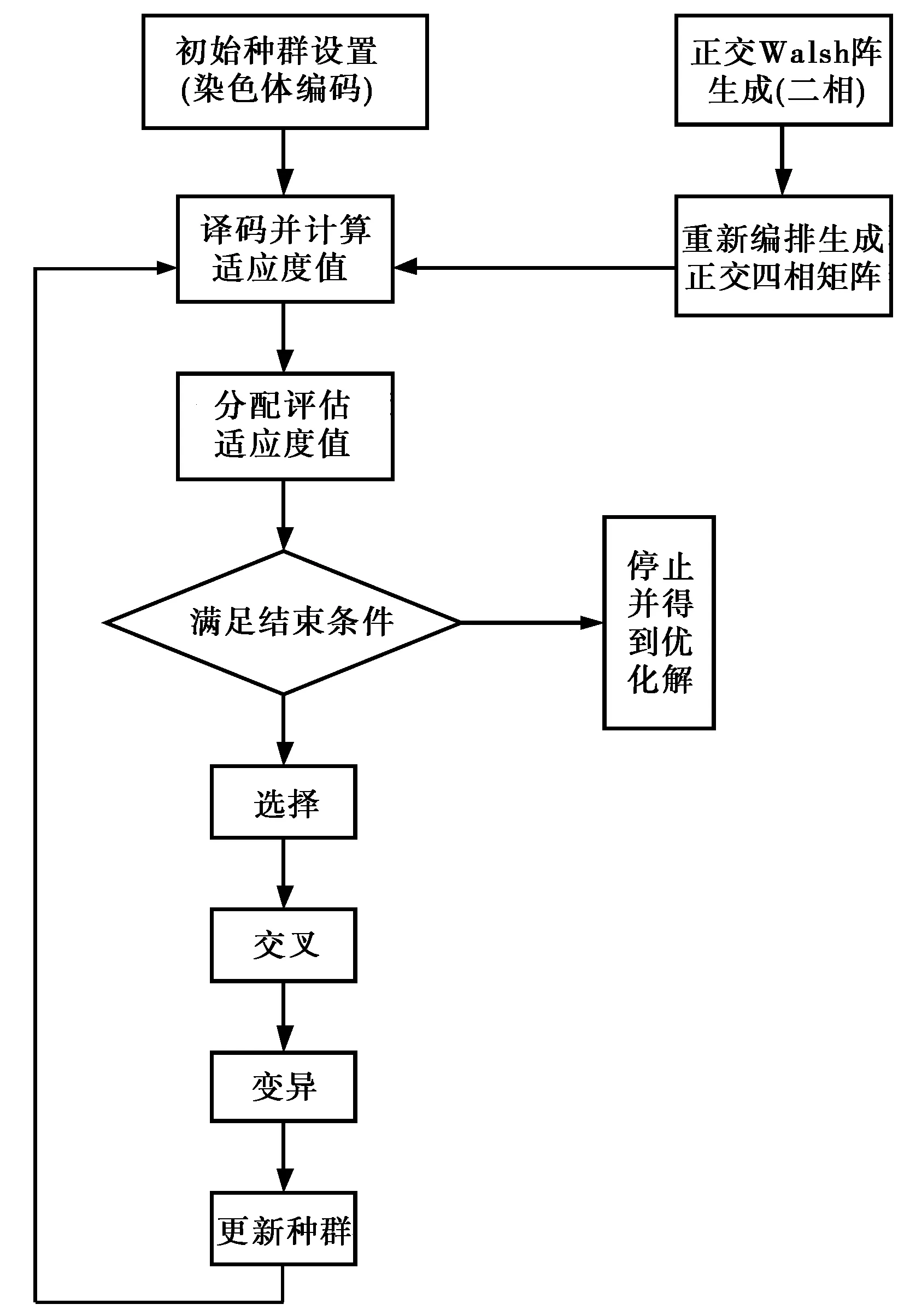
圖1 流程框圖

4 仿真結果

仿真參數設置為編碼長度N=1 024，信號個數選擇L=4，相位個數選擇為四相，最大遺傳代數為100.遺傳算法優化結束后得到的信號組的歸一化相關峰值如表1所示.

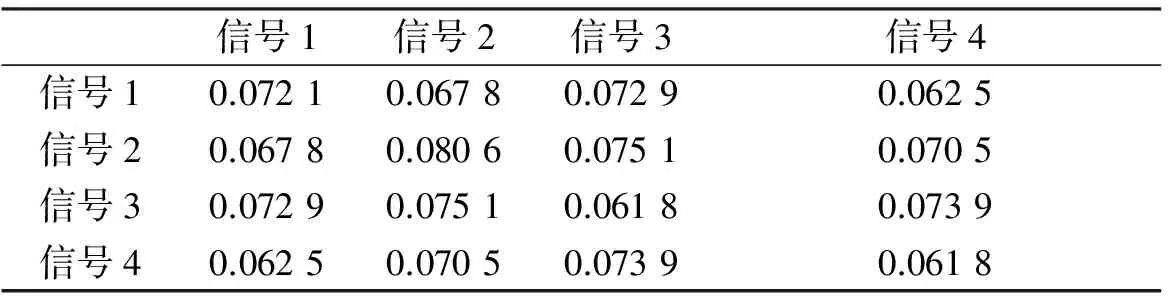
表1 優化后四相碼相關峰值表

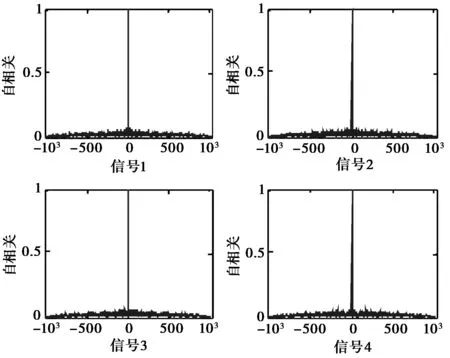
圖2 優化后四相碼自相關圖

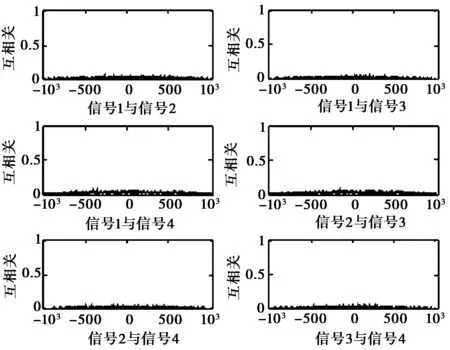
圖3 優化后四相碼互相關圖

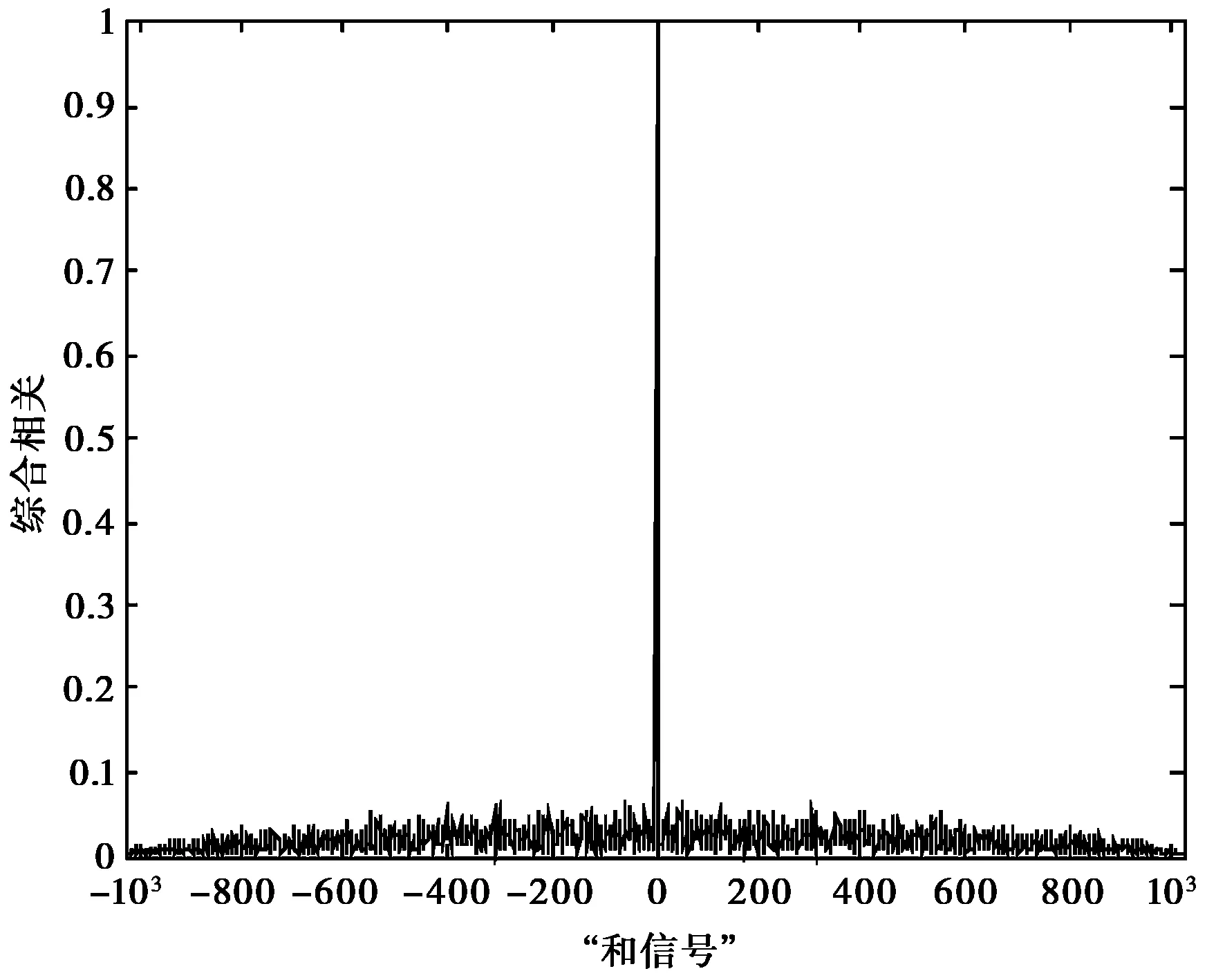
圖4 優化后四相碼“和信號”相關圖

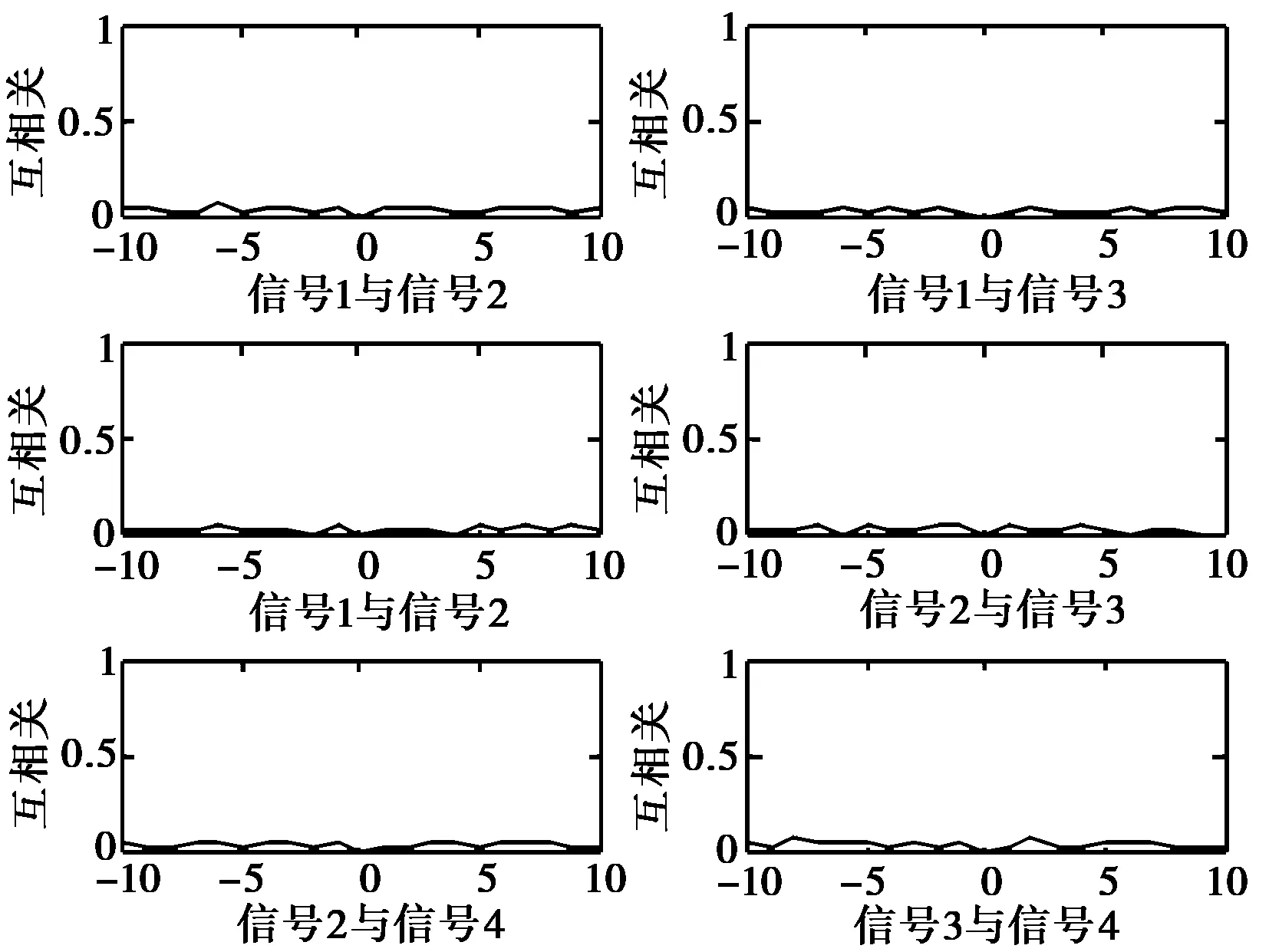
圖5 優化后四相碼互相關局部圖

根據表1得到平均自相關峰值旁瓣量(平均ASP)為0.069 1，平均互相關峰值量(平均CP)為0.070 5即-23.160 3 dB和-23.031 0 dB，“和信號”相關峰值旁瓣為0.061 5(-24.082 4 dB)，所有相關旁瓣量比較低.

設計出的四相碼信號的歸一化自相關整體圖如圖2所示；歸一化互相關整體圖如圖3所示；歸一化“和信號”相關輸出如圖4所示.

由圖2～4可見“和信號”相關輸出旁瓣電平、自相關旁瓣電平和互相關旁瓣電平都是比較低的，使得信號組的抗截獲性能更高，同時更容易檢測到弱目標并使虛假目標的出現概率降低.

本文的又一個關鍵點在于設計出的信號組滿足嚴格正交性，通過圖5(互相關局部放大圖)可以看出信號間在目標零點偏移處互相關量輸出為0，說明該方法是可行的.嚴格正交性的滿足，使得信號在角度測量精度和雜波對消效果上得到了很大的提升.

下面針對設計出的正交多相編碼信號做多普勒容忍性能分析，設置脈沖重復周期為tr，占空比為η=20%，那么一個脈沖周期內信號持續時間tp=0.2tr.多普勒頻率為fd，歸一化后的多普勒分辨率(歸一化多普勒為fd*tr=fd*5tp)如圖6所示.

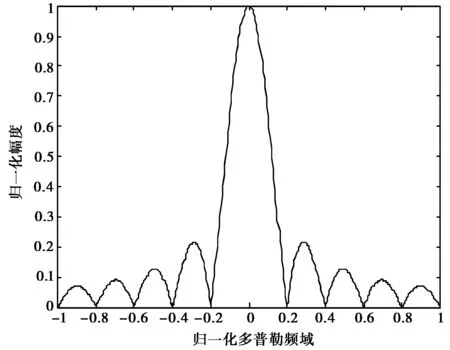
圖6 歸一化多普勒分辨率

通過圖6發現該信號組多普勒分辨率僅與脈沖持續時間有關，與相位編碼序列的排列順序無關，具有一般相位編碼信號多普勒容忍性較差的特性，因此相位編碼信號一般用于檢測靜止目標，如果用于探測運動目標，則需要在信號處理端進行多普勒預補償.

5 結 論

正交相位編碼是正交信號的一種重要形式，被廣泛的應用于MIMO雷達上.多相碼的設計使得雷達信號隱蔽性更強，實際雷達發射相位編碼信號需求低綜合旁瓣量，從而便于對目標的檢測.本文提出了一種正交多相碼的設計方法.Walsh函數正交性能的利用使得設計出的多相碼序列具有嚴格正交性，便于提升角度測量精度和雜波對消效果；遺傳算法在正交性空間域上優化選擇使得信號組具有低旁瓣量，降低了傳統遺傳算法的優化運算量；增加“和信號”形式的代價函數，使得遺傳算法優化出的信號組提升了目標檢測性能.

但是，本文設計出來的信號組仍然是相位編碼信號，它具有相位編碼信號的特有屬性，例如對多普勒比較敏感等，這就需要在接收信號處理時，進行多普勒預補償來解決該問題.

[1] 何子述,韓春林,劉 波.MIMO雷達概念及其技術特點分析[J].電子學報,2005,33(12A):2441-2445.

HE Zishu,HAN Chunlin,LI Bo.MIMO radar and its technical characteristic analysis[J].Chinese Journal of Electronics,2005,33(12A):2441-2445.(in Chinese)

[2] 王 勇,廖桂生,王喜媛.MIMO系統空時特征波束性能分析[J].電波科學學報,2009,24(2):297-301.

WANG Yong,LIAO Guisheng,WANG Xiyuan.Performance analysis of space-time eigen-beamforming in MIMO systems[J].Chinese Journal of Radio Science,2009,4(2):297-301.(in Chinese)

[3] 劉韻佛,劉 崢,謝 榮.一種基于擬牛頓法的MIMO雷達發射方向圖綜合方法[J].電波科學學報,2008,23(6):1188-1192.

LIU Yunfo,LIU Zheng,XIE Rong.Transmit pattern synthesis algorithm for MIMO radar based on Newton-like method[J].Chinese Journal of Radio Science,2008,23(6):1188-1192.(in Chinese)

[4] 楊 進,邱兆坤,黎 湘,等.一種基于混沌序列的隨機離散頻率編碼信號[J].電子與信息學報,2011,V33(11):2702-2708

YANG Jin,QIU Zhaokun,LI Xiang,et al.Random discrete frequency coding signal based on chaotic series[J].Journal of Electronics & Information Technology,2011,V33(11):2702-2708.(in Chinese)

[5] 劉 波,韓春林,苗江宏.MIMO雷達正交LFM信號設計及性能分析[J].電子科技大學學報,2009,38(1):28-31.

LIU Bo,HAN Chunlin,MIAO Jianghong.OFD-LFM signal design and performance analysis for MIMO radar[J].Journal of University of Electronic Science and Technology of China,2009,38(1):28-31.(in Chinese)

[6] DENG H.Polyphase code design for orthogonal netted radar systems[J].IEEE Trans on Signal Processing,2004,52(11):3126-3135.

[7] LIU Bo,HE Zishu,ZENG Jiankui,et al.Polyphase orthogonal code design for MIMO radar systems[C]// International Conference on Radar.Shanghai,October 16-19,2006,1:113-116.

[8] DENG H.Synthesis of binary sequences with good autocorrelation and cross-correlation properties by simulated annealing[J].IEEE Trans Aerosp Electron Syst,1996,32(1):98-107.

[9] LI J,STOICA P,XU L Z,et al.On parameter identifiability of MIMO radar[J].IEEE Signal Processing Letters,2007,14(12):968-971.

[10] 劉紅明,何子述,李 軍.雙基地MIMO雷達發射陣目標角度估計[J].電波科學學報,2010,25(3):499-504.LIU Hongming,HE Zishu,LI Jun.Transmitter array target angle estimates for bistatic MIMO radar[J].Chinese Journal of Radio Science,2010,25(3):499-504.(in Chinese)

[11] SUN Ying,HE Zishu,LIU Hongming,et al.Binary orthogonal code design for MIMO radar systems[C]// IEEE 2010 international symposium on intelligent signal processing and communication systems.Chengdu,December 6-8,2010.