基于短波測量數(shù)據(jù)的信道模型聚類方法

金 珠 吳永宏 任源博 管英祥 蔣宏奎

(中國電波傳播研究所，山東 青島 266107)

引 言

對于依靠電離層反射的短波信道而言，電離層的分層結(jié)構(gòu)、電離層多模式傳播和多跳傳播、電離層不均勻性和不規(guī)則運動，以及電離層的吸收、反射損耗共同決定了短波信道的傳播特性，使得短波信道的多徑延時、衰落、多普勒頻移和多普勒展寬在產(chǎn)生機(jī)理和表現(xiàn)方式上區(qū)別于蜂窩信道[1-2]．信道測量是研究短波信道傳播特性的有效途徑，通過對信道測量數(shù)據(jù)分析，可以得出某次傳播數(shù)據(jù)的信道參數(shù)，但是這些參數(shù)表現(xiàn)為隨機(jī)、離散特性，無法用來描述某個鏈路的信道特性．論文提出了使用減法聚類算法[3]，按照一定刻度將某鏈路實測數(shù)據(jù)提取出的信道參數(shù)分別進(jìn)行一維和多維聚合分類，從而得到表征此鏈路特性的典型信道參數(shù)和信道模型．

1 信道測量數(shù)據(jù)分析

1.1 數(shù)據(jù)說明

論文使用的信道測量數(shù)據(jù)是2012年1月12日至2012年1月17日由青島發(fā)射，北京接收的數(shù)據(jù)，發(fā)射數(shù)據(jù)是由一串PN信號組成，每次突發(fā)波形的時長為30 s，產(chǎn)生數(shù)據(jù)樣本為1 482個，其中有效數(shù)據(jù)(接收信噪比>-3 dB)1 135個．

1.2 數(shù)據(jù)分析原理

數(shù)據(jù)分析的原理是基于PN序列特性，使用相關(guān)法求得信道沖擊響應(yīng)函數(shù)，再由信道沖激響應(yīng)求得信道散射函數(shù)，從而得到一系列信道參數(shù)[4-5]．設(shè)發(fā)送原始信號為

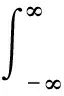
(1)

式中:c(τ,t)表示信道沖激響應(yīng);n(t)表示噪聲．當(dāng)輸入信號x(t)是由時間長度為T的PN序列組成的信號時，經(jīng)過單位沖激響應(yīng)為c(τ,t)的信道后，將接收到的信號y(t)以時間長度T分段，取第l段信號yl(t)與輸入信號x(t)做相關(guān)運算

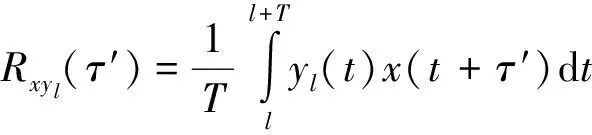
(2)

由公式(2)，可以得到?jīng)_激響應(yīng)函數(shù)在τ=τ′,t=tl時的值，當(dāng)變化τ′和tl時，就可以得到?jīng)_激響應(yīng)函數(shù)C(τ,t)．信道C(τ,t)的時變特性可以看作以t為變量的平穩(wěn)隨機(jī)過程，C(τ,t)的自相關(guān)函數(shù)[6]

RC(τ1,τ2,Δt)=E[C(τ1,t)C*(τ2,t+Δt)],

(3)

在多徑信道中，衰落與延時認(rèn)為不相關(guān)，可得

RC(τ1,τ2,Δt)=RC(τ1，Δt)δ(τ1-τ2)，

(4)

式(4)可表示為RC(τ,Δt)=E[C(τ,t)C*(τ,t+Δt)],

(5)

以Δt為變量通過對式(5)做傅里葉變換可得

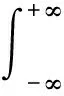
(6)

s(τ,υ)為散射函數(shù)．

1.3 信道參數(shù)計算

文中希望通過對信道測量數(shù)據(jù)的分析，得到由電離層反射信道引起的、對短波通信影響很大的時頻色散參數(shù)，并使用這些參數(shù)歸納短波信道模型．

1) 最大附加延時

描述時間色散的參數(shù)有平均附加延時、延時展寬和最大附加延時，這些參數(shù)都可以由延時功率譜得到[7]，延時功率譜(如圖1所示)可以通過1.2節(jié)的散射函數(shù)得到

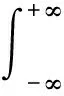
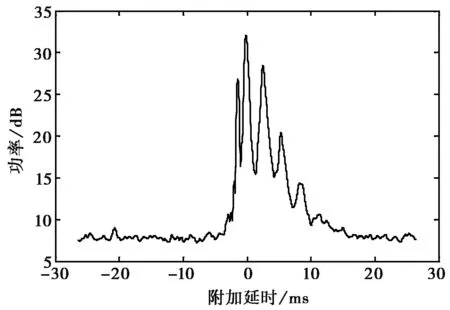
圖1 延時功率譜

(7)

由于信道參數(shù)統(tǒng)計聚類出的信道模型應(yīng)貼近短波調(diào)制解調(diào)器的設(shè)計，因此選擇計算最大附加延時．延時功率譜是基于固定延時參考量τ0的附加延時τ的函數(shù)，τ0是第一個到達(dá)的可檢測信號．計算最大附加延時dτ時，選取延時功率譜多徑分量的最大值max(P(τ))為參照，設(shè)置一個噪聲門限值max(P(τ))-X為噪底，以區(qū)分接收的多徑分量和加性噪聲，其中X的取值范圍為6～10 dB．那么最大附加延時

dτ= max(τ|(P(τ)-max(P(τ)))>-X) -min(τ|(P(τ)-max(P(τ)))>-X),

(8)

2) 多普勒展寬

信道的頻域色散特性可用多普勒展寬參數(shù)來描述，由散射函數(shù)可得到多普勒功率譜

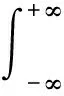
(9)

數(shù)據(jù)多普勒功率譜如圖2所示，多普勒展寬即多普勒功率譜二階中心矩的平方根[7]． 那么多普勒展寬為

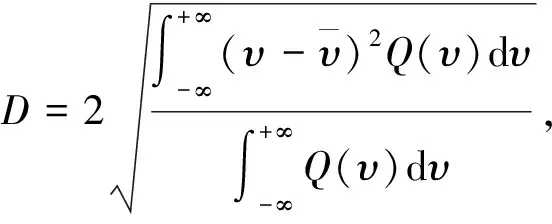
(10)

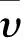
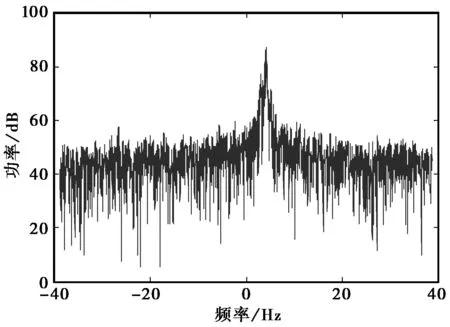
圖2 多普勒功率譜

2 信道模型聚類

2.1 聚類算法原理

聚類是將一個數(shù)據(jù)集劃分為若干組，使組內(nèi)相似性大于組間相似性，實現(xiàn)這樣一種劃分需要一個相似度度量，即取兩個輸入向量，返回反映這兩個向量間相似性的數(shù)值．由于大多數(shù)相似度度量對輸入向量中心元素值域非常敏感，因此每個輸入度量都必須歸一化，即其絕對值在單位區(qū)間[0,1]內(nèi)．

減法聚類的原理[5]是將每個數(shù)據(jù)點作為可能的聚類中心，并根據(jù)各個數(shù)據(jù)點周圍的數(shù)據(jù)點密度來計算該點作為聚類中心的可能性．在迭代出第一個聚類中心后，從剩余的可能作為聚類中心的數(shù)據(jù)點中，繼續(xù)采用類似的方法選擇下一個聚類中心，這一過程一直持續(xù)到所有剩余數(shù)據(jù)點作為聚類中心的可能性低于某一閾值時，從而決定輸入和輸出變量的隸屬度函數(shù)個數(shù)．

設(shè){x1,x2,…,xi,…，xn}是s維空間的n個數(shù)據(jù)點，不失一般性，假定數(shù)據(jù)點都已歸一化到一個超立方體中，將每個數(shù)據(jù)點都作為聚類中心的侯選點．計算每個數(shù)據(jù)點xi的密度指標(biāo)

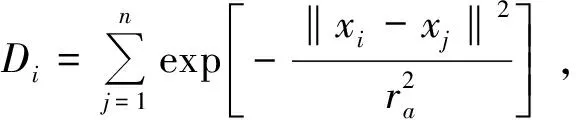
(11)

式中ra是一個正數(shù)，定義了該點的鄰域直徑，如果數(shù)據(jù)點xi周圍有多個鄰近的數(shù)據(jù)點，則xi具有高密度值，半徑以外的數(shù)據(jù)點對該點的密度指標(biāo)貢獻(xiàn)非常小．計算每個數(shù)據(jù)點的密度指標(biāo)后，選取具有最高密度指標(biāo)的數(shù)據(jù)點xc1作為第一個聚類中心，Dc1為密度指標(biāo)．設(shè)當(dāng)前選出了第k個聚類中心xck，其密度指標(biāo)為Dck，則用Dck修正每個數(shù)據(jù)點的密度指標(biāo)

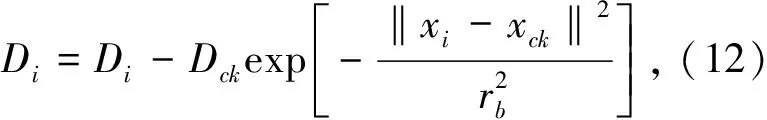
式中rb是一個正數(shù)，定義了一個密度指標(biāo)函數(shù)顯著減小的鄰域，通常rb>ra，以避免出現(xiàn)相距很近的聚類中心，這里取rb=1.5ra．通過修正后，顯然靠近聚類中心的數(shù)據(jù)點的密度指標(biāo)將顯著減小，使得這些點不太可能被選為下一個聚類中心．按下面算法來對第k個聚類中心進(jìn)行判決：

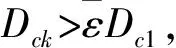
2) 當(dāng)Dck<εDc1，認(rèn)為xck不是聚類中心，終止聚類過程．

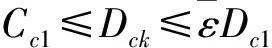
(13)

式中dmin為xck已經(jīng)確定的聚類中心距離的最小值，當(dāng)式(13)成立時，認(rèn)為xck是聚類中心，當(dāng)式(13)不成立時，認(rèn)為xck不是聚類中心，并將該數(shù)據(jù)點的密度指標(biāo)設(shè)為0，選擇余下數(shù)據(jù)點中具有最高密度指標(biāo)的點為待確認(rèn)的點，重新進(jìn)行判決．

2.2 聚類結(jié)果

使用2.1節(jié)介紹的聚類算法對青島北京鏈路的最大附加延時和多普勒展寬參數(shù)做一維和二維聚類統(tǒng)計，可得到對應(yīng)參數(shù)的典型值及此鏈路的典型信道模型．

1) 一維參數(shù)聚類結(jié)果

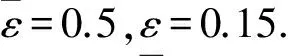
表1 一維參數(shù)聚類結(jié)果

2) 二維參數(shù)聚類結(jié)果

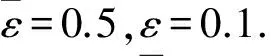
表2 二維參數(shù)聚類結(jié)果

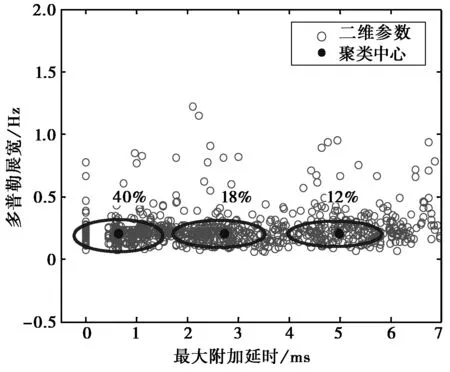
圖5 最大附加延時和多普勒展寬二維參數(shù)的分布特性

由以上的聚類結(jié)果可以看出，文中所用的測量鏈路和測量時間段內(nèi)，信道的路徑延時差異較大，而小尺度衰落，即多普勒展寬差異較小．

2.3 聚類結(jié)果驗證

使用聚類算法的目標(biāo)是聚類出的典型信道參數(shù)及信道模型出現(xiàn)概率大并且參數(shù)集中度高，因此可以通過計算聚類中心半徑范圍內(nèi)參數(shù)所占比例來驗證聚類結(jié)果的合理性．

從圖3(見 571 頁)可以看出，最大附加延時落在聚類中心1半徑范圍內(nèi)的值占所有參數(shù)比例接近40%，落在聚類中心2和3的值分別占比例為20%和18%，依次劃分的典型信道參數(shù)類型包含了78%的信道參數(shù)值．并且，使用聚類算法找出的信道參數(shù)典型值具有發(fā)生概率大和代表不同信道特性的特點．同樣，從圖4(見 571 頁)可看出多普勒展寬值的聚類結(jié)果滿足要求．從圖5可以看出，二維參數(shù)落在聚類中心1、2和3的半徑范圍內(nèi)的概率分別為40%、18%和12%，依次劃分的信道模型包含了70%的二維信道參數(shù)種類．聚類中心均落在參數(shù)發(fā)生概率大、集中度高的位置，并且三個聚類中心可以代表三種不同的信道模型．

2.4 分時段聚類結(jié)果及信道質(zhì)量評價

短波信道特性隨季節(jié)、時段、太陽黑子等變化而變化，因此通過將具有同樣季節(jié)、時段、太陽黑子參數(shù)的數(shù)據(jù)用來做聚類分析更具有科學(xué)性．由于論文使用測量數(shù)據(jù)存在局限性(僅限于前后6天的測量數(shù)據(jù)，且樣本數(shù)量較少)，根據(jù)短波信道特性，可將測量數(shù)據(jù)分為白天(5∶00—21∶00時)和晚上(22∶00—23∶00時，及1∶00—4∶00時)兩個時段，按照上述聚類方法聚類，可分別得到白天時段和晚上時段的最大附加延時和多普勒展寬二維參數(shù)的聚類結(jié)果，如表3、表4所示，其中聚類中心1對應(yīng)的信道模型發(fā)生概率大于聚類中心2，聚類中心2對應(yīng)的信道模型發(fā)生概率大于聚類中心3．由聚類結(jié)果可看出，白天時段信道的路徑延時小于晚上時段，而多普勒展寬無明顯差異．

表3 白天時段二維參數(shù)聚類結(jié)果

表4 晚上時段二維參數(shù)聚類結(jié)果

以小時為單位，分別計算出白天時段和晚上時段對應(yīng)測量數(shù)據(jù)的二維信道參數(shù)落在表3和表4中每個聚類中心半徑范圍內(nèi)的概率，分別如圖6、圖7所示，橫坐標(biāo)代表時刻(以小時為單位計)，縱坐標(biāo)代表在對應(yīng)時刻內(nèi)，信道參數(shù)落在每種聚類中心半徑范圍內(nèi)的概率，當(dāng)數(shù)據(jù)樣本足夠多時，可以認(rèn)為在對應(yīng)時刻內(nèi)，每個聚類中心對應(yīng)的信道模型發(fā)生概率．從圖6可以看出，在白天時段，8時至15時的時段內(nèi)，聚類中心1和聚類中心2的發(fā)生概率較大，信道情況較好，而與此時段相聚越遠(yuǎn)的時段，聚類中心3的概率越大，信道情況越差．從圖7可以看出，聚類中心1對應(yīng)的最差信道在凌晨1時發(fā)生的概率最大，而與1時相距越遠(yuǎn)的時刻，聚類中心1的發(fā)生概率越小，聚類中心2的發(fā)生概率越大，信道特性越好．因此根據(jù)聚類中心對應(yīng)的信道模型在不同時刻的分布情況，可以定量描述信道特性．

綜上所述，使用聚類法分析信道模型，既可以得到不同信道模型的典型參數(shù)(聚類中心)，又可以將信道特性按照一定刻度分類，來定量描述和評價信道質(zhì)量．

3 結(jié) 論

依據(jù)青島-北京鏈路短波信道測量數(shù)據(jù)，從數(shù)據(jù)樣本中計算出影響短波通信的重要信道參數(shù)，使用減法聚類算法，將隨機(jī)離散的信道參數(shù)進(jìn)行歸納統(tǒng)計，得到此鏈路的典型信道參數(shù)和信道模型．通過分析一維和多維信道參數(shù)在聚類中心半徑范圍內(nèi)的分布特性驗證了聚類算法的合理性．從而解決了離散隨機(jī)信道的定量描述問題，為短波頻譜管理[8]提供了隨機(jī)信道質(zhì)量評定依據(jù)．

[1] THEODORE S. Rappaport Ts Wireless Communications Principles and Practices [M]. 4th ed. New Jersey: Prentice Hall, 2002.

[2] 姚永剛, 趙正予, 謝樹果, 等. 電離層后向散射探測中m序列和FH序列的應(yīng)用. 電波科學(xué)學(xué)報, 2001, 16(4): 522-528.

YAO Yonggang, ZHAO Zhengyu, XIE Shuguo, et al. The applications of m sequence and FH sequence to ionospheric backscattering sounding. Chinese Journal of Radio Science, 2001, 16(4): 522-528. (in Chinese)

[3] BEZDEK J C. A convergence theorem for the fuzzy ISODATA chustering algorithms [J]. Transaction on Pattern Analysis and Machine Intelligence, 1982, 2(1):1-8.

[4] CHEN C C, HUANG C C. Fast feedforward channel sounding RAKE receiver[J]. Electronics Lerrers, 2000, 36(20):1731-1733.

[5] WATTERSON C C, JUROSHEK J R, BENSEMA W D. Experimental confirmation of an HF channel model[J]. Transaction on Communication Technology, 1970, 18(6):792-803.

[6] 涂旭東. 寬帶短波信道特性和建模研究[D]. 四川成都: 電子科技大學(xué), 2004.

TU Xudong. Wideband HF Channel Characteristics and Modeling Study[D].Chengdu Sichuan: University of Electronic Science & Technology of China, 2004.(in Chinese)

[7] BALABAN J R, SHANMUGAN S K. Simulation of Communication Systems: Modeling: Methodology and Techques[M]. 2nd ed. New Yonk:kluwer Academic Publishers, 2000.

[8] CAPAR F, JONDRAL F. Resource allocation in a spectrum pooling system for packet radio networks using OFDM/TDMA[C]∥ IST Mobile and Wireless Telecommunications Summit, Thessaloniki,2002.