一種實驗室合成孔徑雷達對目標散射的成像試驗

葛亦斌 金亞秋 王海鵬

(復旦大學波散射與遙感信息重點實驗室，上海200433)

引 言

雷達系統發射線性調頻連續波(Frequency Modulated Continuous Wave,FMCW)，通過雷達平臺的移動使雷達天線按照一定的虛擬單元構成天線單元，合成等效大孔徑天線，提高了方位向分辨率[1-3].該合成孔徑雷達(Synthetic Aperture Radar,SAR)對目標高分辨率檢測成像是當今遙感與目標識別的主要技術.相比脈沖波雷達[4]，FMCW雷達系統具有重量輕、成本低、功耗低、分辨率高等特點.較低的峰值功率使其隱蔽性高，對抗反輻射武器能力強[5-7].目前，FMCW雷達成像研究大多數是簡單目標的二維成像仿真[8-9]，或隱藏目標的位置探測.

本實驗室微波暗室構建了平臺移動的極化雷達成像系統，用于極化SAR對目標模型的實驗室試驗研究.采用分數階Fourier變換(Fractional Fourier Transform,FRFT)和調頻信號算法(Chirp Scaling,CSA )[10]，用FRFT提高方位向分辨率，由此提出了基于FRFT的適用于小距離徙動、近距離的目標成像算法.本實驗用一縮小尺寸的金屬坦克模型，以及用樹葉簇遮蔽下的該坦克模型進行了雷達不同入射角觀測下HH、VV、VH、HV極化回波的數據采集與極化成像.同時，采用三面體角反射器進行雷達散射截面(Radar Cross Section,RCS)定標[11]，對實驗結果與數值模擬結果進行比較與驗證.

1 全極化SAR實驗室系統

本實驗室極化雷達成像系統設計原理如圖1所示.雷達系統實驗描述見圖2，其中天線視角可變動，上下可移動，雷達沿軌道水平勻速運動.

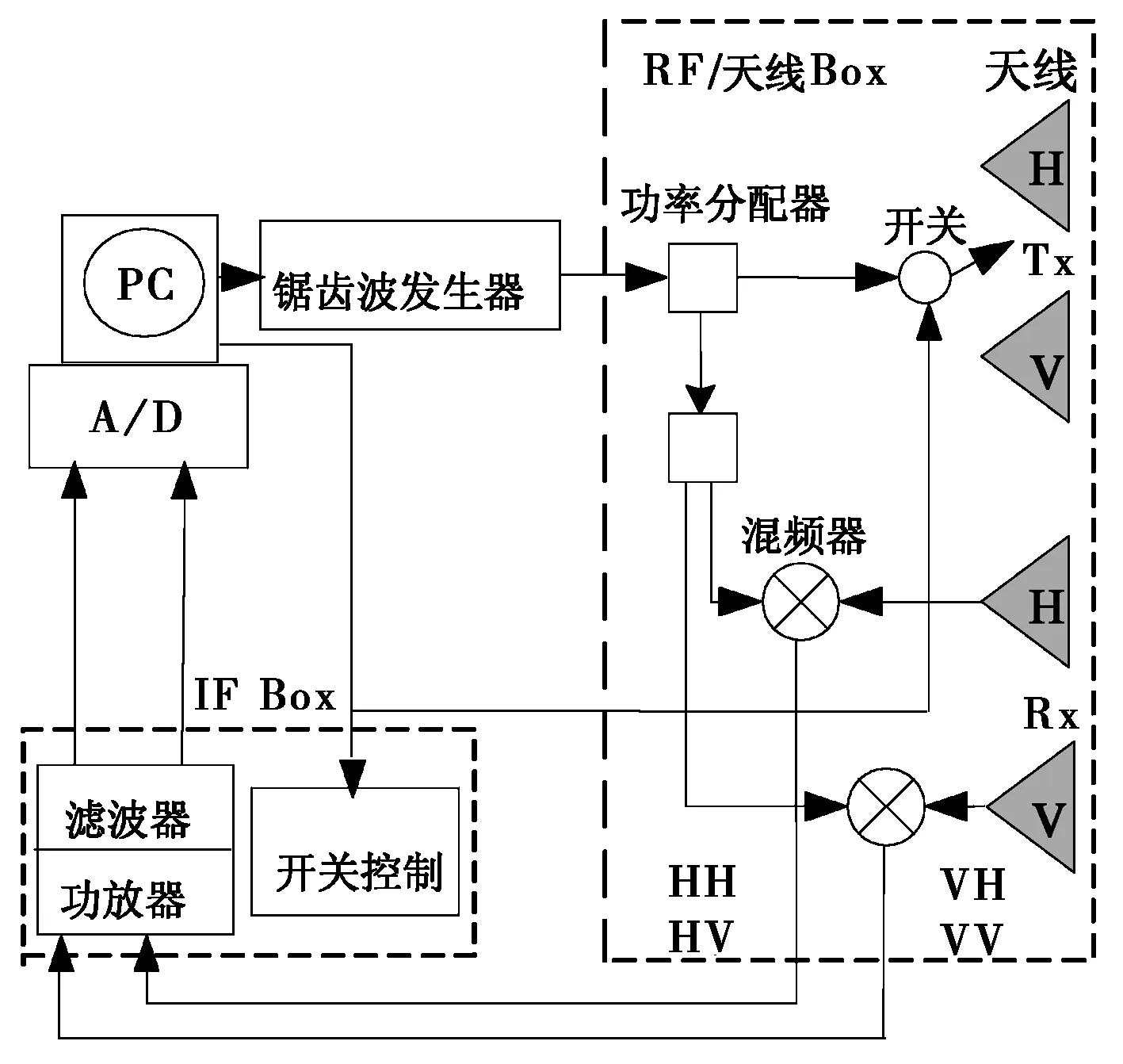
圖1 本實驗室SAR系統原理圖

圖2 本實驗室極化SAR對目標模型的實驗

雷達成像系統發射頻率為8～10 GHz調頻連續波，功率分配器產生功率相同的兩路信號，一路由開關控制交替發射水平極化波(H)和垂直極化波(V)，另一路作為參考信號和接收信號進行混頻處理.該雷達系統可以分別獲得水平與垂直同極化HH與VV，以及交叉極化VH與HV后向散射數據，構建2×2維復散射矩陣[6].

1.1 FRFT

雷達發射線性調頻信號，通過估算雷達回波方位向數據的調頻斜率，構造匹配濾波器進行方位向壓縮，進行SAR散射成像.FRFT作為一種廣義的Fourier變換，將信號在一組正交調頻信號基上展開，一個調頻信號在某一階次下的FRFT是一個沖擊函數.實驗中接收到的信號在方位向正是一個線性調頻信號，在某一特定階次下，將信號壓縮成沖擊函數，相比脈沖壓縮，主瓣壓縮和旁瓣抑制效果非常明顯[10].

信號s(t)的p階FRFT定義為

(1)

式中：FRFT變換函數為

(2)

p為FRFT的階數，參數α=pπ/2為正實數，取pπ/2=2π得周期為4.將式(2)代入式(1)有

(3)

1.2 成像算法

按圖1 FMCW成像原理，將接收信號和發射信號進行差頻處理，得到點目標函數[5]：

(4)

式中：A是振幅；f0為中心頻率；t為時間；M=B/T為調頻率，B為帶寬，T為持續時間；τ為時間延時；g=g(x0,y0,z0)是位于(x0,y0,z0)目標元的反射系數.

成像算法[10,15]如圖3描述，對接收到的信號在距離向進行快速傅里葉變換(Fast Fourter Transform, FFT)和方位向做特定階次的FRFT，分別實現距離向和方位向的壓縮，得到SAR圖像.FFT是FRFT在階次為1時的特殊情況.目標回波信號通過差頻處理，如圖4所示.差頻的結果使得回波頻率與時間延時相關，因此在距離向進行FFT，可以完成距離向壓縮.雷達平臺勻速運行，信號在方位向為線性調頻信號，而一個調頻信號在某一階次下的FRFT是一沖擊函數，在方位向進行FRFT，可以完成方位向壓縮.

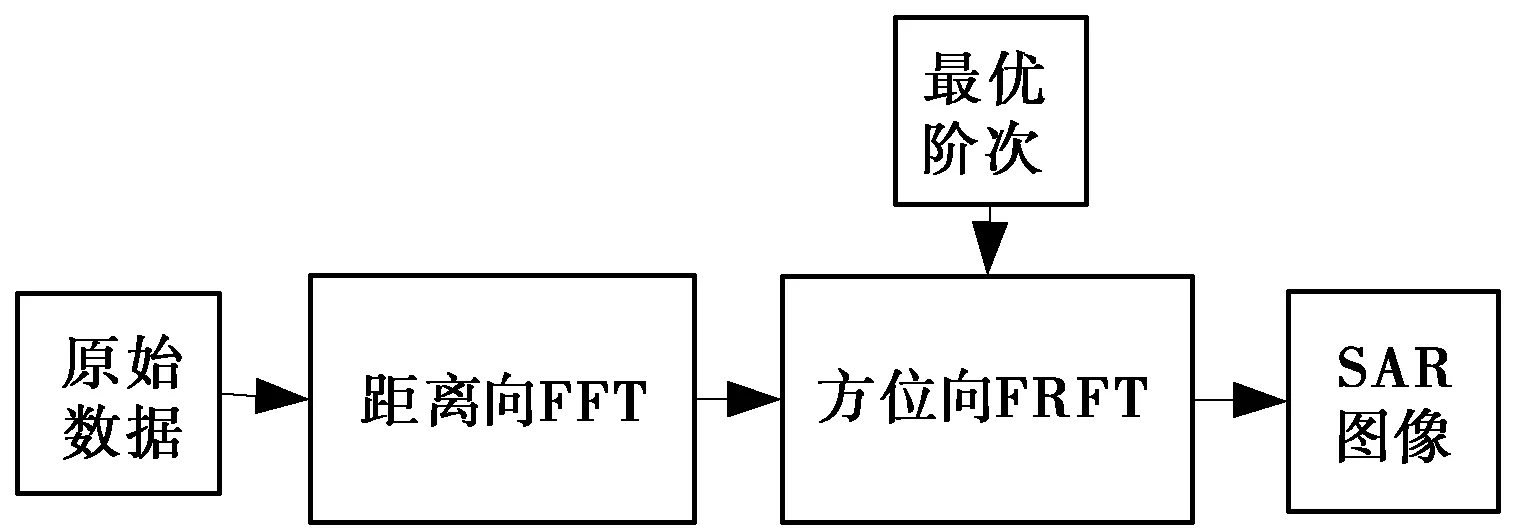
圖3 基于FRFT成像算法

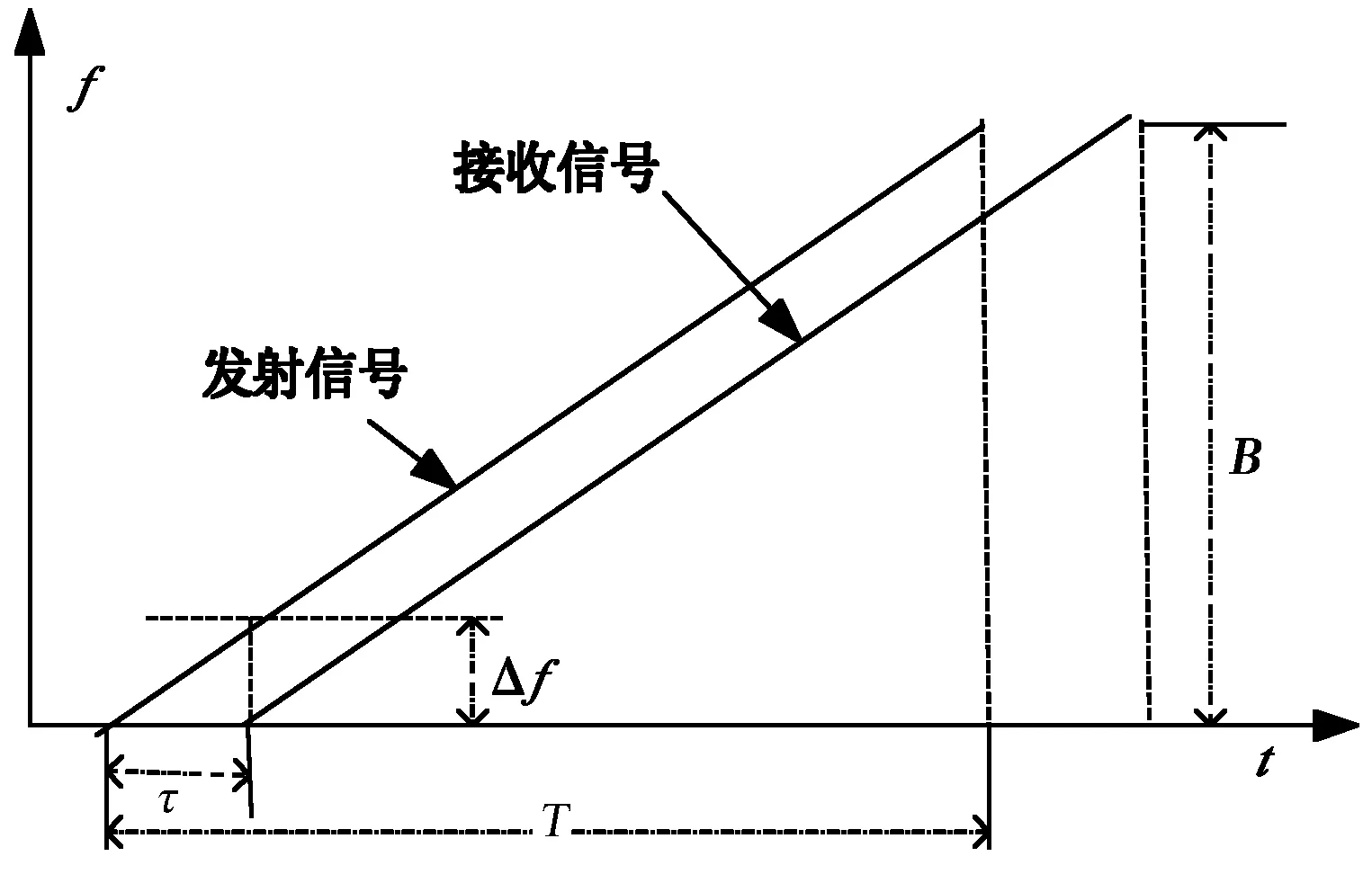
圖4 線性調頻信號頻率變換

在距離向經過對時間t的FFT變換后的表達式為

U(x,y,z)=Af(z-z0)g(x0,y0,z0)

h(x-x0,y-y0,z0).

(5)

式中：

(6)

(7)

c表示光速.當雷達沿一維x方向勻速運動時，則x-x0=νtm，y=y0，tm表示方位向時間，式(7)變為

(8)

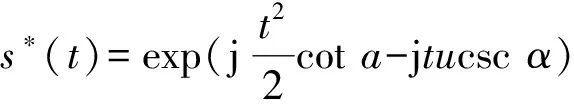
對于一個復雜體目標，回波信號在距離向經過對時間t的FFT變換后，式(5)寫為

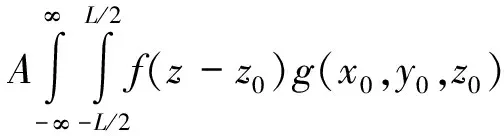
h(x-x0,y-y0,z0)dx0dy0.

(9)

式中：L表示雷達沿一維x方向運行的長度； 在y方向為無限區域積分.當目標位于z=z0，式(9)變為

h(x-x0,y-y0,z0)dx0dy0.

(10)

對式(10)兩邊進行方位向的FRFT，由于式(8)為s′(t)=exp(jat2+bt)的線性調頻信號，根據FRFT在某一階次下h(x-x0,y-y0,z0)與共扼復數卷積時可以轉換為沖擊函數δ(x-x0,y-y0,z0)，得到目標的散射數據[9]

(x0-x,y0-y,z0)dxdy.

(11)

成像分辨率由雷達工作帶寬、合成孔徑大小來決定.距離上分辨率為ΔR=c/(2B)，B為頻率偏移量.方位向分辨率為L/2，L表示雷達天線尺寸.由于雷達成像是在二維頻域上得到的，且在壓縮過程中不同維數上壓縮的比例不同，因此需要對時域和頻域的轉換，才能還原目標真實的大小.

由圖4可得，在距離向Δf/τ=B/T，τ=2R/c，因此Δf/R=2B/(cT)，頻率差Δf與雷達和目標的距離R成正比.其中τ為信號的時間延遲，Δf為發射信號與接收信號的頻率差，R為天線至目標的距離，帶寬B=2 GHz，運行持續時間T≈10 ms，因此Δf≈(4/3)×103R.

在方位向， FRFT的時移性質為

-j2πut0sinα)Fp[s(t)](u

-t0cosα).

(12)

其中p=2α/π，可以得到時間t和頻率u的對應關系：u=tcosα.

1.3 三面角體反射器RCS定標

三面體角反射器圖5是SAR定標中使用最為廣泛的無源點目標，它結構簡單、有穩定的大散射截面積RCS，且在較寬的角度范圍內RCS變化較小.其誤差大致來自于加工制作、安裝位置與偏向等.準確的三面體角反射器的加工與布設，可以減小誤差.

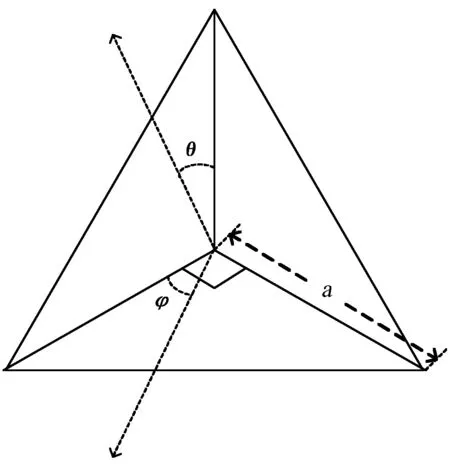
圖5 三面體角反射器模型

RCS定標流程如圖6所示.先在地面定標場中設置已知散射截面積σ的標準角反射器，雷達先對該定標目標成像，比較測得的散射值gi與標準角反射器的理論散射截面積σ，這里下標i是第i次測量.為提高比較精度，測試樣本次數應盡可能多.

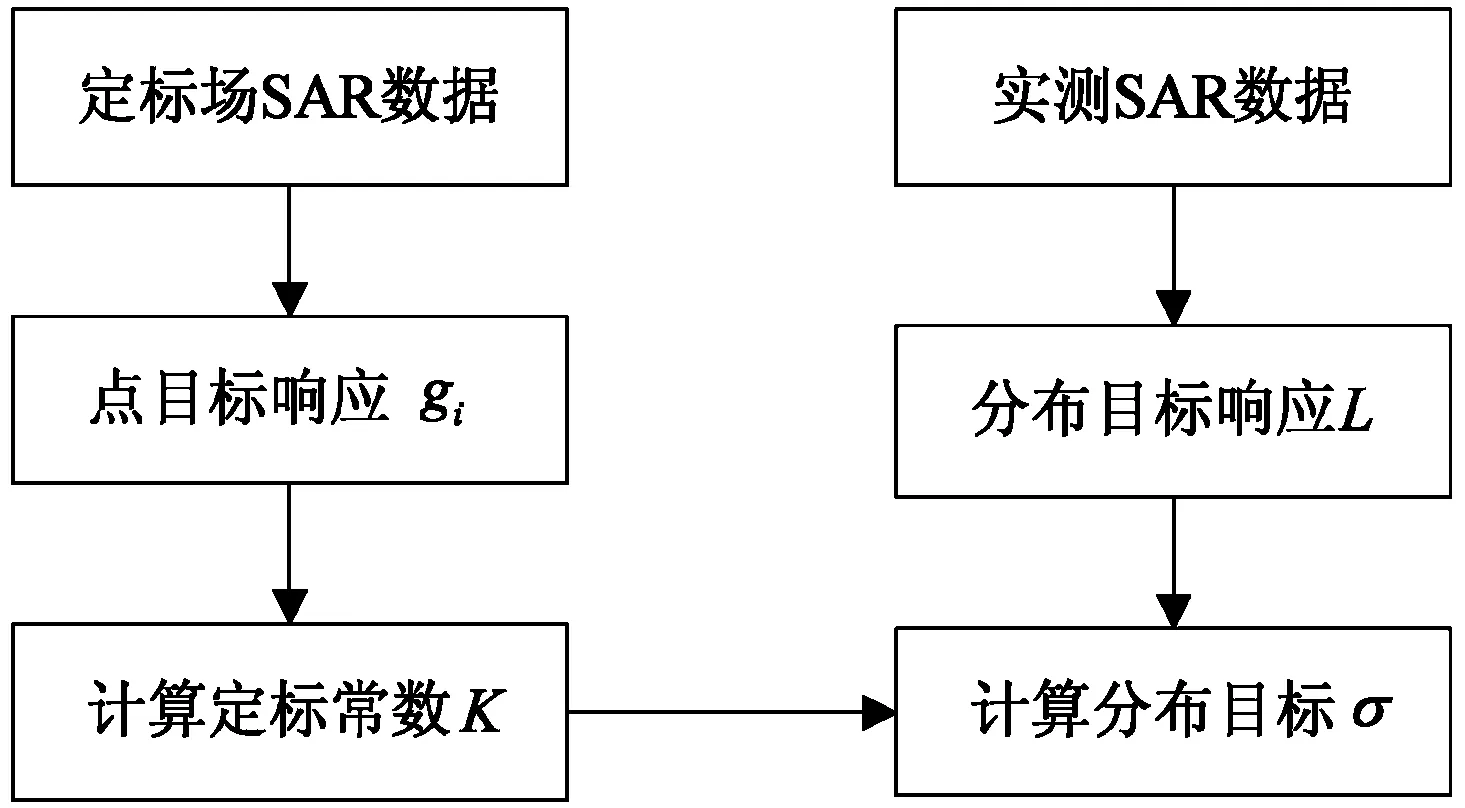
圖6 目標RCS定標流程

為計算定標常數K，共進行n(=5)次測試，設σref為定標器散射截面理論值，則定標常數Ki=gi/σref.為提高定標精度，以5次測試的平均值作為最終定標常數.

實驗設計的三面體角反射器棱長a=0.2 m, 入射波頻率f=9 GHz (波長λ=0.033 m).當固定俯仰角θ=60°，方位角φ在區間[0°,90°]上變化時的RCS曲線如圖7虛線所示.曲線關于φ=45°對稱，RCS在φ=45°處取得較大值.當固定方位角φ=45°，俯仰角θ變化時的RCS 如圖7實線所示，可看出RCS 在θ=56°附近時取得極大值.

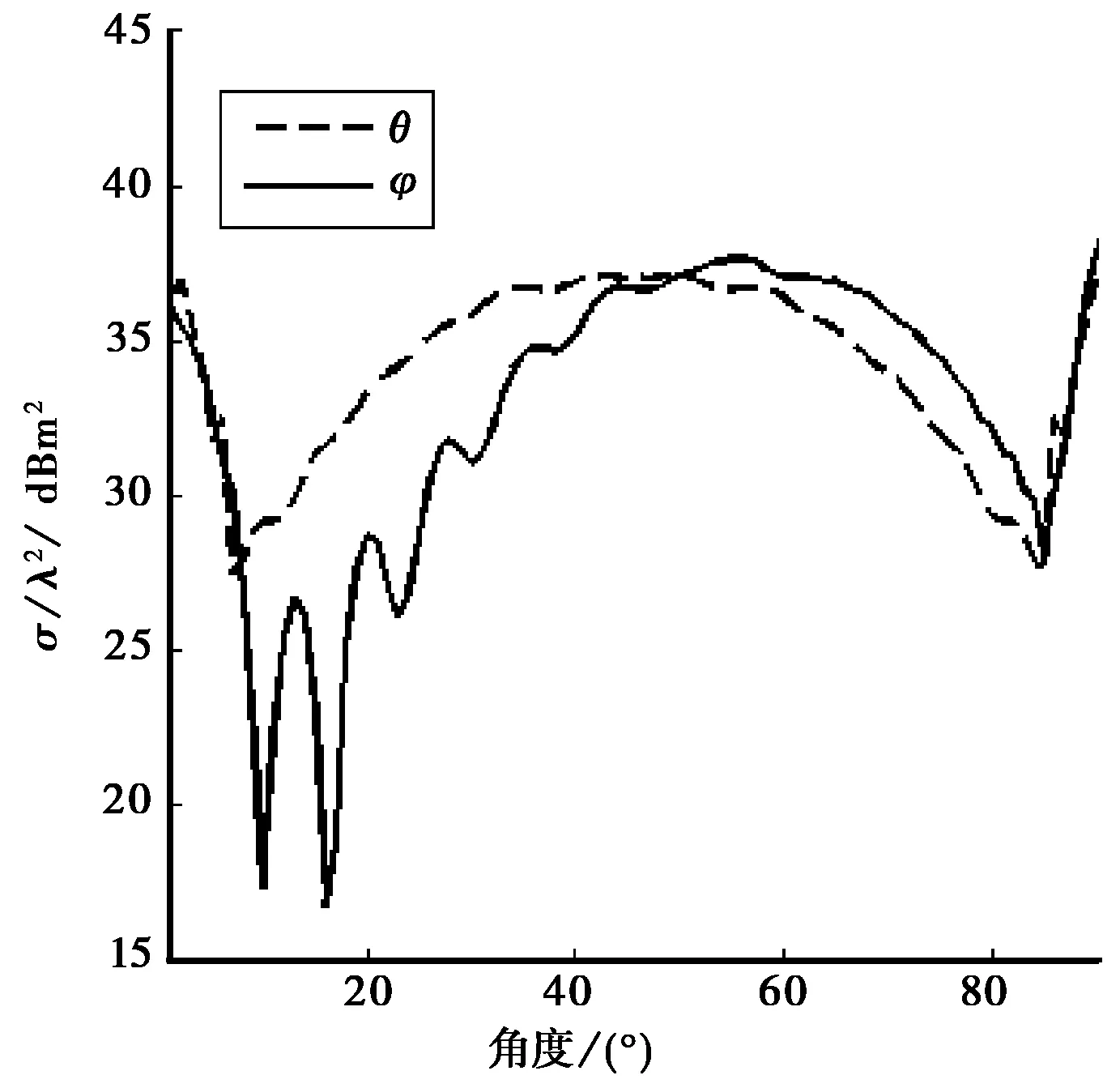
圖7 三面體角反射器RCS

按三面體角反射器RCS[13]最大值公式σmax=4πa4/(3λ2)，目標RCS變化的動態范圍很大，常用其相對的1 m2分貝數來表達，即分貝平方米(dB·m2)，三面體角反射器RCS表示為10log(σmaxλ2)=37.34 dB·m2.

該值與FEKO算法計算(如圖7)的10log(σmax(FEKO)/λ2)=37.63 dB·m2相差很小，精度為0.7%.根據以上定標，實驗室三面體角反射器定標常數確定為K=gi/σref=42.75，定標結果見圖8.

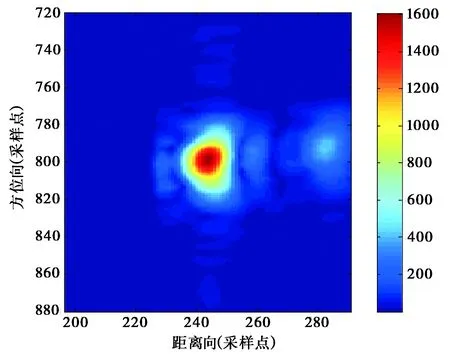
(a) 定標前

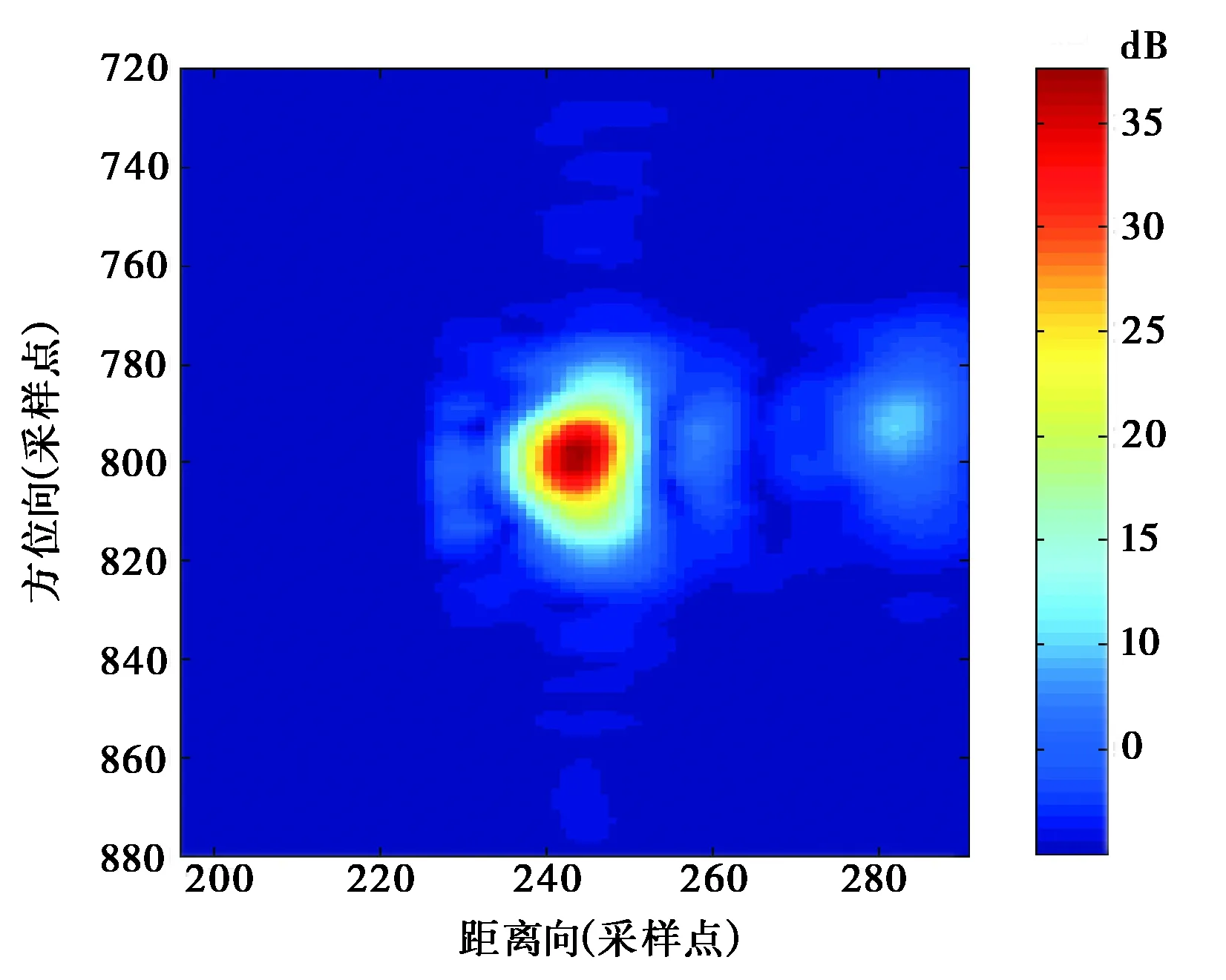
(b) 定標后圖8 三面體角反射器成像

2 目標模型極化散射與成像實驗

移動平臺以場景為中心，以3 cm/s勻速橫向平移1.5 m，天線高度為2 m.坦克模型長約1.1 m，高約0.45 m，寬0.45 m，采用寬帶喇叭天線獲取8～10 GHz的全極化散射矩陣數據[14]，采樣頻率間隔為25 MHz.假設沿信號入射的方向為距離向，與取樣架平行方向為方位向，則方位向和距離向分辨率分別為：ΔR=c/(2Δw)=7.5 cm和L/2=6.9 cm.在多個小球的成像中，當小球間距離低于理論分辨率時在圖像中難以分辨，反之則能分辨，因此，確定了實際成像結果的分辨率和系統參數分析成像分辨率是一致的.考慮SAR成像的幾何特征，斜距圖像的比例失真，透視收縮與頂底位移等特性，在不同的雷達視角下，有不一樣的成像特性.視角分別取0°，10°，30°，如圖9所示.由于實驗室雷達視角的調整區間為10°～60°，在選用0°時，是將坦克模型按天線射線方向傾斜對應的角度.

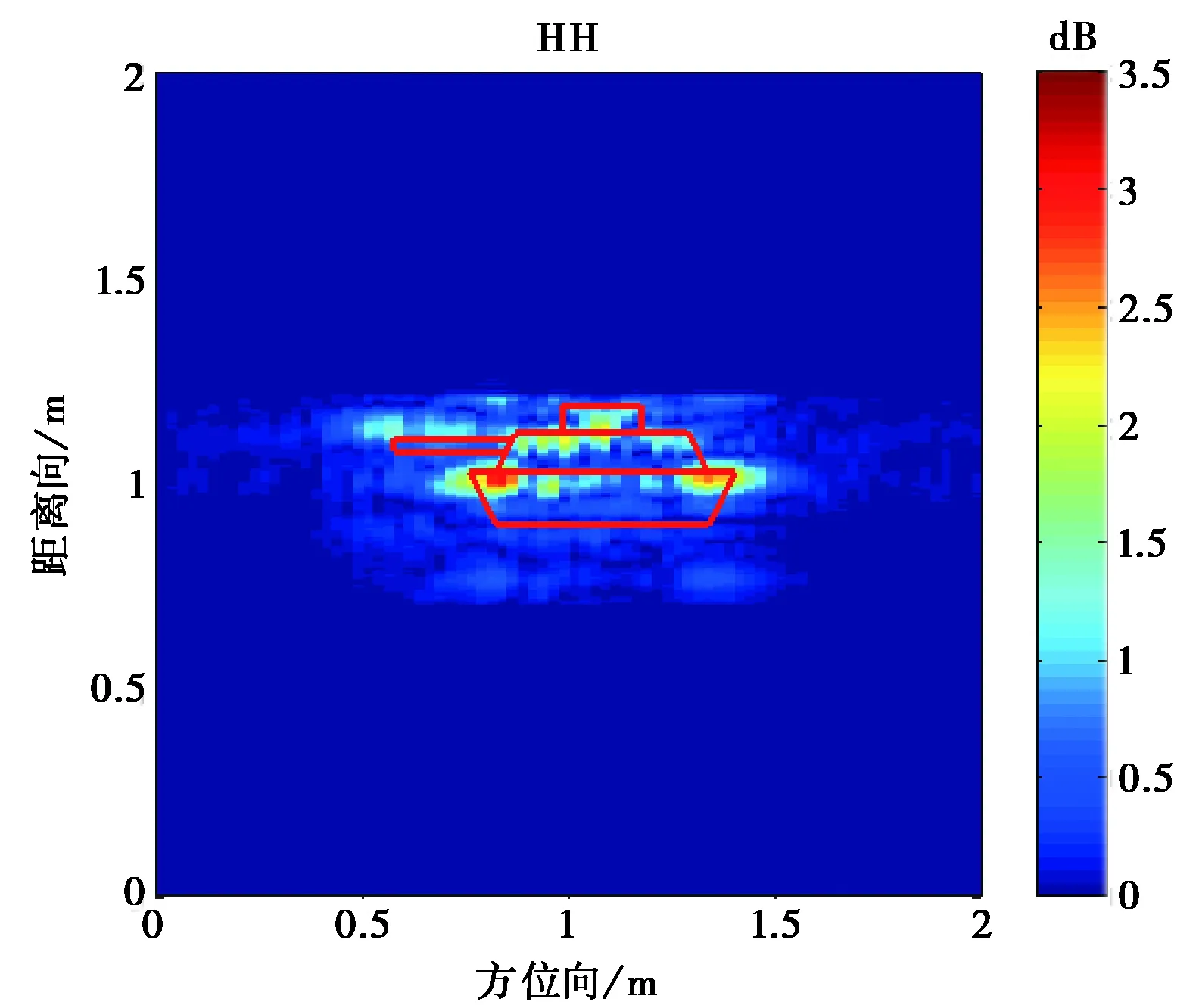
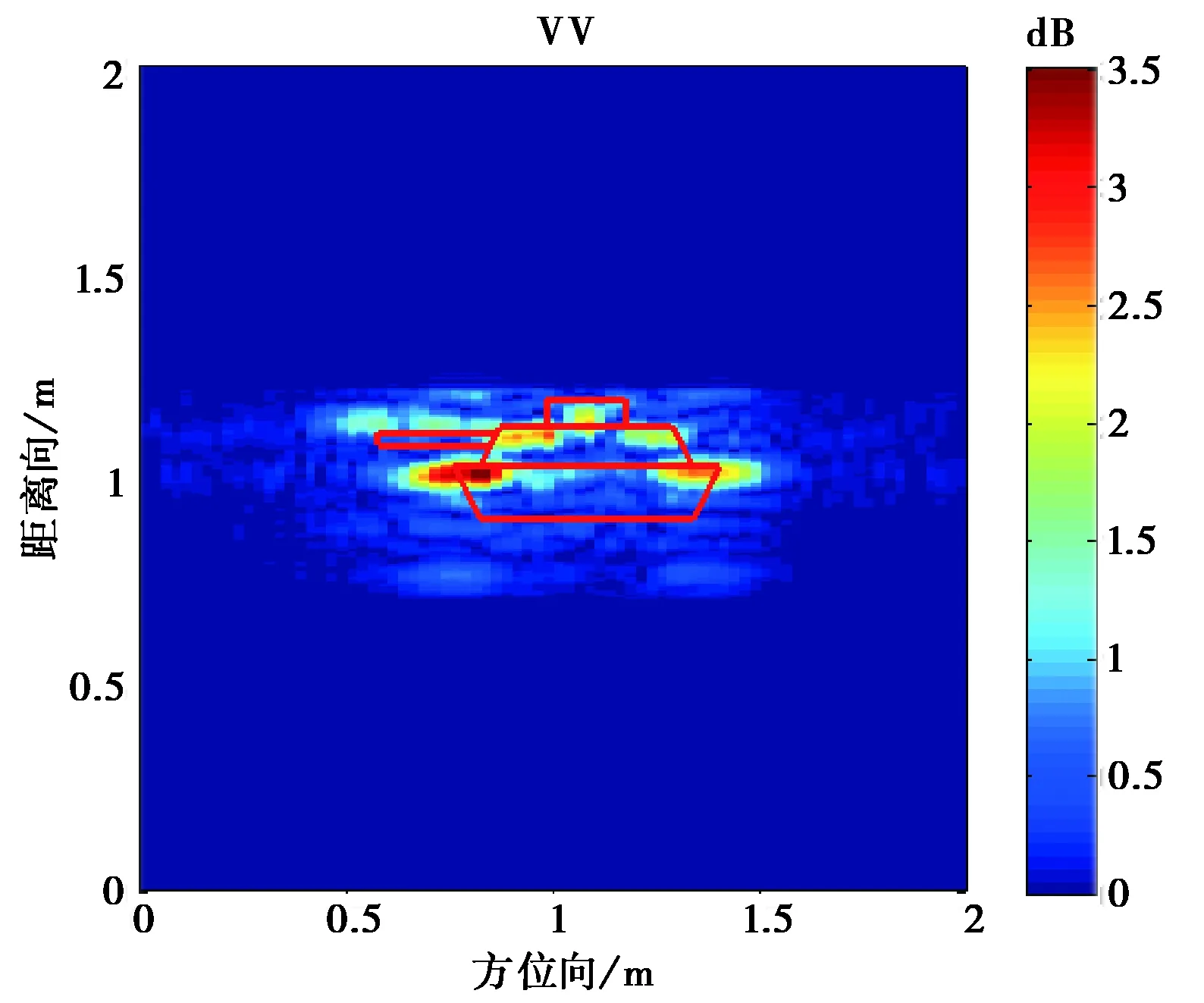
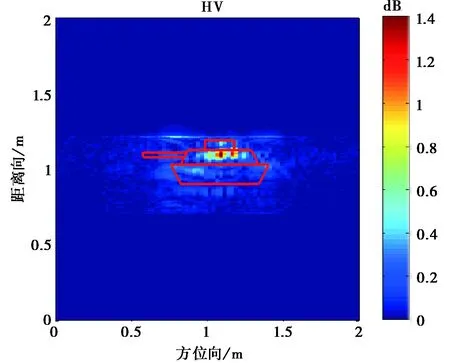
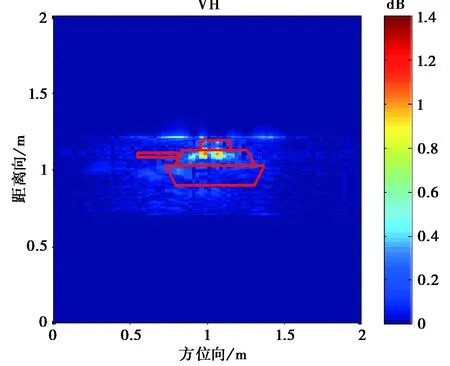
圖10 入射角為0°的坦克模型目標極化成像

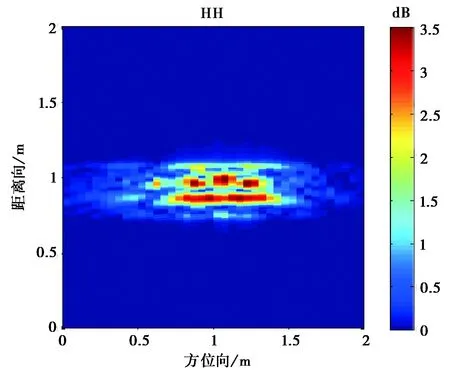
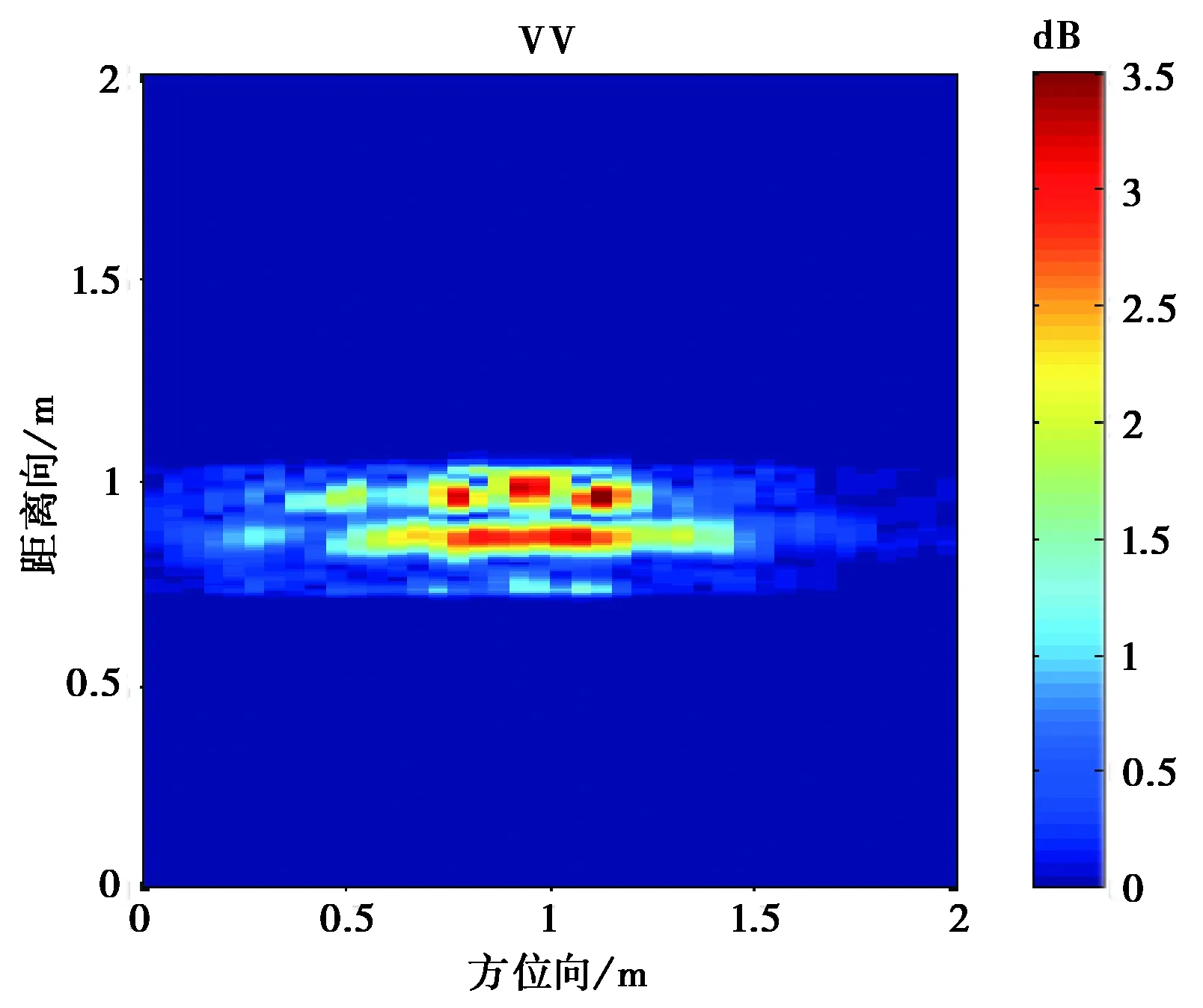
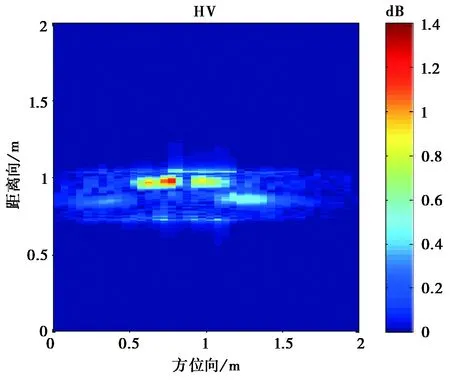
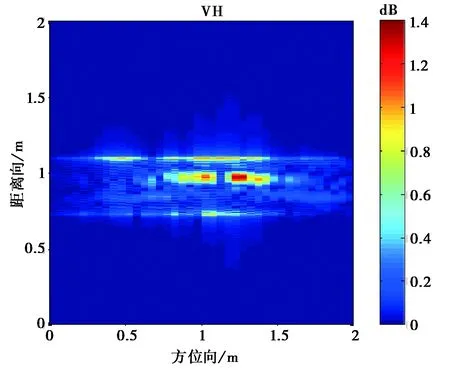
圖11 入射角為10°的坦克模型目標極化成像

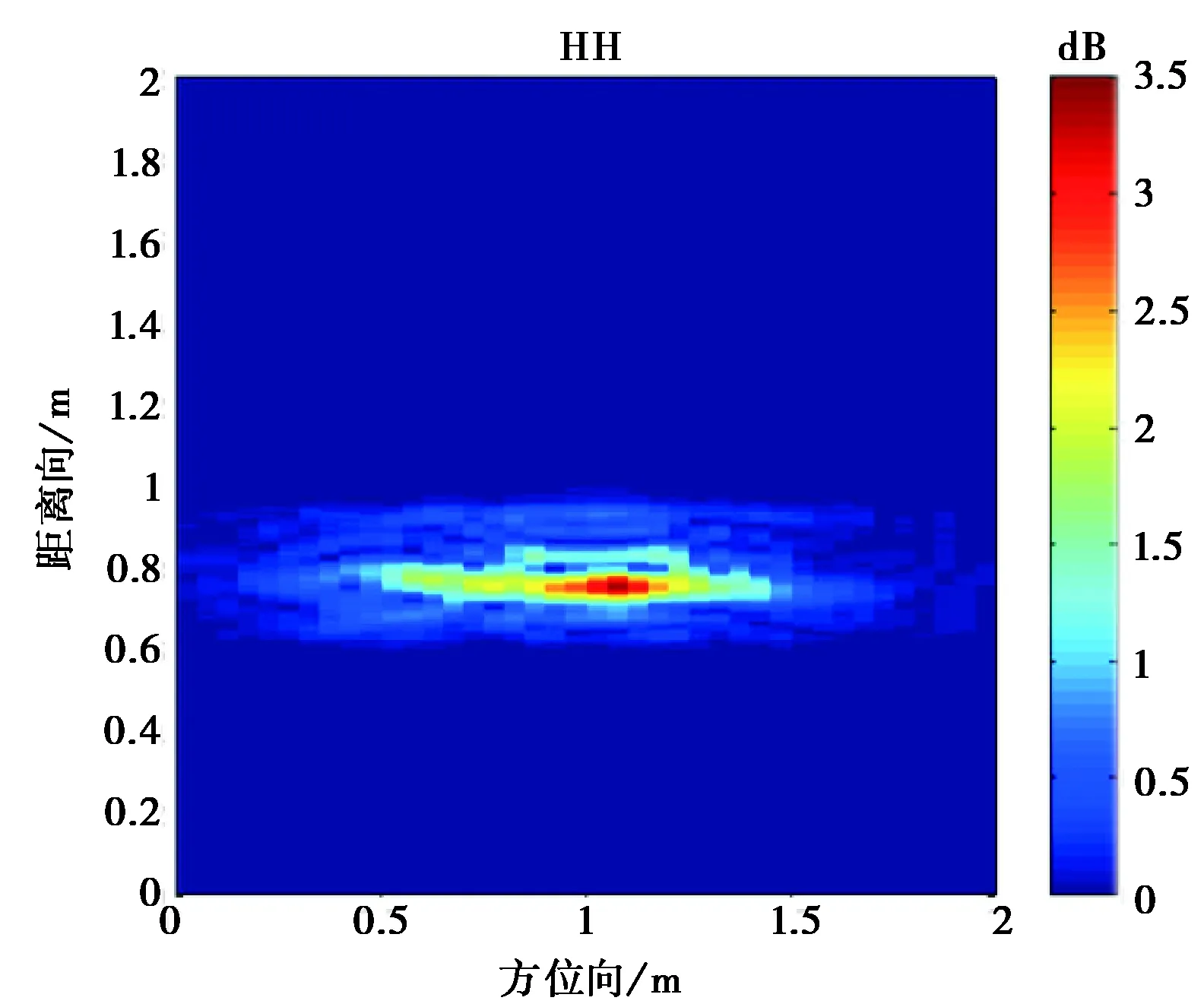
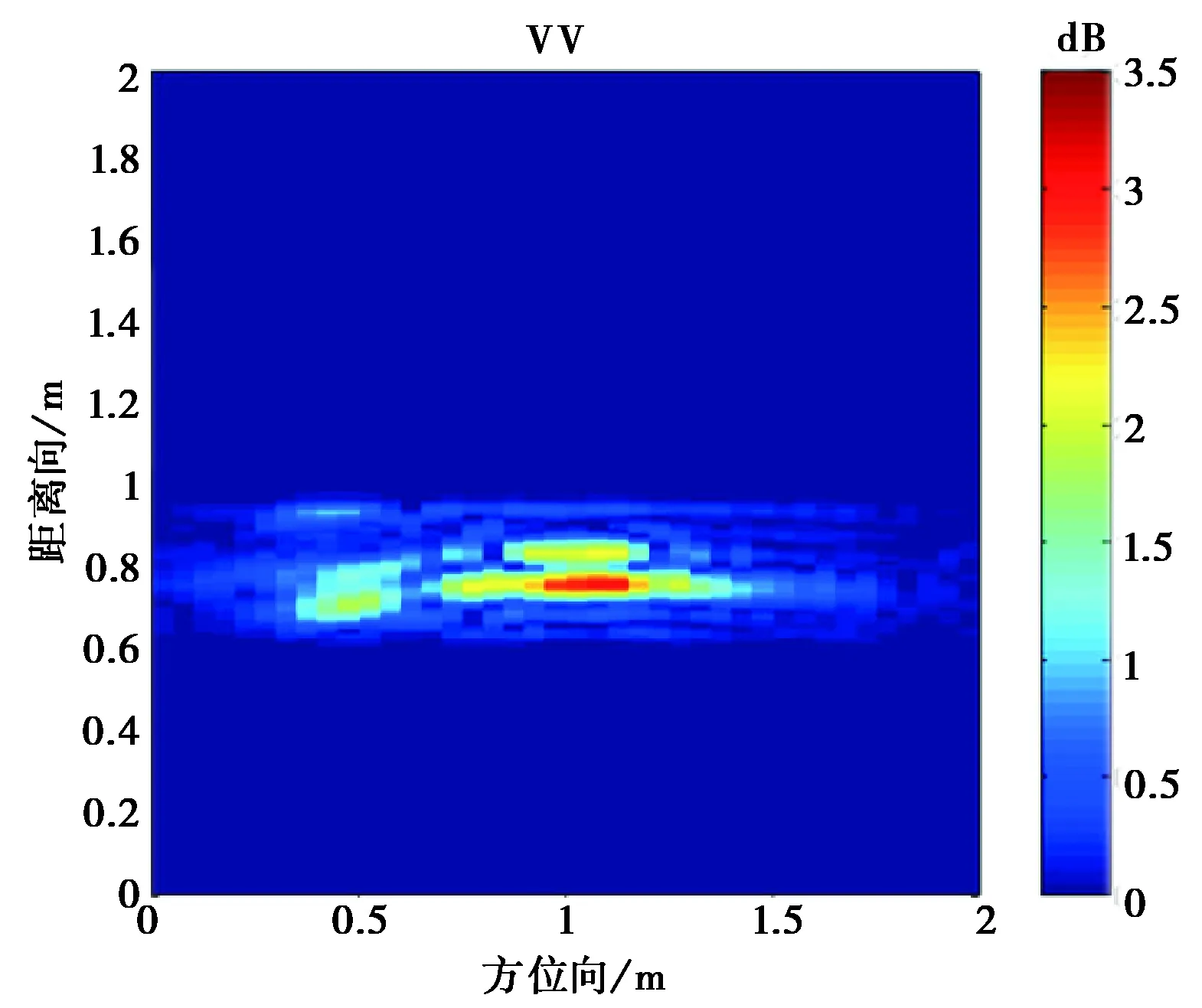
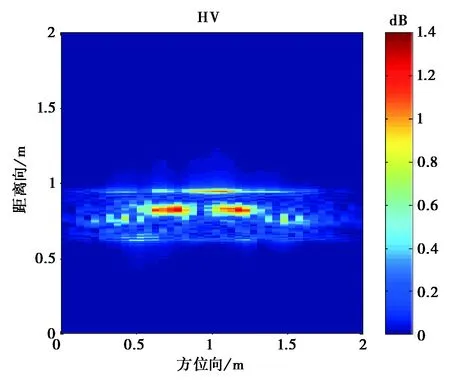
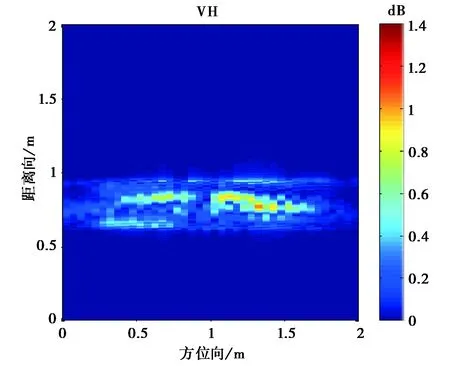
圖12 入射角為30°的坦克模型目標極化成像

從圖10～12成像結果可看到，入射角為0°的時的成像與坦克模型直覺上比較吻合.由于模型表面光滑，鏡面反射很強，使得不同入射角產生的成像結果有比較大的區別.

另外，我們對于樹葉遮蔽下坦克模型的散射也進行了試驗.在樹葉比較稀疏情況下，雷達信號還是能穿過覆蓋的樹葉.可看到，雷達信號有明顯的衰減，而交叉極化卻有一些增強，這是由于樹葉樹枝的散射, 以及樹葉與目標表面的多次散射.

3 FEKO數值計算的驗證

通過FEKO數值計算目標極化散射，對本實驗數據進行驗證.在入射角0°時，用FEKO計算得到的極化散射場HH與HV的成像，結果如圖13所示.

通過對比，數值計算與實驗結果視覺上形狀基本一致，驗證了本實驗.坦克在FEKO中數值計算成像的結果要略大于實驗中坦克成像結果，且在交叉極化的數值結果比實驗結果好.這主要是交叉極化信號弱，實驗中可能的各種干擾會特別影響交叉極化的實驗結果.

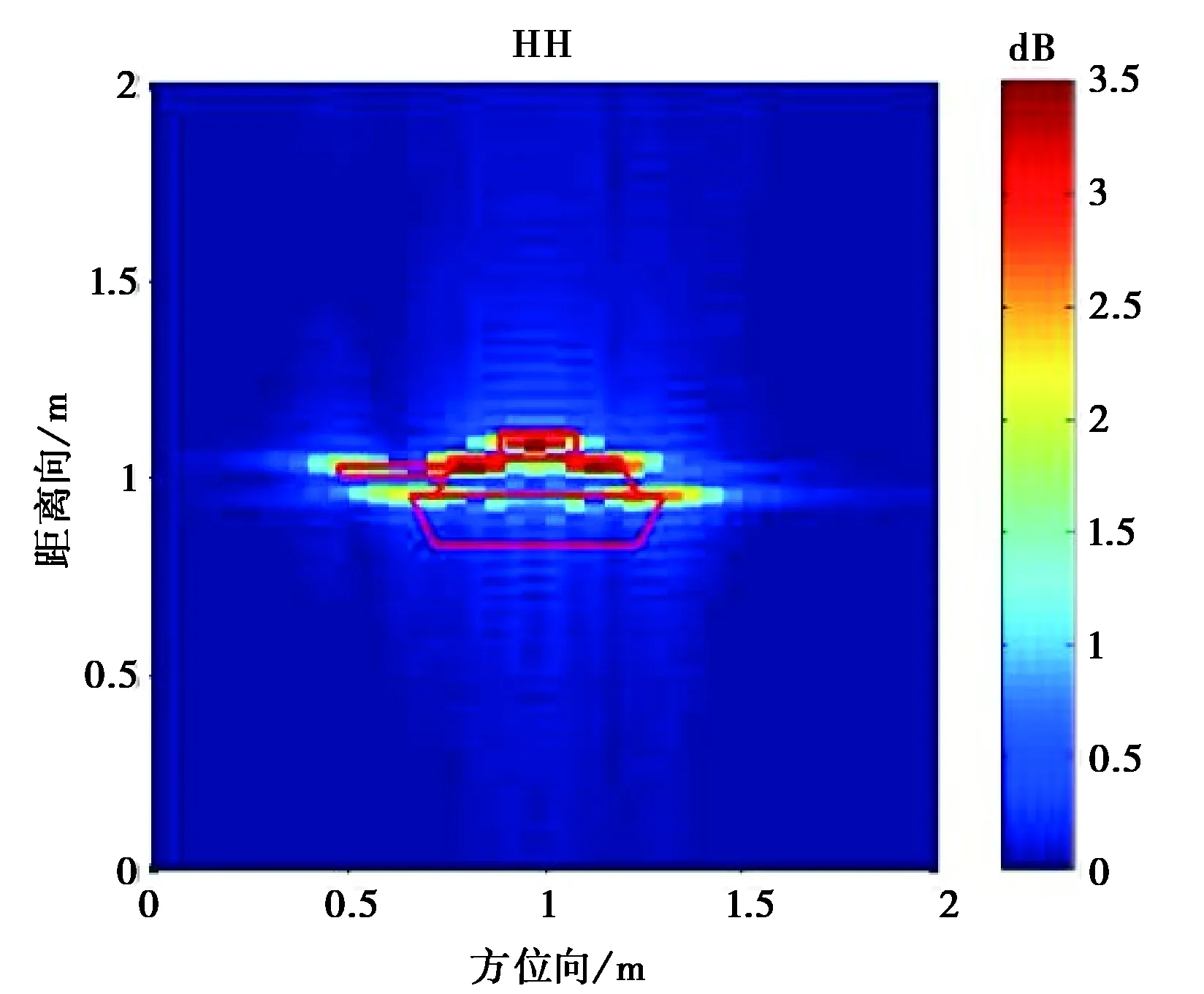
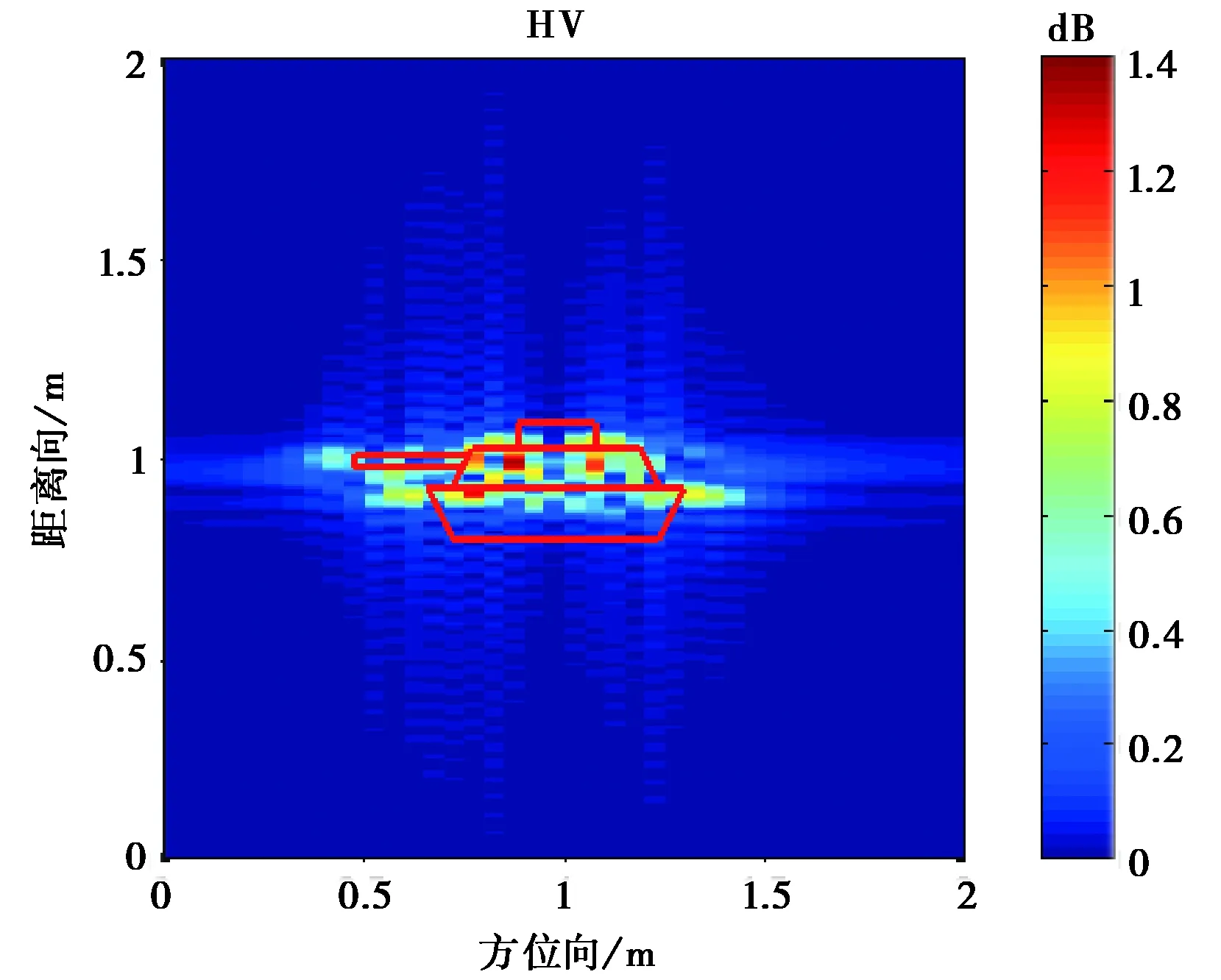
圖13 入射角0°時FEKO數值計算HH,HV散射成像

4 結 論

本實驗室構建了全極化SAR散射成像實驗系統，利用天線平臺的移動合成，測量目標極化散射矩陣，處理得到目標極化二維圖像.

為驗證成像結果，用FEKO數值計算目標的極化散射與成像，比較結果是有意義的.實驗室模擬實驗可有多種實驗設計，模型可靈活選擇.對應的數值計算比較易于進行.另外，對有關內容的教學也大有裨益.

本實驗系統由于種種條件，誤差難以避免.主要誤差包括：采樣周期誤差(采樣率為25 kHz，一個周期內采樣點數可在1 905～1 915之間變化)，運動平臺誤差(運行速度為3 cm/s，平臺軌道的不平衡，導致采樣信號的波動)，以及極化天線之間的相互耦合帶來的誤差等.

[1] OLVER A D, CUTHBERT L G. FMCW radar for hidden object detection[J]. Radar and Signal Processing, IEE Proceedings F, 1988, 135(4): 354-361.

[2] LIAU T F, CARR A G, CUTHBERT LG. Using non-Fourier techniques in signal processing for an FMCW hidden-object detection radar[J]. Electronics Letters, 1986, 22(9): 466-467.

[3] KAPILEVICH B, PINHASI Y, ANISIMOV M, et al. FMCW MM-wave non-imaging sensor for detecting hidden objects[C]// IEEE MTT-S International Microwave Workshop Series on Millimeter Wave Integration Technologies (IMWS). Sitges, September15-16, 2011: 101-104.

[4] FITCH J P. Synthetic Aperture Radar[M]. New York: Springer-Verlag, 1988.

[5] WANG H, JIN Y Q. A novel polarimetric FM-CW radar system for laboratory remote sensing experiments[C]// Proceedings of the 2010 International Symposium on Antennas, Propagation &EM Theory. Guangzhou, November 29-December2, 2010: 662-665.

[6] META A. Signal Processing of FMCW Synthetic Aperture Radar Data[D]. Delft: Delft University of Technology, 2006.

[7] 張 軍, 毛二可. 線性調頻連續波SAR成像處理研究[J]. 現代雷達, 2005, 27(4): 42-45.

ZHANG Jun, MAO Erke. A study on LFMCW signal processing[J]. Modern Radar, 2005, 27(4): 42-45.(in Chinese)

[8] NAKAMURA M, YAMAGUCHI Y. Real-time and full polarimetric FM-CW radar and its application to the classification of targets[C]// IEEE Trans Instrum Meas, 1998, 47(2): 572-577.

[9] YAMAGUCHI Y, NISHIKAWA T, SENGOKU M. Two-dimensional and full polarimetric imaging by a synthetic aperture FM-CW radar[J]. IEEE Trans Geosci Remote Sens, 1995, 33(2): 421-427.

[10] 李海寧, 趙 健, 洪 文, 等. 基于分數傅立葉變換的SAR成像算法研究[J]. 遙測遙控, 2007, 28(1): 20-24.

LI Haining, ZHAO Jian, HONG Wen, et al. SAR imaging algorithm based on fractional fourier transform[J]. Journal of Telemetry, Tracking and Command, 2007, 28(1): 20-24.(in Chinese)

[11] KEEN K M. New technique for the evaluation of the scattering cross-sections of radar corner reflectors[J]. IEE Proceedings, 1983, 130(5): 322-326.

[12] CURLANDER J C, MCDONOUGH R N. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Boston: Artech House, 2005.

[13] FREEMAN A. SAR calibration: an overview[J]. IEEE Transactions on Geoscience and Remote Sensing, 1992, 30(6): 1107-1121.

[14] 胡楚鋒, 許家棟, 李南京, 等. 全極化SAR半實物仿真系統[J]. 系統工程與電子技術, 2010, 32(7): 1537-1539.

HU Chufeng, XU Jiadong, LI Nanjing, et al. Full-polarization synthetic aperture radar hard-in-loop system[J]. Systems Engineering and Electronics, 2010, 32(7): 1537-1539.(in Chinese)

[15] 保 錚, 邢孟道, 王 彤. 雷達成像技術[M]．北京: 電子工業出版社, 2005.