基于微多普勒特征的目標分類

賈守卿 江小敏 夏明耀

(1．北京大學信息科學技術學院，北京 100871；2．電子科技大學電子工程學院，四川 成都 611731)

引 言

微動是指目標或目標部件除質心平動以外的振動、轉動和加速運動等微小運動. 目標的微動，會引起雷達回波的頻率調制，從而產生雷達多普勒效應的旁瓣，并稱其為微多普勒效應[1-3]，它描述了微動激勵的瞬時多普勒，反映了頻率的瞬時特性.

微多普勒現象可被視為目標結構部件與目標主體之間相互作用的結果, 是該雷達目標所具有的獨特特征, 因而對實現目標的分類、識別、成像具有重要意義，在此方面已有大量研究[4-6].

本文討論利用目標的微多譜特征進行分類，采用算法如下：目標的回波由散射中心模擬，經由希爾伯特-黃變換(Hilbert-Huang Transform, HHT)得到各固有模態函數(Intrinsic Mode Function, IMF)的瞬時振幅與瞬時頻率，以其范數作為特征向量，而分類器采用支持向量機(Support Vector Machine, SVM).

1 希爾伯特-黃變換

HHT[7]是一種用于非線性和非平穩時間序列分析的方法，由經驗模態分解(Empirical Mode Decomposition, EMD)和Hilbert譜分析兩部分組成. 其中，EMD根據信號的局部時間特征尺度來進行非線性分解，不但具有良好的多分辨率分析的特點，而且克服了諸如小波變換之類方法中需要選擇基函數的困難，具有自適應性，因而得到了廣泛應用.

EMD是將多分量信號s(t)分解為有限個IMFci(t)(1≤i≤N) 與殘差項r(t)，即

(1)

IMF是滿足下列兩個條件的單分量信號：

1) 零點數與極值點數相等或至多相差1；

2) 信號上任意一點，由局部極大值點確定的包絡線和由局部極小值點確定的包絡線的均值為0.

關于EMD的步驟簡要介紹如下：首先確定出s(t)的所有極值點，然后將所有極大值點和所有極小值點分別用一條曲線擬合起來，使兩條曲線間包含所有的信號數據. 將這兩條上、下包絡線的平均值記作m，令h=s-m，將h視為新的s，重復以上操作，直到h滿足某種終止條件(如h變化足夠小) 時，記c1=h，即為第一個IMF. 再令r=s-c1，將r視為新的s，重復以上操可依次得其余的IMF，當r滿足給定的終止條件(如r足夠小或成為單調函數)時，分解過程結束.

對IMF做Hilbert變換，可得解析函數為

zi(t) =ci(t)+jH[ci(t)]

=Ai(t)exp[jφi(t)] .

(2)

式中:H[·]表示Hilbert變換;Ai(t)為振幅；φi(t)為相位. 對相位φi(t)求導可得瞬時頻率為

(3)

取Nc(≤N)個IMF瞬時振幅與瞬時頻率的范數構成特征向量為

x=[‖A1‖…‖ANc‖‖f1‖…‖fNc‖]T.

(4)

2 支持向量機

支持向量機[8]是針對分類和回歸問題的統計學習理論. 由于SVM方法具有許多引人注目的優點和有前途的實驗性能，越來越受重視，該技術已成為機器學習研究領域中的熱點. 下面簡單介紹用于分類問題的SVM算法.

設訓練樣本為(xi,yi)(i=1,2,…,Ns)，其中xi是目標的特征向量，yi=±1表示兩種判決結果. 對于待判決目標的特征向量x，SVM的判決輸出f(x)由下式給出：

(5)

(6)

式中:K(·，·)是核函數，這里采用高斯形式

(7)

式中:‖·‖是向量范數；SV是支持向量集，即滿足αi>0的樣本集； |SV|是支持向量個數；αi是下面約束優化問題的解為

(8)

約束條件為

(9)

若目標多于兩個，可用多個SVM，以其輸出的二進制組合標識目標. 例如有8個目標，則用3個SVM，如圖1所示，以組合(y1y2y3)標識目標.

圖1 3個SVM組合

3 算 例

目標回波可用散射中心模擬

(10)

ri(t)=Rz(2πfpt)·Ry(θp+θmsin2πfbt)

(11)

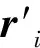
式(11)的微動參數如圖2所示.

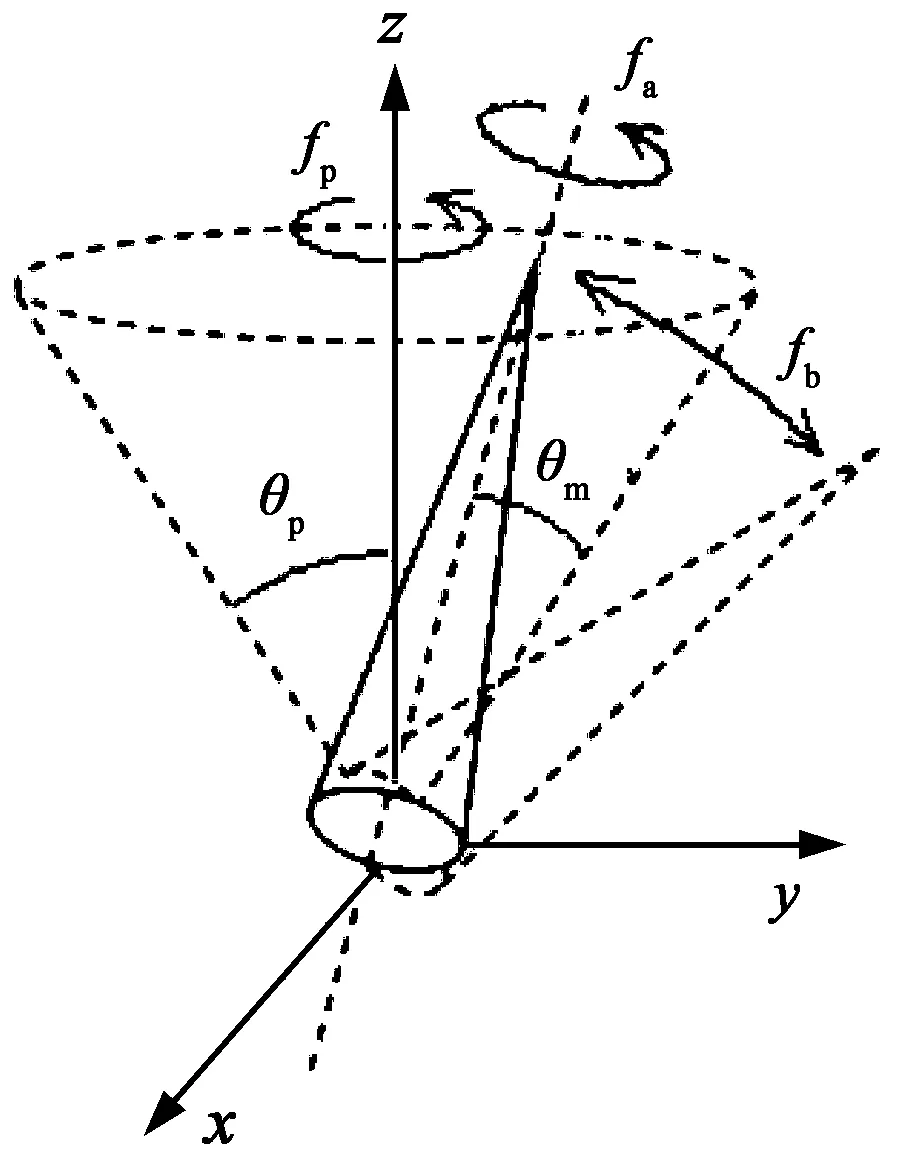
圖2 微動目標示意圖

表2 微動參數

σ=ξNx.

(12)

式中Nx是無噪聲下各目標特征向量的平均范數. 分別取ξ=0.01，0.05，0.1，在不同信噪比環境下的識別率如圖4所示.

圖4 識別率與信噪比的關系

由圖4可以看到：取合適的核函數參數(本例取ξ=0.01～0.1)，在較低的信噪比條件下也可取得很高識別率.

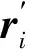
圖5 8個虛擬目標的散射中心分布

坐標r′i1(0，0，2)(0，0，1)(0，0，0)(-1，0，-1)(1，0，-1)2(0，0，1．8)(0，0，0．6)(0，0，-0．5)(1，0，-0．5)(-1，0，-0．5)3(0，0，2)(0，0，1)(0，0，-0．5)(1，0，0)(-1，0，0)4(0，0，1．5)(0，0，0．5)(0，0，-0．5)(-1．2，0，0．5)(1．2，0，0．5)5(0，0，2)(0，0，0．5)(0，0，-0．5)(1．5，0，0．5)(-1．5，0，-0．5)6(0，0，2．2)(0，0，0．6)(0，0，-0．4)(1．3，0，2．2)(-1．3，0，-0．4)7(0，0，2)(0，0，1)(0，0，0)(1，0，1)(-1，0，-1)8(0，0，2)(0，0，0．9)(1，0，0)(-1，1，0)(-1，-1，0)

表4 散射強度

表5 微動參數

截取IMF個數Nc=5，其他參數同例1. 式(12)中的參數ξ分別取0.008，0.01，0.1，0.2，在不同信噪比環境下的識別率如圖6所示.

圖6 識別率與信噪比的關系

由圖6可以看到：取合適的核函數參數(本例為ξ=0.01～0.1)，在較低的信噪比條件下也可取得較高識別率，這得益于支持向量機的優秀泛化能力，即避免小樣本的過度擬合.

4 結 論

通過對微動目標回波進行經驗模態分解，再對固有模態進行希爾伯特-黃變換，以固有模態的幅度和頻率的范數作為特征向量，再用支持向量機進行分類識別，在較低信噪比環境下取得了較高的識別率.

[1] CHEN V C, LI F, HO S S, et al. Analysis of micro-Doppler signatures[J]. IEE Proc Radar Sonar Navig, 2003, 150(4): 271-276.

[2] 李 松. 基于壓縮感知的彈道導彈微多普勒提取方法[J]. 電波科學學報, 2011, 26(5): 990-996.

LI Song. Extraction of micro-Doppler of ballistic missile based on compressive sensing[J]. Chinese Journal of Radio Science, 2011, 26(5): 990-996. (in Chinese)

[3] 楊 儉, 侯海平. 機載下視陣列合成孔徑雷達成像的微多普勒效應[J]. 電波科學學報, 2012, 27(5): 1049-1055.

YANG Jian, HOU Haiping. Micro-Doppler effect for airborne downward-looking array SAR imaging[J]. Chinese Journal of Radio Science, 2012, 27(5): 1049-1055. (in Chinese)

[4] 關永勝. 基于微多普勒特征的空間錐體目標識別[J]. 電波科學學報, 2011, 26(2): 209-215.

GUAN Yongsheng. Micro-Doppler signature based cone-shaped target recognition[J]. Chinese Journal of Radio Science, 2011, 26(2): 209-215. (in Chinese)

[5] KEALEY P G, JAHANGIR M. Advances in Doppler recognition for ground moving target indication[J]. Proc SPIE, 2006, 6234: 62340W.

[6] SMITH G E, WOODBRIDGE K, BAKER C J. Micro-Doppler signature classification[C]//Proc CIE Int Conf Radar. Shanghai, October 16-19, 2006: 1-4.

[7] HUANG N E, SHEN Z, LONG S R. The empirical mode decomposition method and the Hilbert spectrum for non-stationary time series analysis[J]. Proc Royal Soc London A, 1998, 454 (A): 903-995.

[8] BURGES C J C. A tutorial on support vector machines for pattern recognition[J]. Data Mining and Knowledge Discovery, 1998, 2(2): 121-167.

[9] 代大海, 王雪松, 莊順平, 等. 全極化散射中心提取參數估計: P-MUSIC方法[J]. 信號處理, 2007, 23(6): 818-822.

DAI Dahai, WANG Xuesong, ZHUANG Shunping, et al. Fully polarized scattering center extraction and parameter estimation: P-MUSIC algorithm[J]. Signal Processing, 2007, 23(6): 818-822.(in Chinese)