對“后課標時代”數學教學鋪墊的探析

毛新薇

進行課程改革十多年，有關數學教學的很多理念得到了較好的落實，數學課堂教學也發生了巨大的變化。但在欣喜之余，我們不無遺憾地發現，部分教師盲目追求形式上的“新理念”，以“新舊”代替“好壞”，致使課堂教學局限于一種“低層次的摸索”。修訂后的《 義務教育數學課程標準 》正在實施（這里暫且稱為“后課標時代”），在“后課標時代”重新審視當前數學課堂中鋪墊方面存在的問題，理性思考鋪墊的價值訴求，賦鋪墊以新理念、新認識、新內涵，顯得十分重要。

一、審視——對當前課堂中鋪墊問題的詰問與考量

詰問一：“后課標時代”，我們還需要鋪墊導入嗎？

自新課程實施以來，教材上很少安排復習鋪墊，情境教學開展得如火如荼。然而稍加留意，我們就能發現許多教師關注的不是學習內容本身，而是如何挖空心思創設情境，數學教學變得流于形式，失去了數學味。

南京師范大學涂榮豹教授曾說過：“中國的數學教學長于由‘舊知引出‘新知，絕大多數‘新知是由‘舊知引入的，這基本符合人的認識規律，也與現代認知主義理論、建構主義思想一致。”適時、適度、適可的鋪墊導入是完全必要的，好的鋪墊導入可以恰到好處地激活學生的知識“固著點”與“生長點”，為學習新知提供有力的支撐，幫助學生通過遷移而同化或順應原有的認知結構，降低學習難度。值得注意的是鋪墊不能限制學生的思維，而應該喚醒學生的積極思維，讓他們主動參與到探索新知的活動之中。我們可以融鋪墊導入和情境創設為一體，實現兩者的和諧統一，這正是對傳統意義上鋪墊導入的繼承與創新，也是鋪墊策略在“后課標時代”的一種新走向。

詰問二：“后課標時代”，我們何時進行鋪墊？

進行課程改革之前，教師在教學中很重視鋪墊，課堂教學多以復習提問的形式開始，導致學生有能力獨立探究的，也被教師鋪墊所代替了，走向了極端。進行課程改革之后，情境創設成了寵兒，本該需要的鋪墊被情境所代替，導致學生探究活動時的茫然，走向了另一種極端。究其原因，主要是教師對何時鋪墊心中無數。

鋪墊應該鋪在該鋪時。何為該鋪時？其實這是由學生探究活動時的“潛在距離”來決定的。學生學習時，所探究的問題與知識固著點存在著不同的“潛在距離”，影響著探究活動的難易程度。一般來說，當兩者的“潛在距離”較小或者適中時，學生就有能力自主構建，這時就沒必要安排鋪墊，但當兩者的“潛在距離”較大，學生已有的舊知識不足以引導學生發展新的知識與認知結構時，大多數學生就需要教師幫助他們在新舊知識之間架設一座“認知橋梁”，來調節新舊知識的“潛在距離”，這時就需要一定的鋪墊。

詰問三：“后課標時代”，鋪墊有哪些新的內涵？

作為課堂教學中的一個范疇，鋪墊在不同的時期應具有不同的意義與價值。尤其是在“后課標時代”，鋪墊應該賦予新的時代內涵。它除了傳統意義上的基于舊知認知、基于經驗認知、基于方法滲透、基于情感渲染等形式外，正體現著一種新思維貫穿于教學的整個過程之中。課堂上，教師如果能提供學生充分的自主探究的時間與多維互動的交流空間，就能讓新知的形成自然生長于豐富的過程中，讓“鋪張”有度的過程“鋪墊”出豐富多彩的結果。從這個意義上講，學生的整個探究過程就是另一種形式上的鋪墊。

另外，除固定課時外，我們還用系統的視角來審視鋪墊，把鋪墊放到更廣更高的視野來認識。因為學生學習數學的過程是其認知結構不斷建構、趨于完善的系統化、結構化、整體化的過程，過程中的前一個認知活動都是后一個認知活動的基礎和準備，后一個認知活動都是前一個認知活動的發展與再建構，因此，從整體意義上講，每一個認知活動的完成都是為了下一個認知活動的開始作鋪墊，這是一種整體的鋪墊觀。

二、深入——“后課標時代”數學鋪墊的有效踐行

1.導入式鋪墊——未成曲調先有情

進行鋪墊的前提是教師要準確把脈學生的知識基礎、經驗和思維水平，量準學生探究問題與原有知識結構之間的“潛在距離”，幫助學生清晰“固著點”，有效地實現新知的自我構建。在教學中，教師通過課前測試、學生訪談、專項調查等途徑可以了解學生真實的學習困惑，探明學生的“潛在距離”。

【案例】用前測把好學生認知之脈

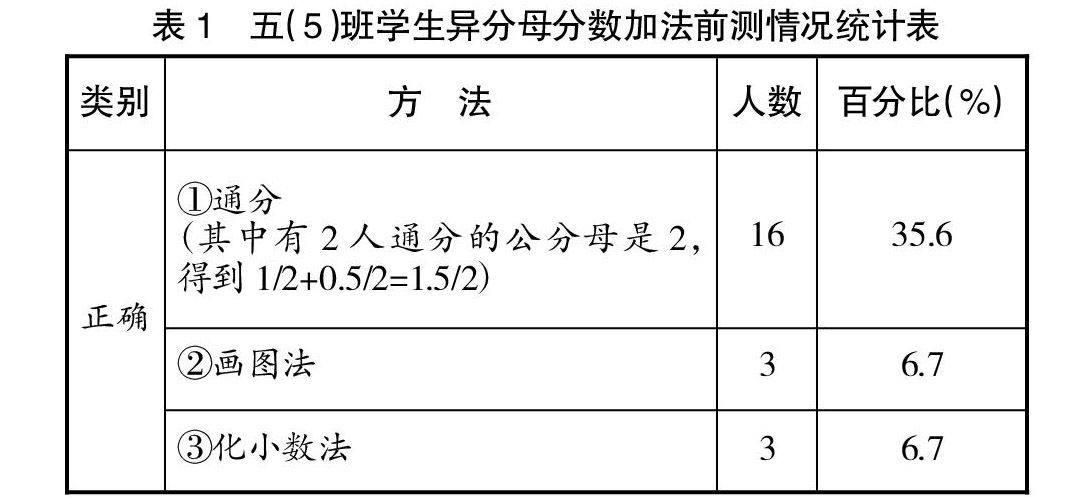
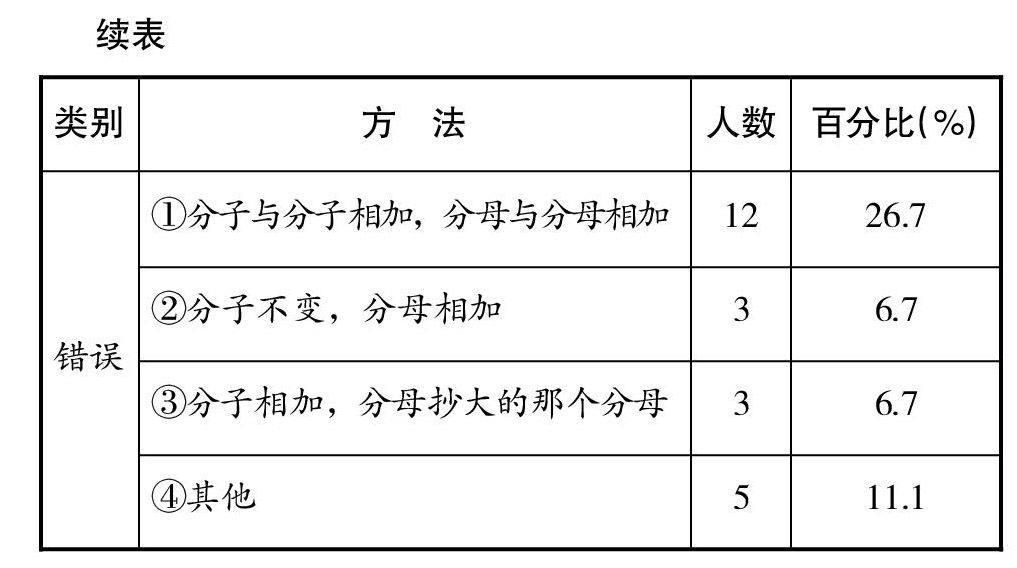
在教學《 異分母分數加減法 》之前，我進行了前測，出了嘗試題“1/2+1/4=？”，讓學生進行嘗試練習，前測結果見表1。

全班45人，運用通分法計算正確的占35.6%，運用畫圖法計算正確的占6.7%，運用化小數法計算正確的占6.7%，正確率達48.9%。從前測結果分析，學生的學習起點是有顯著差異的。異分母分數加減法這一知識的固著點是整數、小數、同分母分數加減法的計算方法、算理（明確只有計數單位相同才能相加）及通分。有一部分學生在從已有知識和經驗到解決新問題之間存在著“潛在距離”，而且每個人的“潛在距離”有長有短，教師既要通過鋪墊舊知，還要為學生設計不同的探究路徑。

我展開了這樣的鋪墊：① 復習通分。② 復習整數、小數、同分母分數加減法的計算方法。③ 明確算理，只有計算單位相同才能直接相加。④ 讓學生討論探究異分母分數加減法，思考：根據計算單位相同才能直接相加的道理，想一想怎么計算異分母分數加減法？如果不能直接解答的，可以借助學過的解決問題的策略如畫圖、轉化等來思考；如果有困難的，可以打開課桌里老師準備的導學單。這樣，通過相關舊知識的復習，幫助學生實現了基本知識與基本技能的遷移，為接下來的探究提供了有力的支撐。讓學生自由選擇不同的方法，既尊重了學生的客觀差異，又滿足了不同學生的學習需求，讓所有的學生都能進行符合自己學習水平的探究。

2.過程性鋪墊——春風化雨潤無聲

顧泠沅教授曾指出：“優秀教師始終把能有力推動學習前進的適度序列視為課堂教學的生命線。”數學活動過程的基本特性是層次性，這種層次性可以表現為一系列的臺階。基于過程的鋪墊要求教師根據各個階段知識內容確定最佳結構以及這些結構之間呈現合適梯度的最佳序列。

【案例】以梯度建構促數學理解

平行線的畫法是教學的難點，一位教師在教學本環節時，精心設計了合適的梯度序列，引發學生思考：① 摸底。你準備怎樣畫平行線？（想到描和移，但發現用移的方法容易變歪）。② 質疑。怎樣移畫出來的就一定是原直線的平行線呢？（學生感到困惑無助）③ 原型啟發。（觀看紗窗平移）是什么保證窗戶邊平移前后所在的直線一定互相平行？（靠著軌道滑行）④ 移植。能不能在畫平行線時也安裝個軌道，讓它有個依靠？怎么安裝？安裝時要注意什么？⑤ 定位。畫平行線時要經歷哪些步驟（對、靠、移、畫）？從“為什么要靠”到“用什么靠”，再到“怎么靠”，構成了一條主題鮮明、各環節相融、對話引證的適度序列。在這一系列的前進序列過程中，前一問題為后一問題的探究提供了無痕鋪墊，這一連串的問題解決過程其實就是一個逐步深入、層層遞進的分層建構過程，在這種合適序列的演變過程中，學生對平行線畫法的理解不斷向縱深推進。

3.系統性鋪墊——向青草更青處漫溯

小學數學教材本身很注重邏輯性與層次性，很好地體現了鋪墊的教學思想。如果把教材鋪墊看作是第一次鋪墊，那么教學實踐鋪墊則是第二次鋪墊。從教材鋪墊到教學實踐鋪墊的轉化，需要教師從系統的角度來思考，認清各類知識的來龍去脈和縱橫聯系，創設數學內部前后聯系交匯的情境，讓學生積累前后聯系的經驗，促進其主動建構能力的提高，同時適時適當地滲透后繼知識，為后繼學習埋下伏筆，促進學生的可持續發展。

【案例】讓知識包中的關鍵點更具生長的力量

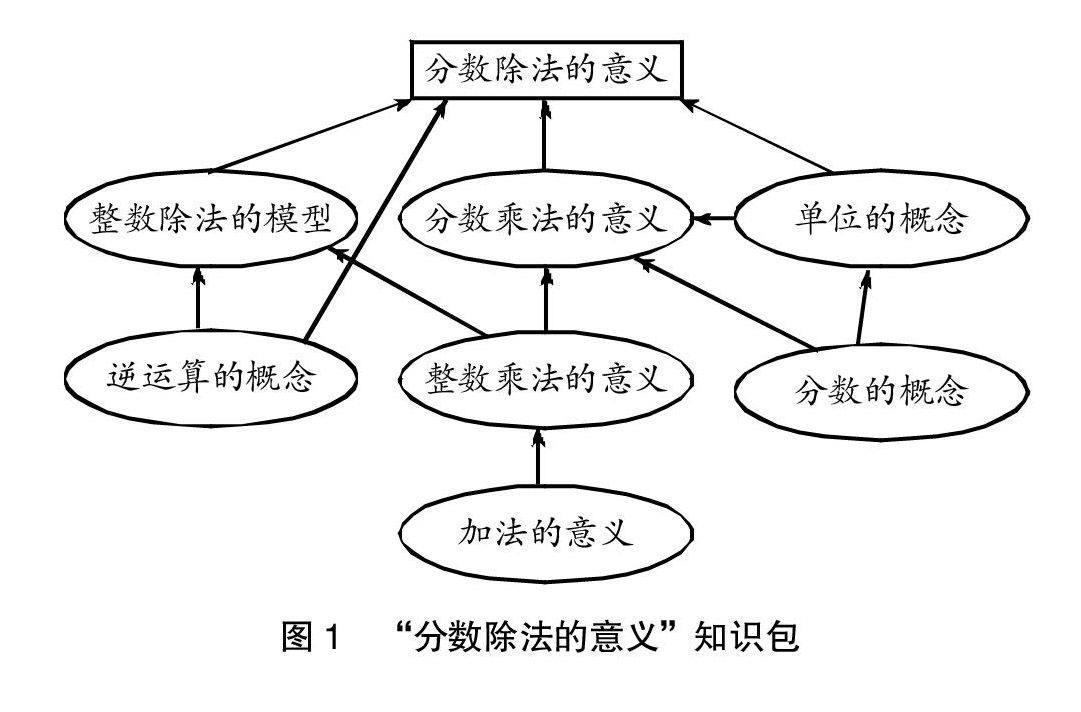
在教研活動中，我們站在系統的角度對“分數除法的意義”進行了研討，梳理出與此相關的幾個重要的知識點：整數乘法的意義、作為乘法逆運算的除法概念、分數乘法的意義、分數的概念、單位的概念等，根據它們之間的關系組建了知識包（見圖1）。

通過研討我們一致認為：分數乘法的意義是知識包中最關鍵的一點，因為它對分數除法的支持力度最大，同時它又處在多個數學概念交叉口上，像一個“結”，將其他多個重要的概念“系”在了一起，聯系了一批支持分數除法意義理解的概念。

分數除法的意義包括兩種模型：包含模型與等分模型，其中分數乘法意義中的“求一個數的幾分之幾是多少”是理解分數除法等分模型“已知一個數的幾分之幾是多少，求這個數”的堅實的“固著點”與生長點。要教好分數除法的意義，分數乘法的意義是關鍵。于是在教學實踐過程中，我們站在系統的角度，對“求一個數的幾分之幾是多少”這一知識點進行了精雕細琢，不僅讓學生會解答“求一個數的幾分之幾是多少”的具體問題，而且進一步與整數乘法中“求一個數的幾倍是多少”溝通聯系，加深學生對分數意義的理解，讓這種對分數乘法本質意義深層次的認識為后續分數除法意義的學習積蓄生長的能量。

“后課標時代”的鋪墊已不再是傳統意義上的某個固定教學時段的一個環節、一種形式、一種手段，而是貫穿于整個小學過程的一種意識、策略與過程。鋪墊在小學數學教學中承載著十分重要的價值，我們將以更廣闊的視野來研究，讓它在“后課標時代”更加濃墨重彩，體現其應有的價值。

（作者單位：江陰市徐霞客實驗小學，江蘇 江陰，214406）