變導程螺旋傳動曲面建模與過渡螺旋線設計

張 威，史 翔，李東波

（1. 南京理工大學 機械工程學院，南京 210094；2. 南京工程大學 機械工程學院，南京 210094）

變導程螺旋傳動曲面建模與過渡螺旋線設計

張 威1，史 翔2，李東波1

（1. 南京理工大學 機械工程學院，南京 210094；2. 南京工程大學 機械工程學院，南京 210094）

0 引言

傳統絲桿只能進行不變導程的螺旋傳動，絲桿的轉動與螺母的直線運動保持嚴格的線性關系。為了使螺母運動速度達到設計人員的具體要求，只能通過對驅動絲桿電機進行轉速的設計。即使這樣，也不能精確滿足螺母運動變化要求。在這樣的情況下，變導程螺旋傳動機構被提出，實現了絲桿轉動與螺母平動的非線性關系，并且經過長期的試驗和設計，目前在地鐵上已經得到了初步應用。

在國內，對變導程螺旋傳動副的研究只是剛剛起步，國外已經有學者對變導程螺旋傳動進行了相關研究。Ming J. Tsai[1]對變導程螺旋傳動機構的傳動效率進行了評價分析。Yan 和Cheng[2]對傳遞滾子的曲面輪廓進行了相關研究。Chiou[3]研究了變導程螺旋傳動的動態特性從理論上進行了分析。本文主要針對單滾子螺旋傳動機構嚙合曲面進行數學建模，并針對螺旋曲面進行設計。

1 螺旋面方程

在工業生產中，絲杠螺紋最常用的加工工藝是銑削加工，本節不考慮加工誤差問題，而是把重點放在曲面形狀。刀具沿著圓柱螺旋線移動過程和與其形狀相同的滾子進行傳動過程是相仿的。銑刀半徑是不能忽略的，加工出的圓柱螺旋槽實際是不同直徑的圓柱上螺旋線的徑向排列，它們的導程相等，螺旋角不等，直徑越大則螺旋角也越大。圖1表示外螺旋線和內螺旋線螺旋升角的比較，N-N’是外螺旋線的法向截面。可以發下，只有外螺旋線與滾子外圓法向截面上相切，而內螺旋線由于其螺旋升角大于外圓螺旋線的，不會與滾子外圓在法向截面相切。這樣螺旋槽的法向截型發生變形，即在N-N’截面上，螺旋槽型面上窄下寬。

這樣，螺旋面的母線與絲桿軸線不相交，螺旋槽側面不是正螺旋面。在絲桿坐標系中，Z軸為絲桿軸線，滾子圓周方向為X軸，XYZ符合右手螺旋法則。螺旋面的準線參數方程為：

因為銑刀與螺旋面外輪廓線相切，切點與絲桿軸線有一定偏移量，該偏移量為r·sin（λ），螺旋升角λ與螺旋線半徑有關。則螺旋面母線參數方程為：

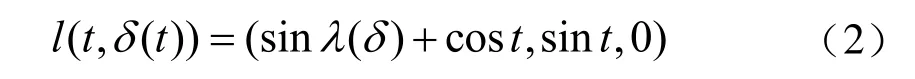
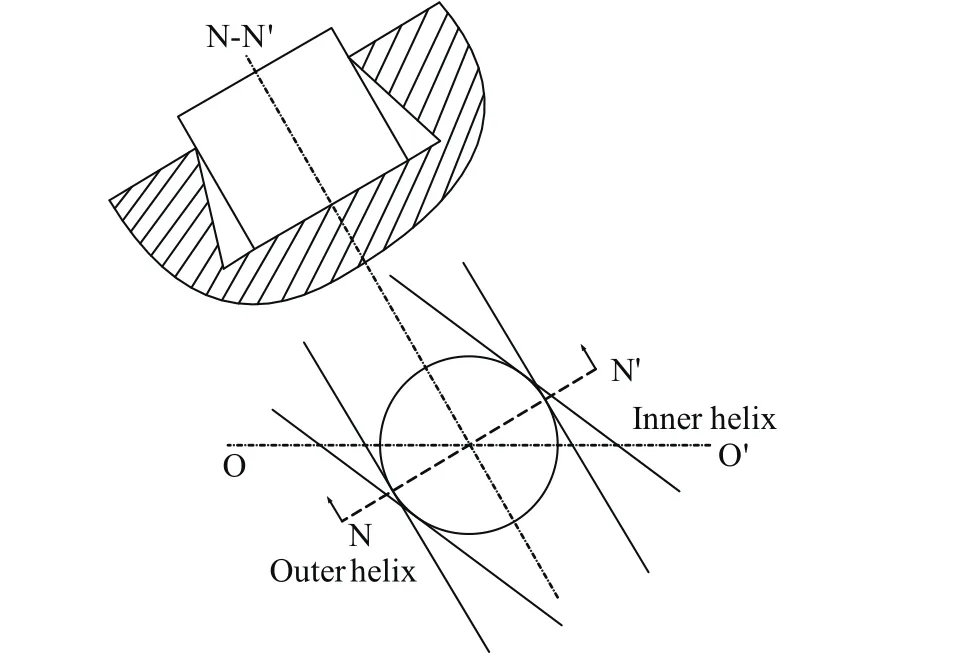
圖1 螺旋槽剖面圖

根據式（1）、式（2）得到螺旋槽側面參數方程為：

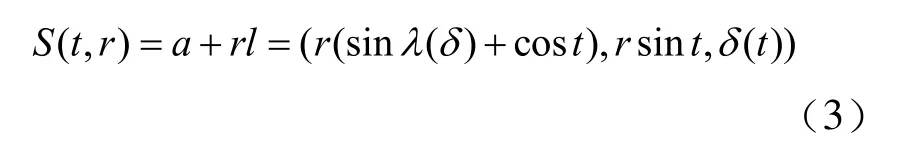
2 變半徑變導程螺旋線數學模型

一般螺旋線的參數方程為：

其中，半徑r和旋轉角度f是軸向位移的函數。

螺旋線的螺旋特性可以由統一的螺旋參數來描述，即螺旋角和導程雖然二者概念不同，但描述螺旋線的同一特性。若考慮螺旋線的旋轉半徑，則表述了圍繞任意旋轉體的變導程螺旋線，螺旋線上任意點P坐標（r，θ，z），螺旋升角λ為z的函數。

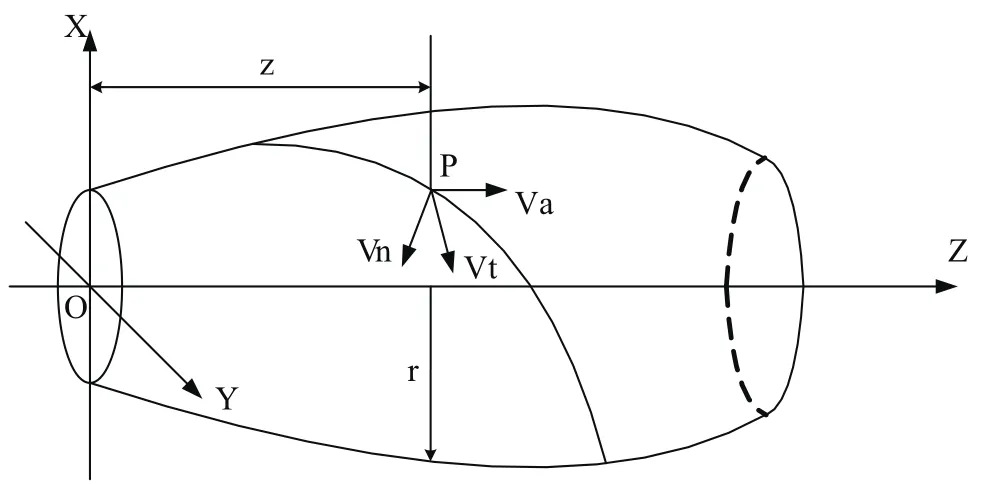
圖2 變半徑變導程螺旋線坐標系

如圖2所示動點P為加工變導程螺旋槽刀具回轉軸與旋轉體母線的交點，其運動速度的三個分量分別為軸向速度VA，周向速度Vt，徑向速度Vg。Vu=VA+ Vg表示沿P點處回轉體母線切線方向速度。其中螺旋升角用速度分量表示為：

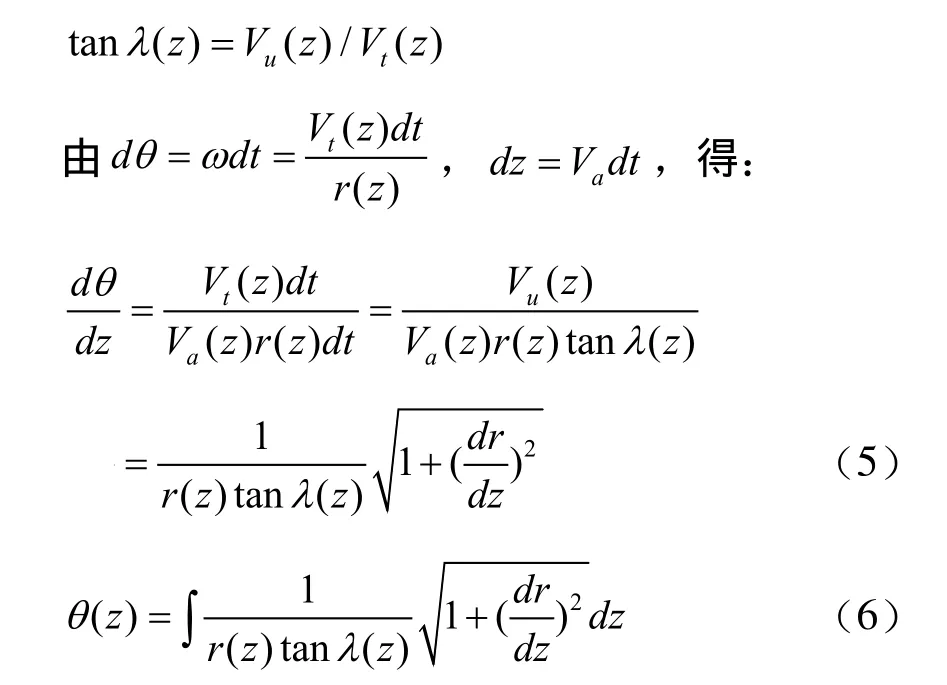
所以旋轉體上螺旋線的局部形狀由θ（z）、λ（z）和 r（z）完全描述。

螺旋線上任意一點坐標為：

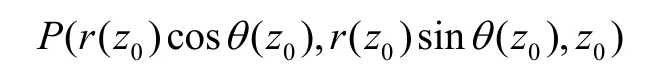
將z用θ表示，則變半徑變導程螺旋線的參數方程為：

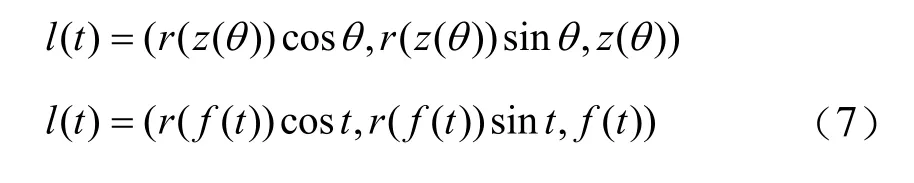
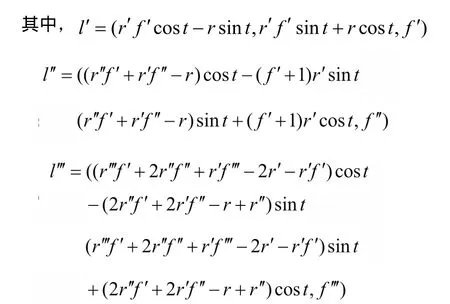
本論文研究對象是變導程螺旋傳動中，滾子傳動軌跡是圓柱螺旋線。當螺旋線的所在旋轉曲面為圓柱面時，r為常數a。則函數f（t）表征了變導程軌跡。

由此，若f = f（t），則：

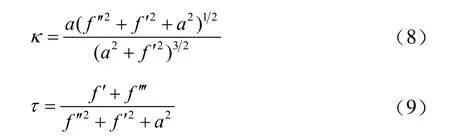
由此可知，給定任意常半徑變導程螺旋線參

數方程l(t)= (ac osθ(t),as inθ(t),f(t))，其任一點

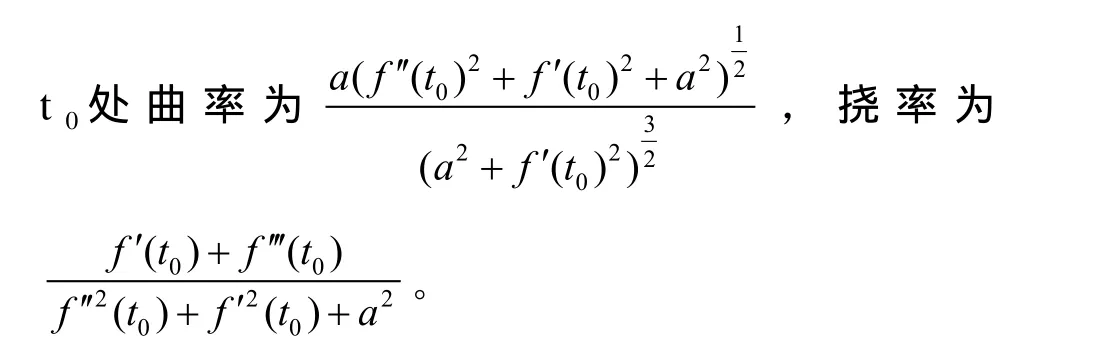
3 圓柱面過度曲線設計

3.1 圓過渡曲線設計

圓柱面上的過渡曲線需要滿足在兩個連接點處至少一階連續，過渡圓能滿足基本的過渡曲線要求，并且本身具有n階連續特征。以下對圓柱面上兩條常導程螺旋線進行圓過渡。

將圓柱面展開，并使曲線G以圓弧過渡連接曲線L1和L2，如圖3所示。

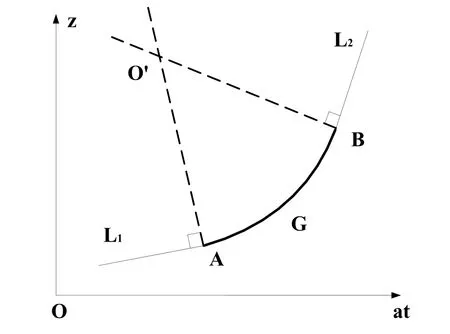
圖3 圓過渡曲線

建立展開圖中局部坐標系，A點坐標為A(atA,zA)，A點斜率為kA=pA/2πa；B點坐標為B(atB,zB)，B點斜率為kB=pB/2πa。易得O'點坐標為：

圓弧的曲率半徑為：

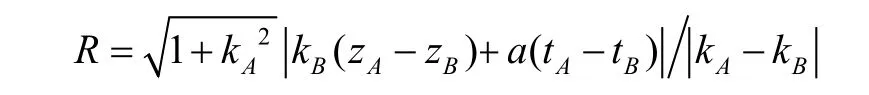
則在全局坐標系下此圓柱面圓弧曲線方程為：

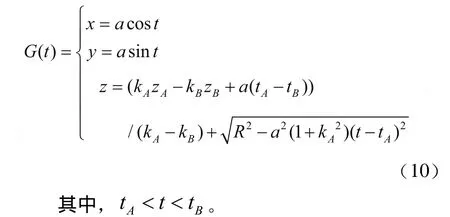
3.2 多項式曲線設計

如圖4中，L1是導程為pA的螺旋線，L2是導程為pB的螺旋線，A為L1的端點，其坐標為(acostA,asintA,zA)；B為L2的端點，其坐標為(acostB,asintB,zB)。要求構造一條連接曲線L1，L2的光滑曲線G，使得曲線G分別與L1和L2在A點和B點相切。

圖4 連接A、B兩點的曲面族示意圖

令曲線G參數方程為：

此時將空間曲線轉化為平面曲線進行研究，得到了連接曲線L1和曲線L2的過渡曲線族G（t，β），β為曲線形狀參數。原螺旋線的坐標轉變成直角坐標Sxoy，這時的參數方程為：

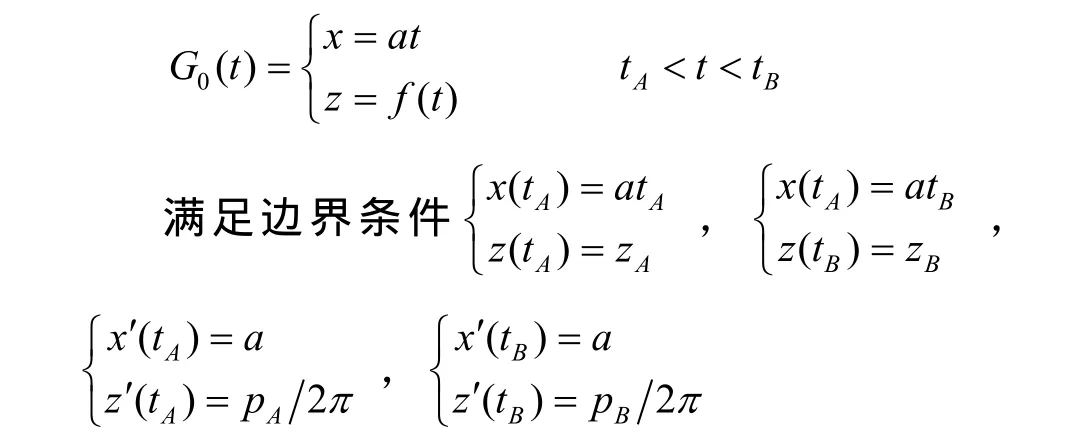
由于需滿足四個邊界條件，將函數z = f（t）定義為四次多項式函數：

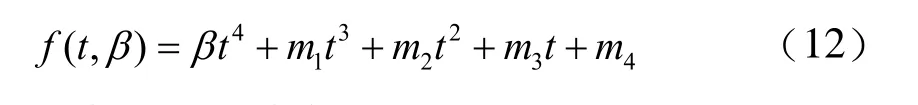
其中，mt為待定系數，β為形狀參數。

將邊界條件分別代入方程（12），得線性方程組：

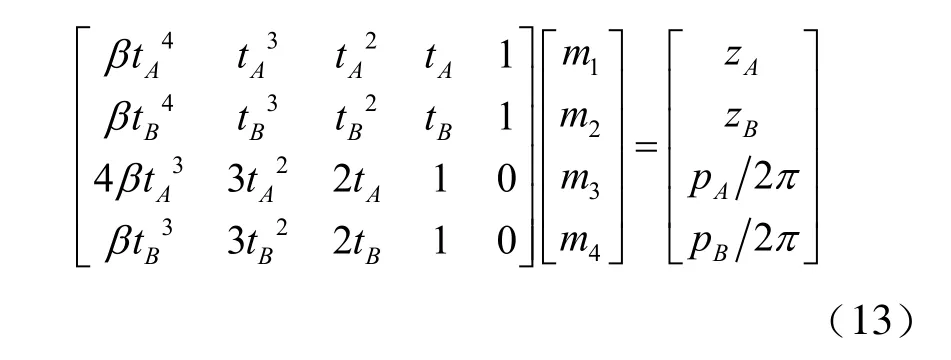
其中β決定了過渡曲線的性質。

[1]Ming J. Tsai；Jan-shiung Sun and Jan-chung Chu.Kinematic design optimization of the variable lead screw mechanism with cone meshing element. Mech. Mach.Theory

[2]J.Y. Liu；H. S. Yan. Surface geometry of variable pitch cylindrical cams with conical meshing elements. ASME Transactions,Jounal of Mechanical Design. 1994,116

[3]S. T. Chiou. Computer integrated design and manufacturing of varialbe pitch lead screw transmission mechanisms.Dynamic designs. 1993,Vol. 31

[4]蕭仲敏. 復雜曲面CAM系統設計的研究[J]. 制造業自動化,2011,33(2).

[5]李和. 汽車曲面品質分析及光順優化方法研究[J]. 制造業自動化,2011,33(2).

Surface modeling and transition helix design for variable lead screw transmission

ZHANG Wei1，SHI Xiang2，LI Dong-bo1

本文對變導程螺旋傳動中螺旋面的通用曲面方程進行建模，建立了螺旋面的變半徑變導程準線方程，并采用圓過渡和多項式曲線過渡兩種方法對螺旋線即準線的過渡部分進行了設計。

變導程；螺旋傳動；過渡螺旋線

張威（1982 -），男，河北唐山人，博士研究生，研究方向為機械電子工程。

TH391

A

1009-0134(2013)01(下)-0132-03

10.3969/j.issn.1009-0134.2013.01(下).38

2012-09-13