基于非線性回歸分析的特高壓直流線路桿塔質量計算

林清海，楊博，陳鵬，任偉

（1.山東電力工程咨詢院有限公司，濟南市 250013；2.國家電網公司運行分公司，北京市 100052）

0 引 言

在輸電線路桿塔優化排位設計中，隨時需要調用桿塔質量（下稱塔重）指標等資料，而準確地計算各種方案的鐵塔質量需花費大量的時間和精力。通常估算鐵塔塔重的方法是在已有施工圖設計塔重的基礎上，只對某種塔型的某種呼高進行塔重估算，而同一型式的不同呼高及荷載條件下的塔重，則采用公式近似估算，但誤差較大。國內外有關塔重估算研究結果發現，塔重與鐵塔呼高和其可能的作用荷載變化值有關。近年來西南電力設計院提出了鐵塔設計荷載與塔重的力矩關系式［1］，并對其影響系數進行了取值分析，其主要優點是對輸電線路鐵塔通過歸納、比較、適配，確立設計荷載與塔重的關系式，為塔重估算方法提供依據。但該關系式存在局限性，如：不適用于特高壓直流線路，關系式中影響塔重的變量過多，操作繁瑣，易出錯。

回歸分析是通過建立數理統計模型來研究變量之間相互關系的一種數理統計方法，對相應的變量進行預測和控制，是進行計量分析的主要工具［2］。Matlab因其面向矩陣的編程特性、出色的圖形處理功能、應用廣泛的模塊集合工具箱以及圖形仿真界面而在研究、解決工程和數學問題中得到廣泛應用［3］。在Matlab中列舉了多種常見的回歸分析函數，可輕松實現對數理統計模型的構建。因此，本文以“±800kV鐵塔典設”［4］的塔型塔重作為數據樣本，用回歸分析的方法，借助Matlab發現桿塔質量與桿塔呼高、荷載條件［5－6］之間的規律性，建立塔重估算數學模型；對不同導地線、氣象區、地形和海拔高度的模塊塔重樣本，按地形和海拔高度進行分類，采用回歸分析的方法，整理歸納出塔重估算關系式，并與實際典設塔重作比較，其誤差小、精度高；在已知地形和海拔高度的條件下，就可以采用桿塔呼高和荷載條件計算塔重，實用有效；本文選取哈鄭線工程中含有多種導線、氣象區、地形和海拔等的設計標段，采用塔重估算關系式計算施工標段總塔重，并與實際塔重作比較，其誤差較小，進一步驗證了關系式的準確性。

1 基本原理及實施方法

1.1 非線性多元回歸分析原理

非線性多元回歸分析的算法［7］如下：

（1）非線性最小二乘法求取參數估計值。該方法以誤差平方和最小為準則來估計非線性靜態模型參數。設y＝f（x，θ），式中θ是參數。這里的非線性是指對參數θ的非線性模型。在估計參數時，模型的關系式f是已知的，經過n次實驗取得樣本數據（x1，y1），（x2，y2），…，（xn，yn）。估計參數（或稱目標函數）選為模型的誤差平方和。

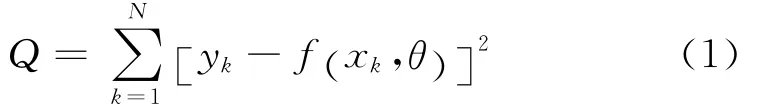
非線性最小二乘法就是求使Q達到極小的參數估計值θ，并采用復雜的優化迭代算法來求解。Matlab中的非線性曲線擬合函數nlinfit和lsqnonlin等使用高斯－牛頓迭代算法可以很好地實現非線性擬合并求解參數估計值和置信區間的功能。

（2）回歸方程的顯著性檢驗。本文采用求取R2可決系數的方法對非線性回歸方程進行顯著性檢驗，具體是：回歸方程中反映因變量n個觀察值與其均值的總離差稱為總平方和（SST）；反映自變量x變化對因變量y取值變化的影響稱為回歸平方和（SSR）；反映除自變量x以外的其他因素對因變量y取值的影響稱為殘差平方和（SSE），三者關系如下式。

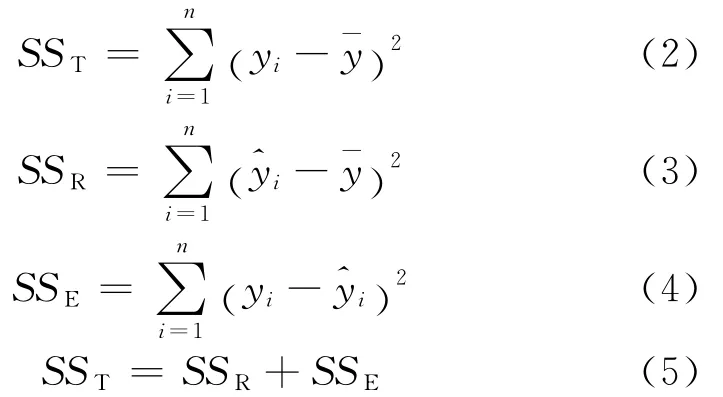
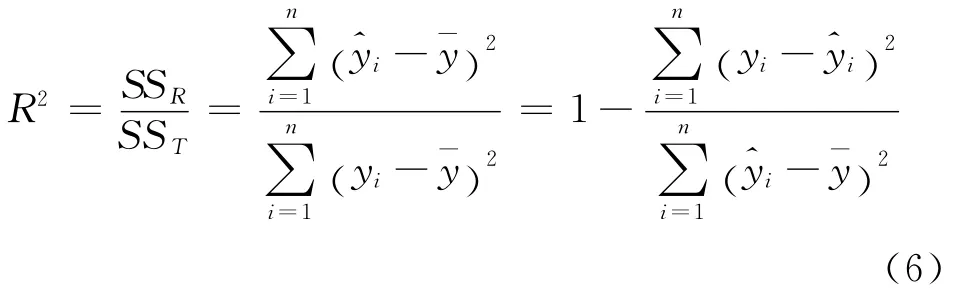
R2可決系數反映了回歸的擬合程度，取值范圍在 ［0，1］之間。若R2→1，說明回歸方程擬合的程度好；若R2→0，說明回歸擬合的程度差。R2的平方根R通常稱為復相關系數，可以看作是因變量y與變量x之間相關關系及密切程度的一種度量。

1.2 塔重估算非線性多元回歸分析的算法

桿塔的塔重可用下式表示［1］：

式中：W 為塔重指標；H為桿塔呼高；fh為水平荷載；fv為垂直荷載；ft為縱向荷載（直線塔時此值為0）。從上式的函數可確定任何一個參數變化對塔重的影響。

本文以“±800kV鐵塔典設”的塔型塔重作為數據樣本，用回歸分析的方法，借助Matlab發現桿塔質量與桿塔呼高、荷載條件之間的規律性，建立塔重估算數學模型。塔重估算回歸分析的算法如圖1所示。

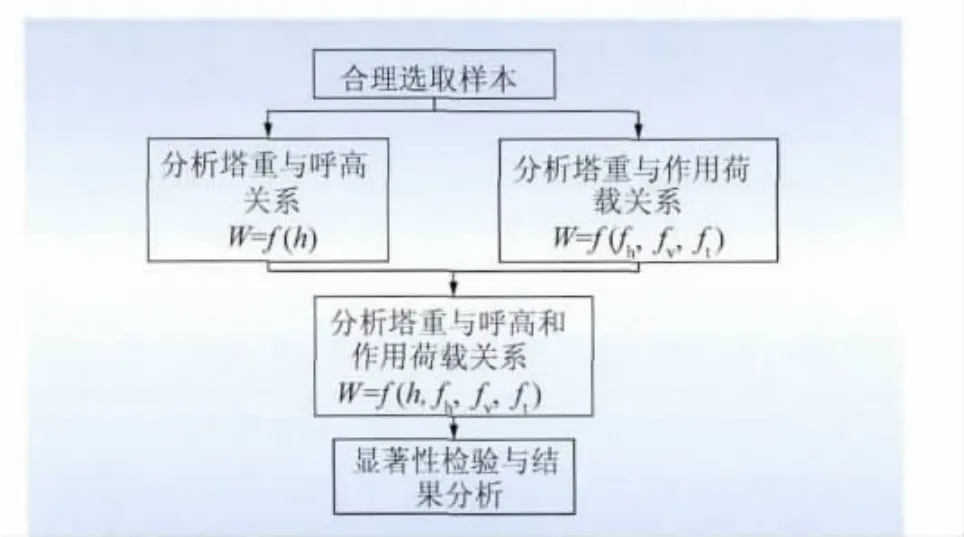
圖1 算法流程Fig.1 Algorithm flow

2 算例分析

2.1 數據樣本的選取

首先以“±800kV鐵塔典設”中通用設計模塊8B2為樣本進行算例分析，按照不同地形和海拔高度，對不同導地線、氣象區的典設塔重樣本，采用回歸分析的方法進行分類歸納，借助Matlab發現桿塔質量與桿塔呼高、荷載條件之間的規律性，建立塔重估算數學模型，并對其進行準確性校驗。

模塊8B2主要技術條件：導線型號為6×JL／G3A－1000／45；地線型號為JLB20A－150；設計風速為33m／s；覆冰厚度為10mm；地形為平丘；海拔高度≤2300m。

模塊8B2塔為干字型平丘塔，按平腿設計，直線塔懸垂串采用V型串，耐張塔跳線采用雙V型鼠籠式硬跳；直線塔采用5塔方案，另加I型防串倒塔、II型跨越塔和II型直線轉角塔，耐張塔采用4塔方案，即20°分檔，4型塔取60°90°為1檔。

2.2 桿塔質量與呼高的關系

桿塔塔重計算系統荷載等條件不變時，桿塔呼高越高則塔重也越大。為確定桿塔質量W與桿塔呼高h的關系式W＝f（h），首先運用Matlab對已知施工圖塔重、桿塔呼高數據作散點圖觀察數據規律，然后確定其回歸指數曲線模型，如圖2所示。

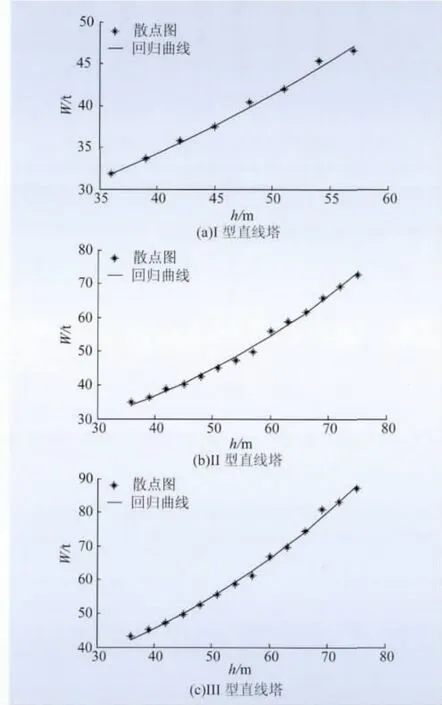
圖2 直線塔質量與呼高的關系散點圖及回歸曲線Fig.2 Scatter diagram and regression curve of relationship between supporting tower weight and height

圖2表示了直線塔3種塔型的桿塔質量與呼高的指數關系。使用式（8）描述的指數關系來擬合塔重時，誤差很小，其平均誤差為0～2.4%，直線塔質量與呼高的關系用回歸模型關系式表示。表1中給出了對該模型關系式的檢驗：在參數估計值95%置信區間下，可決系數R2為0.983，非常接近1，因此，使用該模型關系式進行擬合是合理的。

表1 直線塔質量與呼高回歸關系式Tab.1 Regression relationship between supporting tower weight and height

表中：a、b為常數，對于不同塔型，a值不同，而b值基本一致。b值的范圍為0.0147～0.0192，桿塔級間（1 m1級）比值為e0.0147×1＝1.015～e0.0192×1＝1.019，所以b值可采用加權平均法取一定值，此處b的平均值為0.0173，級間比值為1.017。

2.3 桿塔質量與荷載的關系

桿塔呼高條件不變時，直線塔設計水平荷載和垂直荷載越大則桿塔質量也越大。為了便于分析桿塔質量與荷載條件的關系，可選擇一個桿塔呼高作為研究對象，這個呼高稱為標準塔高。標準塔高取57 m時，不同塔型的塔重、各極導地線水平荷載（最大風工況）、垂直荷載（覆冰工況）之和如表2所示。

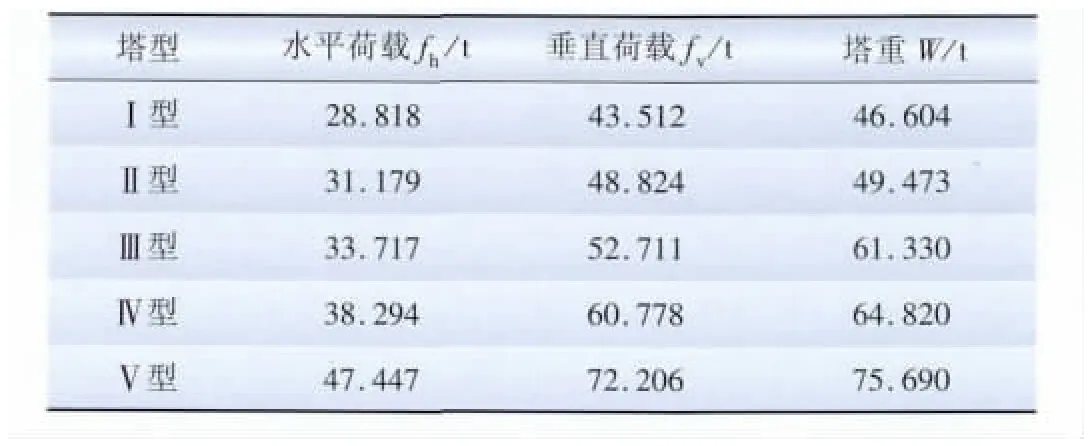
表2 直線塔質量與桿塔荷載關系表Tab.2 Supporting tower weight and load

為了得到桿塔質量和荷載的關系式，對表2中的W、fh、fv進行多元回歸分析，運用Matlab分別作 W～fh，W～fv關系散點圖及回歸曲線，如圖3所示，發現數據分布符合線性規律，從而確定其回歸模型。

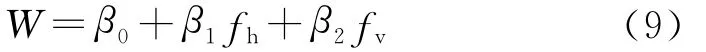
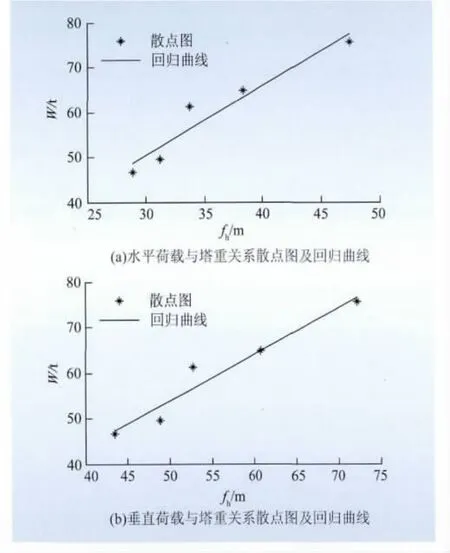
圖3 直線塔質量（W）與荷載（fh，fv）的關系散點圖及回歸曲線Fig.3 Scatter diagram and regression curve of relationship between supporting tower weight（W）and load fh，fv

圖3所示直線塔質量與荷載的關系，采用回歸模型關系式可以表示為

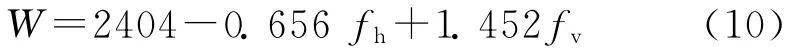
使用式（10）描述的線性關系來擬合塔重時，誤差很小，其擬合的平均誤差為0.0%～7.7%，對該模型進行顯著性檢驗，在參數估計值95%置信區間下，可決系數R2為0.951，非常接近1，因此使用該模型關系式進行擬合是合理的。

2.4 桿塔質量與呼高及荷載的關系

式（8）為直線塔荷載條件一定時桿塔質量與呼高的指數關系式，式（9）為標準塔高時桿塔質量與荷載條件的線性關系式，綜合上述2式即得到桿塔質量與呼高、荷載條件的關系式

由于地形與塔腿設計有關，海拔高度與極間距離、懸垂V串間隙等控制塔頭尺寸的因素有關，雖然以上兩者在塔重中所占比例很小，但考慮到塔重估算的準確性，仍不宜忽略。因此本文按地形（平丘、山地）和海拔高度進行分類，選取“±800kV鐵塔典設”中不同導地線（導線截面900mm2的8A模塊、1000mm2的8B模塊）、氣象區、地形和海拔高度（≤2300m）等的非特殊塔型作為塔重樣本；采用非線性多元回歸分析的方法，整理并歸納出塔重估算關系式見表3。

表3 直線塔估重關系式樣例Tab.3 Sample of estimation formula for supporting tower weight

利用表3塔重估算樣例關系式可以在已知海拔高度和地形的情況下，通過桿塔呼高和荷載條件預測桿塔的重量。圖4給出了采用估算關系式計算模塊8B2直線塔的塔重結果與實際典設塔重的對比情況，由圖4可見絕對誤差在5%以內，且大部分誤差在3%以內。

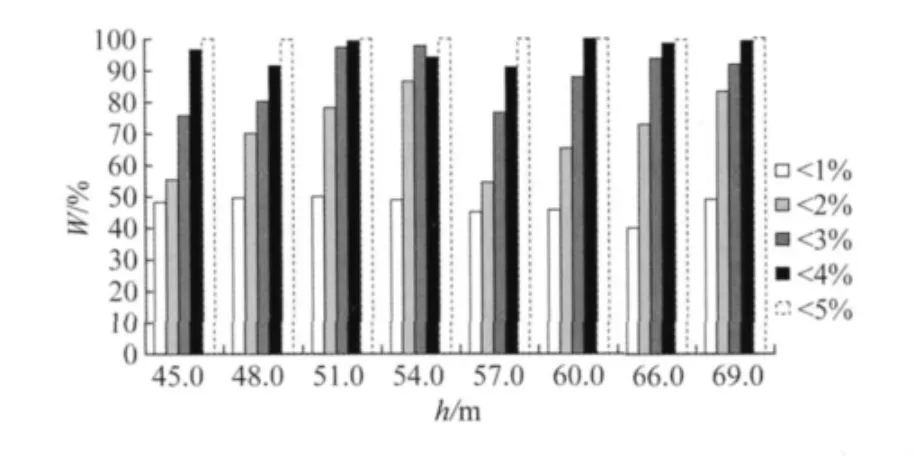
圖4 直線塔各呼高估算塔重與實際塔重比較Fig.4 Comparison of supporting tower weight between estimation values based on different height and actual values

2.5 轉角塔桿塔質量估算方法

由于轉角塔的角度力一方面會導致水平荷載fh增加，另一方面會產生垂直于鐵塔橫擔方向的縱向荷載ft，因此轉角塔塔重受其轉角角度影響很大［8－10］，其塔重估算數學模型關系式為

本文繼續以“±800kV鐵塔典設”的非特殊塔型作為塔重樣本，采用非線性多元回歸分析法，整理并歸納出塔重估算關系見表4。

表4 轉角塔估重關系式樣例Tab.4 Sample of estimation formula for angle tower weight

利用表4的塔重估算樣例關系式可以在已知海拔高度（≤2300 m）和地形的情況下，通過桿塔呼高和荷載條件預測桿塔的重量，圖5給出了采用估算關系式計算模塊8B2轉角塔的塔重結果與實際典設塔重的對比情況，由圖5可見絕對誤差在6%以內，且大部分誤差在3%以內。

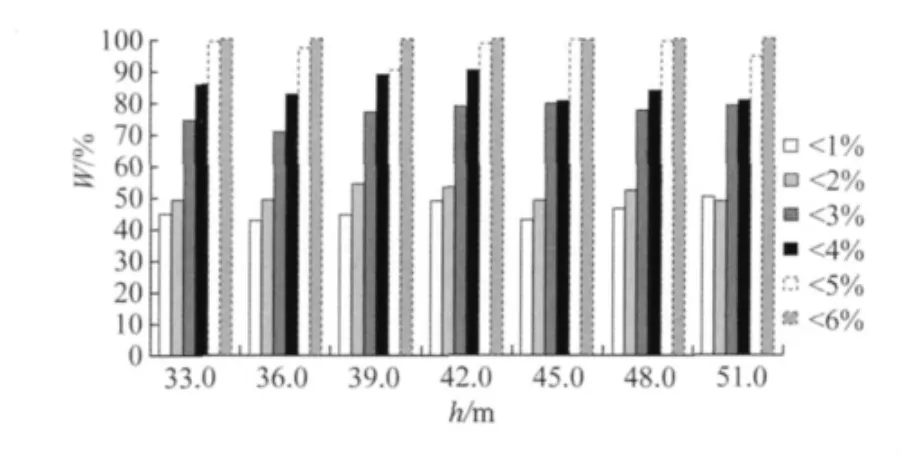
圖5 轉角塔各呼高估算塔重與施工圖塔重比較Fig.5 Comparison of angle tower weight between estimation values based on different height and values in construction drawing

3 工程實例驗證

為繼續驗證該塔重估算關系式，特選取哈鄭線工程包7設計標段，其線路長度91.2km，設計條件如表5所示。

表5 哈鄭線工程包7標段設計條件Tab.5 7th bid segment design condition of Hazheng transmission line project

計算不同導線型式的荷載，采用分類歸納的塔重估算關系式計算標段總塔重，并與施工圖設計塔重作比較，如圖6所示。直線塔總塔重誤差小于3.3%；轉角塔總塔重誤差小于6.4%；標段總塔重誤差小于4.5%，該誤差對于設計方案比選及優化是可以接受的。

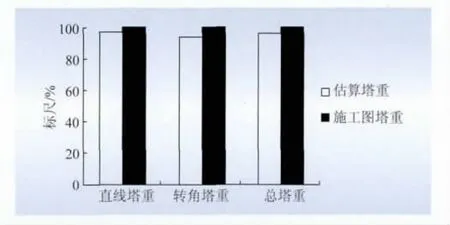
圖6 設計標段估算塔重與施工圖塔重比較Fig.6 Comparison of tower weight between estimation values in design segment and values in construction drawing

4 結 語

以“±800kV鐵塔典設”的塔型塔重作為數據樣本，用回歸分析的方法，借助Matlab發現桿塔質量與桿塔呼高、荷載條件之間的規律性，建立了塔重估算數學模型關系式。

為便于使用，對不同導地線、氣象區、地形和海拔高度的模塊塔重樣本，按地形和海拔高度進行分類，采用非線性多元回歸分析的方法，整理并歸納出塔重估算關系式。因此，在已知地形和海拔高度的條件下，即可以使用桿塔呼高和荷載條件估算塔重。

估算塔重結果分別與實際典設塔重，實際哈鄭線設計標段總塔重作比較，其誤差小，精度高，因此該塔重估算的方法及關系式可用于設計方案的比選及優化。

［1］肖洪偉，肖兵，李力，等.輸電線路鐵塔設計荷載與塔重的關系式分析［J］.電力建設，2006，27（9）：4－6.

［2］龍永紅.概率論與數理統計［M］.北京：高等教育出版社，2004：215－267.

［3］張德豐.MATLAB概率與數理統計分析［M］.北京：機械工業出版社，2010：233－260.

［4］劉振亞等.國家電網公司輸變電工程±800kV特高壓直流輸電線路鐵塔分冊［M］.北京：中國電力出版社，2012.

［5］于剛，梁政平，李勇偉，等.±800kV直流架空輸電線路設計規范（報批稿）［M］.北京：中國電力出版社，2012：18－24.

［6］張殿生，倪宗德，張洞明，等.電力工程高壓送電線路設計手冊［M］.北京：中國電力出版社，1999：166－206.

［7］Madsen K，Nielsen H B，Tingleff O，et al.Methods for non－linear least squares problems［R］.Denmark：Technical University of Denmark，2004.

［8］唐家德.基于MATLAB的非線性曲線擬合［J］.計算機與現代化，2008，154（6）：15－19.

［9］John H Mathews，Kurtis D Fink.數值方法：MATLAB版［M］.北京：電子工業出版社，2005：195－215.

［10］徐萃薇，孫繩武.計算方法引論［M］.北京：高等教育出版社，2002：62－85.