用小波矩陣形式改進Daubechieschies小波的正交性
張旭俊
(江西省電力科學研究院,江西南昌 330096)
0 引言
小波理論是20世紀的數學里程碑,Haar小波簡單對稱,但它不連續、不可微的缺點,數學家不能接受。尋找具有緊支撐、連續、可微的小波十分困難,法國著名數學家Meyer曾企圖證明小波正交基(Haar小波除外)并不存在,但最后他提出多分辨小波分析方法,并由數學家Daubechies提出一個正交的小波族,當N=1時它就是Haar小波,N≥2時,就是Daubechies小波族,但兩者關于小波正交的理念是完全不同的。經典小波理論是在傅里葉變換的廣義積分中表達小波基正交條件的,大篇理論敘述中,遲遲不見小波在時域中的形象,讀者理解較難,特別是對離散的等距采樣數據的小波分析而言,由于數據長度有限,會發生邊緣數據小波分析的失真。本文將用小波矩陣的方法銓明并改造Daubechies小波矩陣的正交性,用小波矩陣分析是從時域中來理解正交性的,不涉及傅里葉廣義積分的概念,讀者理解要容易得多,從小矩陣導入方法,讀者不難用舉一反三的推理,擴展到任意階的大矩陣。
1 用Haar小波矩陣作光滑分解
作者用Haar小波矩陣來分析等距采樣數據,為了分析結果的平滑,先依不同尺度進行平均值濾波、數據壓縮,再光滑插值重構主體成分的“恢復像”,將“原始信號”減去主體成分的“恢復像”,就得到按時域分布的細節:“總諧波像”,它也是光滑的曲線。這樣就基本上解決了對系列數據按“時-頻”分析的問題。

由原始采樣數據 求出小波系數C如下:

由小波系數C重構原始函數F如下:

以下只以實例說明Haar矩陣按雙尺度分解的過程和結果。
設采樣數據由式(4)得到f(i),稱之為F列向量,采樣點數取N=2n=128點,相應的Haar矩陣B是128階方陣,
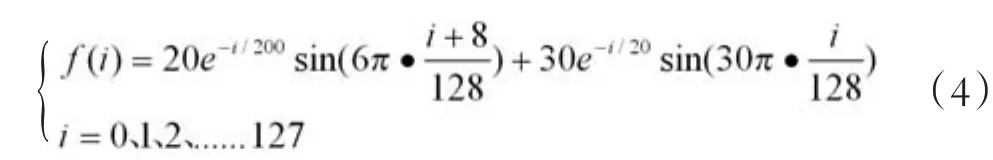
若尺度壓縮選擇取2m=8倍,即略去m=3層以上的高次小波,于是只需保留B矩陣的上面2n-m=16行的數據,稱作BU矩陣,它是16×128階矩陣,函數重構解出的f1(i)步驟很簡單,它無需寫出128階B矩陣作運算,其f1(i)的結果就是從開始,每連續8個點都用它們相應的平均值代替,由此所形成階梯波的“模糊像”如圖1。再將每連續8個相同的數據只保留一個(圖1下的小圓圈),得到壓縮數據s[k],其中k=0、1、2、…….15,如式(5)
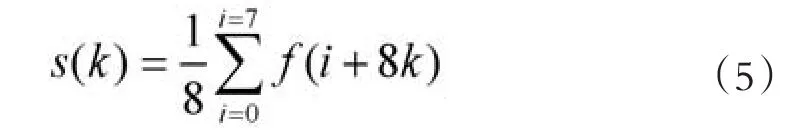

圖1 Haar小波矩陣分析的效果
再采用光滑插值的方法,在 和 中間求雙拋物線的平均值,從而將這16點壓縮數據擴展成128點,就得到主體成分的“恢復像”,再將“原始像”減去“恢復像”得到“總諧波像”,它也是光滑曲線,如圖1。這樣就得到的“時-頻”分解結果。
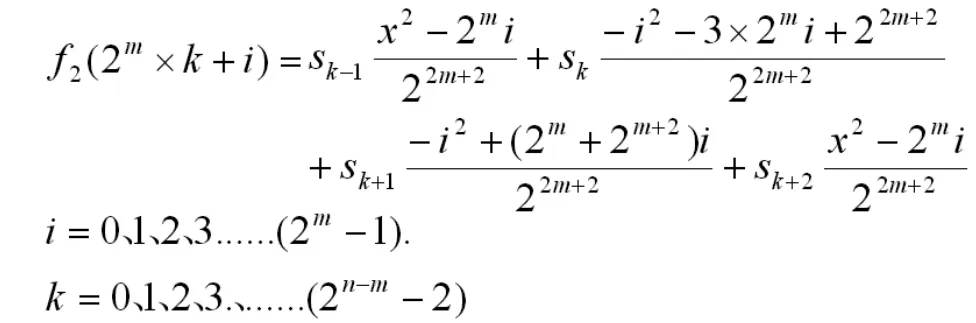
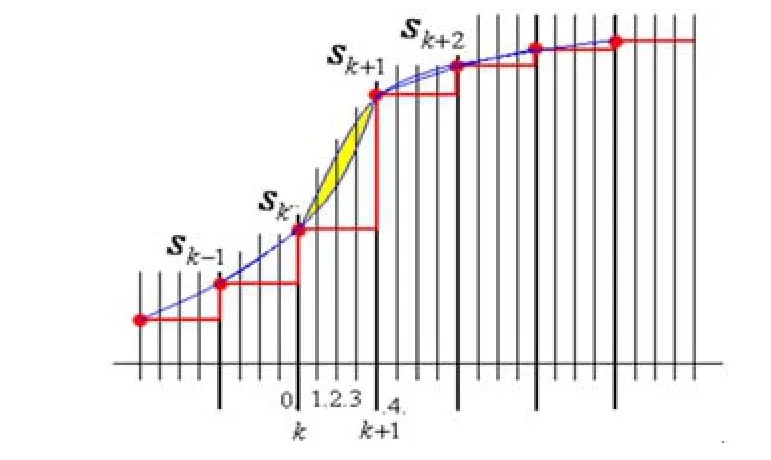
圖2 用雙拋物線法求平均插值
2 正交子波變換
多尺度表達的離散小波函數

經典小波重構的公式是:

引入雙尺度函數和小波函數,及其傅里葉變換函數,如公式(9)、(10),
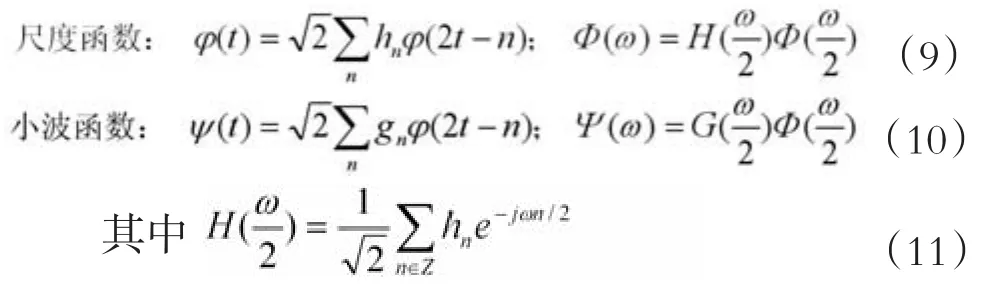
尺度函數和另一平移后的尺度函數應當是正交的,用公式表示如下,

同理也可得到關于小波正交條件的公式(13)

由小波函數和尺度函數的正交關系可有:

3 Daubechies小波族
法國數學家Daubechies提出了一組正交小波的濾波函數 的公式(15):
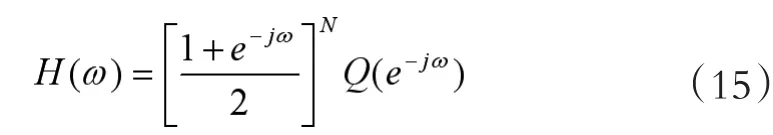
其中 是有關 的(N-1)次多項式。

顯然它滿足尺度函數的正交條件(12)式。
2)當N=2時Daubechies小波的尺度濾波函數直接寫出為:
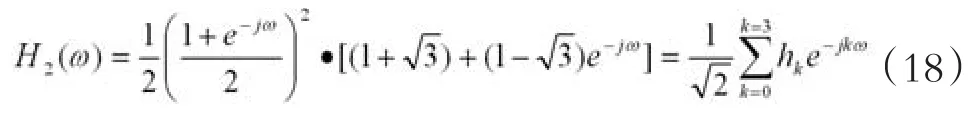
展開后可得其中4個系數是:

相應的4個小波系數為:

一般也簡稱其為Db4小波,參考資料中對各種N下的Daubechies小波,都具有2N個尺度系數,簡稱Db(2N).為驗證其正交性,改寫(18)如下:
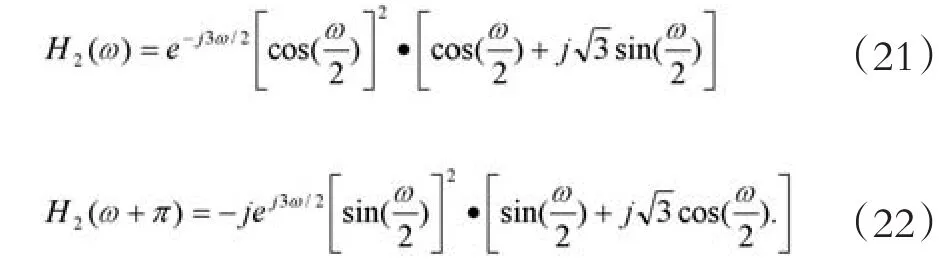
可得:

這種在頻域中驗證尺度函數的正交性,很難使讀者對小波分解有感性認識,而且也見不到小波的形狀。
4 Db4小波矩陣
特以N=2時的Daubechies小波為例,簡稱Db4小波。我們感興趣的依然是希望能像Haar小波矩陣那樣展開,一次性地把各個層次的小波都計算出來,但這是不可能做到的,這就是數學家Meyer曾企圖證明小波正交基(Haar小波除外)并不存在。但最后他提出多分辨小波分析方法,就是按尺度和小波系數,一層一層地剝開,逐次顯示該層次的小波和尺度的幅值,每剝一層信號點數就應當減半。為描述這個思路還是用8階矩陣來加以說明。前4行放置尺度波形,后4行放置小波波形,如第1行是4個尺度系數,右邊4個零,第5行是4個小波系數,右邊4個零。第2、6行是將第1、5行向右移位2列,第3、7行是將第2、6行向右移位2列,第4、8行是將第3、7行向右移位2列,這時出現了截斷的現象,有兩個列跑出了方矩陣的范圍。方矩陣的右邊是列向量F,它是原始信號的數據等號右邊的列向量X是待求的尺度幅值c和小波幅值d。從幾何意義看,尺度波形就是小波波形就是,解這個聯立方程就可將原始信號分解為尺度和小波的幅值,

把(24)式簡寫成(25)式,如果希望按原來尺度和小波的波形重構原函數,就應當如公式(26)那樣,但關鍵是H矩陣是否是正交矩陣,驗證如下:

如(27)式所示,H不是正交矩陣,需加以改造,

如果把第4、8行移位時截斷的兩個列,循環地移到相應行中的第1、2列上,可有(28)式,從物理意義上理解佗相當于原始數據是周期性循環的。

簡寫為B·F=X……(29),令人興奮的是B矩陣是正交矩陣,
從而可有波形重構公式(32)


下面以前例128點的采樣數據進行Db4矩陣的分解重構工作,先后進行3層剝離,如圖3所示。為了對比在圖的右邊畫出用Haar矩陣作光滑分解的對應結果,相當于壓縮2、4、8倍,由于Haar矩陣光滑分解采用插值處理,各層的“恢復像”都有128點數據畫線,比較光滑,可見用Haar矩陣作光滑分解依然具有使用方便的優勢,且它能直接進入某個尺度進行分解。
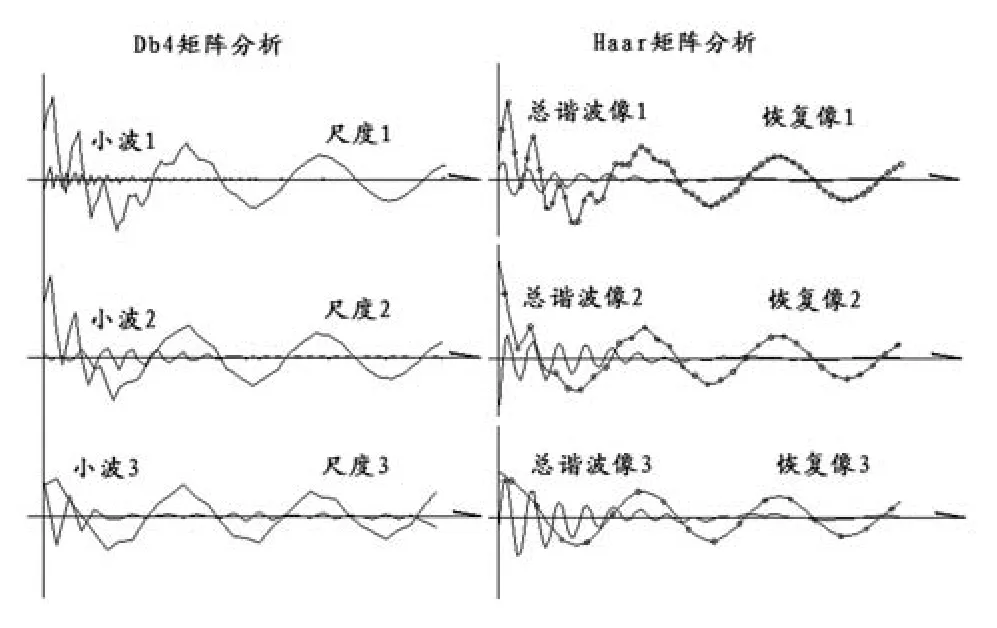
圖3 兩種小波矩陣分析法結果的對比
5 結論
必須注意Haar矩陣的正交性可以一次性將原始采樣點數據分解為:直流、2次、4次、8次……到2n-1次小波,而DB4矩陣的正交性卻只能將N=2n點數據分解為:尺度和2n-1次小波,其中尺度就是所有2n-m次小波的總和,(m=2、3、……n),DB4分解雖然不能一次到位,卻能接連進行分解。法國著名數學家Meyer曾企圖證明小波正交基(Haar小波除外)并不存在,然后他又提出雙尺度多分辨小波的分析方法,創造出多層剝離的另一種的正交概念,這也是卓越的創舉,本文用小波矩陣的方法把這兩者之間的差異明白地表達出來。令人興奮的是,在離散函數的分析時,Daubechies小波DB4、DB6、…….DB20等都可以按本文的方法構成正交的B矩陣,從而使小波分析的概念完全轉到時域中來理解。
如第一節所述,Harr小波矩陣的基小波支撐區是[1,2],沒有前后的拖尾,像切香腸一樣清晰,它的正交性明確。至于其不連續、不可微的缺點,可通過平均值濾波,數據壓縮,光滑插值膨脹,完全得到解決。所以作者特推薦用Harr小波矩陣作光滑分解的方法。
[1]張旭俊.用小波矩陣作小波分析[J].電力系統自動化,1999(24).
[2]張旭俊.小波分解和高次小波差分的奇異點[J].電力自動化設備,2001(2).
[3]張旭俊.用小波矩陣分析法進行函數的分解與重構[J].江西電力,2007(4).
[4]張旭俊.用小波矩陣分析Mallat算法的物理幾何含義[J].江西電力,2010(1).
[5]趙松年.子波變換與子波分析[M].北京:電子工業出版社,1996.
[6]程正興著.小波分析算法與應用,[M].西安西安交通大學出版社,1998.

