一種雙邊核函數(shù)的新Harris角點檢測算法

朱麗娟

（湖北文理學院，湖北 襄陽441053）

一種雙邊核函數(shù)的新Harris角點檢測算法

朱麗娟

（湖北文理學院，湖北 襄陽441053）

針對目前Harris算法存在的對噪聲敏感和檢測率不高的不足，提出一種雙邊核函數(shù)的新Harris角點檢測算法。算法首先采用雙邊濾波器來代替原有的高斯低通濾波器，來增強算法的魯棒性；接著采用多尺度分解來建立真實角點和偽角點的分割閾值。實驗結果表明，提出的算法能精確地檢測圖像角點。

Harris算法；雙邊濾波；角點檢測

1 引 言

角點是一種重要的圖像局部特征點，已被廣泛應用于立體匹配、圖像配準、全景拼接、目標檢測與跟蹤、電子穩(wěn)像、相機標定等技術中［1-3］。角點檢測算法大體可以分為邊緣輪廓法，模板匹配法和灰度信息法三類［1-2］。邊緣輪廓法主要通過在圖像邊緣上進行特征分析來定義和提取角點，算法嚴重依賴于邊緣線的提取，存在著復雜度高，計算量大，易檢測失敗的缺點；模板匹配法通過定義角點模板和圖像區(qū)域搜索匹配來檢測角點，由于角點模板的設計依賴于人為經(jīng)驗，同樣存在著模型復雜，計算代價高的缺陷；而灰度信息法主要通過計算點的曲率及梯度來檢測角點，克服了前兩類算法的缺陷，在實際中得到了廣泛的應用。

目前典型的灰度角點檢測算法主要有Moravec算法［4］、Harris算法［5］、SUSAN算法［6］等，其中，Harris算法在Moravec算法對興趣點的描述基礎上，利用灰度函數(shù)的自相關矩陣來實現(xiàn)角點的檢測，是目前效果較好的角點檢測算法；然而在實際應用中，Harris算法存在著對噪聲敏感，角點信息丟失，定位精度不高等不足。針對這些不足，文獻［7］提出采用拉普拉斯（Laplace）算子來提取角點的尺度，建立了尺度不變的Laplace改進算法和仿射不變的仿射改進算法；文獻［8］提出了光照改變條件下的Harris魯棒性改進算法，文獻［9］提出了基于概率密度的角點均勻性改進算法，文獻［10］提出了應用于復雜紋理圖像的自適應分數(shù)階微分改進算法等。這些算法雖然對幾何不變形和光照不變性進行了改進，然而仍然存在對噪聲敏感、定位精度不高的缺陷。針對這些缺陷，本文提出一種雙邊核函數(shù)的新Harris角點檢測算法，仿真實驗表明，提出的算法具有抑制噪聲角點、檢測率和定位精度較高的優(yōu)點。

2 Harris角點檢測算法

Harris角點檢測算法［5］利用Taylor級數(shù)展開，計算窗口像素（x，y）T在鄰域W內移動的灰度變化量為：

其中，矩陣M描述了圖像在點（x，y）的局部灰度結構信息，用公式表示為：

式中，Ix和Iy分別為圖像一階灰度梯度；wi，j是以（x，y）為 中 心 的 高 斯 核 函 數(shù) wi，j=

如果矩陣M的兩個特征值都比較大，說明在該點的圖像灰度自相關函數(shù)E（x，y）的兩個正交方向上的極值曲率均較大，認為該點是角點，Harris角點響應函數(shù)（CRF）為：

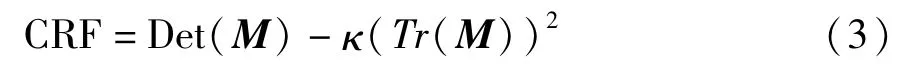
其中，Det為矩陣的行列式；Tr為矩陣的跡；κ為經(jīng)驗參數(shù)值。

在實際運用中發(fā)現(xiàn)，用高斯核函數(shù)作為平滑濾波器由于圖像過度平滑而導致一些較弱的角點被過濾，造成正確角點的漏檢和定位精度的降低，針對這個問題，提出如下改進算法：平滑濾波器不用高斯濾波器，而選用雙邊濾波器。

3 一種雙邊核函數(shù)的新Harris角點檢測算法

3.1 集成灰度距離的雙邊核函數(shù)

由于原始Harris算法存在對噪聲敏感而漏檢正確角點，因此采用雙邊濾波［11］對空域高斯低通濾波進行改進。雙邊濾波的特點是對圖像的每一點像素采用其空間相鄰距離以及灰度相近距離的像素值的加權平均值代替原來的值，其輸出圖像在保護圖像結構信息的同時抑制了噪聲。

利用這兩個距離建立新的雙邊濾波核函數(shù)為：

其中，σs為空間距離標準差；σg為灰度距離標準差；C為歸一化常數(shù)，表示為：

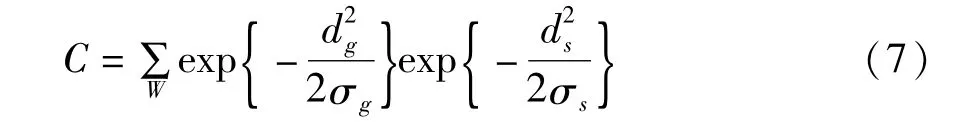
利用核函數(shù)，得到新的局部自相關函數(shù)為：

3.2 基于尺度空間的角點檢測算法

為了解決原始Harris算法在單尺度下由于定位精確度不夠、角點位置偏移而提取出的偽角點問題，采用文獻［7］的尺度空間改進技術，采用高斯核對圖像進行多尺度分解，得到多尺度的自相關函數(shù)為：

式中，w′是w′i，j的縮寫，而分別是和的縮寫；G（σi）為高斯核；?為卷積；σi為積分尺度；σd為微分尺度，詳細信息參考文獻［7］。

將帶有尺度Mσd，σi代入公式（3），得到新的具有尺度響應函數(shù)為：

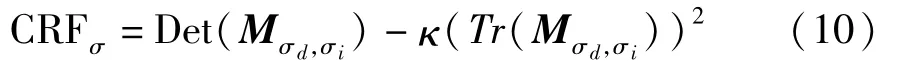
令R0為圖像在尺度為零時候選角點的數(shù)目，Rξ（l）為尺度為L時候選角點的數(shù)目，經(jīng)過研究發(fā)現(xiàn)，真實角點特征隨著尺度的增長變化緩慢，而偽角點特征快速下降，因此建立閾值選取公式為：

其中，T為選擇的閾值。

這樣使用式（10）、式（11）能夠去除大量的偽角點，提高角點檢測的性能。

4 實驗結果和討論

為了測試提出算法的角點檢測性能，在Windows XP操作系統(tǒng)下，采用MATLAB編程軟件，選用標準測試圖像和自然圖像House分別進行仿真實驗，算法中的具體參數(shù)設置為：尺度L=3，經(jīng)驗參數(shù)κ=0.02，角點閾值T=1.00。

首先利用本文算法和文獻［5］、［6］、［12］的算法對角點特征明顯的標準測試圖像blocks進行實驗，窗口大小為21×21，得到的角點檢測效果如圖1所示，具體的實驗結果指標如表1所示。

圖1 blocks圖像實驗結果

表1 blocks圖像實驗結果

分析表1數(shù)據(jù)，可以看出經(jīng)典Harris算法（文獻［5］）的各項檢測性能均優(yōu)于SUSAN算法（文獻［6］），但是丟失了部分角點信息（如圖1（b）所示），漏檢率高于文獻［12］。而本文提出的算法的檢測率和漏檢率均為最好，沒有產(chǎn)生偽角點。

接著對角點特征不是很明顯的自然圖像House進行實驗，窗口大小為13×13，得到的角點檢測效果如圖2所示，具體的實驗結果指標如表2所示。

圖2 House圖像實驗結果

表2 House圖像實驗結果

從表2中數(shù)據(jù)可以看出Harris算法導致許多角點信息被遺漏，并且產(chǎn)生了大量的偽角點，而本文提出的算法更精確地檢測到了正確角點，同時偽角點的數(shù)量也大幅減少。

分析以上兩個實驗，可以看出本文提出算法的角點定位比較準確并且能檢測到更多的角點，得到了比Harris算法更好的檢測結果。

5 結 論

提出了一種新Harris角點檢測算法，算法通過用雙邊核函數(shù)和多尺度圖像分解來解決原有Harris算法的角點信息丟失，定位精度不高的不足，在blocks和House圖像上的仿真實驗表明新算法角點定位比較準確且能檢測到更多的角點，得到比已有算法更好的檢測結果。算法的不足之處為計算時間稍長，這將是作者下一步的努力方向。

［1］ Mokhtarian F，Mohanna F.Performance evaluation of corner detectors using consistency and accuracy measures［J］.Computer Vision and Image Understanding，2006，102：81-94.

［2］ Aan?s S H，Dahl A，Pedersen K S.Interesting interest points［J］.International Journal of Computer Vision，2012，97（1）：18-35.

［3］ Zhou Yajun，Tao Shengxiang，Zhang Shu，et al.Image stabilization algorithm based on Harris［J］.Laser&Infrared，2009，39（5）：555-557.（in Chinese）

周亞軍，陶聲祥，張舒，等.一種基于Harris角點特征的穩(wěn)像算法［J］.激光與紅外，2009，39（5）：555-557.

［4］ Moravec H P.Towards automatic visual obstacle avoidance［C］//Proc of International Joint Conference on Artificial Intelligence，1977：584-590.

［5］ Harris C，Stephens M.A combined corner and edge detector［C］//Proc of the 4thAlvey Vision Conference，1988：147-151.

［6］ Smith SM，Brady I，M Susan.A new approach to low-level image processing［J］.International Journal of Computer Vision，1997，23（1）：45-78.

［7］ Mikolajczyk K，Schmid C.Scale&affine invariant interestpoint detectors［J］.International Journal of Computer Vision，2004，60（1）：63-86.

［8］ GevrekciM，Gunturk B K.Reliable interest point detection under large illumination variations［C］//Proc of IEEE International Conference on Image Processing，2008：869-872.

［9］ Sun Da，Tang Xianglong，Liu Jiafeng，et al.Density based interestpointdetector［J］.Acta Automatica Sinica，2008，34（8）：854-860.（in Chinese）

孫達，唐降龍，劉家鋒，等.基于概率密度的興趣點檢測算法［J］.自動化學報，2008，34（8）：854-860.

［10］Wang Chengliang，Qiao Hesong，Chen Juanjuan.Harris corner detection algorithm based on adaptive fractional differential［J］.Journal of Computer Application，2011，31（10）：2702-2705.（in Chinese）

汪成亮，喬鶴松，陳娟娟.基于自適應分數(shù)階微分的Harris角點檢測算法［J］.計算機應用，2011，31（10）：2702-2705.

［11］Tomasi C，ManduchiR.Bilateral filtering for gray and color images［C］//Proc.Int.Conf.Computer Vision，1998：839-846.

［12］Brox T，Weickert J，Burgeth B，et al.Nonlinear structure tensors［J］.Image and Vision Computing，2006，24（1）：41-55.

Novel corner detection algorithm incorPorating bilateral kernel function

ZHU Li-juan
（Hubei University of Art and Science，Xiangyang 441053，China）

To overcome the problems of insensitiveness to noise and low detection rate in original Harris algorithm，a novel corner detection algorithm based on bilateral kernel function is presented.Firstly bilateral filter is used to replace the Gauss lowpass filter，which improves the robustness of Harris algorithm.Then themulti-scale decomposition is applied to produce segmentation threshold of the true corner and the false corner.Experimental results show that the proposed algorithm can precisely detect comers in images.

Harris algorithm；bilateral filtering；corner detection

TP391.4

A

10.3969/j.issn.1001-5078.2013.05.021

1001-5078（2013）05-0569-04

國家自然科學基金項目（No.20705021）資助。

朱麗娟（1981-），女，碩士，工程師，研究方向為光學圖像處理和光學系統(tǒng)設計。E-mail：cczhulijuan@163.com

2012-10-28