某斜拉橋索力設計要點分析
楊星蕊
(河北省交通規劃設計院,河北 石家莊 050011)
斜拉橋的基本承載構件由梁、塔和索三部分組成。從斜拉橋構成特點可知,其由主梁、拉索、索塔及縱橫聯結系共同受力而形成空間結構體系。因此,斜拉索拉索的索力設計是斜拉橋設計的主要部分。本文以印尼某斜拉橋的索力設計為例,對應用“橋梁博士”軟件實現索力設計的要點進行探討。
1 工程實例概況
本橋主橋為雙塔雙索面預應力混凝土斜拉橋,采用塔墩固結、塔梁分離結構,在塔墩處主梁下設置支座。主橋跨度為185m+370m+185m,邊跨/主跨=0.5;主塔為A型橋塔,橋面以上部分高78.9m,主塔/主跨=0.21。主梁采用肋板式預應力混凝土結構,主梁高2.2m。
2 索力設計
本橋拉索采用雙索面形式,在主塔兩側各有17根拉索,呈扇形布置。在豎橋向橋塔上,拉索索距有1.5m和2m兩種,在順橋向主梁上的索距統一為10m。拉索與水平方向的夾角:左側為24.82°~68.15°,右側為21.598°~67.497°。該橋的斜拉索特性見表1。
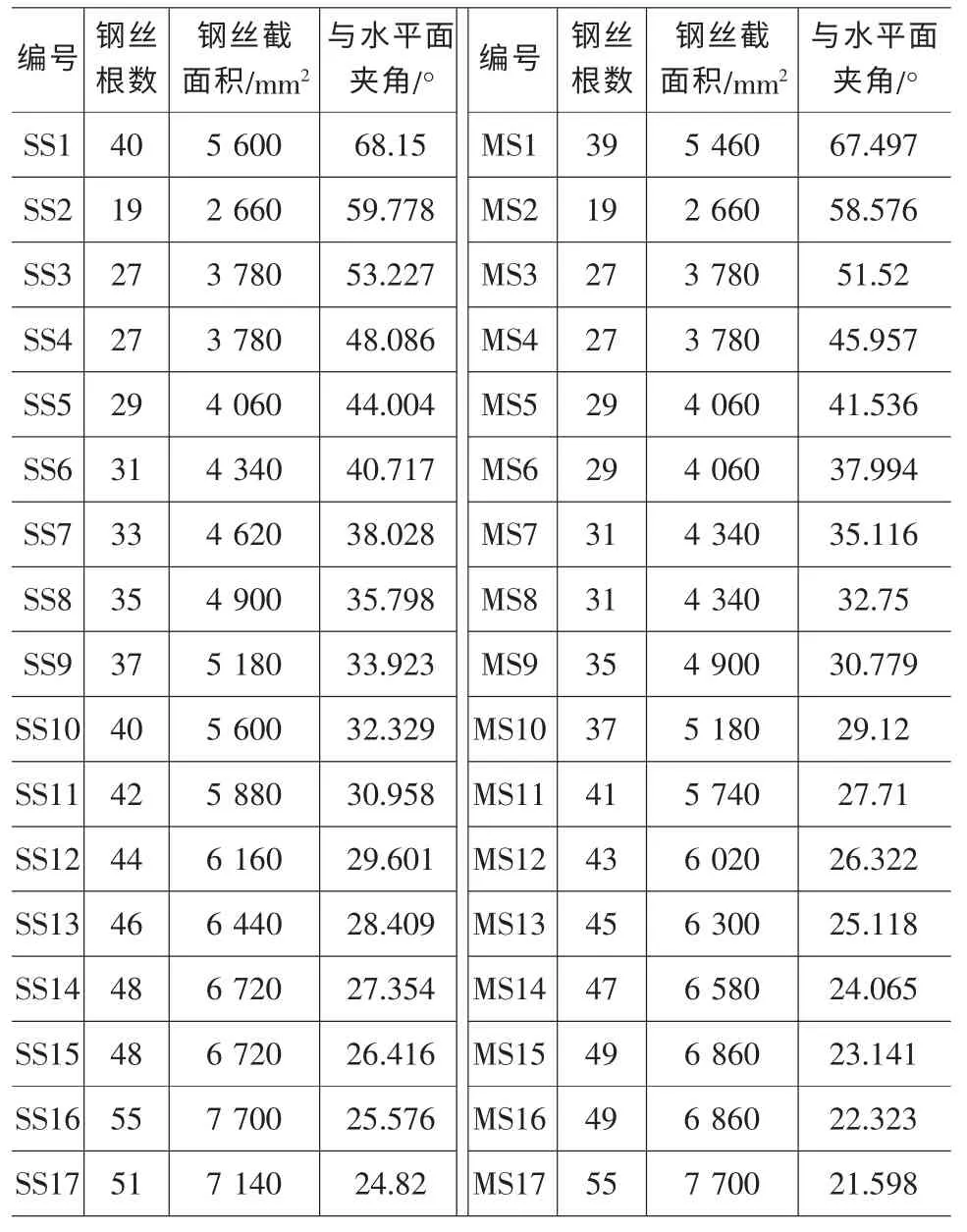
表1 斜拉索特性匯總表
本橋為雙塔斜拉橋,主梁結構為梁格體系,施工方法為在塔柱兩側用掛籃對稱逐段澆筑混凝土。根據該橋的構造和施工特點,采用同濟大學編制的計算軟件“橋梁博士3.03版”建模并進行索力設計和計算(計算模型如圖1所示)。主梁、塔、墩為桿系單元,拉索為索單元。塔墩剛結,主塔處梁與墩豎、縱向鉸結,墩底固定,主梁兩端為滑動支承,全橋劃分424個節點,421個單元。

圖1 “橋梁博士”計算模型
對斜拉索由于自重垂度引起的非線性影響,根據美國公路橋梁設計規范,用修正彈性模量EMOD表征,多次迭代計算由程序自動完成:
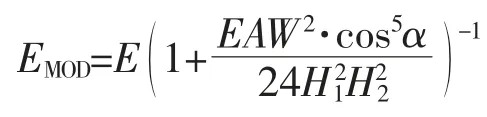
式中:E——拉索的彈性模量,MPa;
W——拉索的總重量,N;
A——拉索的橫截面積,mm2;
H1——拉索變形前的索力水平分量;
H2——拉索變形后的索力水平分量。
由于“橋梁博士”軟件在模擬施工階段的索力調整時,在拉索的張拉階段需要輸入一個初始的索力值,所以在設計中需要對該初始索力進行估算。該索力的計算方法有多種,例如剛性支撐連續梁法、零位移法等,但由于該斜拉橋為中等跨度雙塔三跨塔梁皆對稱的斜拉橋,根據工程經驗采用了等效剛索柔梁法,即將梁的剛度減小100倍、索的剛度增大100倍的恒載作用下的索單元的軸力作為初始索力;“橋梁博士”軟件通過將主梁的彈性模量特征系數改為0.01、將索的彈性模量特征系數改為0.01來實現,并將由此方法計算得出的初始索力值作為“橋梁博士”施工階段拉索張拉的初始值。之后,用“橋梁博士”的調索模塊進行施工階段調索,將索力調到合適值,即在此索力下各施工階段及使用階段,主梁、主塔及拉索的應力都滿足印尼規范的要求,主梁及主塔的位移也較小,在合理范圍內,此索力即為設計初始索力,見表2。
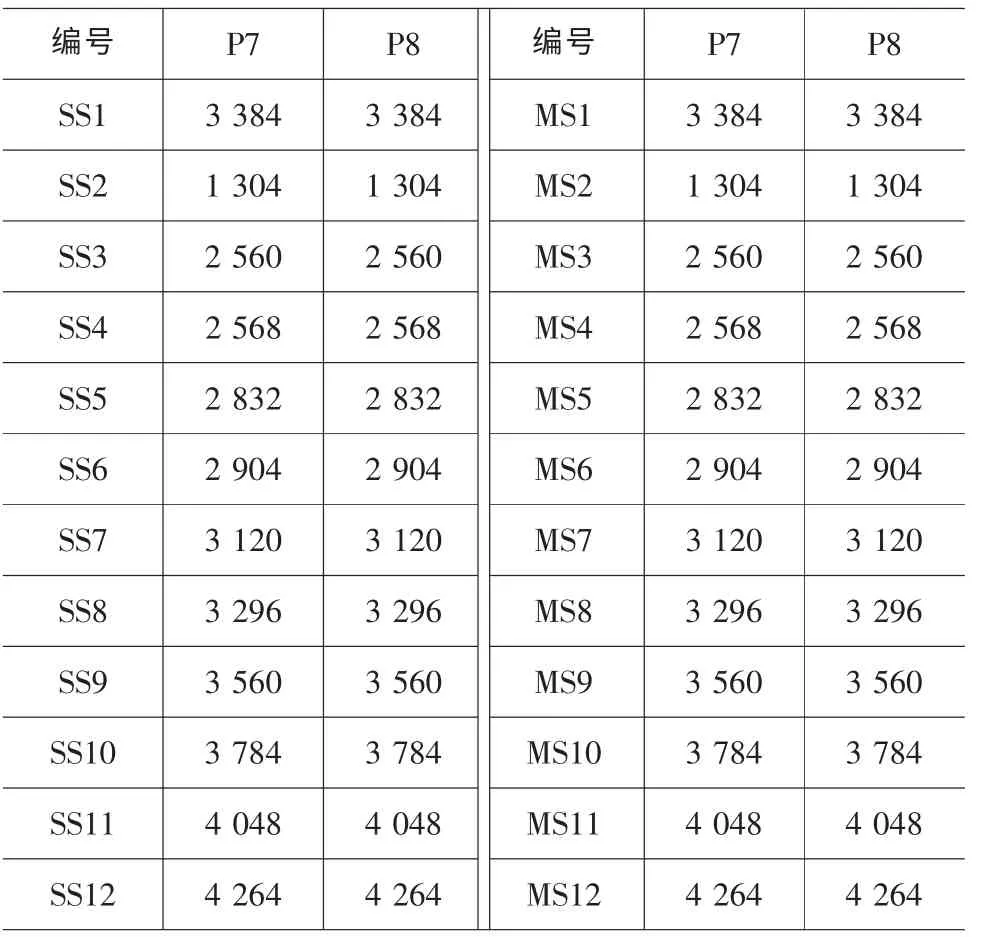
表2 調索后的索力表
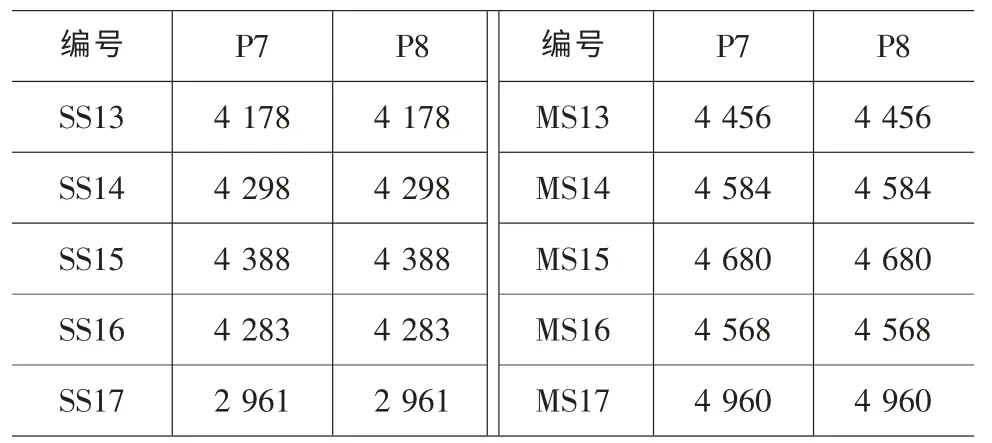
表2(續)
3 結語
斜拉橋的索力設計值受諸多因素影響,如邊跨與主跨之比、索塔高度、拉索傾角、斜拉索的間距等,在設計中應盡量減小拉索的應力變幅。用“橋梁博士”中的調索模塊進行索力設計,其優勢是可以在用戶改變索力值的同時看到主梁的應力變化,經過多次調試使主梁的受力狀態達到設計者想要的水平,并經過調索工具優化后得到合適的設計索力。但值得注意的是,此模塊僅為方便調索的小工具,在程序中輸入合理的初始索力才是關鍵。該初始索力因橋梁構造不同而有不同的計算方法(本文采用的是等效剛索柔梁法)。此外,使用調索模塊時,應根據合理的結構受力狀態調整索力,以得到合適的索力分布。斜拉橋全部拉索合理的索力分布對于結構整體應力狀態很重要。
[1]劉士林,梁智濤.斜拉橋[M].北京:人民交通出版社,2004.
[2]林元培.斜拉橋[M].北京:人民交通出版社,1994.
[3]周孟波.斜拉橋手冊[M].北京:人民交通出版社,2004.
[4]JTG/T D65—01—2007,公路斜拉橋實施細則[S].

