潛艇附體水動力外形優化設計研究

寇冠元，殷 洪，董根金，周友明

(武漢第二船舶設計研究所，武漢430064)

隨著各國海基核戰略的發展，戰略核潛艇所攜載的彈道導彈因為射程所需，具有較大的尺寸，有時甚至會超出耐壓艇體。為了保證潛艇整體型線的光順，一般在艇體彈艙的上部，用上層建筑形成一個整流罩加以覆蓋，俗稱導彈包。導彈包外形的優化設計是潛艇總體綜合設計中的一個重要環節，對潛艇各方面航行性能都有非常重要的影響。許多體型較小的附體都會使潛艇航行阻力大大增加，導彈包所引起的阻力增量更是不容忽視;導彈包引起的潛艇艉部伴流場的不均勻性和不穩定性，將使螺旋槳產生較高的低頻離散噪聲、低頻寬帶噪聲。傳統的設計方法是在借鑒母型艇數據資料的基礎上，憑借設計工程師所掌握的設計知識和實踐經驗對設計艇的需求功能進行分析比較，確定基本艇的導彈包參數和形狀，然后參照母型艇確定控制點和初始型值，再利用現有的CAD軟件采用人機交互方式對導彈包的型線進行協調光順，以及排水量等計算，從而確定基本艇的型線。這種方法高度依賴設計者的經驗，并且得到的最優方案只是相對于初步形成的有限個方案，存在很大的局限性，缺乏一定的合理性和科學性。

針對以上這些問題，運用iSIGHT、FLUENT等商業軟件，以導彈包幾何尺寸為參數，結合CFD、DOE、響應面擬合以及優化算法等技術對導彈包三維曲面進行優化。

1 三維參數化模型的建立

以DARPA SUBOFF模型為主艇體，構建參數化的導彈包方案，設定3個設計變量，分別為導彈包艏過渡段l1，艉過渡段l2，和導彈包舷側長度s，見圖1。

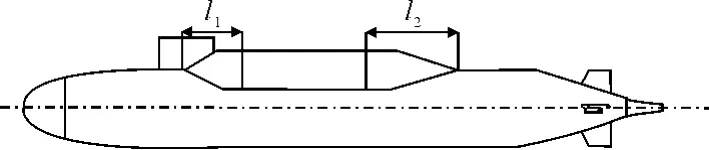
圖1 潛艇主艇體示意

SUBOFF模型由軸對稱體、指揮臺圍殼、艉翼等附體組合而成。其中軸對稱體構成潛艇模型的主艇體，總長4.356 m，進流段長1.016 m，平行中體長2.229 m，去流段長1.111 m(后體端部長0.095 m)，最大直徑為0.508 m。指揮臺圍殼長0.368 m，高0.46 m，頂部為有外凸的橢圓蓋。穩定翼為十字型布置，翼后緣位于4.007 m處，剖面為NACA0020型，見圖2。

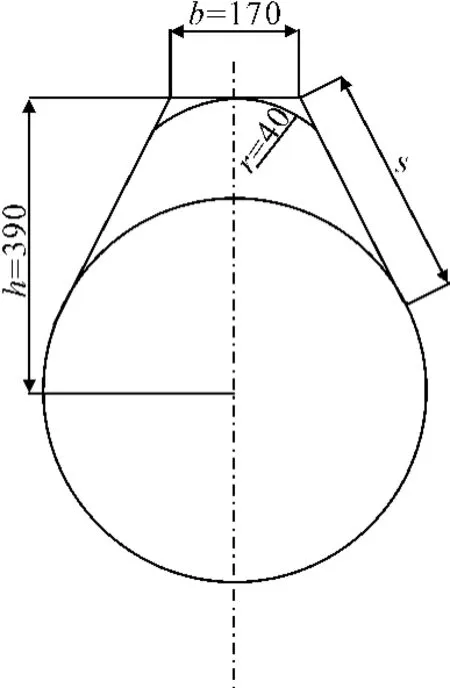
圖2 潛艇橫剖面

圖2 還給出了相應的約束條件，主要包括導彈包上表面距離潛艇回轉體高度h=390 mm，導彈包舷側圓弧倒角r=40 mm，導彈包上表面型寬b=170 mm。依據本文設計變量與約束而建成的潛艇三維模型，見圖3。

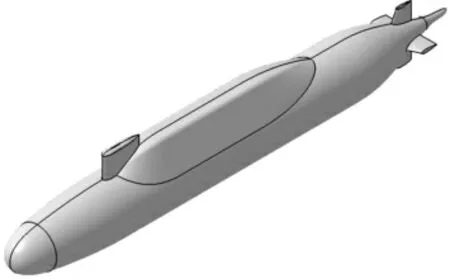
圖3 潛艇三維模型

2 試驗設計

常用的試驗設計方法包括單因素分析法、全因子設計法、正交設計法、中心組合設計法以及拉丁超立方等方法。其中拉丁超立方法在試驗過程中可以大量的取樣，在保證試驗次數大于因素數的前體下，其試驗的次數不受因素數的限制，該方法取樣靈活，可根據需要方便地進行擴充［1］。為此，選用拉丁超立方法構建計算樣本點，同時保證樣本點能夠覆蓋各個參數全部的取值空間。

3 響應面構建逼近函數

運用響應面模型對參變量與設計變量之間的函數關系進行逼近，為后續優化過程的實現提供基礎［2］。構造響應面的方法有很多，其中多項式法兼顧了計算效率與計算精度兩方面，因此將使用二階多項式來構造響應面，其一般的表達形式如下［3］。

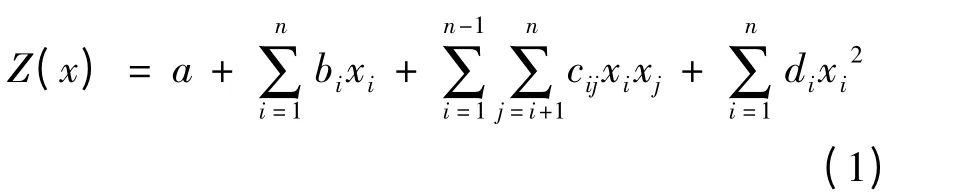
式中:xi——設計變量;

a，bi，cij，di——待定系數;

n——設計變量的個數。

為了進一步提高響應面的擬合精度，上式包含了交叉項。要惟一確定上述方程將需要(n+1)·(n+2)/2組方案。而當方案的數量大于(n+1)·(n+2)/2時，則需要對逼近函數做R2分析［4］。R2的值越接近于1，則表示逼近函數的值與實際值在響應面的設計點處越接近。本文設計變量一共有3個，因此至少需要10個計算方案才能構建出一個二階響應面模型。

4 數值計算方法及驗證

計算區域是一個長為20 m，直徑為10 m的半圓柱體，該圓柱體的軸線和潛艇模型的對稱軸重合，進流面距離艇艏的距離為5 m，相對于潛艇模型的尺寸，該計算域已經足夠大，使流動能夠得到充分的發展，湍流模型采用RNG k-ε。另外，與之相應的邊界條件設置如下。

1)進流面邊界條件為速度入口，各速度分量為u=9.15 m/s，v=w=0 m/s;

2)計算域外側邊界條件為速度入口，各速度分量為u=9.15 m/s，v=w=0 m/s;

3)出口邊界條件為壓力出口，參考壓力為0;

4)艇表面邊界條件為無滑移壁面，即u=v=

w=0 m/s;

5)流域對稱面的邊界條件為symmetry。

運用這種方法，對全附體SUBOFF模型進行計算，得到的阻力位407.32 N，而試驗值則是410.88 N，兩者偏差為0.86%，說明本文數值計算是可靠的和有效的。

5 優化結果與分析

各設計變量的取值范圍分別為200≤l1≤1 000，200≤l2≤1 000，190≤s≤307.910 7，樣本點見表1。其中0號方案為原始方案，1～15號方案是依據拉丁超立方試驗設計規則制定的樣本點，這些樣本點已覆蓋了所有取值空間。

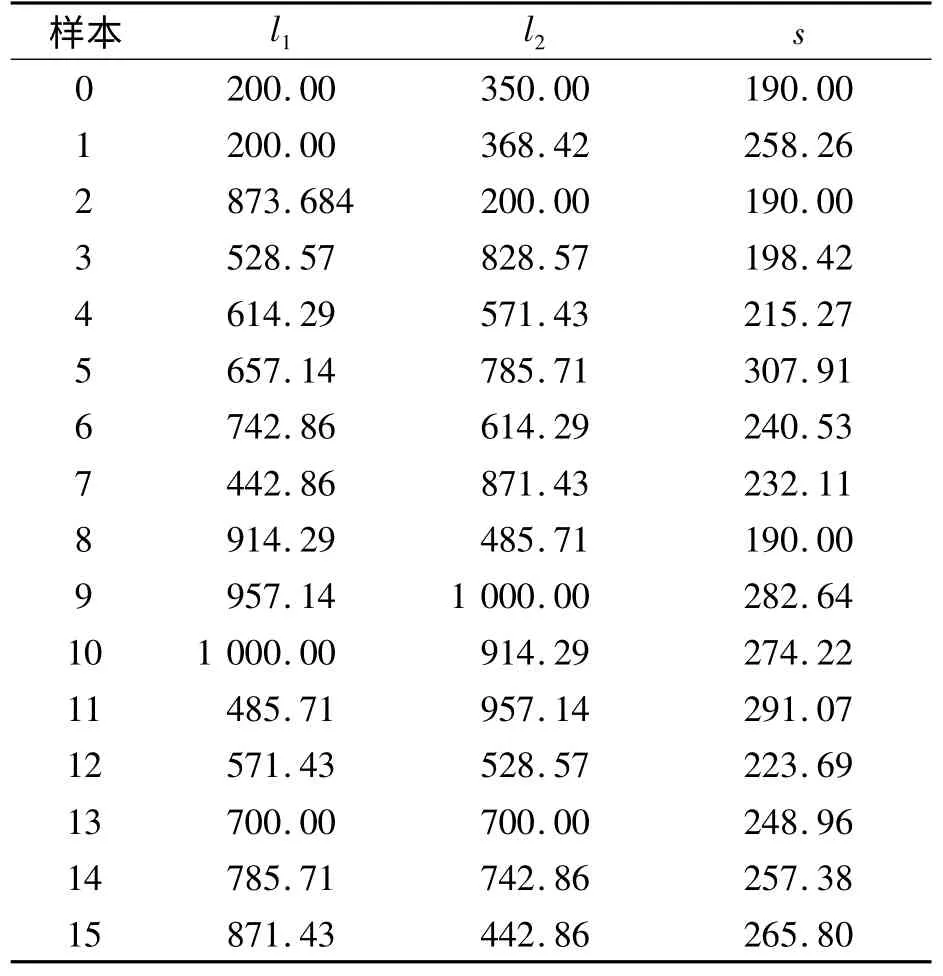
表1 計算方案 mm

另外，本文優化算法將選用模擬退火算法，采取二階段迭代優化策略對導彈包外形進行優化，其中第二階段較第一階段的設計樣本點數量有所增加。具體優化過程如下。

1)選取1～10號樣本點構造二階響應面以實現目標函數的近似建模，保留11～15號樣本驗證響應面近似模型的精度，值得注意的是1～10號樣本點已經覆蓋全部的取值空間;

2)調用iSIGHT中的模擬退火算法對響應面近似模型進行優化，找到近似最優點;

3)啟動CFD求得最優點處的真實計算值，并比較最優點與該值之間的偏差，至此完成第一階段的優化;

4)將11～15號樣本點與第一階段最優點的CFD計算值加入到響應面，對其進行更新;

5)重新啟動模擬退火算法對更新后的響應面進行尋優，找到近似最優點，并比較該點處的近似值與CFD計算值之間的偏差，至此完成第二階段的優化。

計算采用的來流速度v=9.15 m/s，以滿足雷諾數Re＞107。由于模型及流動的對稱性，計算只在對稱面的一側內進行以提高計算效率。

5.1 第一級優化

運用1～10號樣本點的CFD計算值構造二階響應面，求得R2=1，表明響應面在各樣本點處的擬合值與CFD計算值相等。運用響應面預報11～15號樣本點的阻力，并與計算值進行對比，結果見表2。

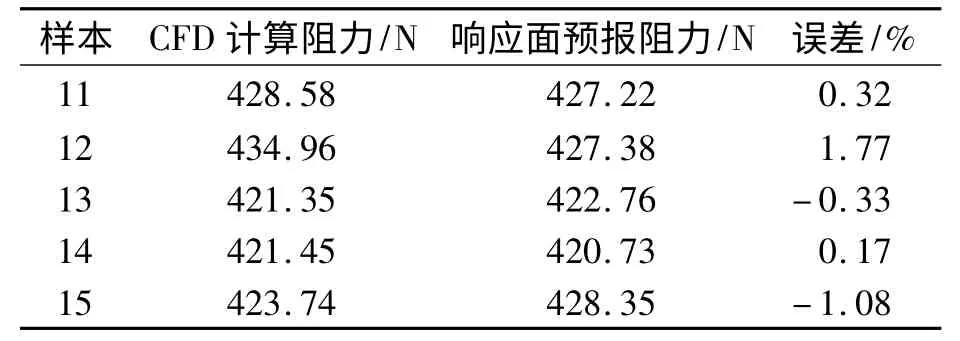
表2 響應面擬合結果

見表2，12號樣本的誤差相對較大，但是總的來說擬合結果都在許可誤差范圍內，表明該方法能較好地預報帶導彈包潛艇的航行阻力。

使用模擬退火算法對響應面進行優化，優化收斂過程曲線見圖4。

迭代次數共815次，優化結果為411.88 N，對應設計變量取值為l1=1 000 mm，l2=878.35 mm，s=307.91 mm。將該組設計變量的取值定為第16號計算樣本點。啟動CFD，求得16號樣本點的阻力為419.42 N，兩者絕對誤差有7.54 N，相對誤差為1.83%。

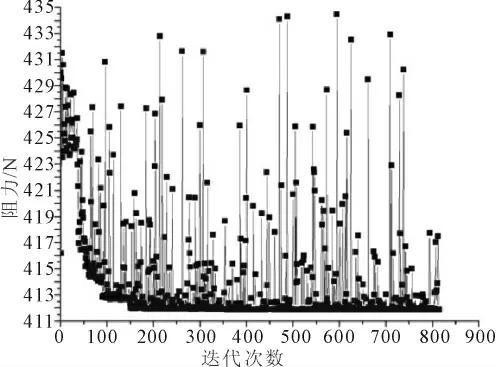
圖4 第一階段優化過程曲線

5.2 第二級優化

使用11～16號樣本點的CFD計算值對響應面近似模型樣本進行更新，此時R2=0.927，相較于第一級優化響應面R2值有所下降，這是由于樣本數增加引起。為了驗證更新后響應面模型的擬合精度，本文再另外設計3組樣本，編號17～19，具體參數設置見表3，結果見表4。

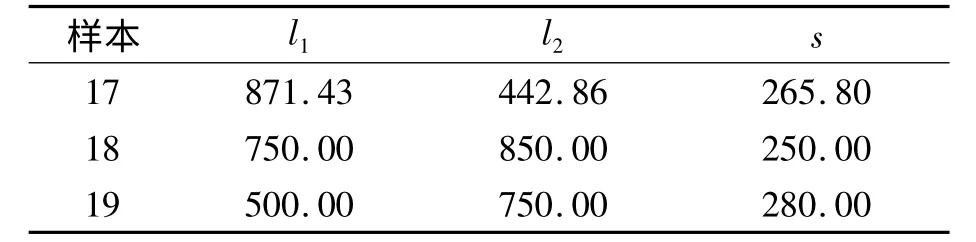
表3 各樣本參數 mm

表4 各樣本擬合結果

增加了新的樣本點以后，盡管R2的值下降，但是擬合精度卻提高了，最大偏差不超過1%。調用iSIGHT中的優化模塊對更新后的響應面模型進行優化。模擬退火算法在第二階段的優化過程收斂曲線見圖5。

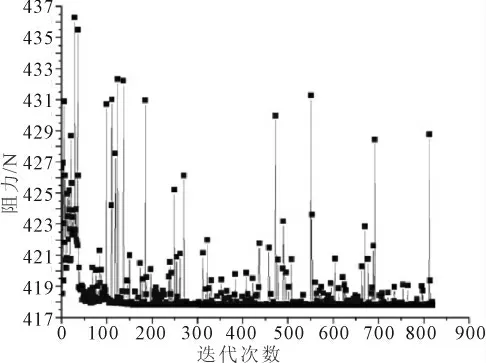
圖5 第二階段優化過程曲線

經過優化得到潛艇阻力為417.8 N，對應的設計變量分別為l1=928.32 mm，l2=913.81 mm，s=247.98 mm，該點處的CFD計算值為416.8 N，兩者絕對誤差為0.97 N，相對誤差為0.26%。增加了構造響應面的樣本點數量之后，優化結果更加精確了。

表5列出了最終的優化結果與原始方案(即0號樣本點)各參數和CFD計算阻力的數據。

表5 原方案與優化方案各項數據

經過第二階段的優化后潛艇總阻力下降了13.2%。優化前后三維模型的對比見圖6。從外形來看，導彈包的艏、艉過渡段都延長了，同時舷側張角略有增加。

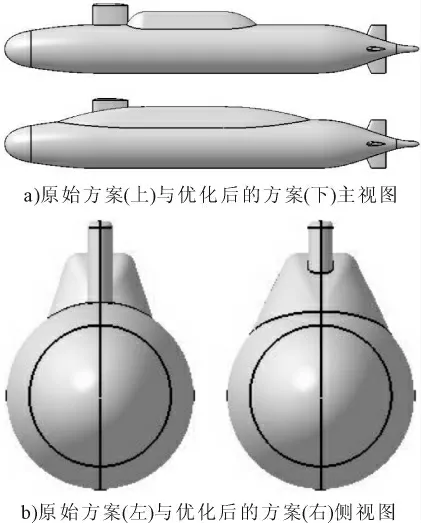
圖6 優化前后三維模型

從阻力產生機理分析，增加艏、艉過渡段的長度，使導彈包處的型線更加光順，能有效地抑制邊界層分離，減小由于邊界層分離產生的粘壓阻力。雖然這樣使總的濕表面積有所增加，摩擦阻力增大，但是其增量相較于邊界層分離產生的阻力仍是小量。

運用iSIGHT繪制的阻力在最優點處隨各參數變化的曲線見圖7，此圖進一步驗證了阻力變化的規律。

本文運用19個樣本點即找到了使潛艇阻力最小的一組導彈包設計參數。若采用全因子排列方法，假設每個變量取4個狀態，則需要64(43)個樣本點。表明本文的方法不僅能有效地進行尋優，同時能提高整個優化過程的效率。

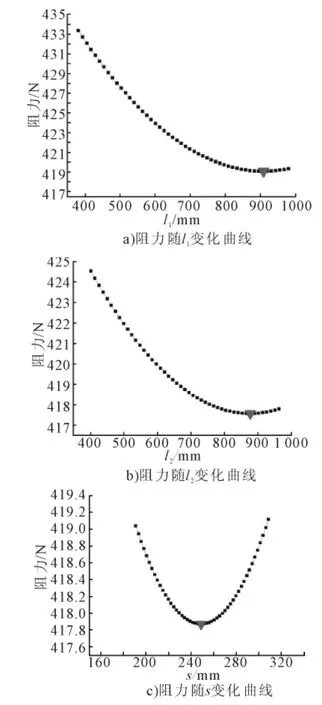
圖7 目標值隨各參數變化曲線

6 結論

1)優化后的方案與原始方案相比，艏、艉過渡段更長，舷側張角更小，總阻力下降了13.2%;

2)在最優點附近，潛艇總阻力隨3個設計變量均呈現先減小后增大的趨勢。這是因為隨著設計變量增大，表現為形狀阻力減小及摩擦阻力增加，總阻力在一定范圍內取得最小值;

3)引入響應面的優化方法能減少計算樣本點的數量，提高優化過程的效率;

4)運用本文提出的方法，能有效地對導彈包外形進行優化，使潛艇航行總阻力減小;同時還能夠精準、快速地預報潛艇配備不同方案導彈包時的阻力，為日后新方案的導彈包設計提供參考。

［1］王 錄.軸流式葉輪機械葉片氣動數值優化設計研究［D］.北京:中國科學院工程熱物理研究所，2010.

［2］王曉鋒，席 光，王尚錦.響應面方法在葉片擴壓器優化設計中的應用研究［J］.工程熱物理學報，2003，24(3):33-36.

［3］劉杰雪.基于響應面法的集裝箱船優化設計研究［D］.天津:天津大學建筑工程學院，2008.

［4］黃 靚，李景銀，高 遠.基于響應面法的風力機翼型氣動優化設計［J］.流體機械，2011，39(2):21-24.