基于磁流變阻尼器的車輛懸架振動優化控制＊

趙 強 米 磊 尹佳星

（東北林業大學交通學院 哈爾濱 150040）

0 引 言

近年來磁流變（MR）阻尼器作為智能型減振器，在車輛懸架振動的半主動控制領域中日益得到重視.文獻［1］研究了配備MR 阻尼器的1／4車懸架振動的神經網絡半主動控制，文獻［2］根據MR 阻尼器的Bouc－Wen模型研究了1／4車懸架振動的開關控制.然而，由于MR 阻尼器所固有的高度非線性特性，當MR 阻尼器用于振動控制時，需要解決如何由控制規律所決定的控制力得到其輸入電壓的逆向問題.目前，通常的解決方案是根據開關控制律來調整輸入電壓［3］以及開關最優控制算法［4］.由于MR 阻尼器的輸入電壓只能在最小值和最大值之間切換，這樣就沒有實現控制信號的連續可調，必然會限制MR 阻尼器的性能.

鑒于神經網絡可以逼近任意的非線性函數，本文提出運用神經網絡技術建立非線性控制裝置MR 阻尼器的神經網絡模型來模擬其逆向動特性，同時與LQR 主動控制方法結合形成閉環回路對車輛懸架系統進行半主動控制研究.運用該方法能夠通過逆模式神經網絡得到連續的控制電壓，從而實現阻尼力的連續可調，充分發揮MR阻尼器的智能特性，從而實現控制車輛懸架系統振動響應的目的.

1 MR 阻尼器神經網絡逆模式控制的分析方法

1.1 控制策略

圖1為車輛懸架系統在路面激勵的作用下進行MR 阻尼器神經網絡逆控制的整體框圖.控制器根據車輛懸架系統的振動響應計算出期望的控制力，期望控制力連同阻尼器位移一起進入到MR 阻尼器的神經網絡模型，它的輸出就是在當時懸架系統的振動響應下，為了使MR 阻尼器產生與期望控制力相對應的控制電壓，該電壓輸入給MR 阻尼器使之產生接近期望控制力的輸出力作用到車輛懸架系統，從而降低其振動響應.

1.2 MR 阻尼器半主動約束

本文采用Spencer 等提出的修正的Bouc－Wen模型來描述MR 阻尼器的力學特性，該模型引入2個內變量，構造了包含14個待定參數的微分方程模型［5］.

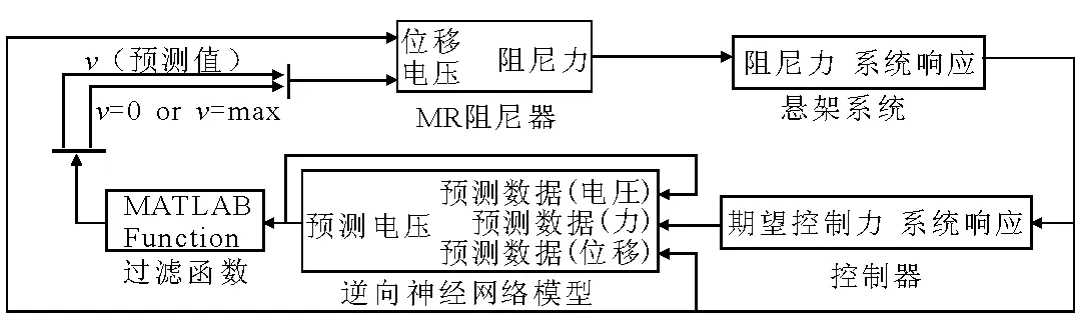
圖1 控制策略框圖

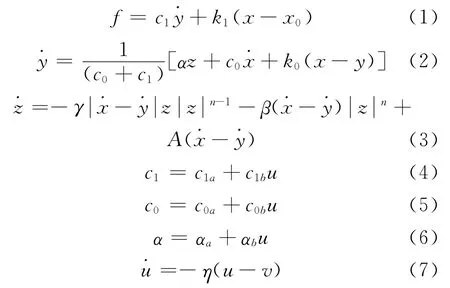
式中：x 和f 分別為MR 阻尼器的位移和阻尼力；c1a，c0a，αa為無電壓時的系數；c1b，c0b，αb為隨電壓變化的系數；u為聯系f 和v 的中間變量；v 為阻尼器的驅動電壓；γ，β，A 為遲滯特性相關系數；n為指數系數，一般取2.式（1）～（7）描述的MR 阻尼器力與位移以及力與速度的關系曲線見圖2.

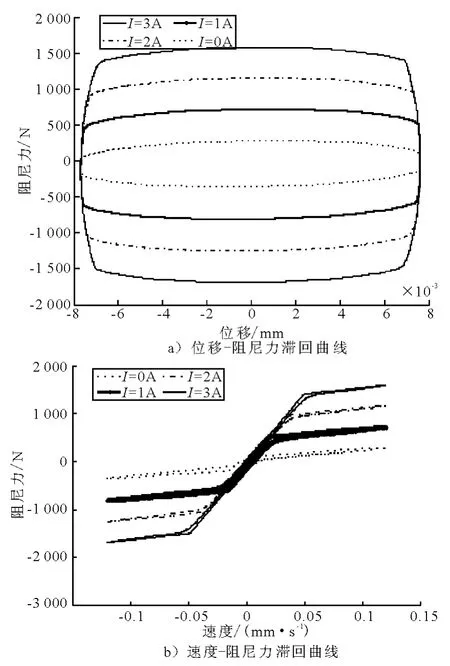
圖2 MR 阻尼器位移－阻尼力、速度－阻尼力滯回曲線

從圖2b）可看出，MR 阻尼器所能提供的阻尼力位于阻尼力－活塞速度平面的第I，III象限，而不能如主動控制元件那樣提供4個象限的力，也就是說只有當期望控制力與活塞速度兩者符號相同時，磁流變阻尼器才能輸出跟蹤期望控制力的阻尼力，可描述為

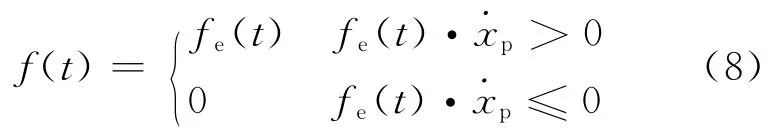
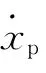
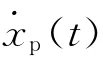
1.3 MR 阻尼器的逆向神經網絡模型

MR 阻尼器逆向神經網絡預測實質上是由下列方程所示的輸入輸出之間的非線性映射.

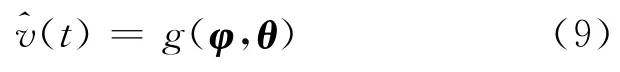
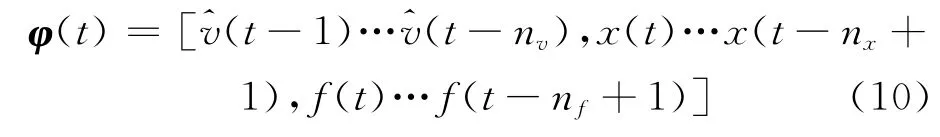
其中：nv，nx和nf分別是輸入電壓、位移和阻尼力的時間步長數.圖3為其訓練框圖.

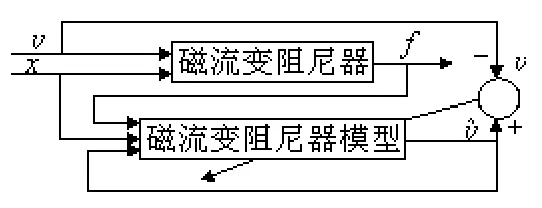
圖3 MR 阻尼器的逆向神經網絡模型訓練框圖

由Kolmogorov逼近定理可知，具有單隱層的（修改）BP神經網絡可以逼近任意具有有限間斷點的非線性函數，因此本文選用一個3 層BP神經網絡來描述MR 阻尼器的逆向動特性.網絡的輸入層有9個節點，由3個連續時間步長的輸入電壓、位移和阻尼力組成（nv＝nx＝nf＝3）；隱層有20個節點，輸出層有1個節點，是當前時刻的控制電壓.此外，隱層和輸出層的傳遞函數分別采用tansig函數和purelin函數，以目標輸出和網絡輸出的均方誤差為網絡性能函數，網絡訓練函數采用標準梯度下降算法traingd函數（修改）.訓練和驗證數據選取如下位移和輸入電壓由Gaussian白噪聲生成，頻率范圍分別是0～3 Hz和0～4Hz，阻尼力由式（1）～（7）求得.以500Hz采樣頻率對上述生成數據采樣20s，共產生10000個數據對用來對該逆模型進行訓練和驗證，在使用中，采樣數據要進行規則化處理（均值為零方差為1）.圖4所示為控制電壓目標值和預測值的比較，從圖中可看出，預測值能夠很好的跟蹤目標值，說明網絡訓練比較成功，具有很強的泛化能力.

1.4 車輛懸架動力學模型

為了簡化控制模型，突出研究問題的主要方面，圖1中的車輛懸架系統采用簡化的1／4車二自由度懸架系統模型，見圖5.

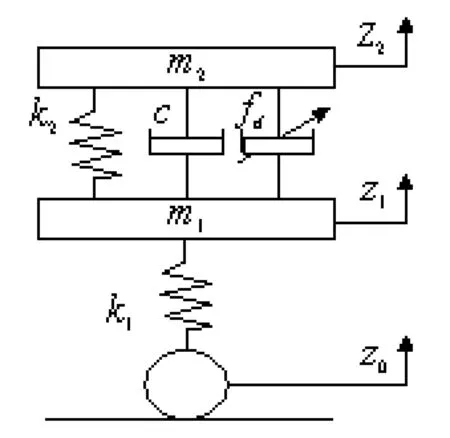
圖5 1／4車二自由度車輛懸架系統模型

由圖5得懸架系統的動力學方程

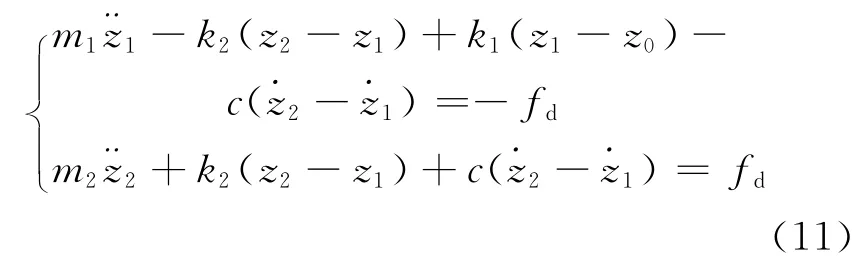
式中：m1為半主動懸架非簧載質量，kg；m2為半主動懸架簧載質量，kg；k1為輪胎徑向剛度系數，N／m；k2為懸架剛度系數，N／m；c為磁流變阻尼器的無場阻尼系數，N·s／m；z2為車身簧載質量的垂直位移，m；z1為車身非簧載質量的垂直位移，m；z0為路面激勵，m；fd為磁流變阻尼器的有場阻尼力，N.

2 最優控制器的設計

將訓練完成的MR 阻尼器神經網絡逆向模型用于實現控制算法所解算出的控制力的要求，為了盡可能的降低車身垂直加速度 懸架動撓度及輪胎動載荷使車輛獲得較高的行駛平順性和操縱穩定性，同時不消耗太多能量，本文綜合考慮懸架各種性能指標，采用LQR 算法［6］進行控制器的設計.

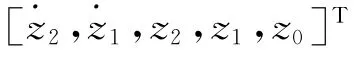
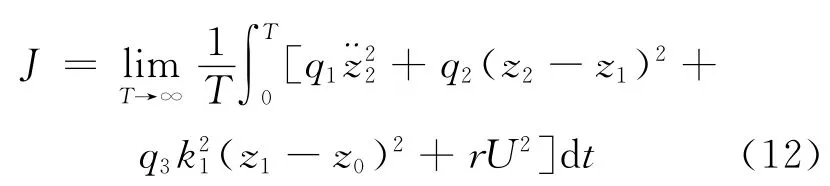
式中：q1，q2，q3為加權矩陣q系數，決定著懸架系統的性能；r為約束系數.加權系數可以書寫為矩陣形式

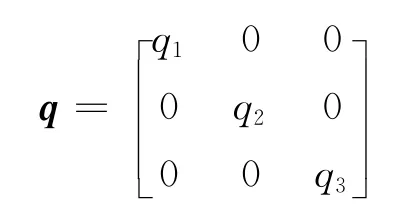
則性能指標公式轉換為

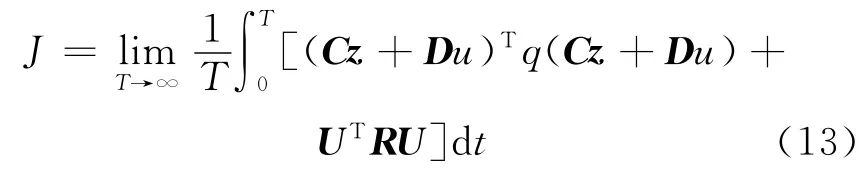
按照矩陣的運算規律，將上式展開可得

設Q＝CTqC，N＝CTqD，R＝r＋DTqD，則式（14）可寫為

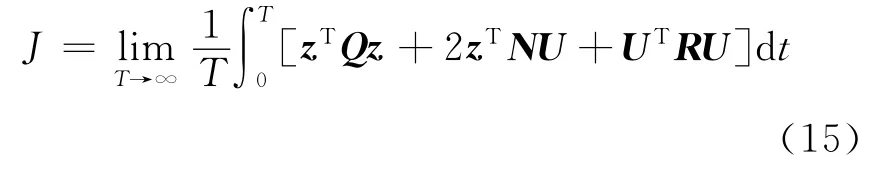
確定車輛參數和加權系數之后，運用黎卡提方程求出反饋增益矩陣K.

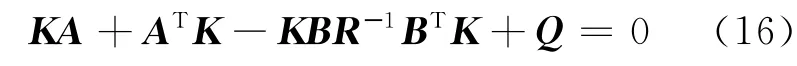
求出增益矩陣K 之后，最優控制器的設計基本完成.根據任意時刻的反饋狀態變量 z（t） ，就能得出t時刻作動器的最優控制力 U（t） ：

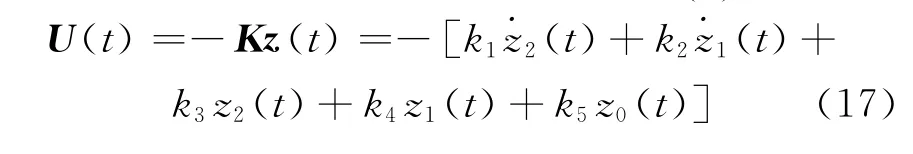
3 仿真分析

3.1 減振效果分析

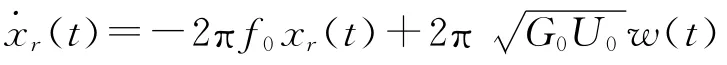
為更好地分析本文提出的MR 阻尼器神經網絡逆控制的減振效果，將其與被動懸架作比較.圖6為懸架加速度 動撓度以及輪胎動載荷的仿真結果，由圖可知，基于神經網絡逆控制的懸架系統相比于被動懸架性能有明顯的改善，表1為其相應的均方根值.由表1 可知，基于MR 阻尼器神經網絡逆模型控制的半主動懸架加速度較被動懸架下降20.72%，動撓度下降了22.11%，輪胎動載荷下降了10.67%，有效降低了車身振動對人體的影響，顯著提高了車輛懸架系統的動態舒適性.

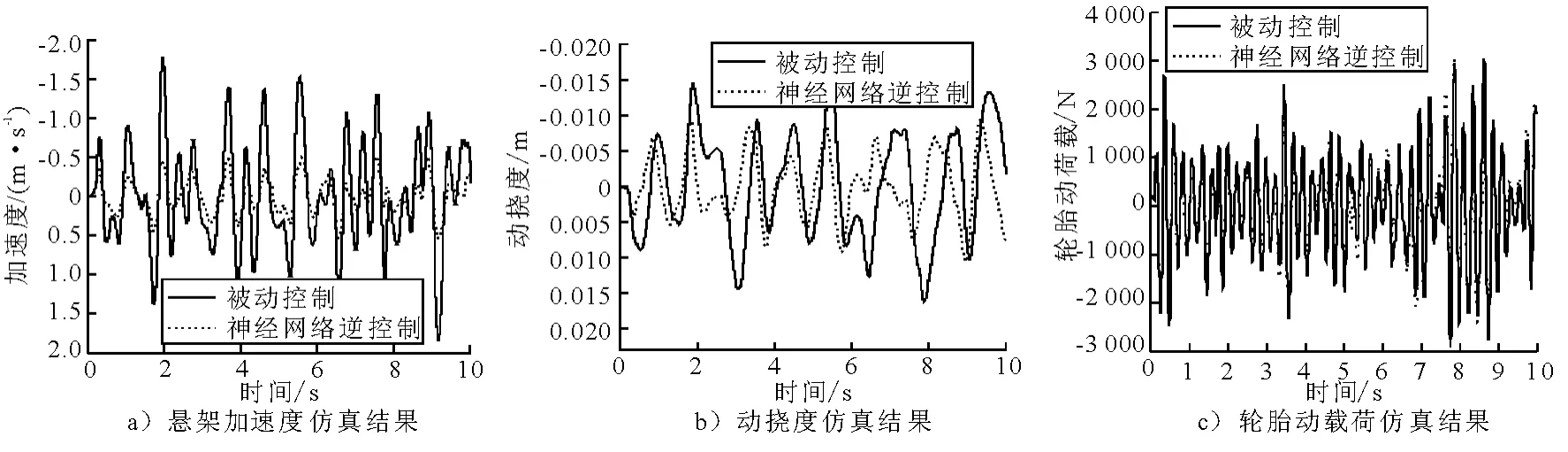
圖6 仿真結果

3.2 頻域減振分析

隨機路面激勵下的車輛懸架加速度功率譜密度低頻放大（20 Hz）圖見圖7.從中可以看出，神經網絡逆模型控制作用下的車輛懸架加速度在高頻處因變頻干擾基本和被動懸架相同，但在車身共振（1～1.5 Hz）和人體垂向最敏感（4～12.5 Hz）［8］這2個低頻范圍內，神經網絡逆模型控制有效地降低了車輛懸架加速度.在1～1.5 Hz區間，神經網絡逆模型控制較被動控制加速度改善不少，而在4～8Hz這個人體內臟器官最易產生共振的頻率范圍內，神經網絡逆模型控制較被動控制加速度也有顯著降低，進而減輕乘員乘坐的不舒適性.

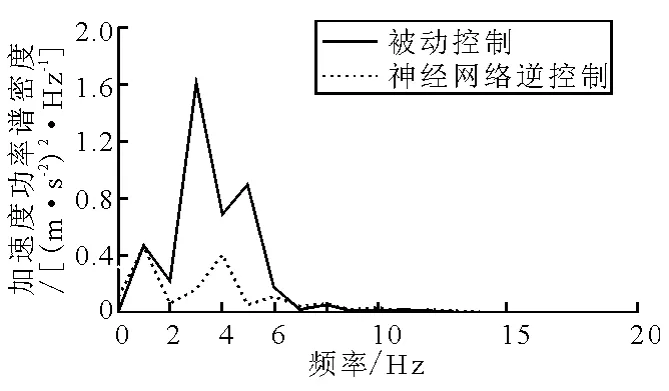
圖7 加速度功率譜密度低頻放大圖

圖8所示為MR 阻尼器的輸入控制電壓以及由此產生的阻尼力，為了比較還給出了LQR主動控制的期望控制力，從圖中可見，MR阻尼器實際出力跟隨期望控制力較為接近.

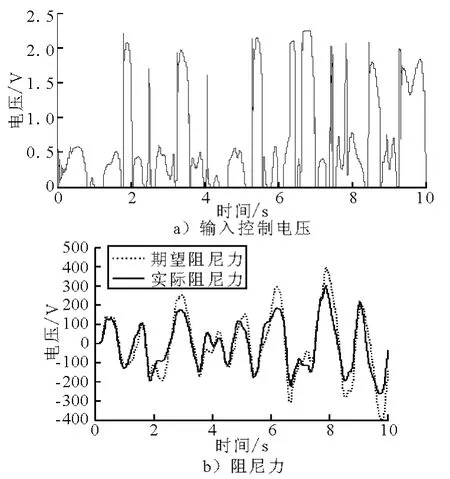
圖8 MR 阻尼器的輸入電壓及輸出阻尼力

4 結 論

1）針對MR 阻尼器的高度非線性特性，運用神經網絡模型來模擬MR 阻尼器的逆向動特性，該神經網絡模型直接提供了為產生由最優控制算法計算出的期望控制力所需連續輸入電壓的估計手段.

2）時域和頻域內的數值仿真結果表明：在控制策略中通過引入MR 阻尼器的逆向神經網絡模型，可有效的改善車輛懸架系統的性能，同時使MR 阻尼器的連續調節主動控制成為可能，為進一步的工程應用奠定了理論基礎.

［1］GUO D L，HU H Y，YI J Q.Neutral network control for semi－active vehicle suspension with a Magnetorheological Damper［J］.Journal of Vibration and Control，2004，10（3）：461－471.

［2］YAO G Z，YAP F F，CHEN G，et al.MR damper and its application for semi－active control of vehicle suspension system［J］.Mechatronics，2002 （12）：963－973.

［3］DYKE S J，SPENCER B F.A comparison of semiactive control strategies for the MR damper［J］.Intelligent Information Systems，1997（8－10）：580－584.

［4］DYKE S J，SPENCER B F，SAIN M K.Modeling and control of magneto－rheological dampers for seismic response reduction［J］.Journal of Smart Materials and Structures，1996（5）：565－575.

［5］SPENCER B F，DYKE S J，SAIN M K，et al.Phenomenon logical model of a magneto－rheological damper［J］.ASCE Journal of Engineering Mechanics，1996（3）：1－23.

［6］趙 亮，文桂林.基于磁流變阻尼器的車輛半主動懸架最優控制的研究［J］.汽車工程，2008，30（4）：341－343.

［7］俞 凡，林 逸.汽車系統動力學［M］.北京：機械工業出版社，2005.

［8］DAVE C，喻 凡.車輛動力學及其控制［M］.北京：人民出版社，2004.