快速路路段通行能力非參數估計方法＊

邵長橋

（北京工業大學交通工程北京市重點實驗室 北京 100124）

0 引 言

在以往的研究中，研究人員往往把通行能力作為道路設施一個確定的參數來研究的［1］.但是，越來越多的研究發現，道路設施通行能力具有一定的隨機性.近年來提出的多相位交通流理論關于交通狀態之間的“躍遷”現象為此觀點提供了理論支持［2］；此外，研究人員對交通流的“躍遷”、“通行能力二值”現象［3－4］與交通中斷（連續流設施設上出現排隊）等相關研究成果也揭示了通行能力的隨機性特性.

上述研究表明，傳統的通行能力定義沒有考慮交通流隨機特性的影響，其在評價交通設施和交通管理等方面的應用不足越來越明顯［5－7］.為此，研究人員提出了基于交通中斷概率意義下的道路通行能力定義：給定的道路、交通條件下，均勻路段上相應于可接受的交通中斷概率水平下的期望小時流率［8］.為了估計基于交通中斷概率意義下的道路通行能力，Lily等人［9］從理論上探討了應用壽命數據中的“乘積限”方法估計通行能力分布的可行性，但并沒有針對交通數據特點給出通行能力具體估計方法和步驟.本文結合交通流中斷特性，給出了基于“乘積限”方法的通行能力估計方法和步驟，并應用仿真數據對估計方法進行了驗證.

1 交通流中斷特性分析

交通流中斷（breakdown）描述的是交通流從非擁擠狀態到擁擠狀態的一種交通狀態轉變現象，見圖1.當發生交通流中斷時，交通流平均運行速度會突然下降，并且處于“中斷”狀態運行的交通流運行速度低于某給定的閾值（根據北京市三環快速路段交通觀測數據統計結果可以發現，處于交通中斷狀態的交通流，車流運行平均速度很少超過25km／h；而處于非擁擠狀態時，車流平均運行速度大部分保持在40km／h 以上），在交通流中斷前后的2個觀測時段內，流率變化較大，分別為1050～2070pcu／h和1610～2090pcu／h.

2 可行性分析

為了說明壽命數據分析方法用于估計道路通行能力分布的可行性，Brilon等人對壽命數據分析和通行能力分析作了對比研究，并運用“乘積限方法”（product limit method）估計道路通行能力分布.

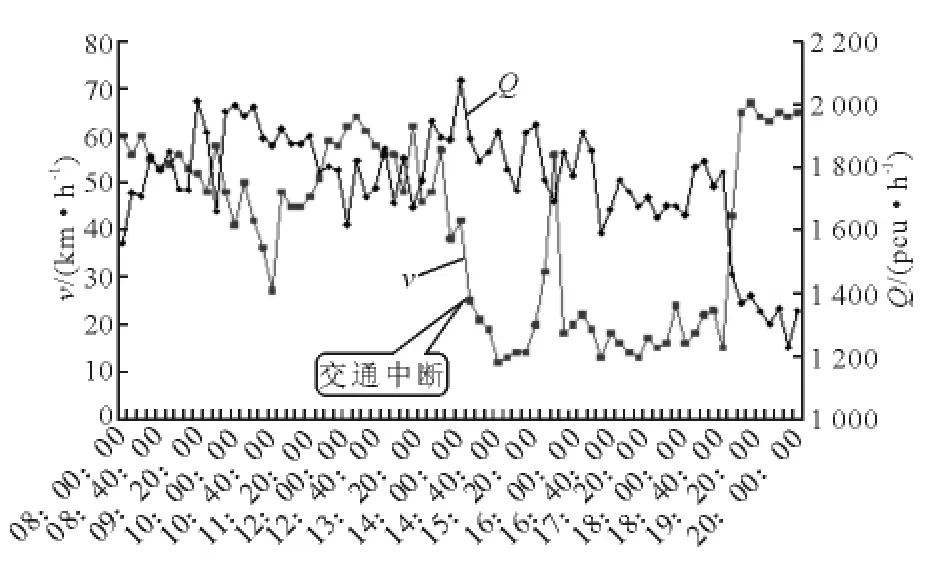
圖1 流率與速度時間序列圖

生存分析中的“乘積限方法”是一種非參數方法［10］，其公式為

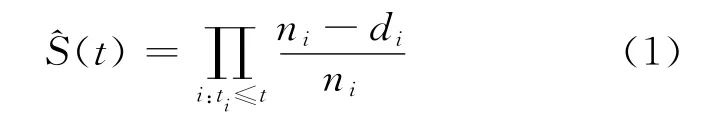
為了把模型（1）“移植”到通行能力分布估計中，類似定義生存函數一樣，定義“在流量達到q時沒有發生交通中斷的概率”為

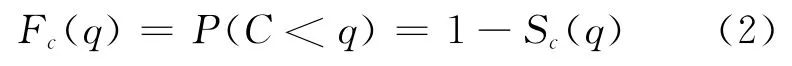
式中：Fc（q）為通行能力C 的分布函數；C 為通行能力，為隨機變量，pcu／h；q為流量，pcu／h.相應的通行能力分布“乘積限”估計為

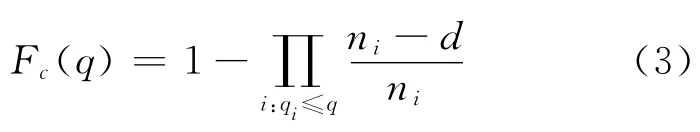
式中：Fc（q）為通行能力C 的分布函數；qi為在該流量水平下，觀測到交通中斷發生；di為在流量為qi時，發生交通中斷的次數，i＝1，2，…，k＋1；ni為在觀測的樣本中，流量q≤qi時，沒有發生交通中斷的次數，i＝1，2，…，k＋1.

從上述模型“移植”過程來看，存在著以下問題：（1）對于壽命數據，個體死亡時間ti（i＝1，2，…，n）是可以確切知道或觀測到的；而對于交通流來說，交通中斷發生往往滯后于交通需求（即交通需求達到某值后，并不是馬上發生交通流中斷），并且交通觀測往往是以一定的統計時間間隔為統計單元（如5，10，15 min）等，不能確切知道交通中斷發生時間和對應的真實流量；（2）壽命數據中的“截尾”現象不能完全解釋交通現象.正如1）所敘，交通中斷存在滯后性，如果按照壽命數據中“截尾”的定義，則觀測到的交通中斷發生時對應的流量都是“截尾”數據；（3）相對而言，交通中斷現象是“小概率”事件.在交通工程中，研究交通中斷現象，常以5min作為統計時間間隔，則1d有288個統計觀測數據，（受交通早晚高峰的影響）一天中觀測到交通中斷發生往往只有2次，并且只有交通中斷發生前的一組數據可以提供交通中斷發生時對應的流量信息.

因此，考慮上述交通數據特點，本文給出了只應用交通中斷發生前一個統計時間單元交通流量信息來估計通行能力的方法和步驟.

3 道路通行能力壽命表分析方法

基于上述分析，運用壽命數據中壽命表方法和理論，給出通行能力分布估計步驟如下.

1）將所有觀測到的交通中斷發生前一個統計時間單元內的流量劃分為k＋1 個區間：Ij＝［aj－1，aj），（j＝1，2，…，k＋1）.其中，a0根據觀測數據確定（在該流量下，不發生交通中斷，可取a0＝min｛qi，i＝1，2，…，N｝－q0，qi為第i 次交通中斷發生時前一個統計時間單元觀測到的流量，N為觀測到的總的交通中斷次數，q0為某個大于0的常數；aj＝a0＋h×j，j＝1…，k，其中，h 為區間長度（根據通行能力估計的精度，可取h＝50），ak＋1＝∞.

2）計算統計量 記：Nj＝在觀測到的N 次交通中斷中，流量q＞aj－1時交通中斷的次數；dj＝為觀測到的N 次交通中斷中，流量在Ij＝［aj－1，aj）內發生交通中斷次數；P（j）＝Pr（在流量q＜aj時沒有發生交通中斷）；P（j）＝Pr（在流量q＜aj時，沒有發生交通中斷｜在流量q＜aj－1時沒有發生交通中斷）；q（j）＝Pr（在流量aj－1≤q＜aj時，沒有發生交通中斷｜在流量q＜aj－1時沒有發生交通中斷）.

則由上述定義以及a0與ak＋1取值可知：

P（0）＝P（在流量q＜a0時沒有發生交通中斷）＝1

P （k＋1）＝Pr（在流量q≤ak＋1時沒有發生交通中斷）＝0

并且

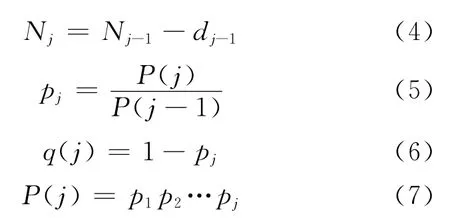
3）估計通行能力分布 由概率論知識，在流率區間I1，I1，…，Ik上觀測到的交通中斷次數d1，d2，…，dk服從多項分布：

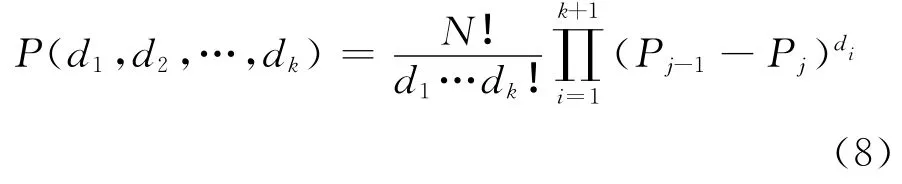
把式（6）與式（7）代入式（8），則有

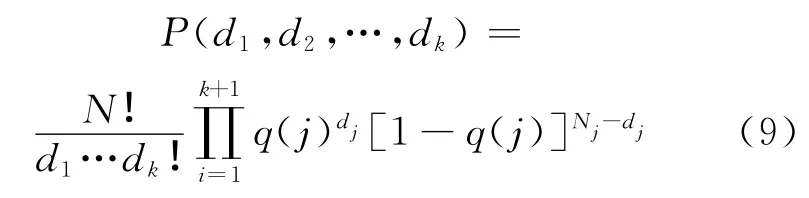
式中：Nj＝n－d1－…－dj－1.應用極大似然估計，可求得

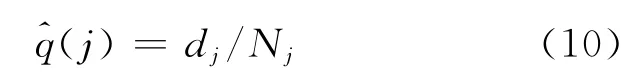
P（j）的極大似然估計為

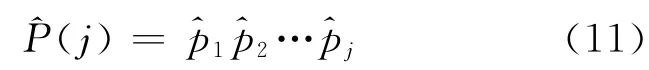
為了便于應用式（3）或式（11）估計通行能力的分布，仿照壽命表方法編寫通行能力“壽命表”，見表1.

表1 道路通行能力“壽命表”

4 基于交通中斷概率的通行能力定義和計算

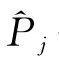
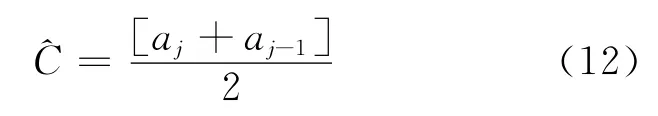
5 仿真驗證

為了說明如何應用本文介紹的程序和方法估計通行能力分布，結合北京市三環路某內環路段實際交通流觀測數據，對交通中斷概率分布和通行能力分布估計方法可行性進行了驗證研究.表2～4是應用仿真數據給出的3條車道通行能力分布估計結果.

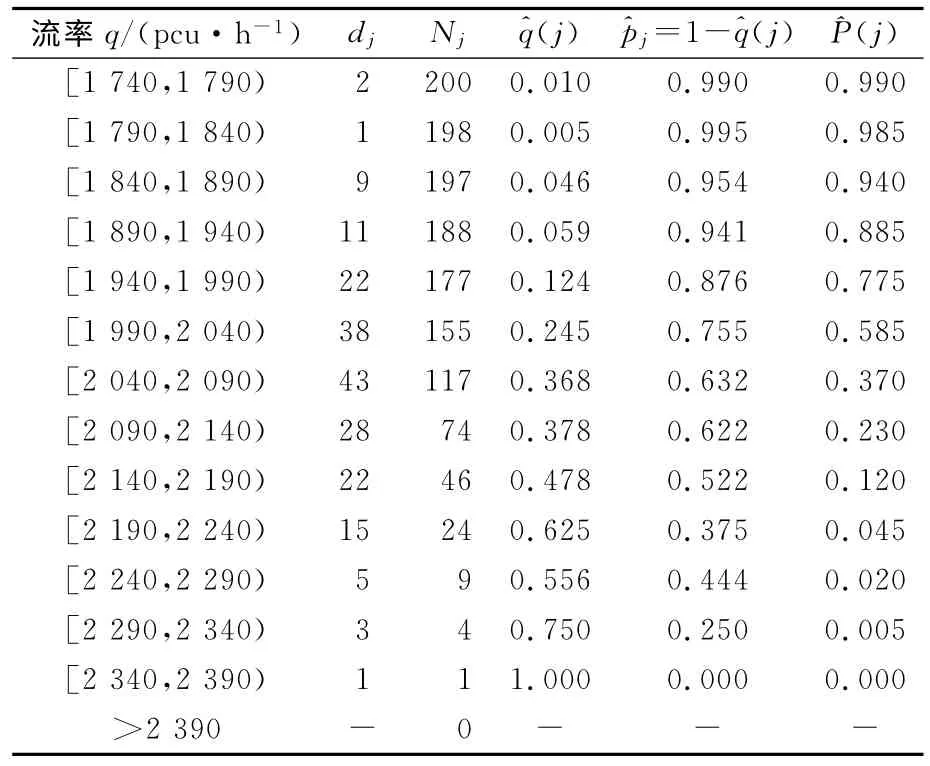
表2 第1車道通行能力分布估計結果

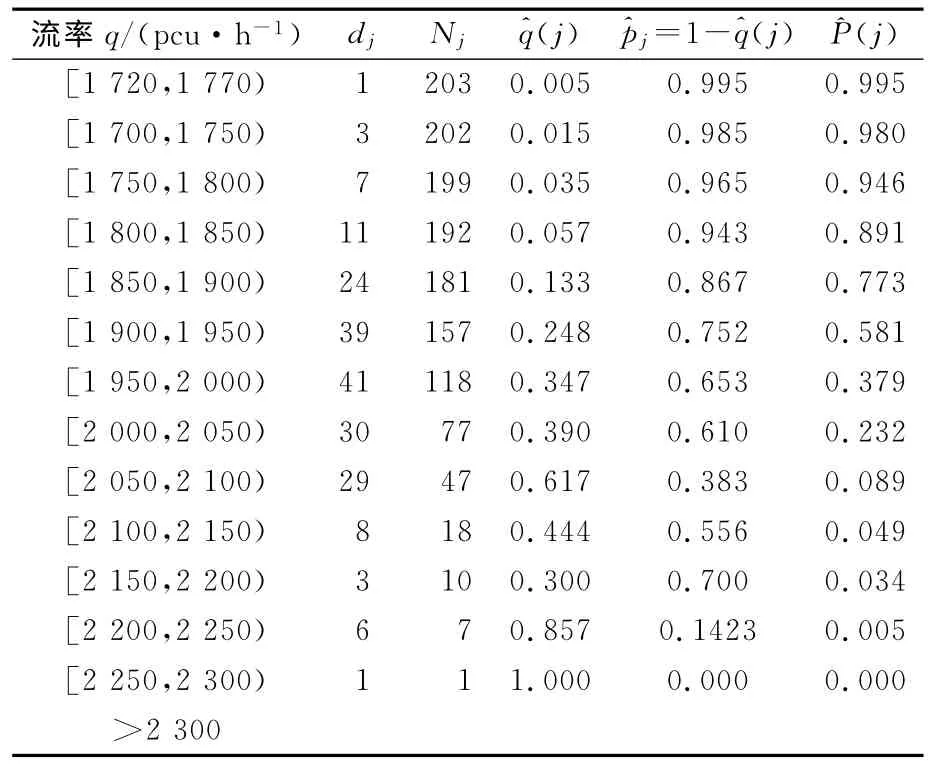
表3 第2車道通行能力分布估計結果

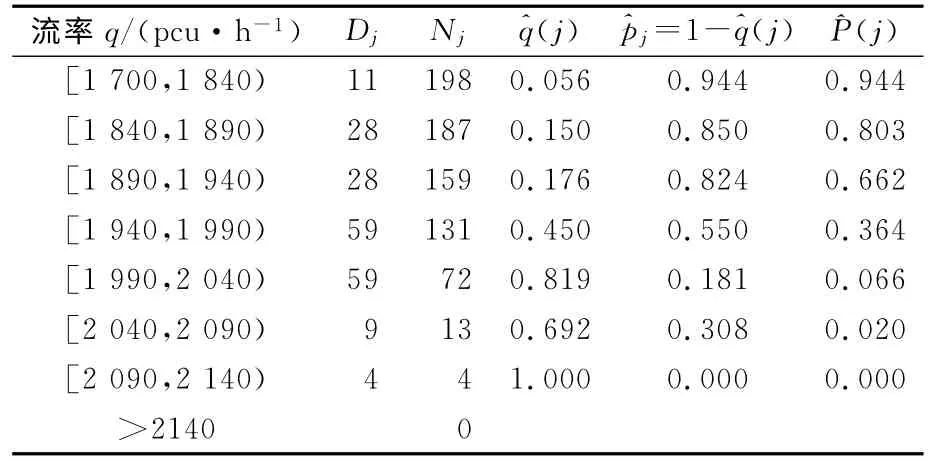
表4 第3車道通行能力分布估計結果

假設交通中斷概率20%所對應的流率為通行能力值（即當流率小于該通行能力值時，可以保證不發生交通中斷概率為），則由表2～4給出的結果可知，3 條車道的通行能力分別為1950，1870和1850pcu／（h·ln）.此外，應用傳統的通行能力計算方法，求得3條車道的通行能力值為分別為2060，2040和1990pcu／（h·ln），在上述交通流量水平下，不發生交通中斷的概率分別為0.37，0.23與0.36.

因此，基于交通中斷概率的通行能力分析方法和傳統通行能力分析方法相比，由于前者不僅考慮了道路設施適應的交通需求，還對設施運行可靠性進行了度量，更具有實用價值.

6 結束語

本文針對最新提出的“基于交通中斷概率分布的通行能力”定義，結合交通中斷特性和交通流觀測特點，給出了應用“乘積限方法”估計通行能力的方法和步驟.本次研究發現，盡管“基于交通中斷概率分布的通行能力”定義對道路設施交通運行評價和設計都具有較好的應用前途，但是其定義和估計方法存在許多的問題，如交通流統計時間間隔對該方法給出的估計結果精度的影響，交通流中斷判斷標準問題；此外，新的通行能力定義方法使得研究道路、交通等條件的影響難度增加.因此，在以后的研究中，需要對上述問題進一步分析.

［1］Transportation Research Board.Highway capacity manual［M］.Washington：National Research Council Washington，D.C.，2000.

［2］KERNER B S.Three－phase traffic theory and highway capacity［J］.Physics A：Statistical Mechanics and its Applications，2004（333）：379－400.

［3］邵長橋，榮 建，周 建.信號交叉口通行能力隨機性分析［J］.北京工業大學學報，2006，32（10）：919－21.

［4］TIAN Zong，MICHAEL K.New perspectives on the two－capacity phenomenon in freeway operations［CD］.Transportation Research Board 84thAnnual Meeting，National Research Council，Washington，D.C.，2005.

［5］MICHAEL K，MICHAEL D，PURUSHOTAM M B.Why field measurements differ from model estimates［J］.Transportation Research Record，2003（1852）：32－39.

［6］TARKO A，TIAN Zong.Example analysis and handling of uncertainty in the highway capacity manual with consideration of traffic diversion［J］.Transportation Research Record，2003（1852）：40－46.

［7］OZBAY K，EREN E O.A comparative methodology for estimating capacity of freeway section.Proceedings of the 2007IEEE［C］∥Intelligent Transportation System Conference，Seattle，WA，USA，Sept.30－Oct.3，2007.

［8］FRED L H，KWAKU A D.Freeway capacity drop and the definition of capacity［J］.Transportation Research Record，2003（1320）：91－97.

［9］LILY E，PONLATHEP L.Defining，measuring and estimating freeway capacity［C］∥Transportation Research Board 82nd Annual Meeting，National Research Council，Washington，D.C.，USA，2003.

［10］LAWLESS J F.壽命數據中的統計模型與方法［M］.茆詩松，濮曉龍，劉 忠，譯.北京：中國統計出版社，1998.