數字化配電網弧光接地故障的判斷

王曉芳，謝彥斌

(1. 邵陽學院 電氣工程系，湖南 邵陽，422000；2. 重慶大學 輸配電裝備及系統安全與新技術國家重點實驗室，重慶，400044)

數字化變電站的1個顯著特點是一次設備就地智能化[1]。這些智能設備中的微電子器件如數字輸出的電子式互感器中的A/D轉換器件抗電磁干擾及過電壓的能力十分弱。弧光接地是我國配電網常見的接地故障形式，弧光接地過電壓具有持續時間長，幅值較大的特點[2]，對數字化配網中的設備尤其是智能設備危害巨大，因此，抑制數字化配電網的弧光接地過電壓很有必要。目前，對弧光接地過電壓的預防最有效和最常用的措施是采用中性點經消弧線圈接地即諧振接地方式[2]。人工調諧的消弧線圈不僅不能及時準確投入補償，而且難以兼顧中性點電壓偏移的要求[3]，現已逐步淘汰。但自動調諧消弧線圈也有缺點，無論預調式還是隨調式，理論層面上還不完善，其補償并不區分單相接地故障類型，其中預調式還存在滅弧性能受到一定損失的缺陷[4]。對于電網中大量存在的自熄性電弧接地故障，不必要的操作不僅加劇了設備及電網所受的沖擊，而且不利于間隔較短的瞬時性接地故障的補償。對于永久性接地故障，不但不能消除故障,反而會給系統及設備帶來二次沖擊和大量諧波[5]。此外，消弧線圈的在線運行經驗顯示，預調式補償裝置存在阻尼電阻選擇困難、動作時間較長的固有缺陷，而隨調式動作雖快，但諧波污染嚴重[6]。鑒于補償裝置存在的上述種種問題，以及弧光接地過電壓產生的原因在于間歇性電弧接地[2]，謝彥斌[7]提出了正常運行時中性點絕緣運行、出現間歇性電弧接地故障時投入消弧線圈的運行策略。這種策略理論上不僅可以有效預防弧光接地過電壓的產生，而且可以避免消弧線圈大量不必要的操作以及補償裝置在線運行所帶來的諸多弊端。顯然，這種運行方式實現的基礎和關鍵在于對間歇性電弧接地故障進行及時準確的判斷。代姚[8]為此提出了比較詳細的運行控制策略，但其相關的接地判斷依賴于接地過渡電阻較小的情況，而實際上配電網單相接地故障多為中、高阻[9]。關于間歇性電弧接地故障的判斷，司馬文霞等[5]提出了基于 COOCG形態濾波的算法；Lorenc等[10]提出了基于小波分析的自適應算法；劉渝根等[11]則利用電弧重燃與熄滅的反復與間斷性提出了判據，但它們同樣是基于接地電阻較小的情況；Michalik等[12]也提出了基于小波分析的方法，但是算法比較復雜。為此，本文作者以35 kV電網為例對配網單相接地故障進行分析計算，得出臨界零序電壓的概念(即中性點不接地系統的單相接地故障電流為10 A時的零序電壓)及其可區分間歇性電弧和自熄性電弧接地故障的作用，并結合單相接地故障電流的動態特征得到間歇性電弧接地故障的判據。在此基礎上，再提出以僅在間歇性電弧接地時才投入補償為特點的數字化配電網弧光接地過電壓的預防策略。

1 臨界零序電壓概念的提出及其應用

1.1 臨界零序電壓概念的提出及其計算公式

本文以 35 kV電網為例(由于僅在間歇性電弧接地時投入補償，中性點正常運行時不接地)，說明臨界零序電壓的概念、作用及其計算式。

電弧接地故障是否消除及其弧光接地過電壓產生的物理機理皆在于電弧的重燃。影響電弧重燃的因素是多方面的，但當電弧電流低于10 A時[13]，電弧不會重燃，反之，則會重燃并形成間歇性電弧接地故障。標準DL/T 620—1997規定：當單相接地故障電容電流大于10 A(35 kV電網)時，中性點應采用經消弧線圈接地的方法。本文定義單相接地故障電流為10 A時對應的中性點電壓為臨界零序電壓，通過比較中性點電壓與臨界零序電壓的關系來反推接地故障電流是否大于 10 A，從而判斷間歇性電弧接地故障存在的可能性。下面對臨界零序電壓進行簡要推導。

35 kV電網單相接地等值接線圖如圖1所示。圖1中：Re和Ie分別為電弧性單相接地故障時的過渡電阻和接地電流；U0為系統零序電壓；Rs和Ls分別為線路等效損耗電阻和電感；ca，cb和cc分別為a相、b相和c相對地電容；RL和XL為負載阻抗；SW為模擬接地電弧熄燃的開關。

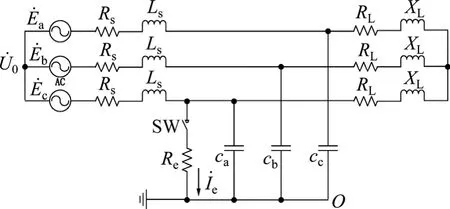
圖1 中性點絕緣時35 kV電網單相接地等值接線圖Fig.1 One-phase earthed equivalent circuit of 35 kV grid

假設輸電線路上各處電壓基本相等，且 Rs和 Ls的影響可忽略不計。由于零序電壓無法流過對稱負載，因而，對零序電壓進行分析時可近似認負載開路，由此可得：

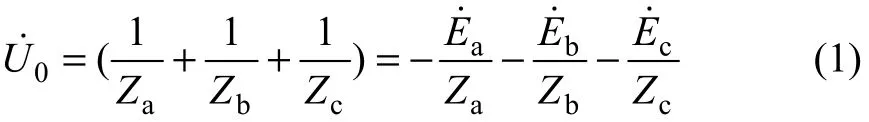
式中：

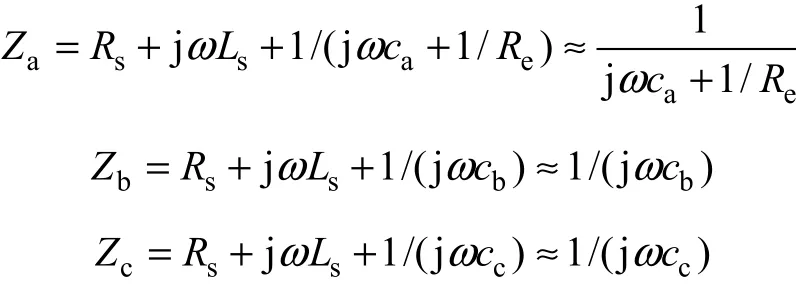
ca，cb和cc相差不超過10%，為了分析方便，令ca=cb=cc=c0，則化簡式(1)可得：

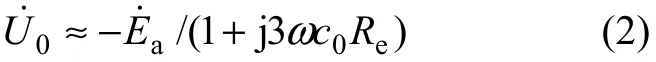
此時，有：

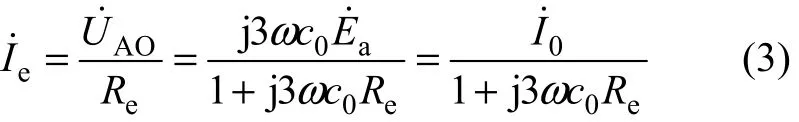
記相電壓為Uph，Ie為10 A時的零序電壓即臨界零序電壓為U0c，相應的臨界過渡電阻為Rec，則

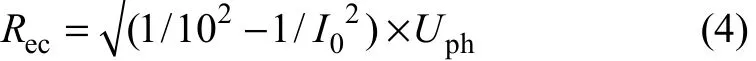
將式(4)代入式(2)得：

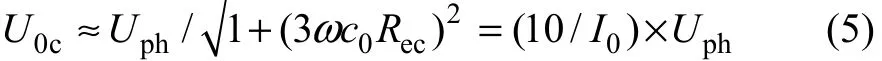
35 kV線路總存在一定的不對稱度。位置較高處的相(記為中相)對地電容較小，而處于邊緣或較低處的另兩相(記為邊相)對地電容稍大，這被現場實測結果所證實[7]。設 B 相為中相，則可設 Cb=C-Δc，Ca=Cc=C，Ca+Cb+Cc=3c0，結合不對稱度U00的計算式可得：

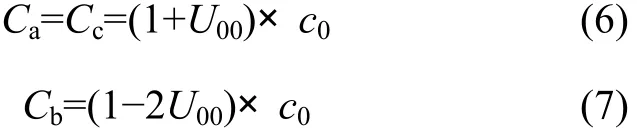
記邊相接地時的臨界零序電壓為U0c1，將式(4)～(7)及I0代入式(1)可得：

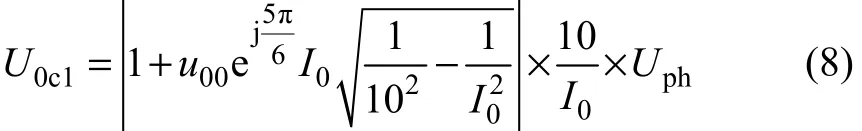
記中相接地時的臨界零序電壓為U0c2，則U0的表達式為

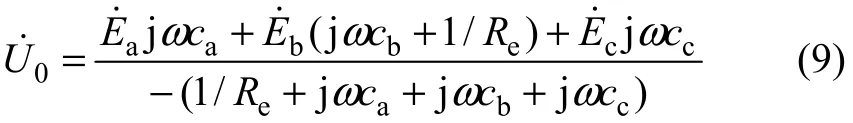
將式(4)～(7)及I0代入式(9)并化簡可得：

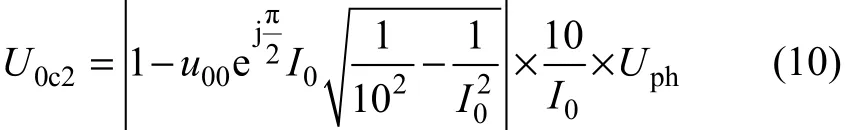
1.2 U0c1(或U0c2)在間歇性電弧接地判斷中的應用

由式(2)和(3)可知：零序電壓 U0與接地電流Ie的關系為U0≈(Uph/I0)×Ie，即U0與Ie為正比例關系。因此，對于電弧性接地，當 Ie＜10 A 時，U0＜U0c1(或U0c2)，電弧不會重燃，或逐漸自熄；反之，當Ie＞10 A時，U0＞U0c1(或U0c2)，電弧會間歇重燃。可見：對于電弧性接地故障，U0＞U0c1(或U0c2)可作為間歇性電弧接地故障的判斷標準。

由于 U0＞U0c1(或 U0c2)作為間歇性電弧接地故障判斷標準的前提是故障為電弧性接地，而配網中的單相接地故障包括永久性接地和電弧性接地(包括間歇性電弧接地和自熄性電弧接地)2種類型，所以，還需進一步分析這2種故障類型的區別。

2 電弧性接地故障與永久性接地故障的區別

下面通過電弧性與永久性單相接地故障的零序電流或故障相電流的特征來區分這2種故障。

2.1 2種故障的零序或故障相電流的特征區別

圖 2所示為文獻[12]提供的某配網電弧性接地故障時的實測零序電流波形。

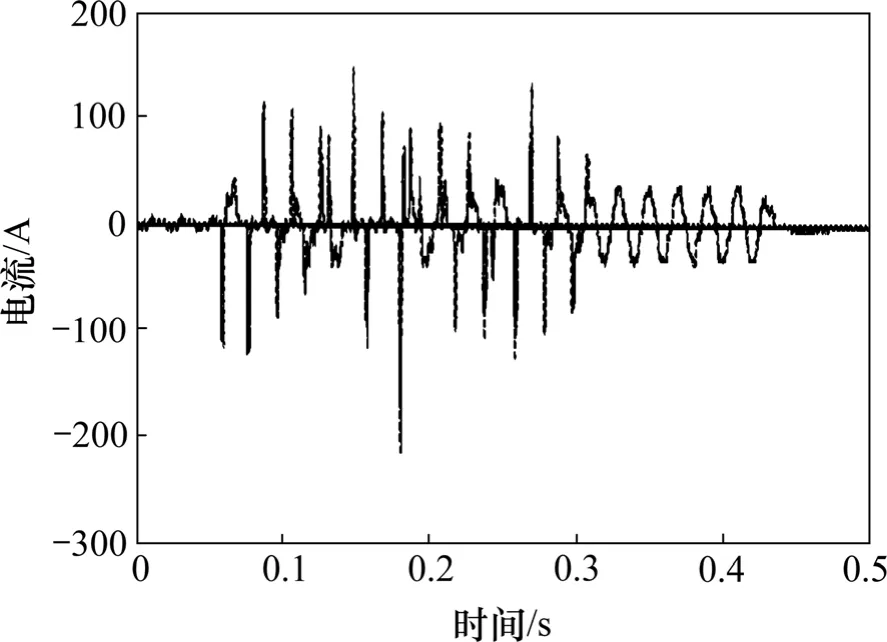
圖2 電弧性接地故障時的實測零序電流波形Fig.2 Neutral current wave of arcing fault in a distribution grid

由圖2可知：發生間歇性電弧接地故障時，電流幅值存在躍變現象。這種躍變是電弧熄滅與重燃引發的暫態高頻振蕩的結果。

實際上，當過渡電阻較高時可能沒有明顯的躍變現象，甚至電弧會逐漸自熄或不重燃，但由于存在零休，在電弧電流過零時刻附近會出現波形斜率變化較大的情況，如圖3中虛線圈內所示[14]。由于交流電弧的熱慣性，電弧電流過零后弧隙可能因未完全去游離而存在弧后電流，因此，零休附近的斜率變化不一定有圖3中那么明顯。

而對于永久性接地故障，其零序電流在穩態時基本為正弦波形，不存在躍變或斜率突變的現象。雖然故障初期存在一定的暫態高頻分量，但其振蕩頻率高達數百赫茲，衰減很快[15]。

綜上所述，電弧性接地故障相對于永久性接地故障的零序電流/故障相接地電流的特征區別為：(1)電流幅值存在躍變現象；(2)在電流過零時刻附近波形斜率變化較大。

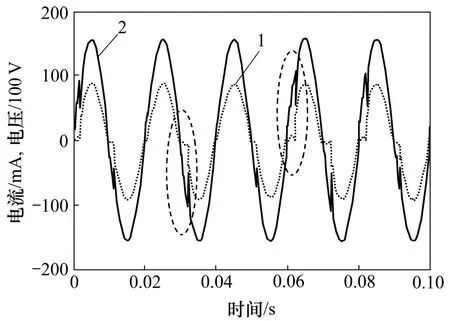
圖3 過渡電阻很高時的實測電弧接地電流波形Fig.3 Experimental current wave of arcing fault in MV network

若僅滿足第(1)條要求，則為自熄性電弧接地故障，僅滿足第(2)條要求則為永久性接地故障。

相對基于固定零序電壓閥值的補償策略，將 U0＞U0c1(或U0c2)作為判據的1個條件，既可以避免自熄性電弧接地故障的補償操作，又可以不漏掉間歇性電弧接地的補償，具體分析式(8)～(9)對應的U0c1(或U0c2)與I0的關系曲線見圖4。由圖4可知：對于I0小于某一水平(即紅線與曲線的交點對應的 I0)的配網，基于固定零序電壓閥值的補償將涵蓋自熄性電弧接地故障(U0＜U0c1(或U0c2))；而對于大于該水平的配網，一部分間歇性電弧接地故障將被漏掉。

2.2 電弧性接地與永久性接地故障的區分標準

為了反映電流躍變和電流波形斜率的變化，分別定義電流變化率 K=di/dt以及電流斜率變化率

對于電弧性接地故障，當電流過零時刻附近電流斜率變化較大時，設Krc為區別這2種故障的Kr閥值(本文取 Krc=1)，則有 Krmax＞Krc(其中，Krmax為 Kr的最大值)；當電流幅值存在躍變現象時，K趨于∞。設Kc為可區分這2種故障的閥值(本文取Kc=5×104)，則有Kmax＞Kc。

對于永久性接地故障，零序電流中的高頻暫態成分很快衰減，則剩下的穩態工頻成分在過零時刻附近時K很大但變化很小，因此，Kr≈0，Krmax＜Krc。另由式(3)可知：Kmax=2I0ω(其中，ω為角頻率)，則Kmax＜Kc。

綜上所述，這2種故障類型的區分標準為：Krmax＞Krc或Kmax＞Kc。滿足該標準的故障為電弧性接地故障，否則為永久性接地故障。

至于具體算法，鑒于永久性接地故障時高頻暫態成分衰減較快，可以適當延時后再進行計算。同時，為了增大檢驗的可靠性，可以在檢驗到2次以上Krmax＞Krc或Kmax＞Kc時再進行判斷。

3 間歇性電弧接地判據

綜上所述，間歇性電弧單相接地故障判據為：

(1) Krmax＞Krc(過零時刻附近)；(2) Kmax＞Kc，且U0＞U0c1(或 U0c2)。

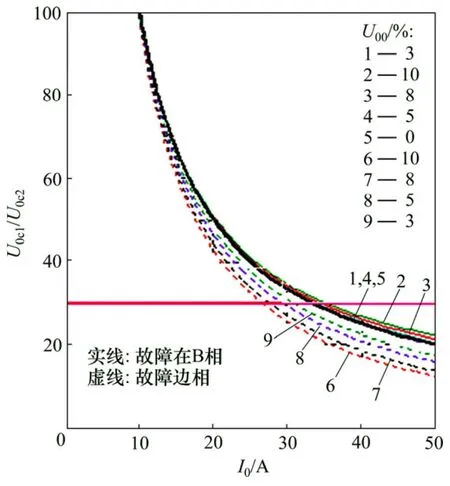
圖4 U0c1(或U0c2)與I0的關系曲線Fig.4 Relationship between U0c1( or U0c2) and I0

由于本文中 U0和 U0c1/U0c2都屬于穩態范疇，所以，還需分析其受暫態過程的影響及間歇性電弧接地判據的工程可行性。

4 判據的仿真測試

以圖1所示的35 kV電網為例進行仿真，A相接地。為了分析方便，忽略電網不對稱度，即 U00=0。仿真模型見文獻[7]，系統參數分別取為：c0=1.575 μF，Rs=9.5 Ω，Ls= 62 mH，Y 型負載 XL=1012Ω, cos φ=0.8。電弧的熄滅采用工頻熄弧理論，即工頻電流過零時熄滅。但重燃時刻并不是在下一個電壓峰值附近，而是零休后立即重燃。其原因是：一方面，按文獻[2]中的方法，電網中性點由于電荷累積而出現直流電位，但在實際工作中并沒有觀察到這種現象；另一方面，文獻[15]顯示，高阻性電弧接地故障時有明顯的零休現象。電弧的熄滅、零休與重燃通過電弧接地開關的開閉實現，零休時間參照文獻[15]取1 ms。

由式(3)可知：Ie與 Re負相關，即當 Re＜Rec時，有Ie＞10 A；反之，有Ie＜10 A。可見：Re在物理上可以決定電弧的熄燃與否。為此，本文通過調整 Re以及電弧接地開關的開閉，分別模擬間歇性電弧和自熄性電弧故障。永久性接地故障，通過永久閉合接地開關來模擬。仿真分4個案例，見表1。仿真結果如圖5～8所示，其中圖5～ 7所示的故障相電弧性接地電流波形與文獻[9]中的實測波形很相似，說明本仿真結果是可信的。

根據仿真波形數據可以計算有關判據的參數。對Kmax進行計算時，考慮到單相接地故障時暫態分量的頻率不超過3 kHz，取計算步長為0.01 ms。計算Krmax時，鑒于零休時間為1 ms，取計算步長為0.1 ms，并判斷所需的其他參數。由仿真條件知：U0c≈9.5 kV，Rec≈1.905 kΩ。參數計算及判斷結果見表1(符號“—”表示無需計算)。

表1 參數計算及判斷結果統計Table 1 Results of parameter calculations and judgement

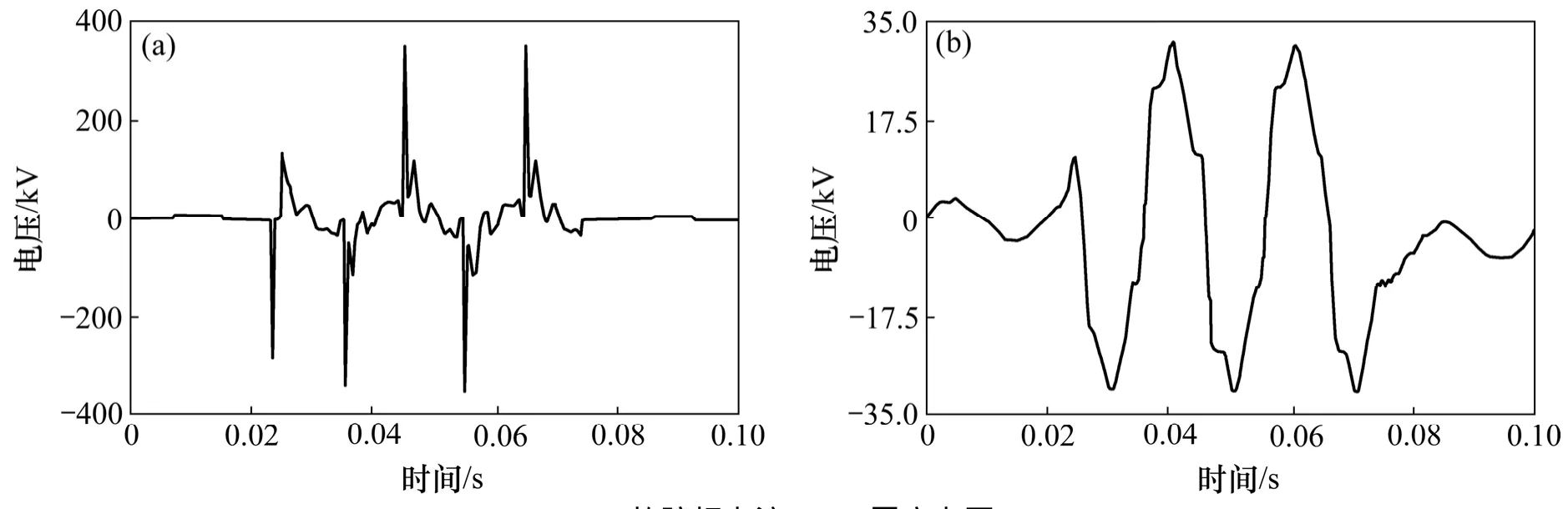
圖5 案例1：電弧電阻為40 Ω時的仿真波形Fig.5 Waveforms of case 1 (arcing fault is 40 Ω)

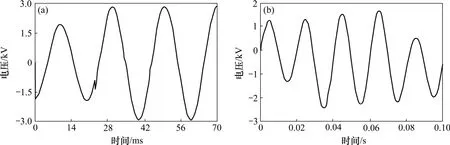
圖6 案例2：電弧電阻為10 kΩ時的仿真波形Fig.6 Waveforms of case 2 (arcing fault is 10 kΩ)

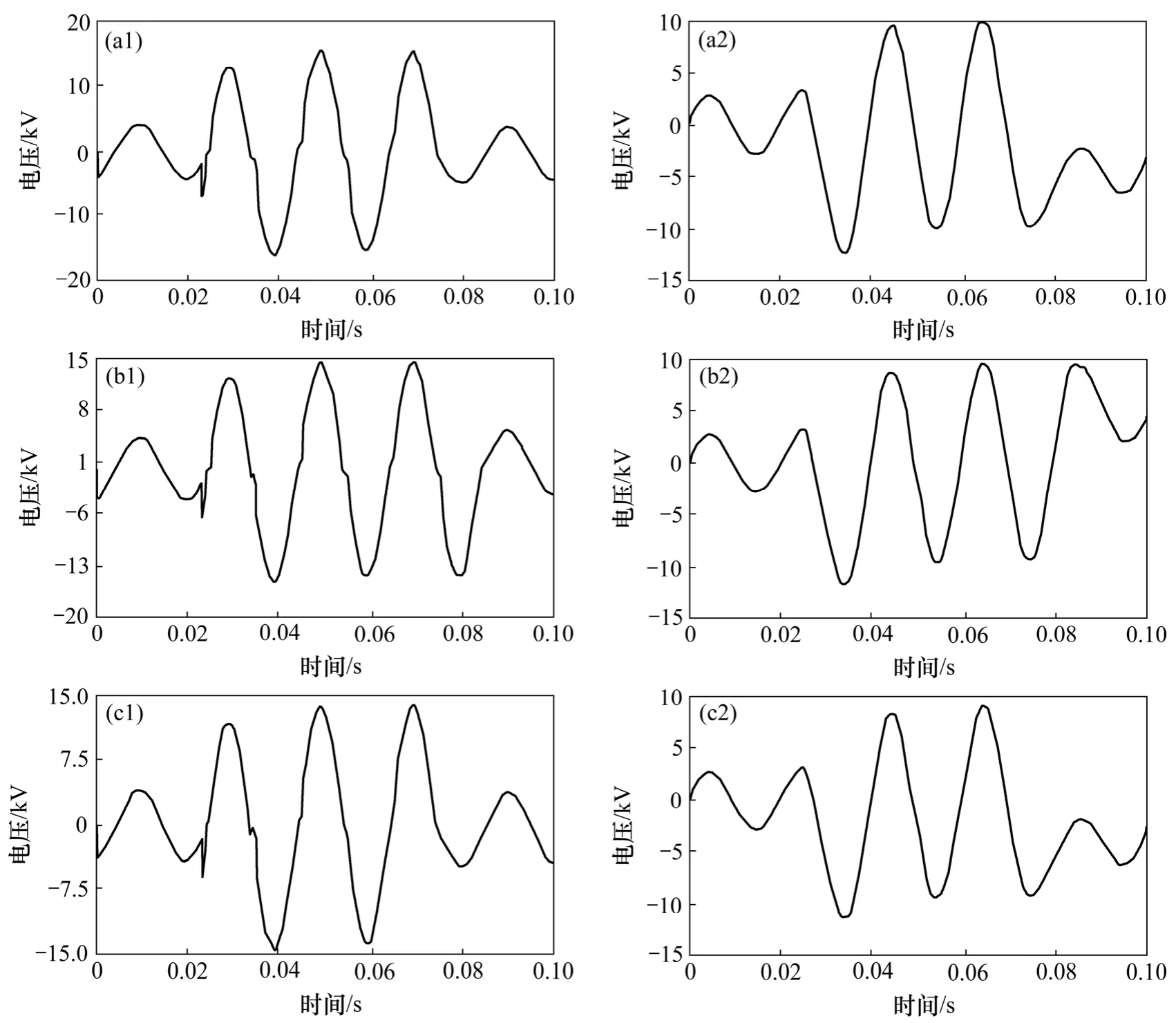
圖7 案例3：電弧電阻不同時的仿真波形Fig.7 Waveforms of case 3 at different arcing faults

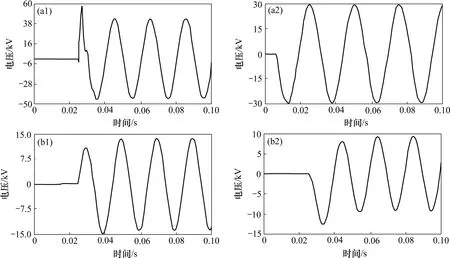
圖8 案例4：電弧電阻不同時的仿真波形Fig.8 Waveforms of case 4 at different arcing faults

表中案例3的目的是考察Re≈Rec或Ie≈10 A時判據的有效性。由表 1 可知：無論是 Re＜＜ Rec，Re＞＞ Rec，還是Re≈Rec或Ie≈10A，判斷結果都是正確的。此外，由圖5～8可知：當Re較大時暫態過程不明顯，工程上有利于檢測，而 Re＜＜Rec時暫態振蕩非常劇烈，但此時U0＞＞ U0c，所以，并不影響判據的正確性，可見本判據準確可靠。

5 結論

(1) 零序電壓的作用以及故障電流的動態特征提出的間歇性電弧接地故障判據對高、低過渡電阻都適用。但判據算法還有待在實踐中不斷完善。

(2) 基于該判據的消弧線圈補償策略可以有效預防數字化配網弧光接地過電壓的產生。其特點是僅在間歇性電弧接地故障時啟動補償。

[1] 龐紅梅, 李淮海, 張志鑫, 等. 110 kV智能變電站技術研究狀況[J]. 電力系統保護與控制, 2010, 38(6): 146-150.PANG Hongmei, LI Huaihai, ZHANG Zhixin, et al. Research situation of 110 kV smart substation technology[J]. Power System Protection and Control, 2010, 38(6): 146-150.

[2] 張緯鈸, 何金良, 高玉明. 過電壓防護及絕緣配合[M]. 北京:清華大學出版社, 2002: 1-40.ZHANG Weibo, HE Jinliang, GAO Yuming. Overvoltage protection and insulation coordination[M]. Beijing: Tsinghua University Press, 2002: 1-40.

[3] 劉渝根, 丁伯劍, 袁濤. 山區35 kV電網中性點新型運行方式研究[J]. 高電壓技術, 2006, 32(1): 32-34.LIU Yugen, DING Bojian, YUAN Tao. New neutral point operation method of 35 kV grids in mountainous area[J]. High Voltage Engineering, 2006, 32(1): 32-34.

[4] 韓靜, 徐麗杰. 中性點經消弧線圈瞬時并聯小電阻接地研究[J]. 高電壓技術, 2005, 31(1): 38-39, 52.HAN Jing, XU Lijie. Study of a neutral grounding method with an arc suppression coil and a parallel low resistance[J]. High Voltage Engineering, 2005, 31(1): 38-39, 52.

[5] 司馬文霞, 冉銳, 袁濤. 采用數學形態學的弧光接地過電壓識別方法[J]. 高電壓技術, 2010, 36(4): 835-840.SIMA Wenxia, RAN Rui, YUAN Tao. Identification of arc grounding over-voltage using mathematical morpholog y transform[J]. High Voltage Engineering, 2010, 36(4): 835-840.

[6] 李云飛. 預調式消弧線圈導致系統不平衡加劇的原因分析[J].水電能源科學, 2008, 26(2): 175-177.LI Yunfei. Analysis of cause for aggravation of primary system after arc-suppression coil connected[J]. Water Resources and Power, 2008, 26(2): 175-177.

[7] 謝彥斌. 山區35 kV電網中性點新型運行方式研究[D]. 重慶:重慶大學電氣工程學院, 2008: 10, 34.XIE Yanbin. A new neutral operation mode of 35 kV grid in mountainous area[D]. Chongqing: Chongqing University.College of Electrical Engineering, 2008: 10, 34.

[8] 代姚. 配電網鐵磁諧振及弧光接地過電壓特征識別與抑制方法[D]. 重慶: 重慶大學電氣工程學院, 2010: 65-66.DAI Yao. Recognition and suppression methods for ferroresonance and grounding arc over-voltage in distribution power system[D]. Chongqing: Chongqing University. College of Electrical Engineering, 2010: 65-66.

[9] H?nninen S, Lehtonen M. Characteristics of earth faults in electrical distribution networks with high impedance earthing[J].Electric Power Systems Research, 1998, 44: 155-161.

[10] Lorenc J, Musierowicz K, Kwapisz A. Detection of the intermittent earth faults in compensated MV network[C]//2003 IEEE Bologna Power Tech Conference. Bologna, Italy, 2003:496-501.

[11] 劉渝根, 謝彥斌. 山區 35 kV電網單相接地故障類型判斷方法[J]. 高壓電器, 2009, 45(4): 103-105.LIU Yugen, XIE Yanbin. Judgement method on single phase-to-ground fault type of 35 kV grids in mountainous area[J].High Voltage Apparatus, 2009, 45(4): 103-105.

[12] Michalik M, Rebizant W, Lukowicz M, et al. Wavelet transform approach to high impedance fault detection in mv networks[C]//2005 IEEE Power Tech. Russia, 2005: 1-7.

[13] 顏湘蓮, 陳維江, 賀子鳴, 等. 10 kV配電網單相接地故障電弧自熄特性的試驗研究[J]. 電網技術, 2008, 32(8): 25-18, 34.YAN Xianglian, CHEN Weijiang, HE Ziming, et al.Experimental research on self-extinction behavior of arc caused by single-phase earth fault in 10 kV distribution network[J].Power System Technology, 2008, 32(8): 25-18, 34.

[14] Elkalashy N I, Lehtonen M. Modeling and experimental verification of high impedance arcing fault in medium voltage networks[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(2).

[15] 王智, 汪芳宗. 配電系統接地故障檢測的一種新算法[J]. 電力系統保護與控制, 2011, 39(20): 48-51.WANG Zhi, WANG Fangzong. A new method of earth fault detection in distribution system[J]. Power System Protection and Control, 2011, 39(20): 48-51.